形狀記憶合金梁在簡諧和白噪聲聯(lián)合激勵下的混沌及安全盆侵蝕現(xiàn)象

葛 根，竺致文，許 佳

(1.天津工業(yè)大學 機械工程學院，天津 300160;2.天津大學 機械學院工程力學系，天津 300072)

形狀記憶合金梁的振動具有豐富的非線性動力學特性，研究其振動特性對研究形狀記憶合金的工程應用具有重要的實用價值。比如，微型泵的形狀記憶合金隔膜和形狀記憶合金機械夾的振動，可當做形狀記憶合金梁模型來處理。

目前對形狀記憶合金的本構模型研究眾多[1－7]，這些研究主要集中在熱動力學理論，微觀力學理論，相變理論等領域，而且這些本構模型的數(shù)學表達式多為符號函數(shù)或分段函數(shù)。因此基于這些模型的形狀記憶合金構件的振動分析變得較為困難，從而學者們傾向于數(shù)值模擬多于理論分析。國內外學者近年來提出了眾多關于形狀記憶合金梁振動的研究成果。Collet等[8]在考慮了SMA的在拉、壓和溫度載荷中的對稱性假設后，研究了形狀記憶合金梁的動力學行為。Hashemi等[9]研究了在拉、壓和溫度加載中的非對稱性假設下梁的自由振動和脈沖激勵振動問題。Marcclo等[10]用數(shù)值方法研究了形狀記憶合金雙桿系統(tǒng)的同宿分岔和混沌現(xiàn)象。張清泉等[11－12]根據(jù)Machado本構模型建立了形狀記憶合金梁的動力學模型并研究了其振動的穩(wěn)定性和混沌現(xiàn)象。吳志強等[13]研究了形狀記憶合金層合梁的非線性動力響應特性。葛根等[14]研究了簡支形狀記憶合金梁受簡諧激勵下的混沌閾值問題。這些研究集中在確定性系統(tǒng)范圍內，而都沒有研究隨機激勵對系統(tǒng)發(fā)生混沌的影響及激勵幅值對系統(tǒng)安全盆的邊界的侵蝕現(xiàn)象。

本文基于van-der-pol環(huán)模型模擬了形狀記憶合金本構模型中的遲滯環(huán)特性。該模型為光滑函數(shù)，從而有利于理論分析。從該模型出發(fā)建立了受軸向簡諧、橫向白噪聲聯(lián)合激勵下的形狀記憶合金簡支梁的振動模型。利用隨機Melnikov過程法得出系統(tǒng)發(fā)生隨機混沌的閾值必要條件。為了充分說明系統(tǒng)是否發(fā)生混沌，采用數(shù)值方法得到了系統(tǒng)安全域邊界的侵蝕現(xiàn)象，發(fā)現(xiàn)激勵幅值的變化導致安全盆內部出現(xiàn)分形結構，這是識別混沌的另一種有效而可靠的方法。這些結果對SMA梁的應用安全具有較大的實際意義。

1 形狀記憶合金梁的振動模型

考慮一個矩形截面的簡支Euler-Bernoulli形狀記憶合金梁如圖1所示。梁長為l，b為橫截面寬度，h為梁高。中點的y方向位移為w。軸向受簡諧激勵N，形式為:N=p0+pcos(Ωt)，同時受施加在梁中點的面內橫向隨機激勵Fη(t)，F(xiàn)為幅值，η(t)為標準高斯白噪聲，具有零均值，強度為D。

因為形狀記憶合金滿足拉壓條件下的應力應變關系的對稱性[8]，故坐標中心可取為梁橫截面的幾何中心處。

圖1 簡支形狀記憶合金梁的模型及坐標Fig.1 The model and the coordinate of the simply supported SMA beam

假設該梁為小撓度梁，其動力學方程為:

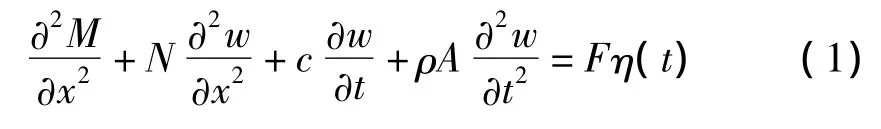
其中:c表示線性阻尼，ρ表示梁的密度，A為梁的橫截面積，M為梁的彎矩，w為中點橫向位移，該兩端簡支梁的邊界條件可表示為:

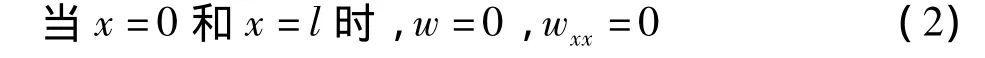
滿足振動邊界條件的一階模態(tài)為:

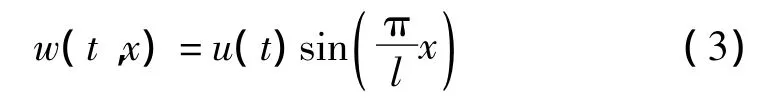
考慮小撓度梁的幾何變形條件:

可得彎矩的表達式為:

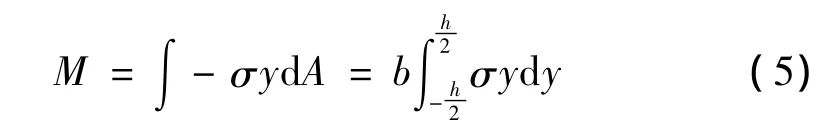
根據(jù)文獻[8]中的等應變加、卸載實驗數(shù)據(jù)可知，在不考慮溫度變化時，形狀記憶合金的加載－卸載應力應變曲線有明顯的滯后環(huán)特性。為模擬這一特性并使函數(shù)形狀光滑以利于后續(xù)分析，可考慮建立一個由關于原點對稱的vanderpol環(huán)加上一條骨架曲線形式的模型。

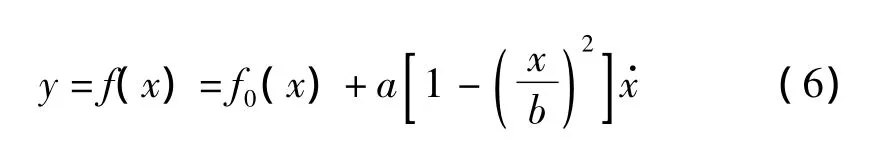
其中:f0(x)為遲滯環(huán)的骨架曲線;參數(shù)a，b表示骨架曲線和實驗應力應變曲線之間的偏差。假設應力－應變環(huán)的對稱中心為G(ε0，σ0)，則SMA的應力－應變關系可表示為:

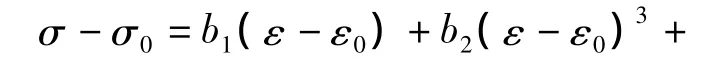
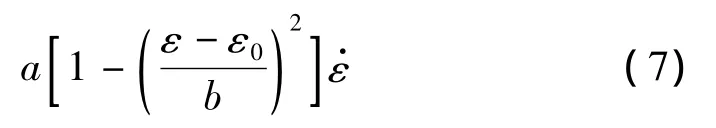
可展開為:

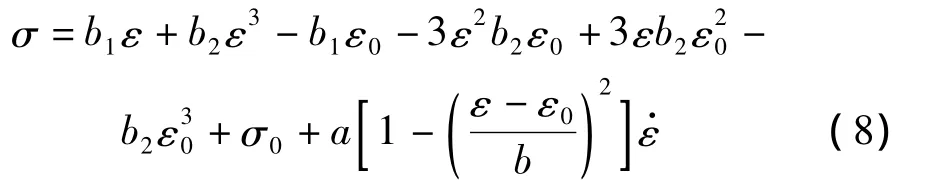
考慮到當ε=0時，加載和卸載曲線的對應應力值必需相等，且此時SMA應沒有殘余應力，故模型參數(shù)應滿足由此可得形狀記憶合金的應力應變最終函數(shù)關系為:

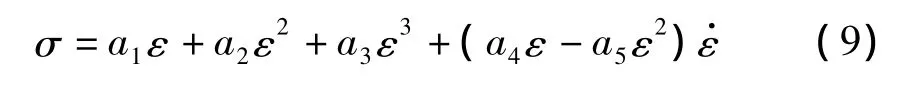
其中:

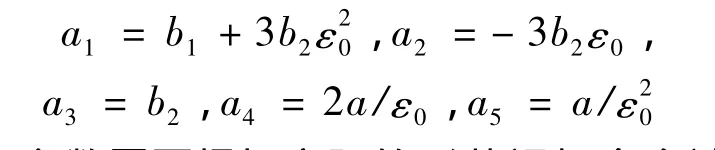
以上參數(shù)需要根據(jù)實際的形狀記憶合金試件的實測數(shù)據(jù)來確定。

把式(3)、(4)代入式(9)可得應力和位移w的關系后，再代入式(5)得彎矩表達式:

其中:I1=bh3/(12l2)，I3=bh5/80l6。

把式(3)、(10)代入式(1)并積分可得單自由度常微分形式的梁動力學非線性振動方程如下:

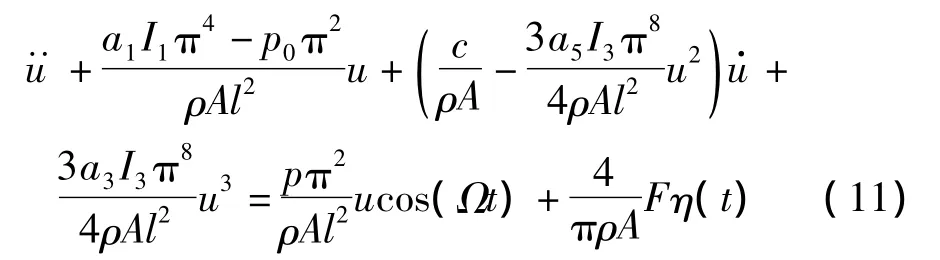
為了便于后續(xù)的非線性分析和揭示更豐富的系統(tǒng)可能存在的動力學現(xiàn)象，對式(11)作如下無量綱變化:并略去上標:

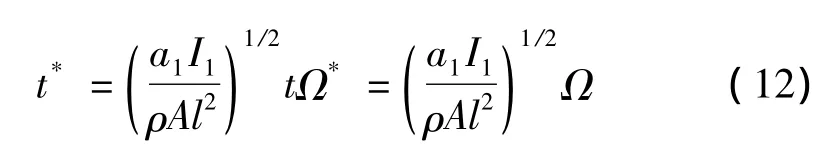
模型(11)可變形為如下無量綱形式:

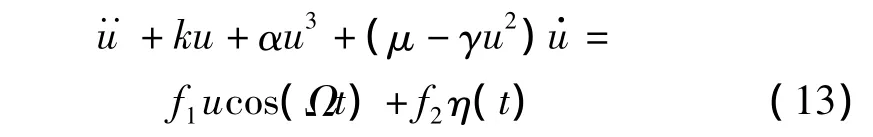
其中參數(shù)為:

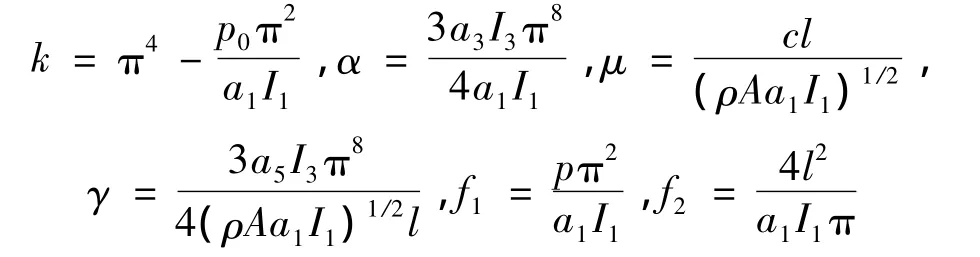
本文中考慮靜態(tài)載荷p0大于極限屈曲載荷，即線性剛度k為負(屈曲)的情況。對模型(13)引入如下尺度變換:可得:

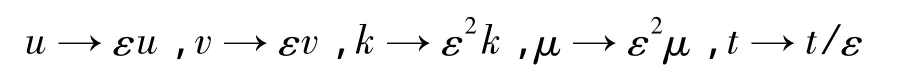
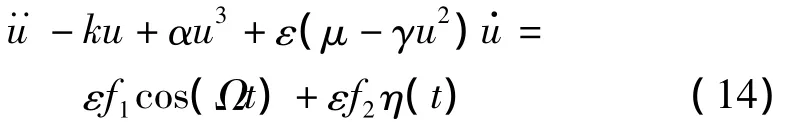
2 均方意義下Melnikov過程

根據(jù)文獻[15]，一個受弱噪聲激勵的弱阻尼單自由度Hamilton系統(tǒng)可表示為:

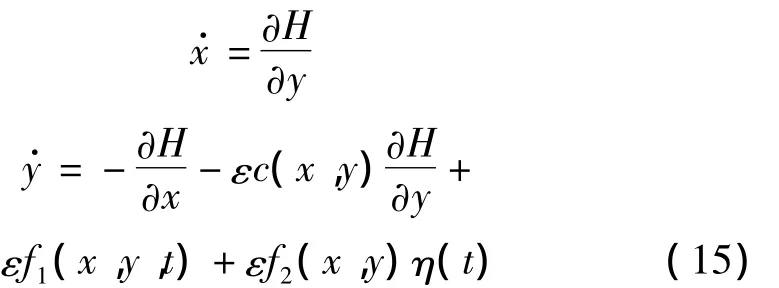
其中:x，y為廣義位移和廣義動量，H為廣義能量，c(x，y)為阻尼項，f1(x，y，t)為確定性激勵項，f2(x，y)為隨機激勵項系數(shù)，η(t)為白噪聲信號。

Melnikov方法是一種通過判斷系統(tǒng)的穩(wěn)定流形和不穩(wěn)定流形距離為零來判斷混沌的有效方法，它要求系統(tǒng)的激勵為連續(xù)且有界。由于η(t)對任意時間t1和 t2，取任意常數(shù) δ1＞0，令|η(t1)－ η(t2)|＜ δ1，則必存在一個常數(shù)δ2＞0使|t1－t2|＜δ2存在。由此可近似認為η(t)是連續(xù)且有界的，所以滿足Melnikov方法適用的前提假設。

根據(jù)Wiggins[16]提出的系統(tǒng)隨機Melnikov過程可表示為:

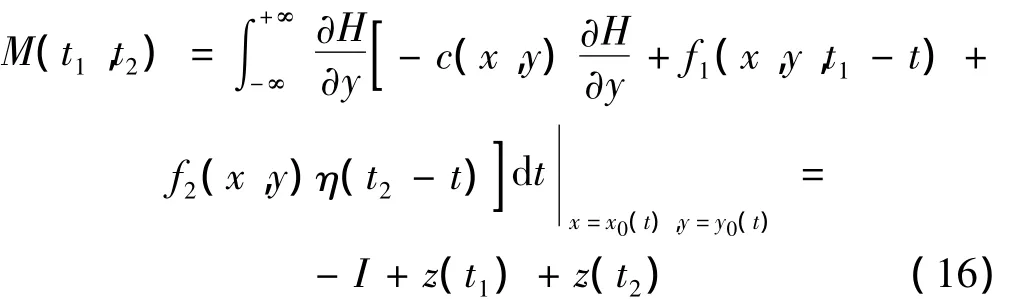
其中:x0(t)，y0(t)為系統(tǒng)(15)未擾時的同宿軌道表達式。

積分中的前兩項－I和z(t1)分別為阻尼項和確定性激勵項的隨機Melnikov積分的均值，第三項z(t2)表示由于隨機項引起的Melnikov過程積分。

把系統(tǒng)(14)式可變形為式(15)的形式，以便于后續(xù)處理。式(14)的系統(tǒng)Hamilton函數(shù)(廣義能量)為:，代入式(15)得:

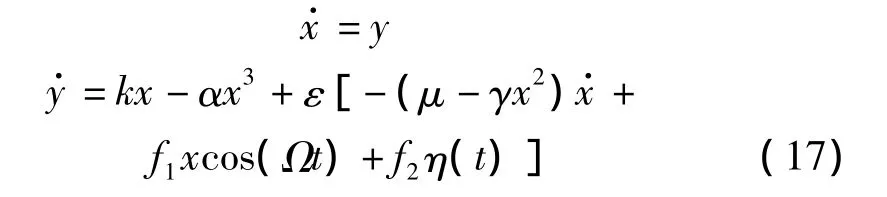
顯然系統(tǒng)(17)的未受擾系統(tǒng)存在鞍點(0，0)，從鞍點出發(fā)圍繞兩個中心的系統(tǒng)的同宿軌道Γ0(t)={Γ0－(t)|·|t∈R}可表示為:把式(18)，式(19)代入式(16)可得系統(tǒng)確定性部分的Melnikov積分表達式為:

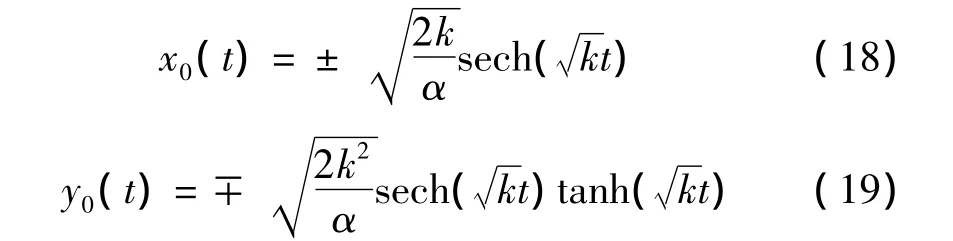
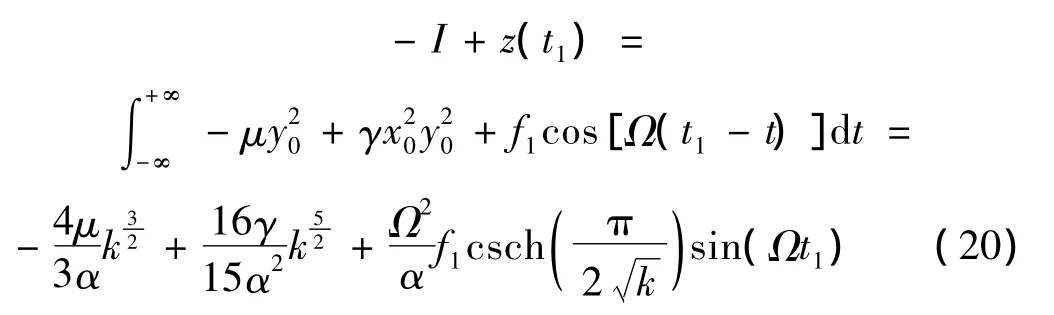
為便于計算式(16)中的z(t2)，可認為:

z(t2)=是系統(tǒng)隨機輸入η(t)通過一個線性濾波器后的脈沖響應函數(shù)，其傅里葉變換為:

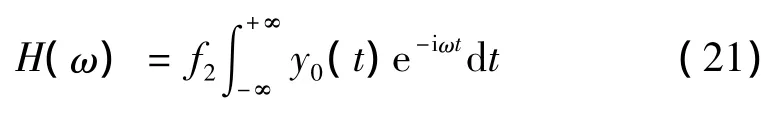
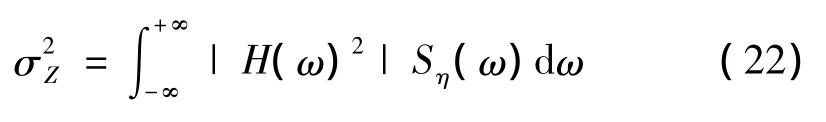
其中:Sη(ω)為白噪聲的譜密度。對白噪聲而言，譜密度為一個常數(shù)

從能量的角度[17]如此可得均方意義上系統(tǒng)可能發(fā)生隨機混沌的判據(jù)為:

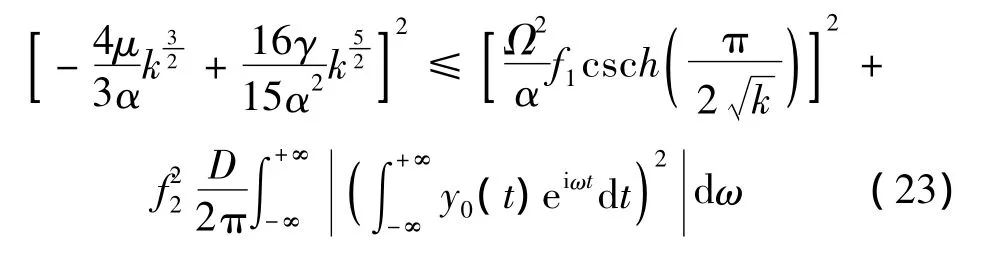
本文中取參數(shù)值為:

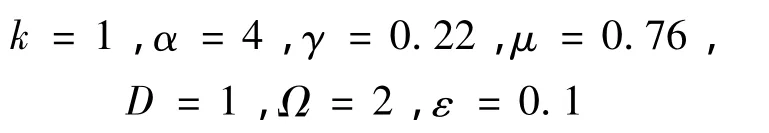
代入式(20)、(21)可得:

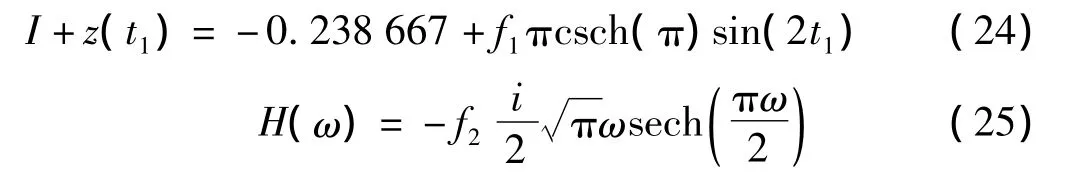
把式(25)代入式(23)后數(shù)值積分，可得:

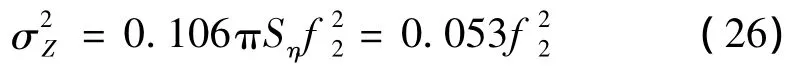
則滿足式(23)的激勵幅值f1，f2條件為:

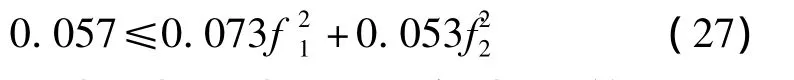
不等式(23)是發(fā)生隨機混沌的必要條件，但并不是發(fā)生隨機混沌的充分條件。下面內容將通過研究系統(tǒng)安全盆的分形現(xiàn)象來判斷系統(tǒng)混沌。

3 隨機安全盆的侵蝕現(xiàn)象

系統(tǒng)發(fā)生混沌時，穩(wěn)定流形和不穩(wěn)定流形將發(fā)生橫截相交，在相平面內盤旋纏繞成復雜結構，某些初始點出發(fā)的相軌線將穿出系統(tǒng)的安全域邊界，從而導致系統(tǒng)的不安全，這種現(xiàn)象在很多文獻中稱為安全盆的侵蝕現(xiàn)象。很多時候系統(tǒng)的安全盆受到侵蝕時，相軌線不斷逃逸出安全盆，并再回到安全盆內，因此安全盆邊界將呈現(xiàn)分形形狀，而安全盆的分形邊界是產(chǎn)生混沌的一個重要判據(jù)[18]。

為了研究系統(tǒng)的激勵對安全盆的影響，首先在相平面內描繪一個包含未擾系統(tǒng)安全盆的區(qū)域G。

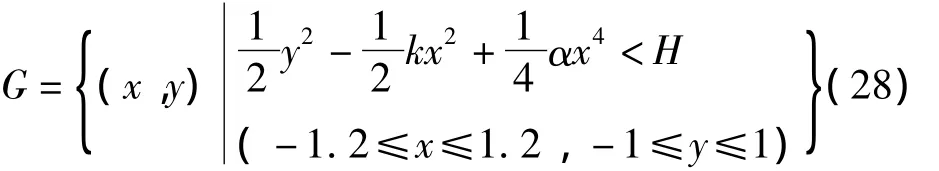
其中:H為系統(tǒng)的總能量上限，取H=0.1(圖2)。把區(qū)域G劃分為步長h=0.002的小格子，把每個小格子作為系統(tǒng)的初值，當某個初值在時間步長為0.01，迭代計算2×105次后仍然留在安全盆內，可認為該初值是安全的。隨機輸入采用蒙特拉羅法模擬，依次使用12組不同的白噪聲，只有當該初值在全部12組白噪聲激勵下都是安全的，才能記錄這個初值點，否則認為該初值是不安全的，在安全盆中刪除。

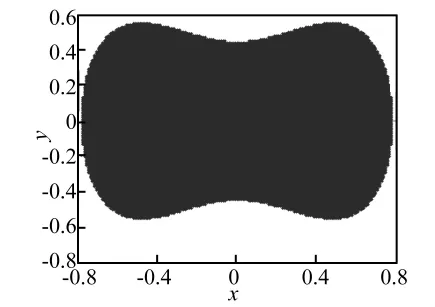
圖2 無擾系統(tǒng)的安全盆(H=0.1)Fig.2 The safe basin of the system(H=0.1)

當先不加隨機激勵時，增大確定性激勵幅值，觀察系統(tǒng)安全盆的形狀變化如圖3所示。

圖3(a)顯示，隨著確定性激勵滿足混沌判據(jù)(27)式，使系統(tǒng)的發(fā)生混沌，系統(tǒng)安全盆的邊界受到侵蝕，隨著激勵幅值f1增大，系統(tǒng)安全盆的內部出現(xiàn)分形的情況更明顯，如圖3(b)顯示。安全盆的內核部分(未擾系統(tǒng)的兩個中心附近)仍然是絕對安全的，而外圍部分區(qū)域就不能保證絕對安全。如圖3(c)顯示，即使系統(tǒng)在隨機外激勵作用下顯示出振動的隨機性，但是并沒有激發(fā)出系統(tǒng)內在的隨機行為(混沌)，則安全域的邊界仍為光滑的。

當隨機信號和簡諧激勵聯(lián)合作用后，仍取滿足式(27)的激勵幅值f2，安全盆的侵蝕情況如圖4所示。

比較圖3(a)和圖4(a)可知，隨機信號的加入使安全盆內部的安全點減少了，原來的平滑邊界也出現(xiàn)了分形。圖4(a)和圖4(b)的比較可知，加入的隨機激勵幅值變大后，安全盆內核部分的安全性變化不大，但是外圍區(qū)域的層狀分形結構變得十分明顯。而比較圖3(b)和圖4(c)可知，確定性激勵較大時，隨著隨機激勵的加入，安全盆內核安全區(qū)域仍幾乎不變，但是原來圖3(b)中的外層分形區(qū)幾乎全部消失。這一現(xiàn)象對SMA梁結構的實際應用具有一定的理論指導意義，實際的SMA梁的尺度一般較小，那么結構受到環(huán)境隨機干擾(熱噪聲，電磁噪聲)的影響就不能被忽略，為了使振動系統(tǒng)能夠“健康”地工作，在選擇系統(tǒng)的“初態(tài)”時應該只能選定為圖4(c)中的區(qū)域。圖4(c)和圖4(d)的比較可知，隨著隨機激勵幅值的進一步增大，安全盆的內核部分也逐步開始被侵蝕，分形結構逐步變得明顯。

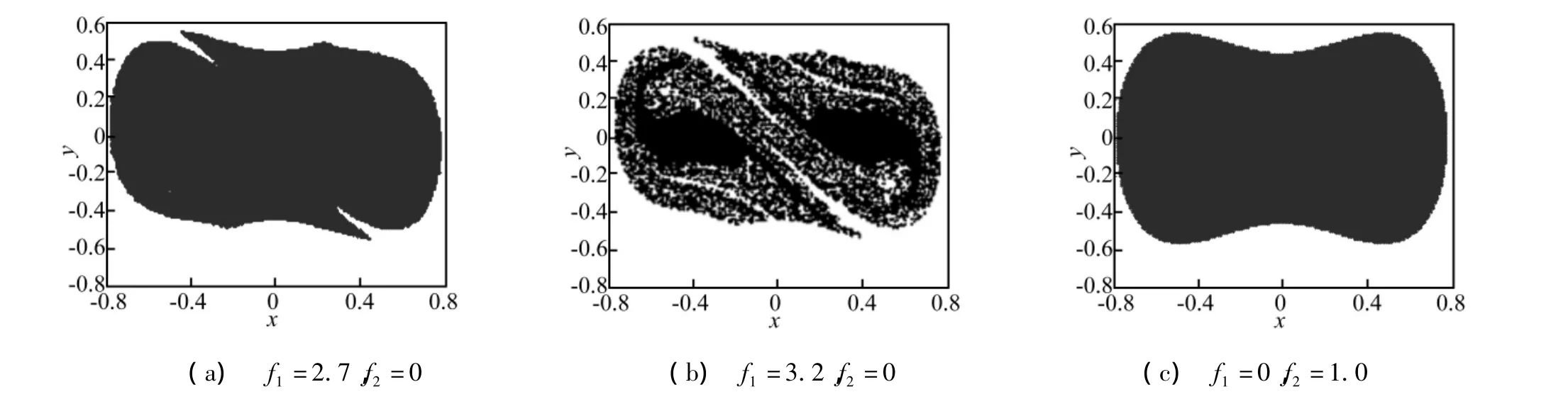
圖3 簡諧激勵或噪聲激勵下的安全盆Fig.3 The safe basin of the system under harmonic excitation or noise excitation

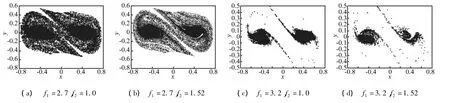
圖4 同時受簡諧和白噪聲聯(lián)合激勵時的安全盆Fig.4 The safe basin of the system under both harmonic and white noise excitations

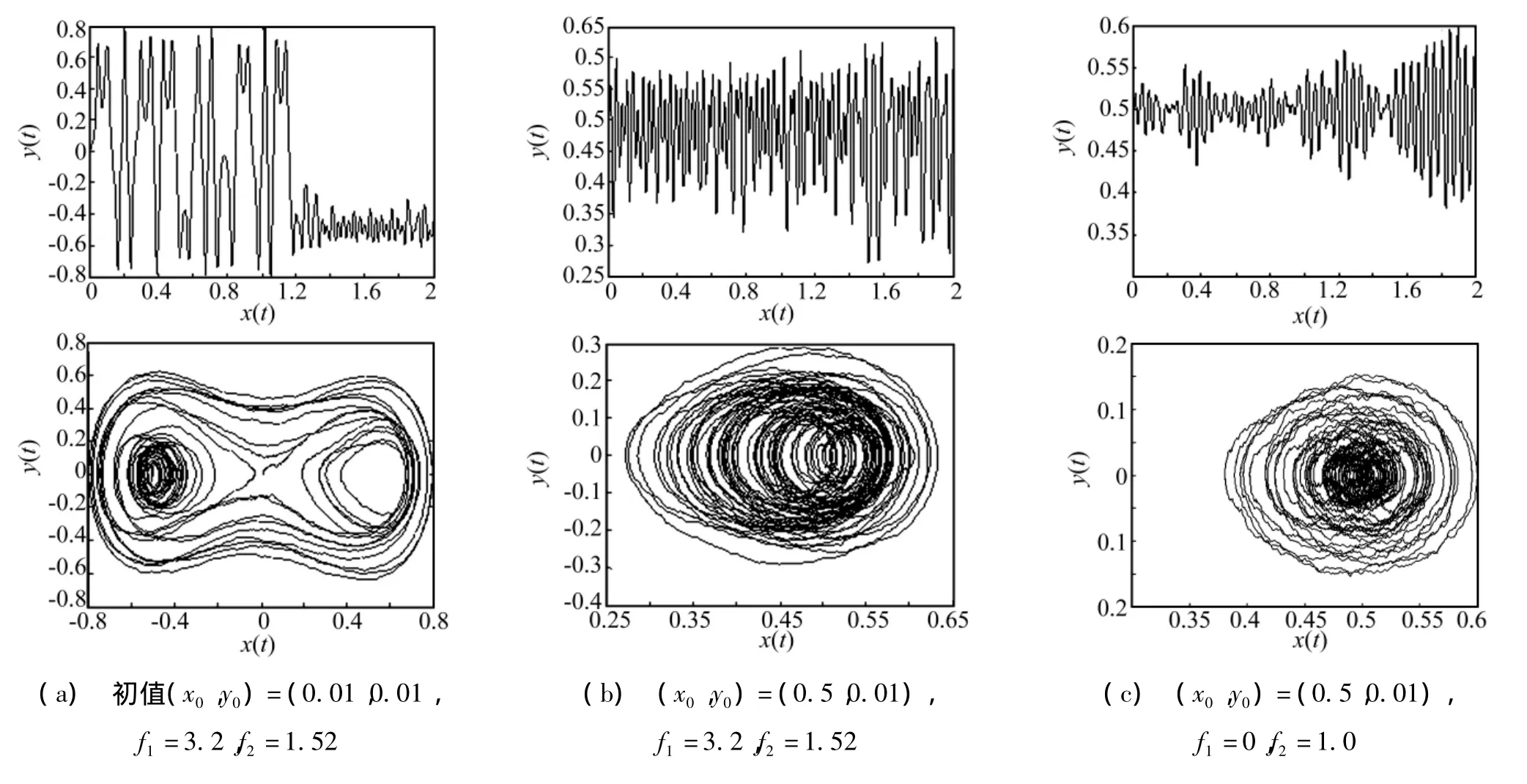
圖5 時間歷程和相圖Fig.5 Time series and phase portrait

混沌的一個典型特征是對初值的極端敏感依賴，為了進一步說明安全盆的侵蝕現(xiàn)象，觀察不同的初值點所形成的時間歷程和相圖如圖5所示。

圖5(a)顯示系統(tǒng)做混沌運動，圖5(b)顯示一種概周期運動，圖5(c)顯示的是在隨機激勵下的隨機運動。圖5(a)、(b)兩圖顯示在同一組激勵下，不同初值導致的運動不同，說明了有的運動能穿出安全域邊界，有的則不能，結合圖4(d)說明安全盆內部出現(xiàn)了分形特性。圖5(c)對應圖2(c)說明了即使系統(tǒng)在單純的隨機因素激勵下出現(xiàn)了振動的隨機特性，但是系統(tǒng)沒有發(fā)生混沌，則安全盆不會出現(xiàn)分形邊界。

4 結論

本文通過建立形狀記憶合金的連續(xù)光滑應力－應變模型后得到了簡支SMA梁的動力學模型，化簡后振動方程為一個具有負剛度的杜芬－范德坡模型，該模型受簡諧參激和白噪聲外激勵聯(lián)合作用。隨機Melnikov過程的計算給出了該系統(tǒng)發(fā)生混沌的必要條件判據(jù)。數(shù)值模擬了系統(tǒng)出現(xiàn)混沌時安全盆的邊界會出現(xiàn)分形特征。本文的工作意義主要體現(xiàn)在:

(1)通過計算系統(tǒng)發(fā)生混沌的激勵幅值條件為SMA梁的穩(wěn)定工作提供了理論參考。安全盆的邊界分形給判斷混沌提供了除Melnikov方法之外的依據(jù)。

(2)安全盆可以清晰的判斷初值對系統(tǒng)穩(wěn)定運行的意義，尤其在施加了噪聲干擾后，系統(tǒng)能夠安全工作的初值會減少，此研究意義在于:系統(tǒng)在較大激勵幅值下即使發(fā)生混沌，只要把初值取在安全盆內的安全區(qū)，系統(tǒng)的能量也不會超出許可限制。為系統(tǒng)的健康工作提供了參考依據(jù)。

[1]Tanaka K.A thermomechanical sketch of shape memory effect:one-dimensional tensile behavior [J]. Res Mechanics，1986，18:251 －263.

[2]Liang C，Rogers C A.A one-dimensional-thermo mechanical constitutive relation of shape memory materials[J].Journal of Intelligent Material System Structure，1990，1:207 －234.

[3]Boyd J G，Lagoudas D C.A thermodynamical constitutive model for shape memory materials[J].International Journal of P1asticity，1996，12:805 －873.

[4]Brinson L C.One-dimensional constitutive behavior of shape memory alloys:thermomechanical derivation with nonconstant material functions and redefined martensite internal variable[J].Journal of Intelligent Material Systems and Structures，1993，4:229 －242.

[5]Graesser E J，Cozzarelli F A.A proposed three-dimensional constitutive model for Shape memory alloys[J].Journal of Intelligent Material Systems and Structures，1994，14:78－89.

[6]Ivshin Y，Pence T J.Thermomechanical model for a one variant shape memory material[J].Journal of Intelligent Material Systems and Structures，1994，5:455 －473.

[7]Auricchio F，Lubliner J.Uniaxial model for shape-memory alloys[J].International Journal of Solids and Structures，1997，34:3601 －3618.

[8]Collet M，F(xiàn)oltete E，Iexcellent C.Analysis of the behavior of a shape memory alloy beam under dynamical loading[J].European Journal Mechanics，A-Solids，2001，20:615 － 630.

[9]Hashemi S M T，Khadem S E.Modeling and analysis of the vibration behavior of a shape memory alloy beam [J].International Journal of Mechanical Sciences，2006，48(1):44－52.

[10]Savi M A，Pacheeo P M，Braga M B.Chaos in shape memory two-bar truss[J].InternationalJournalofNon-Linear Mechanics，2002，37(1):1387 －1395.

[11]李映輝，張清泉.形狀記憶合金梁動力穩(wěn)定性[J].西南交通大學學報，2005，40(4):453 －456.

[12]張清泉，李映輝，姚 進.形狀記憶合金梁動力穩(wěn)定性及混沌運動[J].四川大學學報(工程科學版)，2004，36(5):30－36.

[13]Wu Z Q，Zhang Z H.Force displacement characteristics of simply supported beam laminated[J].Acta Mech.Sin，2011，27(6):1065－1070.

[14]葛 根，王洪禮，許 佳.形狀記憶合金梁的建模及混沌閾值計算[J].振動與沖擊，2012，31(12):103－107，119.

[15]Liu Z H，Zhu W Q.Homoclinic Bifurcation and Chaos in simple pendulum under bounded noise excitations[J].Chaos，Solitons and Fractals，2004，20:593 －607.

[16]Wiggins S.Global bifurcations and chaos:analytical methods[M].New York:Springer，1988.

[17]Lin H，Yim S C S.Analysis of a nonlinear system exhibiting chaotic，noisy chaotic，and Random behaviors[J].J.Appl Mech ASME，1996，63:509 －516.

[18]Gan C B.Noise induced chaos in a quadratically nonlinear oscillator[J].Chaos，Solitons ＆ Fractals，2006，30:920－929.