單向復合材料矩形截面非圓柱螺旋彈簧固有頻率的參數(shù)研究

郝 穎，虞愛民

(同濟大學 航空航天與力學學院，上海 200092)

非圓柱(錐形、桶形、雙曲形)螺旋彈簧的特性線具有很強的非線性，能夠適用于多種受限制的安裝空間，在工程實際中得到了大量的應用[1－3]。簧絲截面為非圓形的非圓柱螺旋彈簧，具有蓄存能量大、有效平緩應力分布、壓并高度低，壓縮量大等優(yōu)良性能[4]，被廣泛用于發(fā)動機閥門、離合器和自動變速等裝置上。

由于復合材料具有強度高、耐腐蝕、電絕緣性好、比重小、可設計性強等諸多優(yōu)點，在工程實際中逐漸開始使用復合材料來制備彈簧。但目前復合材料在彈簧制造領(lǐng)域的應用還非常有限，現(xiàn)有的嘗試多是用來加工板簧，對于應用范圍最廣的螺旋彈簧的研發(fā)很少[5]，而對于螺旋結(jié)構(gòu)更為復雜的非圓柱螺旋彈簧的研究則更為罕見。只有很少的文獻[6－8]涉及到此類問題，其中最重要的工作就是Yildirm[6]在文獻[9]的基礎上導出了各向異性材料空間曲桿的運動微分方程，然而她在方程中并沒有考慮桿件橫截面翹曲變形的影響。Yildirim[7－8]又利用傳遞矩陣法研究了單向復合材料非圓柱螺旋彈簧的自由振動，但研究中所考慮的簧絲截面均為圓形，因而無從考慮翹曲變形對自由振動特性的影響。文獻[10－11]已經(jīng)研究了各向同性材料非圓截面圓柱螺旋彈簧的自由振動問題，計算表明，即使對于此類彈簧，翹曲變形對固有頻率也有著較大的影響，在它們的振動分析中應該加以考慮。

鑒于目前對復合材料非圓截面非圓柱螺旋彈簧理論研究工作的缺乏和均未考慮翹曲變形的情況，本文首先把自然彎扭梁理論推廣到材料為各向異性的情況，導出了單向復合材料矩形截面非圓柱螺旋彈簧的運動微分方程，它們由14個變系數(shù)的一階偏微分方程組成。方程中不僅考慮了各種經(jīng)典效應的影響，而且首次考慮了簧絲截面翹曲變形的影響。此外，在文獻[12]的基礎上，可以導出單向復合材料矩形截面桿件的圣維南扭轉(zhuǎn)翹曲函數(shù)。在增加了廣義翹曲坐標和廣義翹曲力矩兩個自由度后，方程呈現(xiàn)出很強的剛性，本文采用改進的 Riccati傳遞矩陣法[13－14]對該彈簧的自由振動微分方程進行求解。

1 考慮翹曲效應的各向異性自然彎扭梁理論

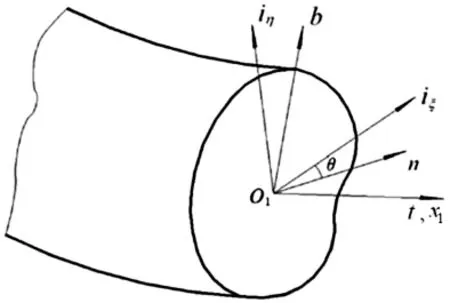
圖1 各向異性自然彎扭梁的幾何關(guān)系Fig.1 Geometry of naturally curved and twisted anisotropic beams

1.1 幾何關(guān)系和廣義虎克定律

設各向異性自然彎扭梁橫截面形心的軌跡是一根連續(xù)的空間曲線，曲線 l的切線，主法線和次法線單位矢量分別用t，n，b表示。為了考慮梁的初始扭曲，引入直角坐標系x1ξη，如圖1所示。x1軸與曲線的切線t重合，ξ軸與曲線主法線n之間的夾角記為θ，它通常是弧坐標s的函數(shù)。用iξ和iη表示O1ξ和O1η方向的單位矢量，則

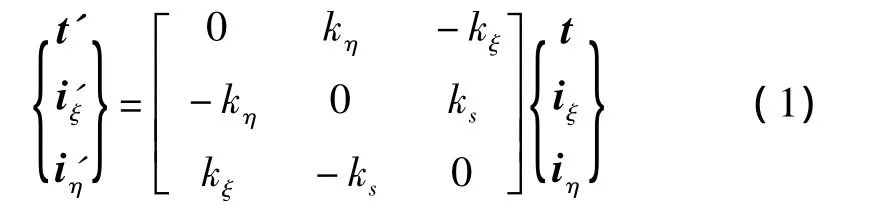
式中:上標撇號表示對弧坐標s的微分。kξ=k1sinθ，kη=k1cosθ，ks=k2+ θ'，k1，k2分別為曲線的曲率和扭率。

線彈性復合材料的廣義虎克定律定義如下[15]:

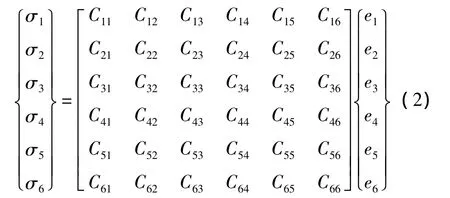
式中:

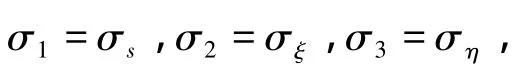
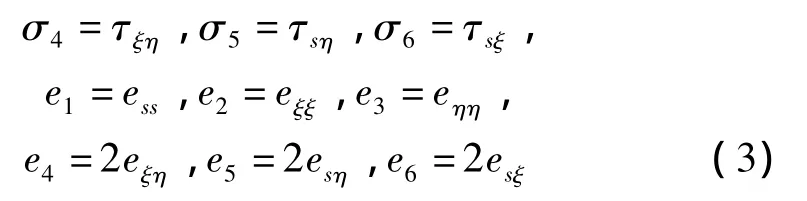
式中:σs，σξ，ση，τξη，τsη，τsξ分別為桿件內(nèi)任意一點的三個正應力和三個切應力，ess，eξξ和 eηη分別為相應方向的線應變，2eξη，2esη和 2esξ分別為該點在三個坐標平面內(nèi)的工程切應變。根據(jù)經(jīng)典層合板理論，應力與應變的關(guān)系可以簡寫為:

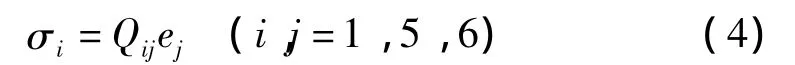
式中系數(shù)Qij的表達式參見文獻[6]。

1.2 本構(gòu)方程

對于單向復合材料，經(jīng)計算可得Q15=Q51=Q16=Q61=Q56=Q65=0。如果假設ξ，η軸為橫截面的形心主軸且不考慮桿件的初始扭曲，則有 I23=?Aξηdξdη=0，kξ=0，根據(jù)文獻[16]并利用式(4)，梁的內(nèi)力和內(nèi)力矩可以簡化為:

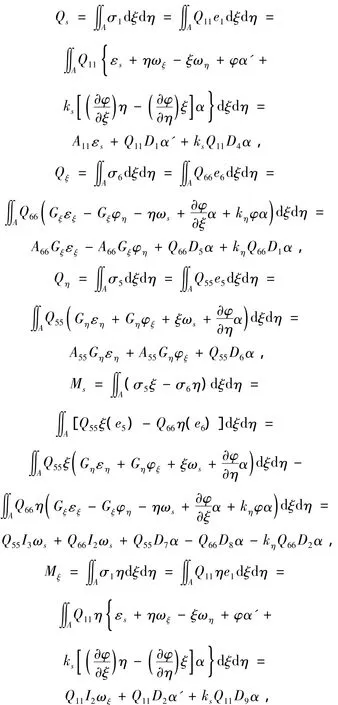
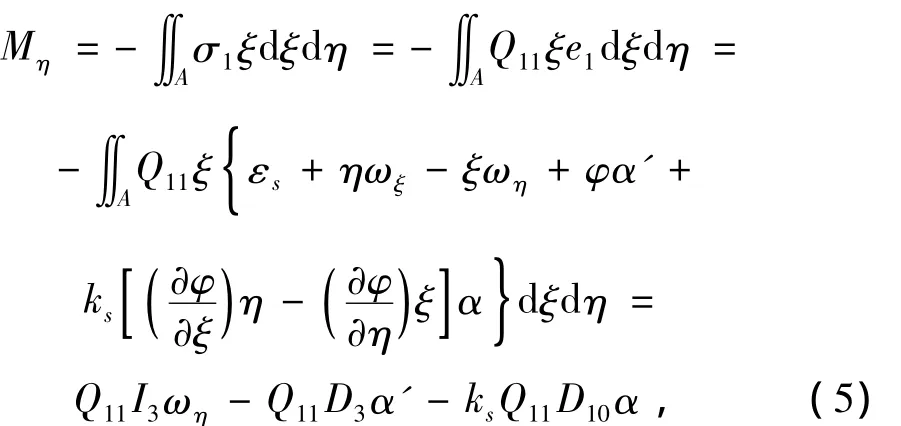
其中:

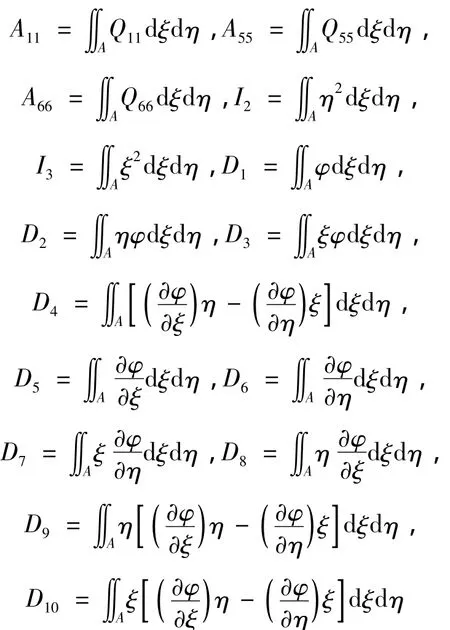
式中:εs，εξ和εη為桿軸上一點沿三個坐標方向的線應變，ωs，ωξ和ωη為桿軸單位長度的三個相對轉(zhuǎn)角。φ為圣維南扭轉(zhuǎn)翹曲函數(shù)，α是廣義翹曲坐標。引入廣義翹曲力矩的概念，其定義為:

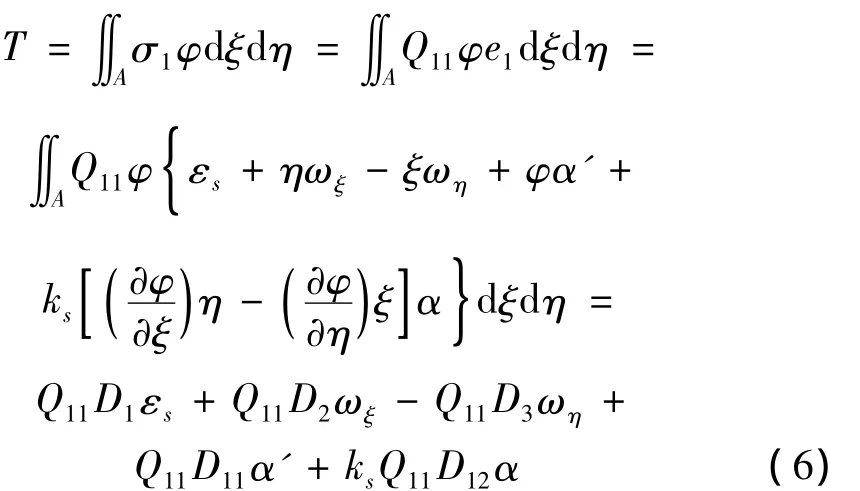
式中:

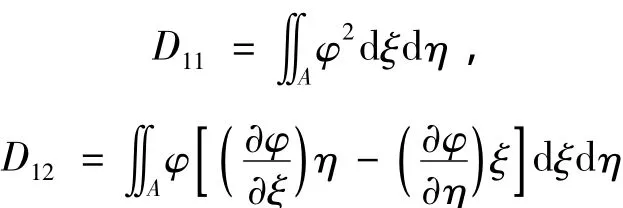
如果在方程組(5)和方程(6)中代入線應變和相對轉(zhuǎn)角的表達式[16]，則可以得到用六個位移函數(shù)us(s，t)，uξ(s，t)，uη(s，t)，φs(s，t)，φξ(s，t)，φη(s，t)和 α(s，t)表示的本構(gòu)方程。

1.3 運動微分方程

自然彎扭梁在考慮翹曲效應情況下的運動微分方程可以改寫為[16]:

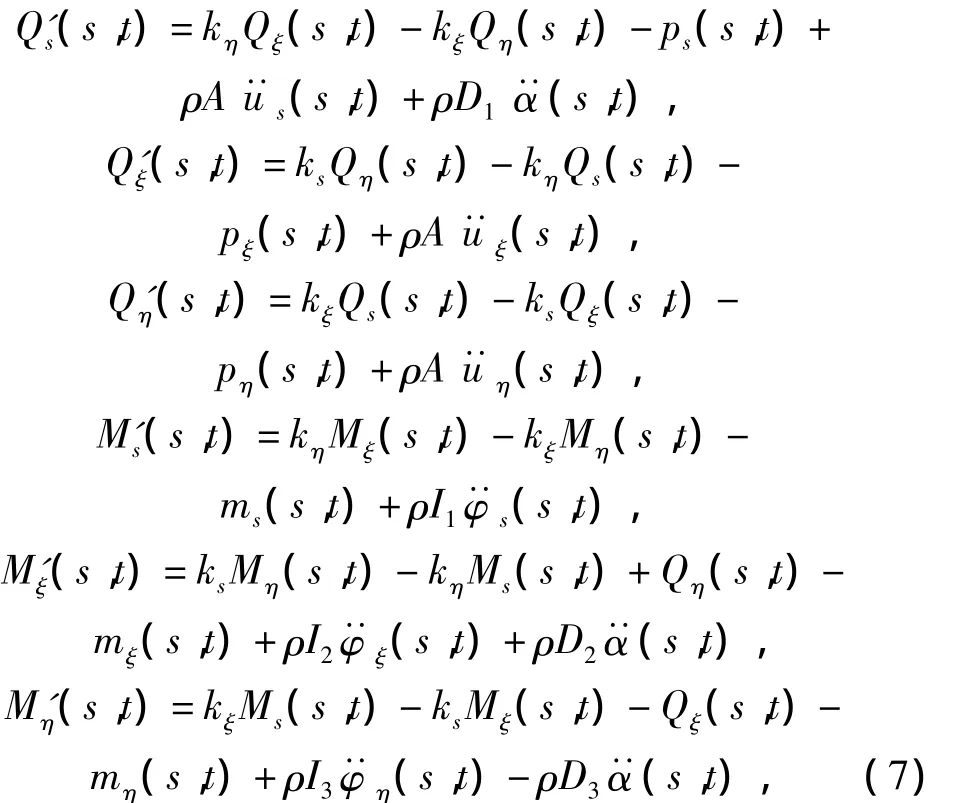
廣義翹曲力矩T(s，t)對弧坐標s的一階導數(shù)則為:

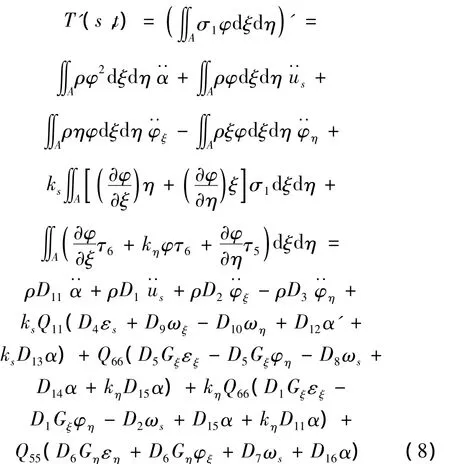
式中:

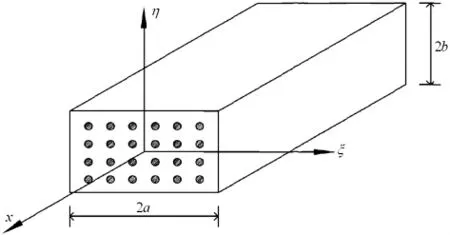
圖2 單向復合材料矩形截面桿件示意圖Fig.2 Schematic diagram of unidirectional composite bars with rectangular cross-section

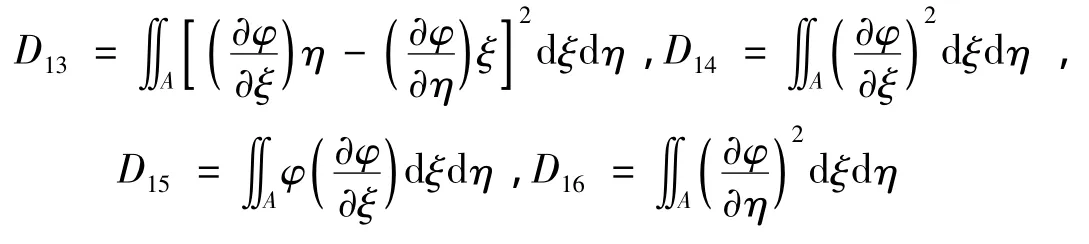
把方程組(5)、方程(6)和(8)中的線應變和相對轉(zhuǎn)角用六個位移函數(shù)代入，然后對方程組(5)和方程(6)進行聯(lián)立求解，可以得到各位移函數(shù)和廣義翹曲坐標關(guān)于弧坐標s一階導數(shù)的表達式，再利用這個結(jié)果來消去方程(8)中的這些導數(shù)，最后把所得方程和方程組(7)進行組合即可得到單向復合材料自然彎扭梁的運動微分方程，它們由14個變系數(shù)的一階(關(guān)于弧坐標s)偏微分方程組成。

1.4 單向復合材料矩形截面桿件的扭轉(zhuǎn)翹曲函數(shù)

設單向復合材料矩形截面桿件如圖2所示，記α2=Gxξ/Gxη，γn=nπ/2a，cn=16a2(－ 1)(n－1)/2/n2π2，n=1，3，5，…，在文獻[12]的基礎上可以導出單向復合材料矩形截面桿件的扭轉(zhuǎn)翹曲函數(shù)，即:

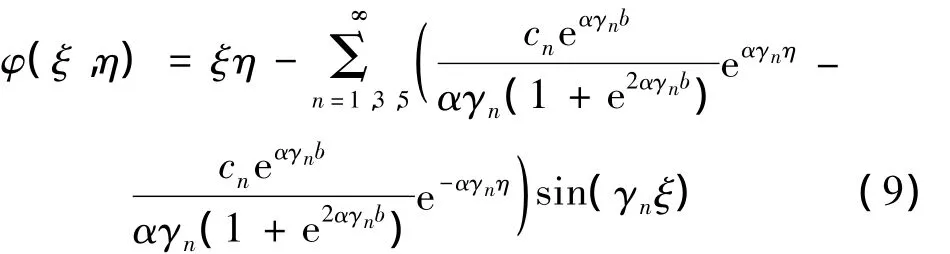
2 單向復合材料矩形截面非圓柱螺旋彈簧的運動微分方程

如圖3所示，非圓柱螺旋線是一條變曲率、變扭率的空間曲線，其幾何關(guān)系為:

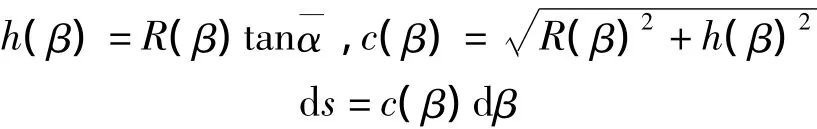
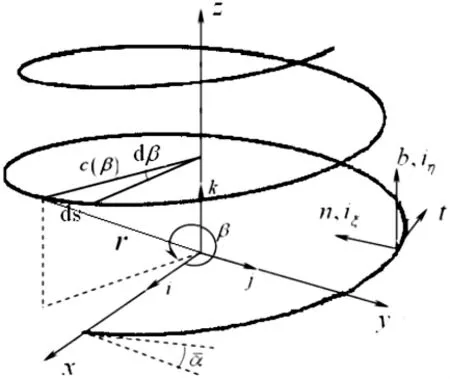
圖3 非圓柱螺旋線的幾何性質(zhì)Fig.3 Geometry of a typical non-cylindrical helix

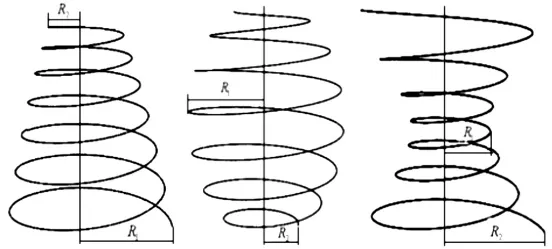
圖4 不同類型的非圓柱螺旋彈簧Fig.4 Different types of non-cylindrical helical springs

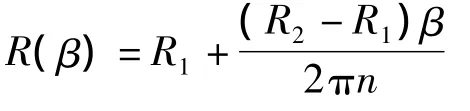
雙曲形和桶形彈簧螺旋線上任意點的半徑為:

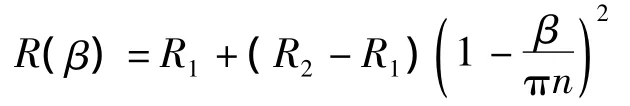
式中:R1和R2分別為螺旋線的最大和最小半徑(對錐形和桶形彈簧)或最小和最大半徑(對雙曲形彈簧)。如果令 ps=pξ=pη=ms=mξ=mη=0，同時假設單向復合材料矩形截面非圓柱螺旋彈簧作頻率為ω的簡諧運動[2]，利用 ds=c(β)dβ，并注意到與矩形截面翹曲函數(shù)φ(ξ，η)有關(guān)的積分 D1，D2，…，D16中有一些項等于零，則可以得到該彈簧的自由振動微分方程為:

在增加了廣義翹曲坐標和廣義翹曲力矩兩個自由度后，該方程呈現(xiàn)出很強的剛性，本文采用文獻[13－14]中改進的Riccati傳遞矩陣法對上述微分方程組進行求解，單元傳遞矩陣則采用Scaling-Squaring方法以及Pad'e逼近表達式進行計算。

3 數(shù)值算例

設兩端固支單向復合材料非圓柱螺旋彈簧的材料(T300/N5208)和幾何性質(zhì)分別為:E1=181 GPa，E2=E3=10.3 GPa，G12=G13=7.17 GPa，G23=3.433 GPa，μ12=0.28，ρ=1 600 kg/m3。矩形截面沿 ξ方向的邊長用2a表示，沿η方向的邊長用2b表示。螺旋線的最大、最小半徑R1，R2，彈簧的工作圈數(shù)n，螺旋角，剪切形狀因子 Gξ=Gη=0.842，扭轉(zhuǎn)翹曲函數(shù)如式(9)所示。

算例1

取R1=10 mm，R2=6 mm=5°，n=4，2a=1 mm，2b=0.4 mm。在對3種不同形狀的彈簧進行有限元分析時，均將其劃分成720個Solid46實體層合單元。為了與有限元結(jié)果進行比較，采用本文方法對彈簧的前5階固有頻率進行了計算。表1～3綜合了這3類彈簧在考慮與忽略翹曲影響得到的計算結(jié)果和有限元的結(jié)果。

算例2

取R1=10 mm，R2=6 mm=5°，n=4，表 4 綜合了不同寬高比對單向復合材料矩形截面錐形彈簧固有頻率的影響。

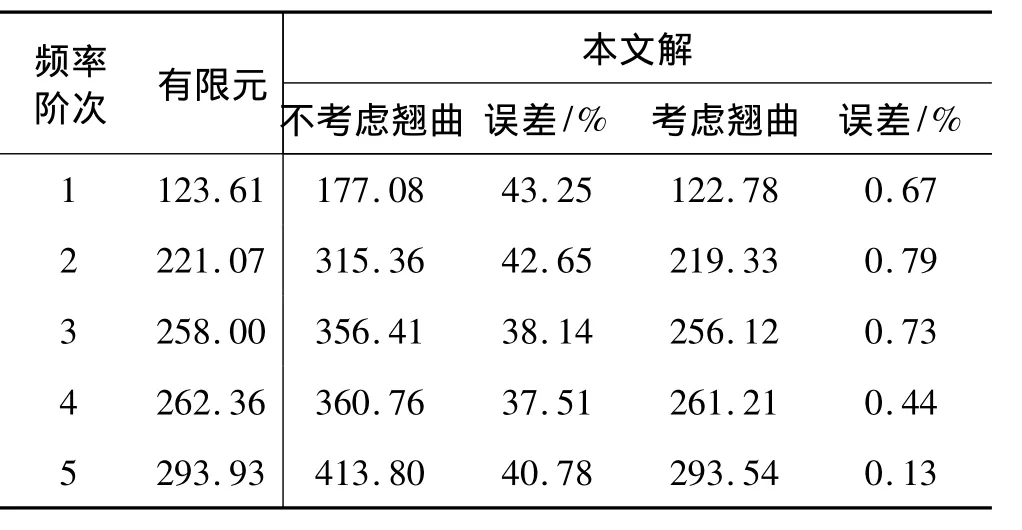
表3 單向復合材料矩形截面桶形彈簧的前五階頻率(R1=10 mm，R2=6 mm)Tab.3 The first five frequencies of unidirectional composite barrel springs with rectangular cross-section

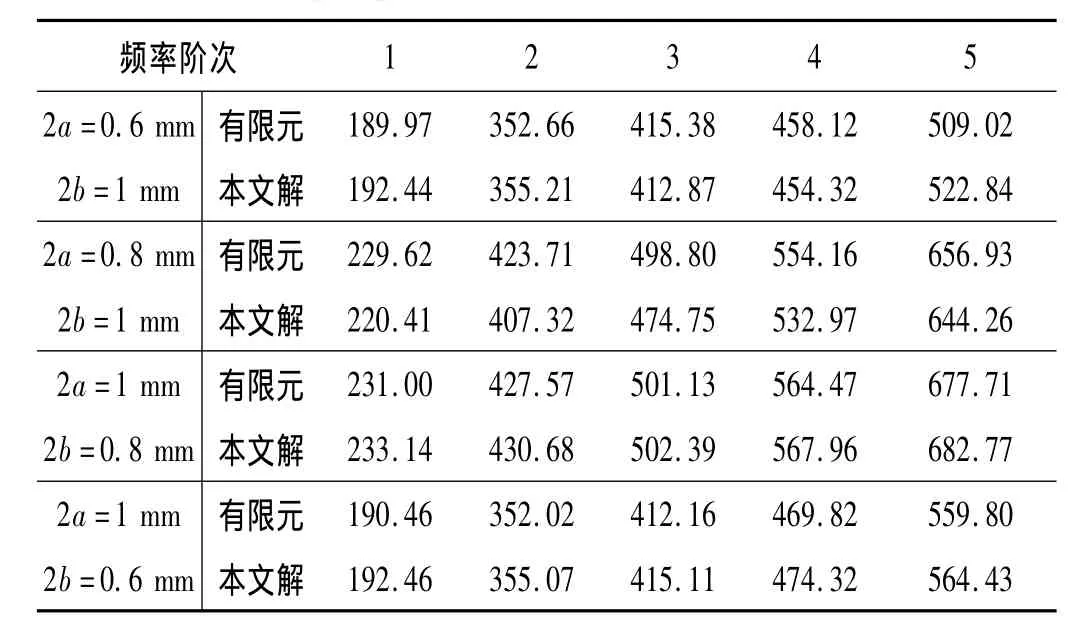
表4 寬高比a/b對矩形截面錐形彈簧頻率的影響Tab.4 The effect of the aspect ratio(a/b)on frequencies of conical-type spring with rectangular cross－section

算例3

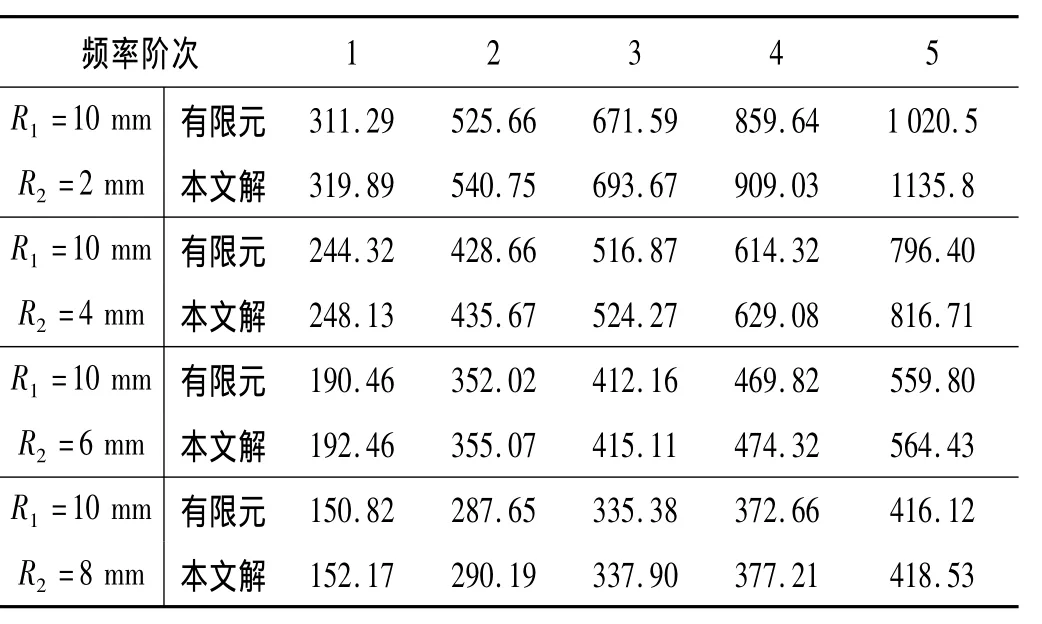
表5 R2/R1對矩形截面錐形彈簧頻率的影響Tab.5 The effect of(R2/R1)on frequencies of conical-type spring with rectangular cross-section

算例4

取 R1=10 mm，R2=6 mm，2a=1 mm，2b=0.6 mm，n=4，表6綜合了不同的螺旋角對單向復合材料矩形截面錐形彈簧固有頻率的影響。

表6 螺旋角對矩形截面錐形彈簧頻率的影響Tab.6 The effect of helix pitch angle)on frequencies of conical-type spring with rectangular cross-section

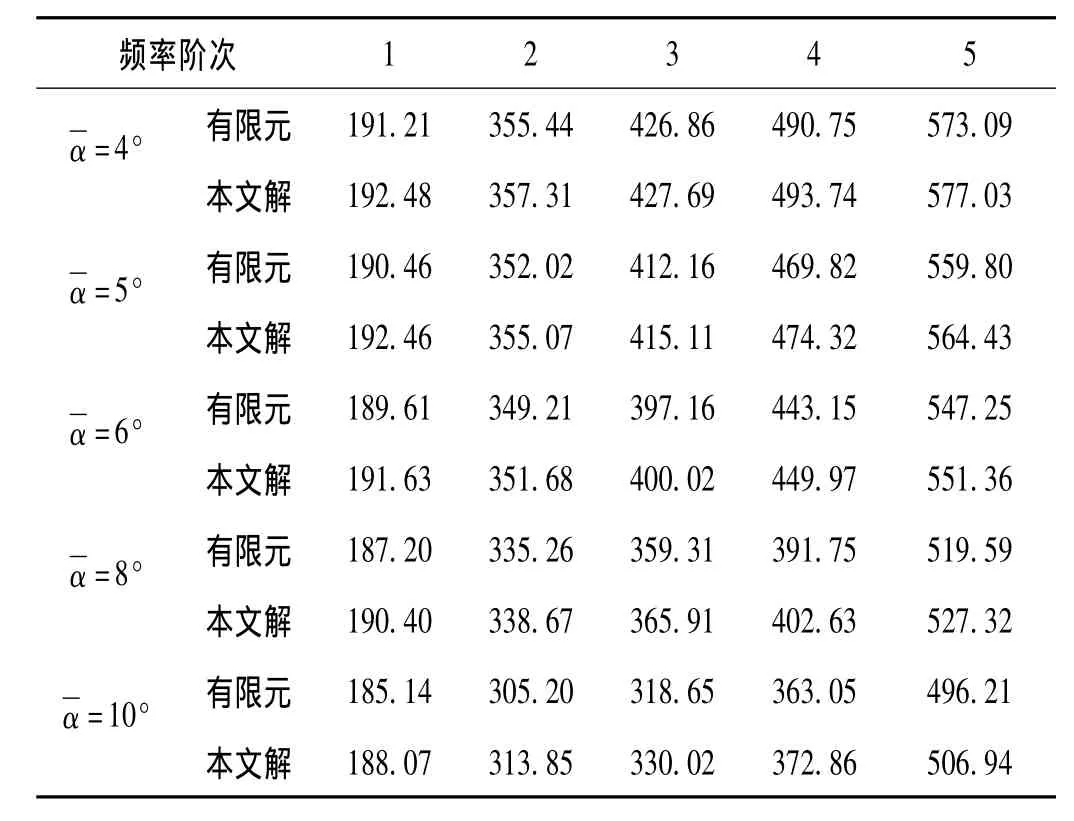
表6 螺旋角對矩形截面錐形彈簧頻率的影響Tab.6 The effect of helix pitch angle)on frequencies of conical-type spring with rectangular cross-section

頻率階次1 2 3 4 5 α =4° 有限元 191.21 355.44 426.86 490.75 573.09本文解 192.48 357.31 427.69 493.74 577.03 α =5° 有限元 190.46 352.02 412.16 469.82 559.80本文解 192.46 355.07 415.11 474.32 564.43 α =6° 有限元 189.61 349.21 397.16 443.15 547.25本文解 191.63 351.68 400.02 449.97 551.36 α =8° 有限元 187.20 335.26 359.31 391.75 519.59本文解 190.40 338.67 365.91 402.63 527.32 α =10° 有限元 185.14 305.20 318.65 363.05 496.21本文解 188.07 313.85 330.02 372.86 506.94

算例5

取 R1=10 mm，R2=6 mm，2a=1 mm，2b=0.6 mm=5°，表7綜合了不同的工作圈數(shù)對單向復合材料矩形截面錐形彈簧固有頻率的影響。

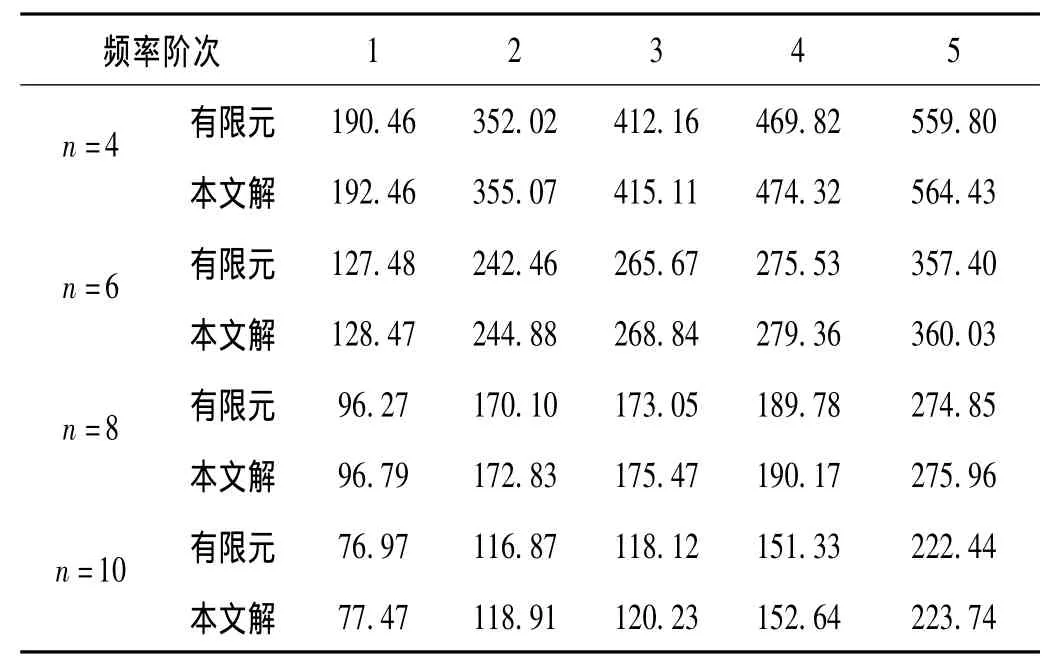
表7 工作圈數(shù)n對矩形截面錐形彈簧頻率的影響Tab.7 The effect of helix coil number(n)on frequencies of conical-type spring with rectangular cross-section

4 結(jié)論

本文采用改進的Riccati傳遞矩陣法研究了單向復合材料矩形截面非圓柱螺旋彈簧的自由振動特性，并首次在彈簧的控制方程中考慮了簧絲截面的翹曲變形對固有頻率的影響。同時，本文在較寬的范圍內(nèi)，給出了各種參數(shù)變化對矩形截面錐形彈簧固有頻率的影響:

(1)從表1～3可以看出，對于單向復合材料矩形截面的非圓柱螺旋彈簧，翹曲變形對其固有頻率具有重大的影響，是必須考慮的重要因素。不考慮翹曲變形時，計算所得前5階頻率的平均誤差為36.25% ～44.37%，而考慮翹曲變形后，計算所得平均誤差為0.65% ～1.24%。顯然，在考慮了翹曲變形后，用本文方法得到的解和有限元結(jié)果吻合得很好。

(2)當材料性質(zhì)和螺旋線的最大、最小半徑，螺旋角，工作圈數(shù)，以及截面面積都相同的情況下，雙曲形彈簧的剛度最大，其固有頻率最高，錐形彈簧次之，桶形彈簧的固有頻率最低。

(3)從表4可以看出，對于單向復合材料矩形截面錐形彈簧，固有頻率隨著矩形截面面積的增大而增大。

(4)從表5～7可以看出，隨著螺旋線的最小半徑、螺旋角和工作圈數(shù)的增大，彈簧的長度增加，而系統(tǒng)的剛度變小，則固有頻率也隨之減小。此外，隨著這些參數(shù)的增加，頻率開始變得相互接近。

[1]成 潔.車輛懸架系統(tǒng)的非線性振動特性研究[D].西安:西北工業(yè)大學，2006.

[2]凌愷夫.圓錐螺旋彈簧在機車車輛上應用的研究[J].株洲工學院學報，2001，15(3):48－51.LING Kai-fu.Application research of cone spiral spring on locomotive vehicle[J].Journal of Zhuzhou Institute of Technology，2001，15(3):48 －51.

[3]王紀瑞，左曙光，雷 鐳.基于MSC.Marc的中凸螺旋彈簧剛度特性研究[J].佳木斯大學學報(自然科學版)，2009，27(6):807－810.WANG Ji-rui，ZUO Shu-guang，LEI Lei.Simulation of static and dynamic stiffness characteristics of convex coil spring based on MSC.Marc[J].Journal of Jiamusi University(Natural Science Edition)，2009，27(6):807 －810.

[4]李 蕾.整枝機傳動機構(gòu)中矩形截面彈簧的研究[D].北京:北京林業(yè)大學，2008.

[5]隋 剛，范勇崢，仲偉虹，等.復合材料圓柱螺旋彈簧的制造與實驗研究[J].復合材料學報，2001，18(1):46－49.SUI Gang，F(xiàn)AN Yong-zheng，ZHONG Wei-hong，et al.Manufacture and experiment study of composite cylindroid spiral spring[J].Acta Materiae Composit AE Sinica，2001，18(1):46－49.

[6]Yildirm V.Governing equations of initially twisted elastic space rods made of laminated composite materials[J].International Journal of Engineering Sciences，1999，37(8):1007－1035.

[7]Yildirm V.Free vibration characteristics of composite barrel and hyperboloidalcoil springs[J].Mechanics of Composite Materials and Structures，2001，8(3):205 －217.

[8]Yildirm V.A parametric study on the natural frequencies of unidirectional composite conical springs[J].Communications in Numerical Methods in Engineering.2004，20:207－227.

[9]Kiral E，Ertepinar A.Studies on elastic rods subject to diverse external agencies-part III vibrational analysis of space rods[J].Journal of Pure and Applied Science，1974:55－69.

[10]Yu A M，Hao Y.Free vibration analysis of cylindrical helical springs with noncircular cross-sections[J].Journal of Sound and Vibration，2011，330(11):2628 －2639.

[11]郝 穎，虞愛民.考慮翹曲效應的圓柱螺旋彈簧的振動分析[J].力學學報，2011，43(3):561－569.HAO Ying，YU Ai-min.Vibration anslysis of cylindrical helical springs including wapring deformation effect[J].Chinese Journal of Theoretical and Applied Mechanics.2011，43(3):561－ 569.

[12]Xu R Q，He J S，Chen W Q.Saint-Venant torsion of orthotropic bars with inhomogeneous rectangular cross section[J].Computers＆ Structures，2010，92(6):1449－1457.

[13]劉保國.一維不定參數(shù)結(jié)構(gòu)系統(tǒng)的攝動Riccati傳遞矩陣方法及其應用[D].重慶:重慶大學，2002.

[14]王 正.Riccati傳遞矩陣法的奇點及其消除方法[J].振動與沖擊，1987，6(2):74－78.WANG Zhen，The singularity and its eliminating methods of Riccati transfer matrix method[J].Journal of Vibration and Shock，1987，6(2):74 －78.

[15]沈觀林，胡更開.復合材料力學[M].北京:清華大學出版社，2006.

[16]虞愛民，瞿志豪.自然彎曲與扭曲細長梁廣義變分原理的研究[J].上海冶金專科學校學報，1994，15(3):1－8.YU Ai-min，QU Zhi-hao.The study of variational principle in naturally curved and twisted slender beams[J].Journal of Technical College of Metallurgy.1994，15(3):1－8.