基于最小二乘法的曲線擬合研究

陳良波， 鄭亞青

（華僑大學(xué)機電學(xué)院，福建 廈門 361100）

基于最小二乘法的曲線擬合研究

陳良波， 鄭亞青

（華僑大學(xué)機電學(xué)院，福建 廈門 361100）

在工程應(yīng)用和科學(xué)實驗中，曲線擬合是對系統(tǒng)做出結(jié)論或預(yù)測的重要手段。因此擬合誤差變得非常重要，而最小二乘法作為曲線擬合最常用的方法，因其更為準(zhǔn)確、實用而被廣泛應(yīng)用。該文就最小二乘法對實驗所獲得的數(shù)據(jù)進(jìn)行曲線擬合，并對整個擬合過程進(jìn)行歸納和總結(jié)，其中一些主要步驟是在Matlab中實現(xiàn)的。

曲線擬合；最小二乘法；擬合誤差；Matlab

在許多實際工程應(yīng)用和科學(xué)實驗中，人們需要從一組測定的、有限個數(shù)據(jù)點中，設(shè)法找出一條連續(xù)光滑的曲線，以確定模擬函數(shù)的所有值，進(jìn)而得到所要的結(jié)論，或?qū)ο到y(tǒng)作出預(yù)測。目前，尋求模擬函數(shù)常用的方法主要有插值和擬合兩種。其中，插值法是通過已知點來確定模擬函數(shù)的方法，這要求模擬函數(shù)必須嚴(yán)格通過所有的已知點，因此其適用于數(shù)據(jù)準(zhǔn)確且數(shù)據(jù)量較小的情況，否則可能造成局部較大的誤差。由于在實際應(yīng)用或?qū)嶒炛校`差是不可避免的，所以為了不把原有誤差引入，人們經(jīng)常采用擬合來確定函數(shù)。擬合方法不要求模擬函數(shù)必須通過所有已知點，它追求的是所有點到模擬函數(shù)達(dá)到某種誤差指標(biāo)的最小化，因此其比較適合數(shù)據(jù)有誤差、數(shù)據(jù)量較大的情況。常用的誤差指標(biāo)有兩種：一是按照誤差向量的∞－范數(shù)定義稱為一致性數(shù)據(jù)擬合；另一種是按照誤差向量的2－范數(shù)定義，稱為最小二乘數(shù)據(jù)擬合［1］。本文是通過最小二乘數(shù)據(jù)擬合的方法來確定實驗數(shù)據(jù)的模擬函數(shù)。

1 最小二乘法曲線擬合原理

最小二乘法曲線擬合的基本思想是：使所有數(shù)據(jù)點與估計點（或稱擬合點）的誤差（如果是二維圖形誤差就是數(shù)據(jù)點與估計點的垂直距離）的平方和，如果所擬合的曲線能使該誤差平方和最小，這就得到最小二乘法擬合曲線［2］。其數(shù)學(xué)原理如下：

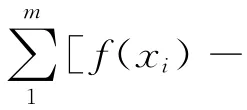
2 曲線擬合的主要步驟

2.1 確定擬合曲線的函數(shù)模型

在實際工程應(yīng)用和科學(xué)實驗中，有時很難確定參數(shù)之間存在著何種關(guān)系，是線性還是非線性，如果是非線性，那是多項式函數(shù)、冪函數(shù)、指數(shù)函數(shù)、對數(shù)函數(shù)等，甚至是它們的復(fù)合函數(shù)，有時還需要分段分析，因此在整個擬合過程中，擬合曲線函數(shù)模型的確定是最困難的。

對于擬合函數(shù)的模型確定，一般來說，主要有觀察法、近似法以及計算法［3］。目前用得較多的是觀察法。觀察法是利用數(shù)學(xué)專業(yè)知識對已知數(shù)據(jù)點的分布，初步確定其最可能的函數(shù)關(guān)系，該方法簡單、直觀。

2.2 確定法方程求解參數(shù)

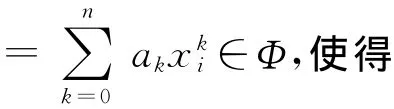
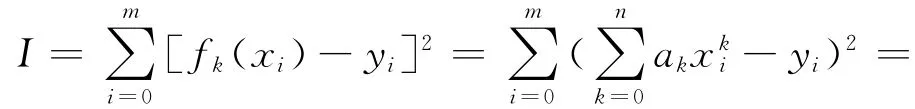
而公式（1）為多元函數(shù)，其最小值存在的必要條件是其對應(yīng)偏導(dǎo)等于零，由此可得，

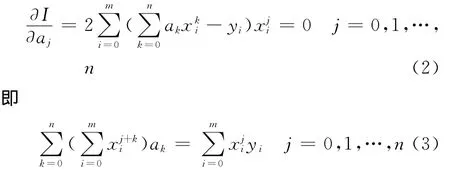
公式3稱為法方程，通過該方程可求出唯一解ak（k＝0，1，…，n），從而確定擬合函數(shù)。

此外，上述過程，也可以通過Matlab自帶的函數(shù)polyfit自動計算［4］。

2.3 曲線擬合性能檢驗

當(dāng)擬合曲線函數(shù)模型很難通過一般的方法確定時，往往需要通過分析若干可能的函數(shù)模型后，經(jīng)過實際計算才能選到較好的模型。一般來說最小誤差平方和越小說明曲線擬合越好，有些文獻(xiàn)也通過相關(guān)系數(shù)R的值來決斷擬合的優(yōu)劣［5］。

3 應(yīng)用舉例

在摩擦實驗中，當(dāng)量電壓為－285V時，伺服電機開啟后，時間與速度關(guān)系如表1所示，求速度與時間的擬合曲線及200ms時的加速度。

表1 10到500ms的轉(zhuǎn)速值Tab.1 From 10to 500ms speed value

（1）根據(jù)上述提供已知數(shù)據(jù)，以時間為橫坐標(biāo)，速度為縱坐標(biāo)，在Matlab畫出數(shù)據(jù)點示意圖，如圖1。Matlab代碼為

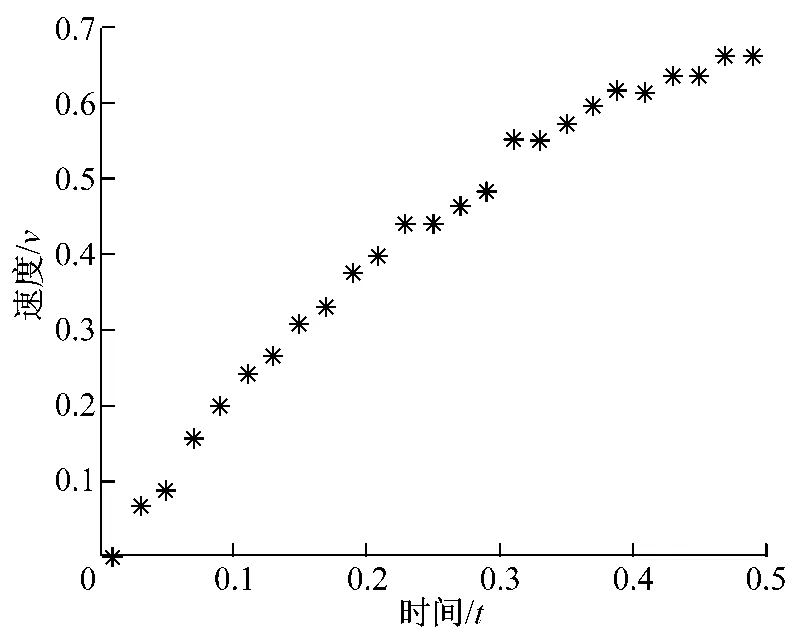
圖1 數(shù)據(jù)點示意圖Fig.1 Data point diagram

根據(jù)物理知識，當(dāng)加速度一定時，時間和速度是成一定比例，但本題不知道加速度如何變化，所以時間和速度可能不是線性關(guān)系，另外從數(shù)據(jù)點示圖1上看不出明顯的數(shù)學(xué)規(guī)律，所以對本題進(jìn)行了線性、多項式二次、三次、五次、冪函數(shù)、對數(shù)函數(shù)曲線擬合，從中得到最優(yōu)擬合。

（2）對各函數(shù)模型進(jìn)行曲線擬合

a）線性擬合：Matlab代碼如下：

得到線性擬合函數(shù)：y＝1.352 4x＋0.075 3

誤差平方和e＝0.039 3

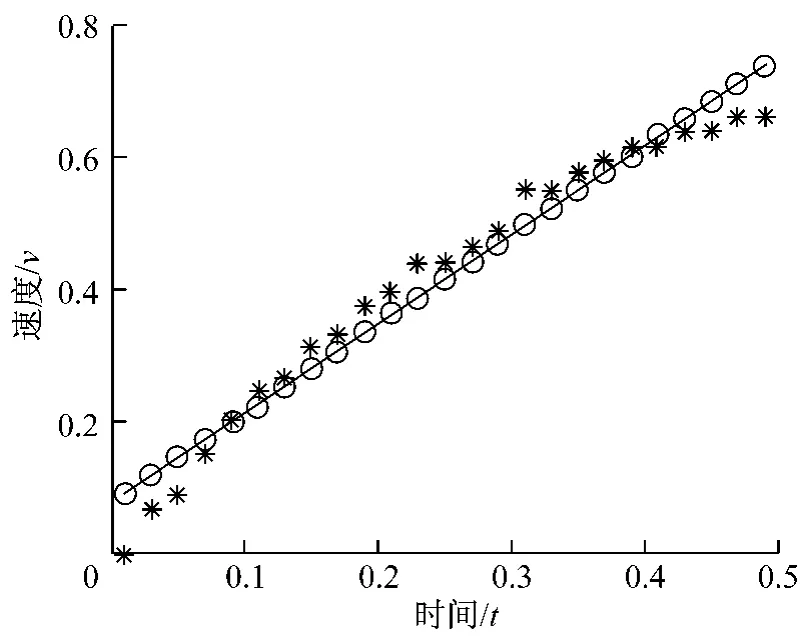
圖2 線性擬合Fig.2 Linear fitting

b）多項式二次擬合，得到擬合函數(shù)：y＝－2.052 4x2＋2.378 6x－0.010 3，誤差平方和e＝0.003 0，擬合圖形如圖3。

c）多項式三次擬合，得到擬合函數(shù)：y＝0.840 1 x3－2.682 5x2＋2.504 8x－0.015 5，誤差平方和e＝0.002 9，擬合圖形如圖4。

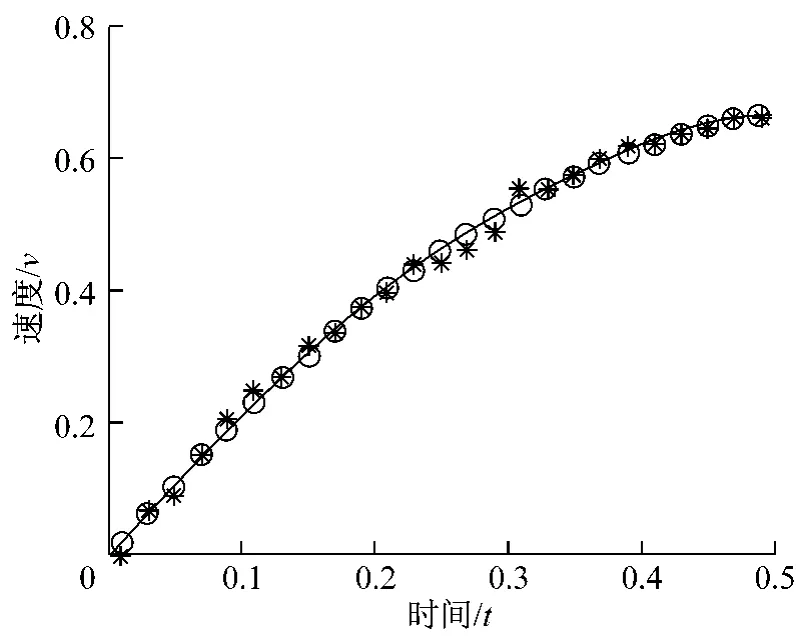
圖3 多項式2次擬合Fig.3 A2fitting polynomial

圖4 多項式3次擬合Fig.4 A3fitting polynomial

d）對數(shù)函數(shù)擬合，模型函數(shù)y＝a＋b＊log x，令t＝log x，因此對數(shù)模型函數(shù)就轉(zhuǎn)為線性函數(shù)的擬合y＝a＋b＊t，在Matlab實現(xiàn)，得到擬合函數(shù)y＝0.202 8＊log x＋0.753 9，誤差平方和e＝0.088 5，擬合圖形如圖5。

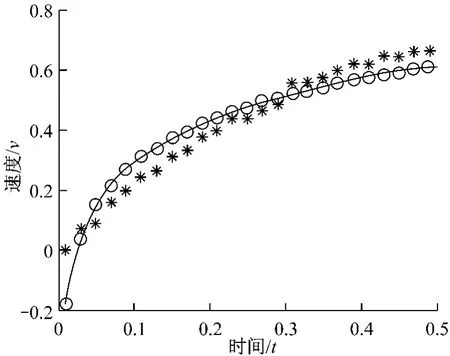
圖5 對數(shù)函數(shù)擬合Fig.5 Logarithmic function fitting

e）冪函數(shù)擬合，模型函數(shù)y＝axb，兩邊取對數(shù)得，log y＝log a＋b＊log x，令k＝log y，t＝log x，因此指數(shù)函數(shù)就轉(zhuǎn)為線性函數(shù)k＝log a＋b＊t的擬合，最后在Matlab實現(xiàn)，得到擬合函數(shù)y＝1.364 7x0.8339，誤差平方和e＝0.027 3，擬合圖形如圖6。

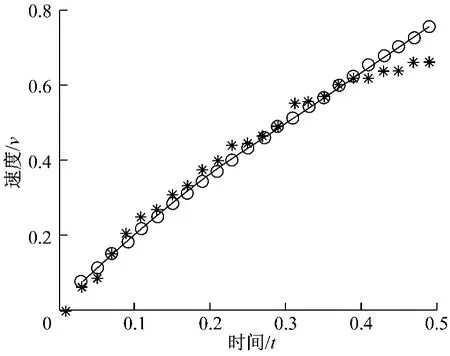
圖6 指數(shù)函數(shù)擬合Fig.6 Exponential function fitting

（3）各擬合函數(shù)評價

從下表2可以看出多項式二次、三次的擬合誤差平方和是最小，因此兩種曲線擬合是最優(yōu)的，不過由于多項式擬合次數(shù)越高，計算量就越大，若取過高，會將噪聲納入模型中，引起更大的誤差，結(jié)合本題實際及在誤差相差很小的情況下，比較傾向選擇多項式二次函數(shù)進(jìn)行擬合，因此對擬合函數(shù)求導(dǎo)得電機加速度方程y′＝－4.104 8x＋2.378 6，把200ms代入，可得到200ms處加速度為1.557 6 m／s2。

4 結(jié) 論

在工程應(yīng)用與科學(xué)實驗中有廣泛應(yīng)用的最小二乘法，能否準(zhǔn)確擬合出曲線是非常重要的。本文通過一個實例利用最小二乘法對已知數(shù)據(jù)進(jìn)行線性及非線性擬合，期間借助Matlab這個強大的計算機工具快捷實現(xiàn)目標(biāo)，整個過程詳細(xì)、準(zhǔn)確，為進(jìn)一步研究曲線擬合打下基礎(chǔ)。

表2 各擬合函數(shù)比較表Tab.2 The fitting function comparison table

［1］ 候媛彬.系統(tǒng)辨識及MATLAB仿真［M］.北京：科學(xué)出版社：2004.

［2］ 賈小勇，徐傳勝，白欣.最小二乘法的創(chuàng)立及其思想方法［J］.西北大學(xué)學(xué)報.2006，36（3）：507－511.

［3］ 王解先.最小二乘平差中的近似值問題［J］.工程勘探.2007（11）：48－49.

［4］ 郭利輝，朱勵洪，高巍.基于MATLAB的最小二乘法系統(tǒng)辨識與仿真［J］.許昌學(xué)院學(xué)報，2010，29（3）：24－27.

［5］ 周品，何正風(fēng).MATLAB數(shù)值分析［M］.北京：機械工業(yè)出版社，2009.

Study on Curve Fitting Based on Least Square Method

CHEN Liangbo， ZHENG Yaqing
（College of Mechanical Engineering and Automation，Huaqiao University，Xiamen 361100，China）

In engineering applications and scientific experiments，curving fitting is an important method to make a summary or prediction for a system.Therefore，the error of curving fitting becomes extremely important.The most popular method in curving fitting is least square method，which is widely used because it is more accurate and practical.The article curve－fits the data of experiment by way of least square method，and concludes and summarizes the whole process of curving fitting，in which some main procedures are processed in matlab.

Curving Fitting；Least Square Method；Error of Fitting；Matlab

O 241.5

A

1671－7880（2012）05－0052－04

2012－07－03

陳良波（1981— ），男，福建泉州人，工程碩士，主要從事摩擦模型與仿真研究。鄭亞青（1974— ），女，福建泉州人，副教授，博士，主要從事繩牽引機器人研究。