關聯白噪聲對細菌Logistic生長過程的影響

方次軍

（湖北工業大學理學院，湖北 武漢430068）

生物是一種復雜的非線性系統，具有潛在的隨機性.反應分子通過擴散匯聚在一起，且它們的運動被隨機碰撞所驅動，在生物系統中揭示非線性條件下噪聲產生的各種重要效應，研究這些效應的產生的條件及其應用，已成為生命科學發展中的一個重要前沿領域，其研究成果正在推動許多科學領域的發展和相互交叉.研究在一個培養皿里面生活著一種細菌，供給一定量的細菌生存所需的營養，設x為t時刻的細菌相對數目，根據Logistic生長方程，可給出細菌的生長方程［1］

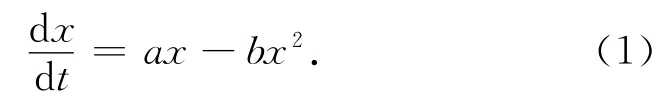
其中，a＞0，是細菌的固有生長率；b＞0，是限制細菌生長的抑制率.

方程（1）是一種理想的狀態，即細菌的生長不受外界的干擾.而實際情況是細菌的生長會不可避免地受到外界的環境的影響，比如溫度的變化，另外細菌本身的生長也會出現周期性漲落，這些干擾既會影響到a，也會影響到細菌數量的變化，從而導致噪聲.于是可用方程

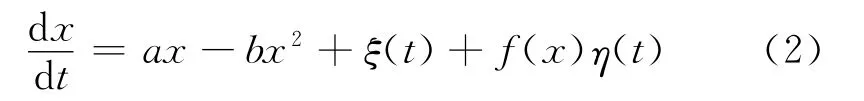
來描述細菌的實際生長過程.式中：ξ（t）是加性噪聲；η（t）是乘性噪聲.對于給定的隨機微分方程（2），關于變量x其勢函數為

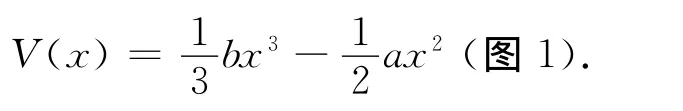
圖1 細菌Logistic生長過程（a＝1，b＝0.2）的勢函數圖

1 Fokker－Planck方程

對于給定的隨機微分方程

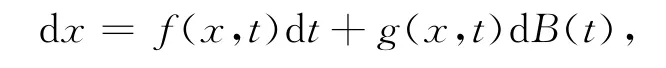
相應的Fokker－Planck（FPK）方程為［2］

其中

D為常數，它的值由

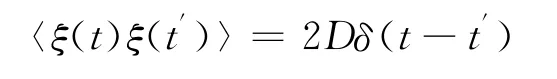
決定.FPK方程是一個拋物型線性變系數偏微分方程，它描述了擴散過程的轉移概率密度p（x，的進化和流動.當b（x，t）＝0時，方程（3）描述過程的確定性變化，a（x，t）＝0時，方程（3）描述純擴散運動.當FPK方程描述一個變量是局限于有限空間的“物理”隨機過程，那么，隨著時間t的增長，系統可能會趨于唯一的解，即穩態解.對于穩態解的研究具有重要的意義，其原因首先在于穩態解反映了系統的長時間行為，經過各種不同長短的瞬態過程后，系統就會被這種長時間行為所主導，所以在絕大多數時間內人們對系統進行測量得到的正是這類穩態解的性質.當系統演化經過很長時間后，認為它達到一個穩態，即.則p（x，t）與時間無關，記為p（x）.式（4）變為

兩邊對x積分得

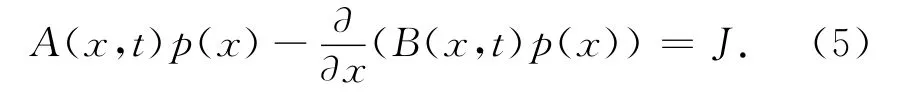
這里J為常數，代表穩態時概率流的強度.若認為系統是局限于隨機變量取有限值的的范圍，即概率分布滿足自然邊界條件［3］

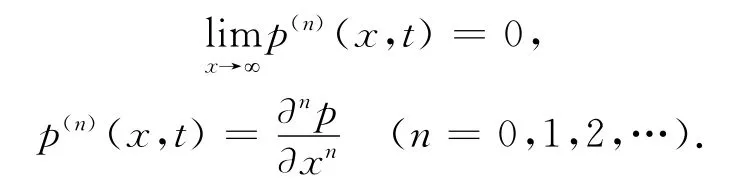
所以穩態概率流為0，即J＝0.代入式（5）解得

N為歸一化常數.

2 模型穩定性質的分析

首先給出方程（2）所滿足的統計性質：

其中，Q，M分別是乘性高斯白噪聲和加性高斯白噪聲的強度；0≤λ≤1是兩噪聲之間的關聯強度.由勢函數很容易得出其穩定解x＝0和x＝a／b，x＝0是平庸解，考慮最后的穩定解是x＝a／b，即環境所能供養細菌的最大相對數目.而對于考慮外界環境影響后，即方程（2）不容易直接從（1）來分析細菌的生長情況，但根據前面的（3）式筆者給出相對應的Fokker－Planck方程為［4］

這里p（x，t）是細菌在t時刻相對數目為x的概率密度.設

這里

故

從而

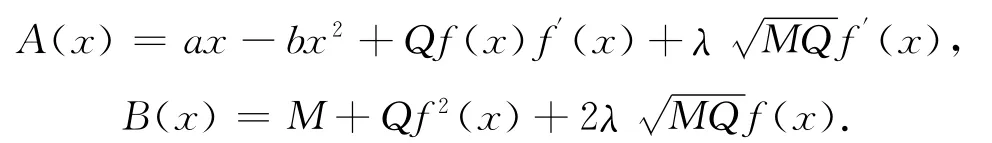
當系統隨著時間的演化，由方程（5）可得到穩態概率密度分布

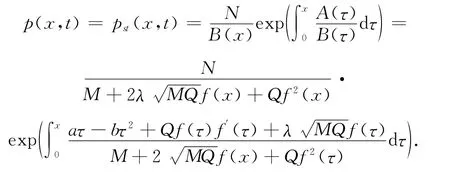
3 計算和分析

對于式（2），由式（6）可得到p（x，t）的極值所滿足的條件為可以得到A（x）＝B′（x）.從而得到式（2）應滿足

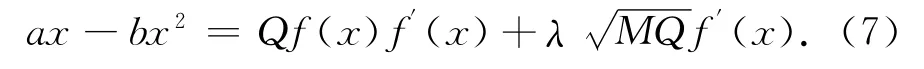
不妨取f（x）＝x進行研究，由式（7）得

當λ＝0時，即噪聲ξ（t）與η（t）沒有關聯，解得可見，乘性噪聲對p（x，t）的極值的位置有影響，加性噪聲對其沒有影響.

圖2是穩態概率分布和噪聲關聯強度之間的關系.λ＝0（兩噪聲沒有關聯時），穩態的概率分布一個峰值，位置大約在x＝5附近，當λ逐漸增大時，峰值逐漸下降，而在x＝0處的分布逐漸上升.圖2中的參數為a＝1，b＝0.2，Q＝0.1，M＝2［5，6］.

圖2 穩態概率分布和噪聲關聯強度之間的關系

從圖3中可以看出，隨著加性噪聲的增強，峰值的高度逐漸下降，但是兩邊的取值上升，但峰值的位置依然位于x＝4.8左右.可見加性噪聲使概率密度更加均勻，但它也會導致系統固有生長規律的破壞.從這種意義上看，加性噪聲對概率密度具有擴散作用［7］.圖3中的參數為a＝1，b＝0.2，Q＝0.1，λ＝0.

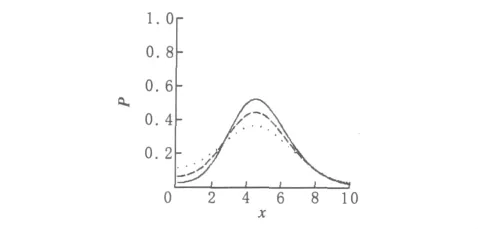
圖3 概率密度分布和加性噪聲強度之間的關系

圖4 表明概率密度分布和乘性噪聲強度之間的關系.當Q＝0.5時，峰值在x＝2.5附近，隨著乘性噪聲的減弱，峰值向右進行移動.從而可發現，乘性噪聲會抑制細菌的生長，干擾了細菌的固有生長規律.從這種意義上看，乘性噪聲對概率密度分布呈現漂移作用.圖4中的參數為a＝1，b＝0.2，M＝0.1，λ＝0.

圖4 概率密度分布和乘性噪聲強度之間的關系

4 結論

在細菌的Logistic生長過程中，筆者考慮了兩種噪聲的干擾作用，通過用Fokker－Planck方程，分別討論了加性噪聲以及乘性噪聲對細菌生長的影響.結果表明噪聲的關聯程度越高，越不利于細菌的生長；另一方面，加性噪聲改變了峰值，對概率密度分布具有擴散作用；乘性噪聲導致峰值的左右移動，對概率密度分布呈現出漂移作用.

［1］徐克學，生物數學［M］.北京：科學出版社，2005.

［2］LIN Y K，Cai G Q.Probabilistic structural dynamics［M］.Berlin：Heidelberg，1995.

［3］胡 崗.隨機力與非線性系統［M］.上海：科技教育出版社，1994.

［4］Bao－Quan Ai，Xian jun Wang，Guo－tao Liu，et al.Correlated noise in a logistic growth model［J］.Phys Rev E，2003，67（2）：90－93.

［5］楊琪瑜.單種群生長的廣義Logistic模型中參數的一種估值方法［J］.生物數學學報 ，1997（4）：316－320.

［6］桂占吉.生物動力學模型與計算機仿真［M］.北京：科學出版社，2005.

［7］艾保全.生物系統中的噪聲效用的研究［D］.廣州：中山大學圖書館，2004.