基于容差模型的發動機懸置系統穩健優化設計
王歆侃
(1.合肥工業大學 噪聲振動工程研究所,合肥 230009;2.安徽省汽車NVH與可靠性重點實驗室,合肥 230009)
人們對汽車乘坐的舒適度要求越來越高,發動機是汽車主要的振源,其振動經懸置系統傳遞給車架或車身,因而發動機懸置系統的參數設計對汽車整車減振來說非常重要。對于發動機懸置系統的優化設計,可以從不同角度提出目標函數和約束條件,并建立不同的數學模型。常見的目標函數主要有:發動機懸置系統六自由度完全解耦或是部分解耦,移頻使系統固有頻率處在合理的區間,系統的支反力(矩)最小或是傳遞率最小。考慮到研究的車型上的懸置位置和安裝角度已經確定,因而以懸置的剛度為設計變量,主要從移頻且使懸置系統部分解耦來進行多目標參數優化設計。懸置廠商提供的懸置墊,懸置剛度參數一般都有很大的可變性,主要來源于懸置材料的變化和懸置幾何形狀的變化。另外在懸置與支架等的裝配過程中,往往會產生預應力以及懸置形狀的扭曲,也將造成懸置剛度值的變化[1]。傳統的確定性解耦優化方法往往忽略了懸置剛度值的可變性,忽略了剛度偏差對懸置系統解耦的影響,使實際的工況下解耦效果很不理想。基于對懸置參數不確定因素影響的考慮,應該選擇一種方法一方面尋求目標函數的最優值,另一方面應該考慮設計變量的誤差等不確定因素,這就需要我們在優化設計中結合穩健設計的思想,即穩健優化設計。本文將穩健優化設計應用于發動機懸置系統的解耦優化中,充分考慮了各種干擾和設計變量的變差情況,不僅保證設計結果的合理性,同時也保證設計結果對懸置參數的不敏感性。同時利用Monte Carlo方法對結果進行分析驗證,對懸置剛度對系統性能的影響程度進行研究。
1 穩健優化設計模型
傳統確定性優化模型為:
式中:x,xL,xu分別為設計變量及其上下界; f (x)為目標函數;gi(x)(j=1,2,L,m)為 m 個約束函數。
穩健優化設計中,不僅考慮目標函數均值μf變化,而且要考慮目標函數的標準差σf的變化。均值μf和標準差σf的計算,可以通過泰勒級數展開來近似。考慮變量相互獨立,則目標函數的均值和標準差分別為:
對于約束函數,由于變量變化因而引起約束的變化,于是原問題的約束變為:
同時為了表示設計變量偏離的可行性,相應的設計變量的邊界變為:
(2)、(3)式中 n 為任意常數,當 n=3,x隨機變差時,其設計的可行率可達到,能滿足實際要求。
綜上,穩健優化模型為[3]:
2 發動機懸置系統優化模型
2.1 懸置系統理論模型
發動機懸置系統可簡化模型為:通過三個或四個三維的粘—彈性元件懸置支承在車架上,具有六個自由度。圖1為四點懸置布置模型。發動機總成的坐標系原點選在總成質心處,平行于曲軸中心線為X軸,指向發動機前端,Z軸平行于氣缸中心線,指向發動機缸蓋,Y軸按正交坐標系的右手定則確定。θx、θy、θz分別為繞 X 軸、Y 軸和 Z 軸的轉角。
利用拉格朗日方程可推導出系統振動微分方程為:
式中:[M ] 為系統的質量矩陣, [K ]為系統的剛度矩陣,[C ]為系統的阻尼矩陣,{q }=[x,y,z,θx,θy,θz]T為六個廣義坐標列向量, {F(t) }= [ fx,fy,fz,fθx,fθy,fθz]T為系統所受激勵向量。
對系統進行固有頻率和固有振型的計算,只需考慮無阻尼自由振動情況,系統微分方程為[M ][K ]{q}={0 }, 可計算得到懸置系統的六階固有頻率 ωj(j=1,2,L,6)和固有振型[φ ]。
2.2 能量法解耦
發動機懸置系統六自由度振動耦合往往導致發動機振幅加大,振動頻帶過寬。由此需要對其進行解耦設計。從能量的角度去評價懸置系統的耦合程度[4,5],由振動微分方程得到的系統的固有頻率和固有振型。當系統以第j階模態振動時,定義能量分布矩陣為:
式中:φ(k,j),φ(l,j)分別為第 j階振型的第 k 個和第l個元素;M(k,l)為系統質量矩陣的第k行、第l列元素;ωj是第j階固有頻率。
當系統以第j階模態振動時,第k個廣義坐標分配的能量占系統總能量的百分比:
當其值為100%,則系統作第j階模態振動時能量全部集中在k個廣義坐標上,此時,該階模態振動完全解耦。
2.3 懸置系統穩健優化模型
設計變量:發動機懸置系統特性與發動機及其變速箱等的質量,轉動慣量,懸置的安裝位置、安裝角度及其懸置主剛度值等因素有關。但是考慮到發動機和變速箱的本身的特性不能改變,同時懸置的安裝位置和角度已經確定,故而以懸置的主剛度值K1、K2、L、Ks(i=1,2,L,s)為設計變量,其中 s 為懸置主剛度個數。
優化目標:
式中:Eθx、Ez分別為側傾自由度上能量百分比和垂向自由度上能量百分比;w1、w2分別為側傾自由度上能量百分比和垂向自由度上能量百分比的加權因子。
約束條件:(1)懸置位移不能過大,過大的位移既容易使懸置剪切破壞,又使使用壽命降低,因而懸置主剛度不能過小,即(i=1,2,L,s);(2)懸置系統的最大固有頻率必須小于發動機自身激勵頻率1/的,才能起到隔振效果 。最小激勵頻率為怠速下的著火脈沖f=N·n/30C(N為汽缸數,n為曲柄轉速(r/min),C為沖程數),使有更好的隔振效果,則取懸置系統最大固有頻率為fmax≤N·n/30C。另外還需要避開車身的扭轉振動頻率、車身垂直跳動頻率、路面激勵頻率等,綜上取懸置系統固有頻率范圍為5≤f≤N·n/30。即:
綜上,由式(2)~(5)將以上模型轉化為穩健優化模型:
式中:n取為3。
2.4 最優化方法
考慮到該優化模型為兩目標優化問題,需要使用多目標優化算法。同時該模型設計變量多,優化目標與設計變量之間的函數關系復雜,存在許多局部最優解,需要選用合適的最優化算法。遺傳算法隱含著并行性,能夠同時搜索到多個局部最優解,利于找到全局最優解。而如果將多目標問題通過加權組合法等轉化為單目標問題,則無法發揮遺傳算法的優勢。將Pareto最優解方法和遺傳算法結合構成多目標優化設計的Pareto遺傳算法[6],能計算得到多目標優化問題的Pareto最優解集。此時從得到的最優解集中,根據具體的設計要求,選出最符合要求的解作為最終的設計結果。因而選擇Pareto遺傳算法來進行發動機懸置系統穩健設計。
3 優化實例
對于某具體的車型,該發動機為六缸四沖程的發動機,懸置系統為四點平置,左右對稱布置。其怠速為n=800 r/min,則其點火脈沖頻率為f=N·n/30C=40 Hz,則該懸置系統的固有頻率要滿足fmax≤N·n/3=28.3 Hz。懸置系統的質量參數、定位參數及其剛度參數分別如表1~3所示,優化前系統的固有頻率及能量分布如表4所示。

表1 懸置系統質量參數 kg·m2

表2 懸置定位參數 mm
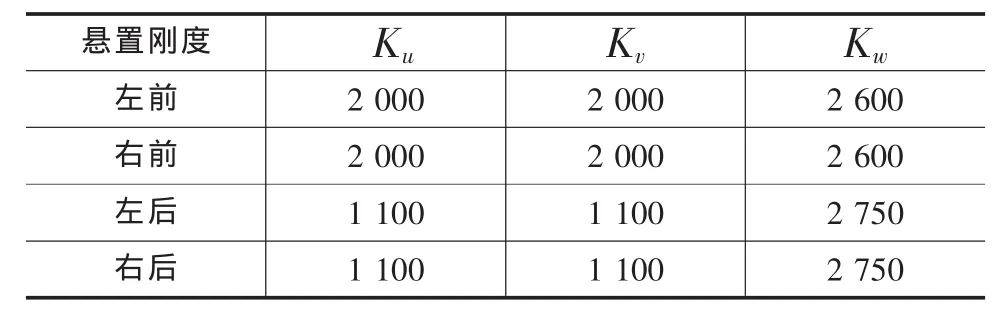
表3 優化前各懸置剛度值 N/mm
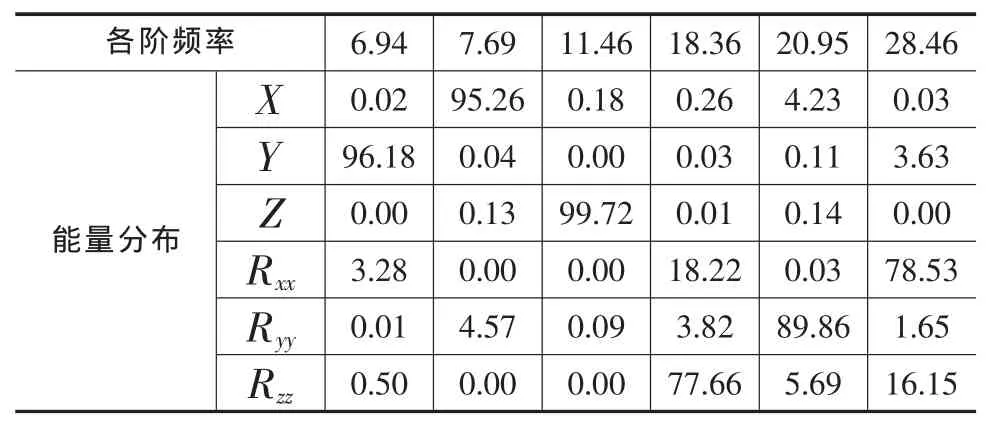
表4 優化前系統固有頻率與能量分布 Hz
由表4可以看出,部分頻率分布間隔過小,最高固有頻率過大,且各轉動軸方向的解耦度較低,其中側傾方向的解耦度只有78.53%,耦合較嚴重,需要改進。
采用Monte Carlo法分析懸置剛度對振動耦合能量分布的影響。假定剛度值按正態分布,變化范圍±10%,以4個懸置的剛度作為自變量對原系統進行魯棒性分析,經過1 000次隨機試驗分析,得到垂直和側傾方向解耦度的Monte Carlo圖,如圖2和圖3所示。
可以看出,垂直方向的解耦度分布較合理,最低與最高解耦度差值為 4.19%,標準差為0.6%,而側傾方向的解耦度分布不甚合理,最低與最高解耦度差值為 15.25%,標準差為 2.39%,穩健性較差。
利用穩健優化設計模型,采用Pareto遺傳算法,對動力總成懸置系統的剛度參數進行優化,優化后各懸置剛度值如表5所示,系統各階固有頻率與能量分布如表6所示。
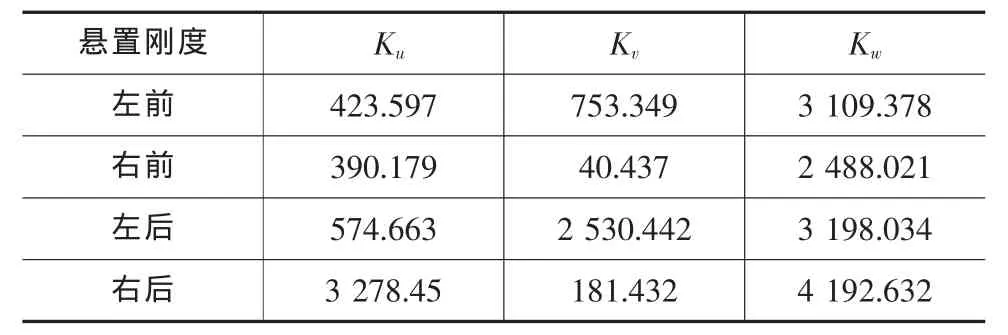
表5 優化后各懸置剛度值 N/mm
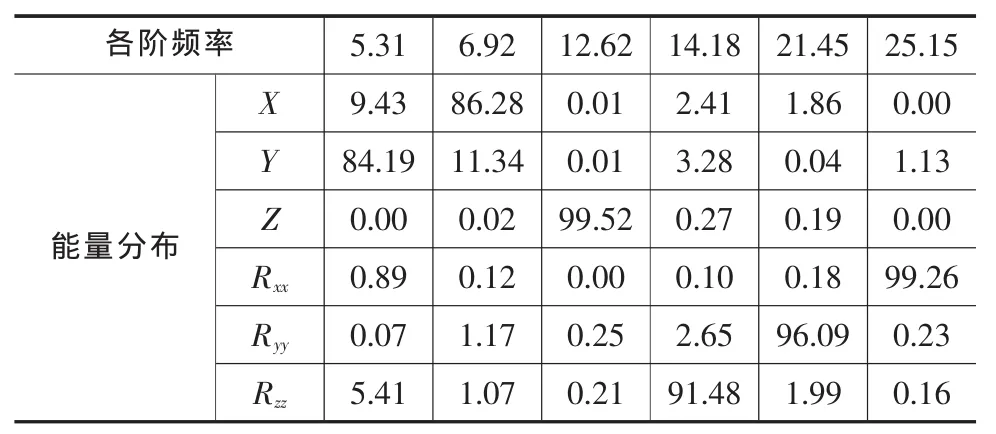
表6 優化后系統固有頻率與能量分布 Hz
可以看出,與優化前相比,系統的各階固有頻率分布更加合理,最高頻率有了較大的降低,各平動方向的解耦度有所降低,但各轉動方向解耦度有了較大的提高,其中主要的側傾方向由原來的78.53%提高到99.26%,系統的振動解耦有了較大的改善。
用同樣的參數和方法對優化后的結果進行Monte Carlo分析,結果如圖4和圖5所示。
可以看出,優化后的垂向解耦度分布仍較合理,而側傾方向的解耦度分布,最低與最高差值只有5.65%,標準差為0.6%,穩健性有了較大的提升。
4 總結
懸置剛度值的變差在實際中不可避免,懸置剛度值容差的減小意味著制造成本的提高。在不增加成本的前提下,需要有更好的方法對發動機懸置系統進行優化設計。本文在考慮懸置剛度變差的情況下,從解耦的角度,進行發動機懸置系統穩健優化設計。并且對結果進行Monte Carlo法分析,來決定優化結果在實際中的可行性。由文中的實例分析可得,穩健優化設計的結果比較滿意。
[1] M Qatu,M Siraft and F Johns.Rostness of powertrain mount system for noise,vibration and harshness idle[J].Automobile Engineering,2002.
[2] 陳立周.穩健設計[M] .北京:機械工業出版社,2000.
[3]徐石安.汽車發動機彈性支承隔振的解耦方法[J].汽車工程,1995,17 (4):198-204.
[4]王景蓉,陳無畏.轎車動力總成NVH性能分析及懸置優化[J].汽車科技,2008,4:26-30.
[5]夏露,高正紅,蘇偉.Pareto遺傳算法在氣動外形優化中的應用[J].空氣動力學學報,2007,25(2):194-198.

