客車車架有限元分析及尺寸優化

王 松 ，嚴運兵 ，張勝蘭

（1.武漢科技大學 汽車與交通工程學院，武漢 430081；2.湖北汽車工業學院 汽車工程系，十堰442002）

車架的剛度和模態是評價車架性能的兩個重要指標，車架必須有足夠的靜剛度以保證其裝配和使用要求，同時必須有合理的動態特性以控制振動和噪聲，另外，車架還要盡可能輕以降低成本、提高燃油經濟性和動力性［1］。如何在保證剛度和模態性能的前提下使車架的質量盡可能低是車架設計的一個重要環節。通過有限元方法可以分析計算出車架的彎曲、扭轉剛度和模態振型，并可以此為基礎對車架進行結構優化。

1 基于HyperWorks的有限元建模

本文研究的車架長約7.65 m，寬約0.85 m，高約0.85 m，由下面兩根主縱梁、上面兩根副縱梁、尾部兩根行李托架和上下1根橫梁組成，結構如圖1所示。

1.1 網格劃分

使用優秀的前處理工具HyperMesh進行網格劃分，車架的大部分都是薄壁件，于是采用殼單元進行建模，以四邊形為主，三角形為輔。劃分網格前先抽取薄壁零件的中面，再在中面上劃分網格。考慮到車架的實際尺寸，有限元模型的精確度，單元尺寸取10 mm。車架的結構比較復雜，零件間的連接方式是焊接、鉚接和螺栓連接。為了簡化模型而又不失真實性，選用1D的RIGID剛性單元（RBE2）模擬各種連接。最后，整個車架被劃分為138 167個殼單元，2 577個RIGID單元，網格模型如圖2所示。

1.2 材料與屬性

對于殼單元建模而言，網格劃分完畢后，需要賦予材料參數和厚度參數，才算建立起有限元力學模型。本車架鋼材號為DL510，有限元計算時的材料參數：彈性模量E=2.1×105MPa；泊松比μ=0.3；密度 ρ=7.8×109ton/mm3；板件厚度為 1.5 ～8.0 mm不等。

2 剛度分析

2.1 彎曲剛度分析

參照車架剛度試驗方法來模擬彎曲剛度與扭轉剛度的邊界條件［2］。

計算彎曲剛度時，約束前后橋在車架縱梁上的豎直投影點的垂直位移，在前后約束中點處施加一垂直向下的集中力F，讓車架模擬簡支梁的結構產生純彎曲變形，車架彎曲剛度的邊界條件如圖3所示。

車架的彎曲剛度計算公式如下：

式中：CB為彎曲剛度（Nm2）；F 為集中載荷（N）；f為載荷作用處的撓度（m）；a為軸距（m）。

當F=1 000時，車架的變形結果如圖4所示。車架載荷作用點的最大撓度fmax=0.3 726 mm，代入公式中得到彎曲剛度CB=3.07×106Nm2。根據使用要求和經驗，車架在正常使用條件下，彎曲剛度應保證在前后軸中點處施加1 kN載荷時撓度值不大于0.85 mm［3］，該車架的彎曲撓度在容許撓度范圍內，車架滿足彎曲剛度要求。此車架的彎曲撓度比容許撓度小很多，彎曲剛度比較高。

2.2 扭轉剛度分析

計算車架扭轉剛度時，約束前橋在車架右縱梁上的豎直投影點的垂直位移，約束后橋在車架左縱梁上的豎直投影點的垂直位移，于后橋在車架右縱梁上的豎直投影點處施加一垂直向上的載荷，讓車架產生純扭轉變形，車架扭轉剛度的邊界條件如圖5所示。

車架的扭轉剛度計算公式如下：

式中：CT為扭轉剛度（Nm/°）；F 為集中載荷（N）；L 為力臂（m）；h 為撓度（m）。

當F=1 000 N時，車架的變形結果如圖6所示。車架載荷作用點的最大撓度hmax=8.822 mm，根據公式得車架的扭轉剛度CT=1 432 Nm/°。對比相關文獻，本車架的扭轉剛度比較高。這也從有限元計算的角度說明了帶有副車架的雙層車架的彎曲與扭轉剛度比較大。

3 模態分析

3.1 車架自由模態計算

模態分析就是確定結構的振動特性，得到其固有頻率和振型的過程，它是有限元動態分析的核心。結構的低階振型對結構的動態影響程度比高階振型大，因此，低階振型決定了結構的動態特性。在對車架進行模態分析時，由于車架結構的模態參數只與自身的結構有關，與外部載荷及約束條件關系不大，故在計算時不考慮外部載荷和邊界條件，不施加任何 載 荷 和 約 束 ， 使 其 處 于 自 由 狀 態［4］。 利 用HyperWorks自帶的OptiStruct求解器求解車架的前6階自由模態，得到車架的前六階固有頻率及振型。車架的前六階固有頻率見表1，其振型見圖7（注：振型圖放大50倍）。

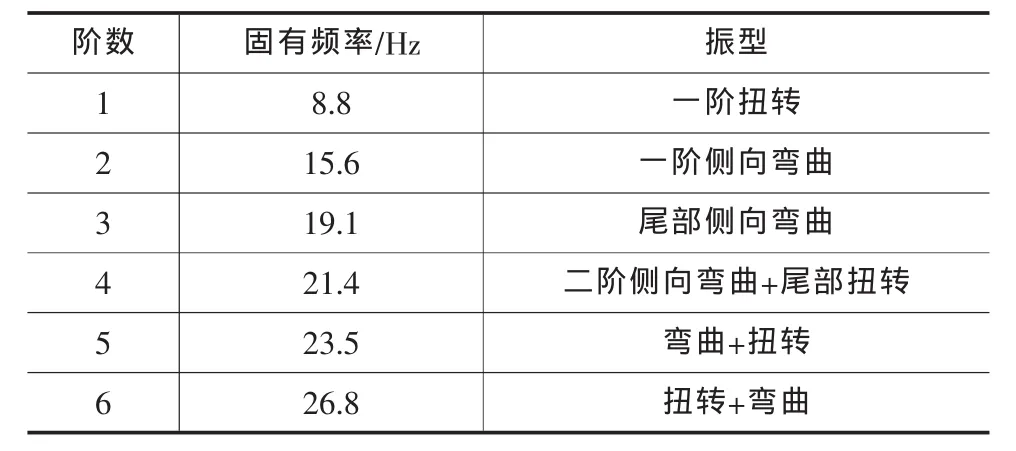
表1 車架前六階固有頻率與振型

由表1以及圖7可見，此車架的低階固有頻率分布比較均勻，振型比較合理，振動變形多發生在尾部。尾部之所以變形較大，是因為此車架尾部的行李托架為一懸臂梁結構，而這種結構在工程中是較易發生振動變形的。除尾部外，振動變形均較小，振型比較光滑，車架的結構比較穩定，反映出該車架具有較好的動態特性。

3.2 車架整體模態評價

車輛在正常行駛中所受激勵主要包括路面激勵、發動機激勵、車輪不平衡激勵及傳動軸激勵。當這些激振頻率與車架的某一固有頻率相吻合時就會產生共振。因此要求車架低階頻率（即一階扭轉和彎曲頻率）避開這些激振頻率，以避免發生整體共振［4］。

道路激勵頻率一般小于3 Hz；車輪不平衡激勵一般小于5 Hz；公交車車速在40～70 km/h時，傳動軸激勵在30 Hz以上；而發動機的振動頻率隨著發動機轉速的變化而不同，可以通過以下公式計算發動機的振動頻率：

本客車采用的是六缸四沖程發動機，怠速轉速一般600 r/min，由公式計算可得該發動機怠速時的振動頻率為30 Hz。而在正常行駛時發動機的激振頻率遠高于怠速時的振動頻率。

由模態分析的計算結果，車架的前六階固有頻率在8.8～26.8 Hz之間，通過比較，其低階頻率避開了車輛在正常行駛中所受主要激勵的激振頻率，因此車架不會與整車發生共振。可見該車架滿足動態特性的條件，符合車架設計要求。

4 尺寸優化及結果分析

車架結構優化的同時，必須考慮到車架的剛度和模態性能，這兩個指標反映了車架結構最基本的靜動態特性。此處的優化要求優化后車架的剛度不低于優化前車架的剛度，同時希望模態特性也盡量不要有變化。

目標函數：優化的目的是使車架總質量盡可能低，因此以車架體積最小為目標。

約束：由于希望優化后車架的彎曲、扭轉剛度不低于原車架的彎曲、扭轉剛度，模態一階扭轉頻率也盡量不要變化太大。于是限定彎曲工況下的最大撓度不大于0.372 6，扭轉工況下的最大撓度不大于8.822，模態一階頻率范圍設定為8～10 Hz。

設計變量：車架的彎曲振動主要受其縱梁的影響，扭轉振動主要受其橫梁的影響［5］，故重點選取車架上下共4根縱梁和14根橫梁為需要優化設計的部件。以原型車架為基礎的輕量化改型設計，需要考慮到改型設計的實際可操作性和由此帶來的加工制造成本增加，因此要盡量不改變車架的原始結構，所以這里僅以車架橫梁和縱梁的厚度作為設計變量［6］。

優化經過4次迭代達到收斂，優化的定義和優化前后零件的厚度變化見表2。目標函數隨迭代收斂情況如圖8。

由于工程上對板厚有一定規定，故將優化結果圓整，圓整后重新計算，可得整車主要性能的變化，如表3所示。

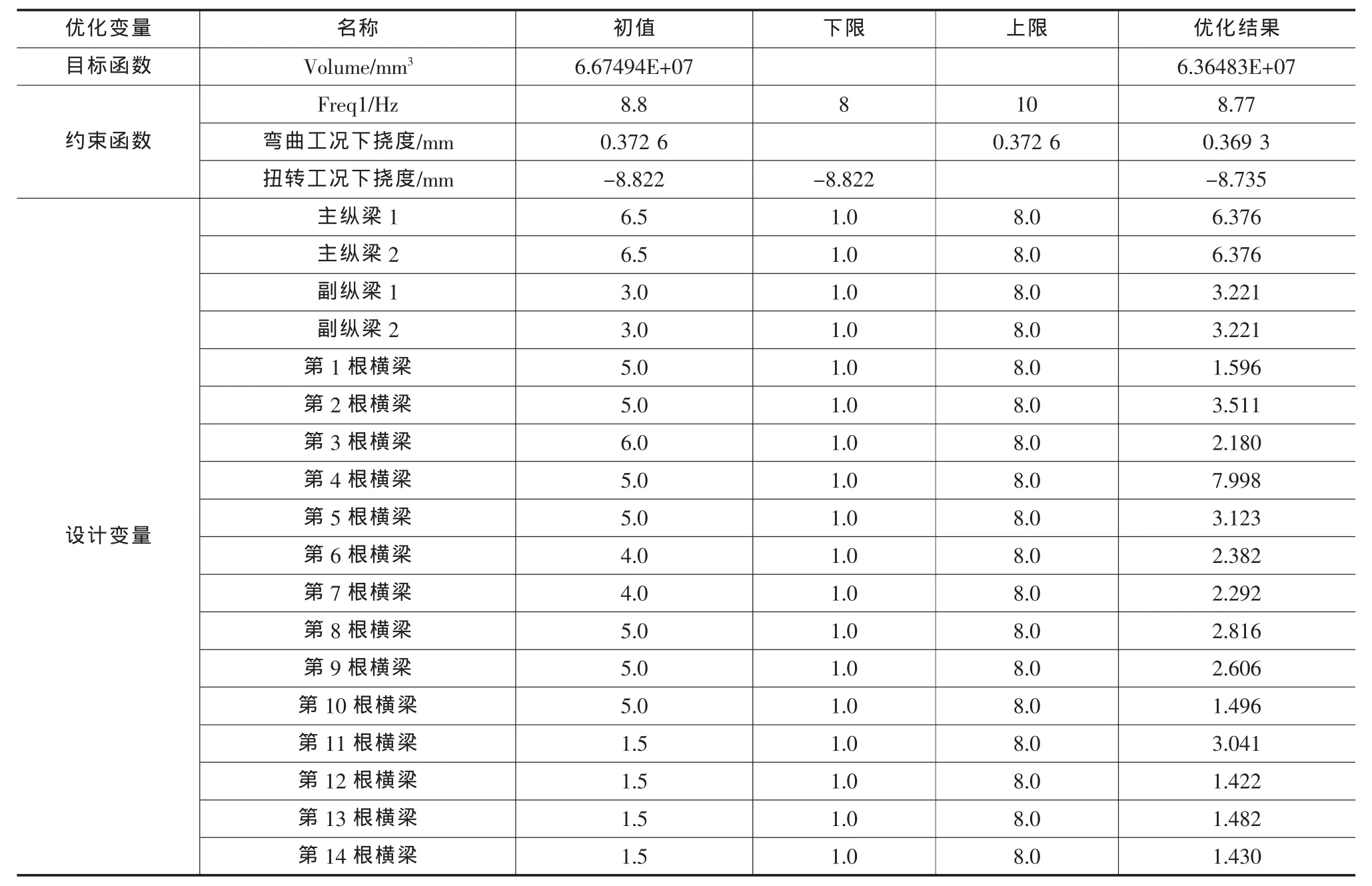
表2 優化的定義與優化結果

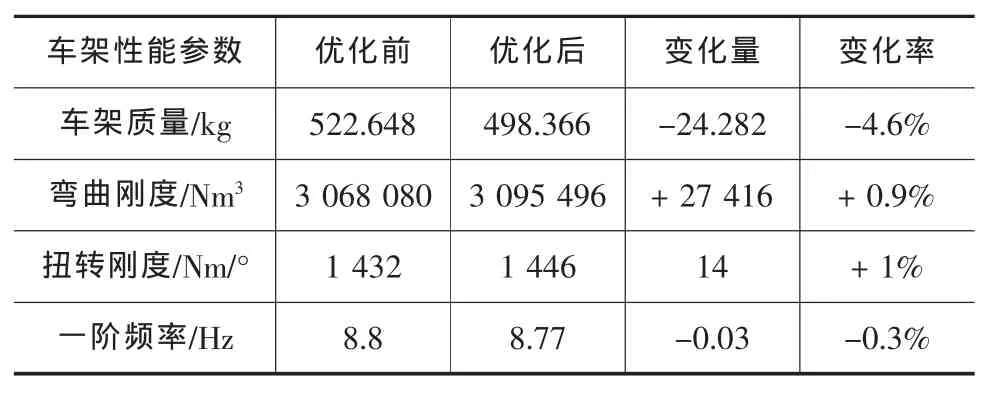
表3 優化前后車架主要性能對比

由表3可知，優化后車架質量減少了24.282 kg，下降了4.6%；在質量減少的同時車架的彎曲、扭轉剛度均有少許提高，彎曲剛度提高了0.9%，扭轉剛度提高了1%；自由模態一階扭轉頻率基本沒變。綜合看來，該優化方案是可取的。

5 結論

（1）該車架的彎曲、扭轉剛度均較一般客車車架高，說明帶有副車架的雙層車架的彎曲與扭轉剛度比較大。

（2）此種基于剛度和模態的優化方法在保證車架剛度增大且模態一階頻率基本不變的情況下實現了車架的輕量化，說明了該優化方法的合理性和可適用性。

［1］周云郊.基于剛度與模態分析的客車結構輕量化研究［J］.機械設計與制造，2010，（7）：117-119.

［2］馬迅，盛勇生.車架剛度及模態的有限元分析與優化［J］.客車技術與研究，2004，（4）：8-11.

［3］ 過學迅，鄧亞東.汽車設計［M］.北京：人民交通出版社，2005.

［4］ 柏林.載貨車車架的模態分析及優化［J］.汽車科技，2010，（4）：56-59.

［5］梅瑋，謝世坤.輕型載貨汽車變梁式車架的模態分析［J］.機電產品開發與創新，2005，Vol.18，No.2：69-73.

［6］韓旭，朱平.基于剛度和模態性能的轎車車身輕量化研究［J］.汽車工程，2007，Vol.29，No.7：545-548.