帶線性紅利的非齊次復合Poisson風險模型
韓孟云
(河海大學理學院,南京 200098)
風險理論是當前精算學界和數學界研究的熱門課題。自古典的風險模型被提出后,許多研究人員對此進行了推廣,以使其更符合保險公司的實際經營情況。但很多研究只考慮了索賠到達的復合齊次泊松過程,并沒有考慮資金的時間價值以及投資收益等其他資金活動的影響,這具有一定的局限性。
近幾年來,大量文獻對經典風險模型進行了研究,并取得了有關破產概率方面的結果[1-3]。經典風險模型是假設保險公司按照單位時間常數速率(每張保單的保費為常數c),但任何風險事業都是在隨機環境中進行的,因此,保費收取過程應是一隨機過程。文獻[4-6]利用Poisson過程對此進行了研究,文獻[7]又把線性紅利因素引入了風險模型。本文在文獻[7]的基礎上把索賠過程推廣為非齊次復合泊松風險模型,使得模型更貼近實際。
1 模型的建立
定義1 設 u≥0,給定概率空間(Ω,F,P),t≥0。令

對模型(1)作如下假設:
1){Xi,i≥1},{Yj,j≥1}是均值分別為 λ,μ 的非負獨立同分布隨機變量序列,其分布函數分別為F(x),H(x)。
2){M(t),t≥0},{N(t),t≥0}分別是參數為 A(t)、B(t)的非齊次泊松過程。
3){Xi,i≥1},{Yj,j≥1},{M(t),t≥0},{N(t),t≥0}相互獨立。
定義2 設定一個線性紅利界限z=b+qt,其中b為初值(u≤b),q為遞增速率(0<q< λ2μ2),只要盈余在紅利界限以下,便不發放紅利,若盈余在紅利界限以上,每單位時間發放λA(t)-q的紅利,直至下一次索賠發生,于是有如下關系式:
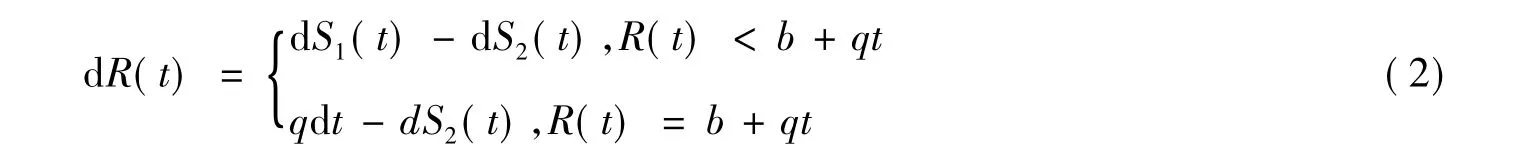
定義3 保險公司最終破產概率ψ(a,b)=P{T<∞,R(0)=u};T=min{t:t≥0且R(t)<0}表示破產概率。
定義4 令

2 主要結果
由文獻[2]中式(3.(6.3))可知,只要 ν(z,,t)滿足式(4),它便為一鞅。
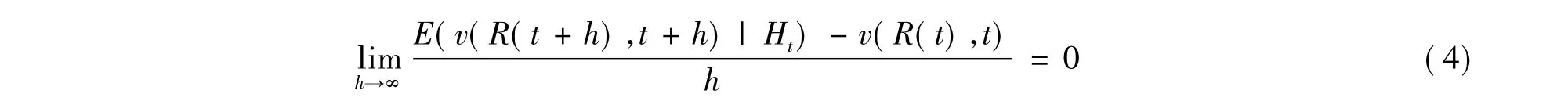
定理1 當dR(t)=dS1(t)-dS2(t)時,滿足式(5)的 ν(z,t)能使 ν(R(t),t)為一鞅。
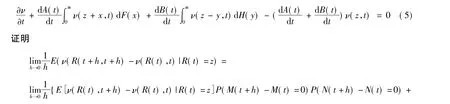
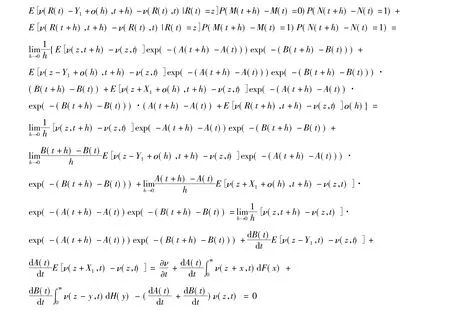
由此可知ν(R(t),t)只要滿足式(5)它便滿足式(4),就為一鞅。所以在帶線性紅利的非齊次Poisson風險模型中,要找 ν(z,t)使得 ν(R(t),t)為一鞅,ν(z,t)只要滿足:

這樣,轉而尋找這樣一個函數,使得方程(6)所有的z和t皆成立,并滿足
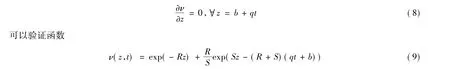
即為滿足式(6)和(8)的ν(z,t),其中R是方程
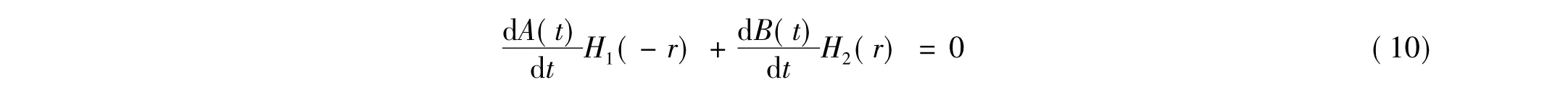
的非平凡正解,S為方程
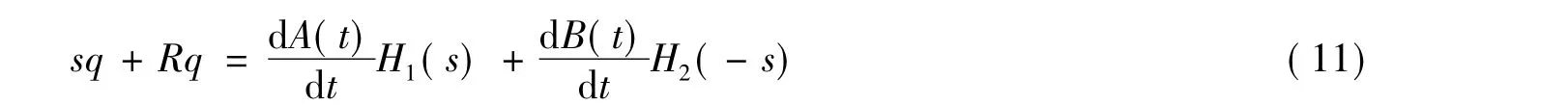
的唯一正解。
3 最終破產概率
定理2 在帶線性紅利的非齊次復合Poisson過程下的最終破產概率為
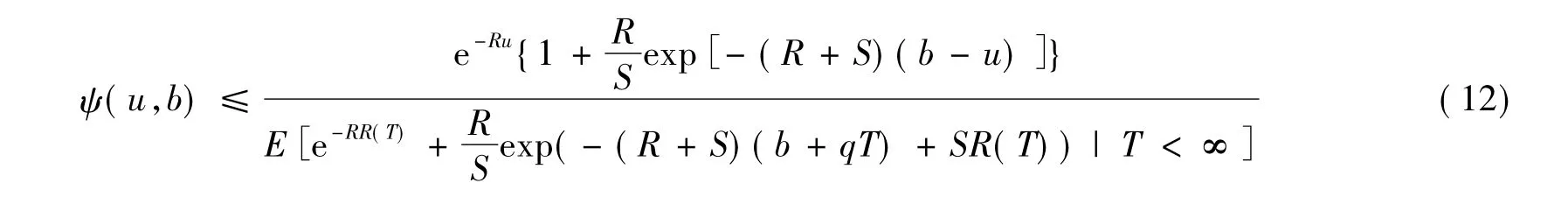
證明 假設T為破產時刻,對固定的時刻t,可證得TΛt是有界停時,利用有界停時定理知,由式(9)所確定的鞅{ν(R(t),t)}有
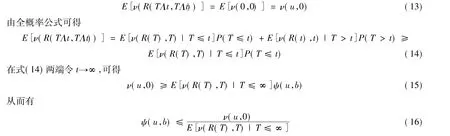
將ν代入式(16)即得到式(12),至此得出了帶線性紅利的非齊次復合Poisson風險模型的破產概率上界。
[1]GRANDEL L J.Aspects of risk theory[M].New York:Spring-Verlag,1991.
[2]GERBER H U.數學風險引論[M].成世學,嚴穎,譯.北京:世界圖書出版發行公司,1997.
[3]成世學.破產論研究綜述[J].數學進展,2002,31(5):403 -422.
[4]方世祖,羅建華.雙復合Poisson風險模型[J].純粹數學與應用數學,2006,22(2):271-278.
[5]楊善朝,馬翀,譚激揚.保費隨機收取的風險模型[J].經濟數學,2004,21(1):1-5.
[6]鐘朝艷,何樹紅,黑韶敏.古典模型的一個推廣[J].云南民族大學學報:自然科學版,2006,15(1):25-27.
[7]江五元,武坤.帶線性紅利的雙復合過程風險模型的破產概率[J].經濟數學,2005,22(3):276-278.
[8]肖碧海.幾類非齊次復合泊松風險模型的研究[D].長沙:中南大學,2006.
[9]趙金娥,王貴紅,龍瑤,等.線性紅利下帶干擾的復合Poisson風險模型[J].重慶理工大學學報:自然科學版,2010(3):115-120.

