電動客車用無刷直流電機控制系統仿真分析

牛曉玲

（西安鐵路職業技術學院 陜西 西安 710014）

隨著電力電子技術的迅速發展，無刷直流電機在電動汽車領域具有很好的應用前景[1]。目前，在研究無刷直流電機驅動純電動汽車時出現了很多建模方法。文獻[2]將無刷直流電機應用于電動汽車驅動系統，同時對無刷直流電機驅動電動汽車進行轉速-電流雙閉環控制系統仿真分析，通過仿真驗證，該控制策略可以改善了無刷直流電機的機械性能，但文中沒有融入電動汽車行駛車速。

文獻[3]通過給出無刷直流電機和電動汽車動力學數學模型，并利用傳遞函數建立了車速-電流雙閉環控制系統，同時通過仿真驗證該控制方法可獲得良好的控制效果，但在文中沒有對純電動汽車在各某檔位下的動、靜態特性進行分析。文獻[4]通過給出無刷直流電機驅動純電動汽車的數學模型，實現了機（汽車）與電（電機）的有機結合，設計了車速電流雙閉環控制策略，但在對無刷直流電機進行建模時沒有考慮到過流、欠壓和缺相等故障的保護。文獻[5]給出飛機用無刷直流電機的數學模型，并在Matlab2010a的Simulink環境下，采用S函數和模塊化建模方法，建立了相應的系統仿真模型，同時比較詳細地討論了過流、欠壓和缺相故障的保護。

在此基礎上，在Matlab7.0/Simulink環境下結合S-函數和模塊化建模方法，建立了帶有故障保護的無刷直流電機驅動純電動客車的車速閉環控制系統模型，并根據純電動客車的使用需求，對其靜、動態性能進行了驗證。仿真結果表明，車速閉環調速策略具有超調小、響應速度快、魯棒性好、自適應能力強等優點，同時驗證了帶有故障保護功能模型的合理、有效性。

1 無刷直流電機（BLDCM）的數學模型

本文以無刷直流電機的兩相導通星型三相六狀態為例，分析其數學模型及電磁轉矩特性。為了分析方便，假設磁路不飽和，不計渦流和磁滯損耗，三相繞組完全對稱。因此，根據BLDCM特性，可建立其端電壓、轉矩、狀態方程及其等效電路。

BLDCM的三相定子電壓平衡方程為[6－7]：

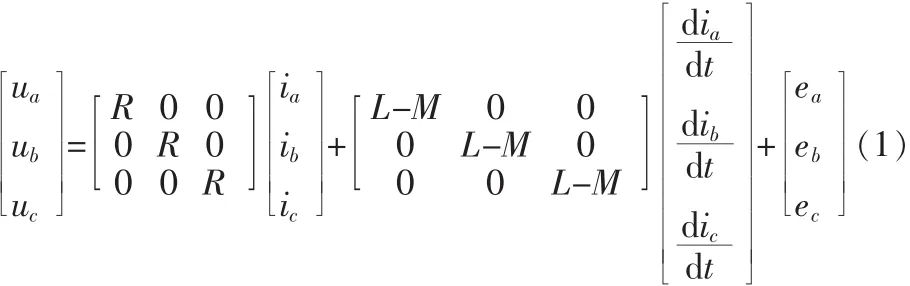
式（1）中：ua、ub、uc為定子相繞組電壓（V）；ia、ib、ic為定子相繞組電流（A）；ea、eb、ec為定子相繞組感應電動勢；L 為每相繞組的自感（H）；M為每兩相繞組間的互感（H）。

BLDCM 的 運 動 學 方 程 為[8－9]：

式（2，中：TL為負載轉矩（N·m）；J為電機轉子轉動慣量（kg·m2）；B 為阻尼系數 （N·m·s/rad），Te為電磁轉矩；ω 為電機機械角速度，Te=（eaia+ebib+ecic）/ω。

2 純電動客車數學模型

電動客車行駛時，驅動輪在不打滑的情況下，地面對驅動輪的反作用力稱為電動客車的驅動力[10]。

式（3）中，Tt為作用于驅動輪上的轉矩，r為車輪的半徑。

若用Te表示無刷直流電機轉軸輸出轉矩，ig表示變速器的傳動比，io表示主減速器的傳動比，ηT表示傳動系統的效率，則無刷直流電機軸輸出轉矩Te傳遞到驅動輪上的轉矩的關系如下所示：

電動客車的行駛方程式為[10]：

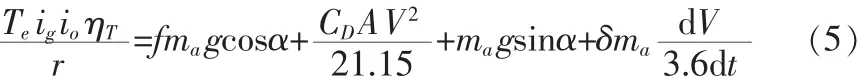
電動客車行駛時，車速與電機輸出轉速的關系為[10]：

式（6）中：n為電機轉速，單位為 r/min；r為車輪半徑，單位為m；V為車速；io為主傳動比；ig為變速器的速比。

3 基于MATLAB的無刷直流電機模塊建立

3.1 無刷直流電機系統模型

該無刷直流電動機系統由電機本體、轉子位置傳感器、控制器和電壓逆變器幾部分構成，用Matlab對無刷直流電機進行建模時主要包括電機本體、轉子位置傳感器、控制器、電壓逆變器、故障保護模塊和邏輯換相模塊，如圖1所示。

圖1 無刷直流電機系統仿真模型Fig.1 Simulation model of brushless DC motor system

根據（1）式BLDCM的三相定子電壓平衡方程，可以得到電壓平衡方程等效模型[11]，根據BLDCM的電磁轉矩可以建立轉矩計算模塊，根據BLDCM的運動學方程式可以得到轉速信號、位置信號及其電機的旋轉角速度信號如圖2所示[7]。

反電勢模塊及轉子位置傳感器模塊通過S函數來實現，根據BLDCM的轉子位置將運行周期分為6個階段[6]：0～π/3，π/3～2π/3，2π/3～π，π～4π/3，4π/3～5π/3，5π/3～2π。 因此，反電勢及轉子位置傳感器S－function為：

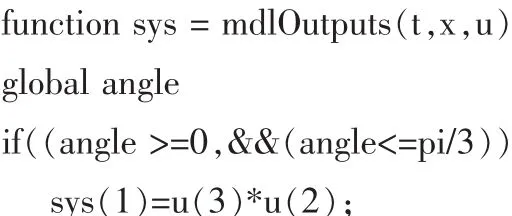
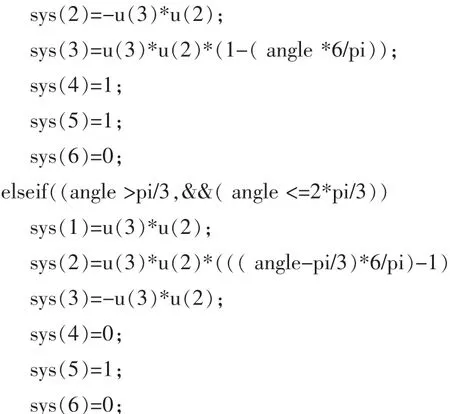
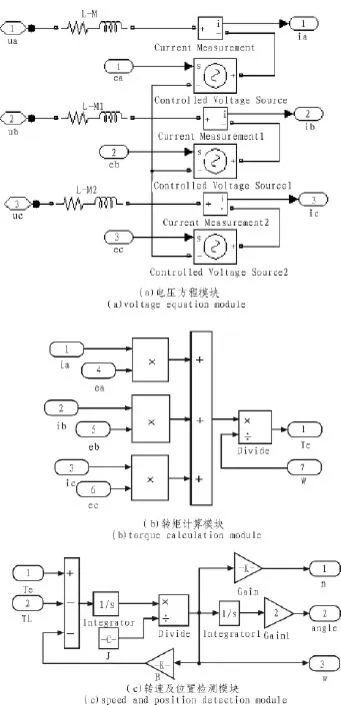
圖2 無刷直流電機系統仿真子模型Fig.2 Sub-modelofsimulationmodelofthebrushlessDCmotorsystem

邏輯換相模塊的作用是將轉子位置傳感器傳來的霍爾信號HA、HB、HC，結合控制模塊輸出的 PWM信號，轉變為相應的控制脈沖Q1～Q6，控制逆變模塊中6只開關管按特定規律導通，以產生相應的三相交流電壓供給電機本體。它們的邏輯轉換關系為[5]:

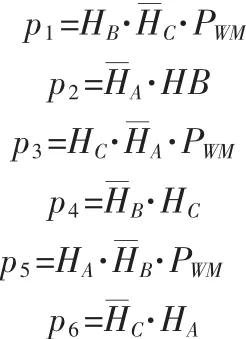
故障保護模塊包括無刷直流電機過流、欠壓及霍爾傳感器缺相等故障。無刷直流電機工作時，只要出現過流、欠壓或者缺相3種故障中的一種或幾種，保護信號就會置零，與后級的PWM波信號相與，封鎖PWM信號，從而使電機停轉，故障保護模塊如圖3所示。

3.2 純電動客車整車模型

通過式（4）、（5）可以得到純電動客車整車模型如圖4所示。

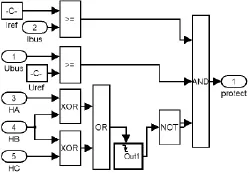
圖3 故障保護模塊Fig.3 Fault protection module

根據純電動客車部分參數及式（6），可以得到無刷直流電機驅動純電動客車驅動系統模型如圖5所示。

3.3 無刷直流電機驅動純電動客車系統模型

本文在MATLAB7.0/Simulink環境下建立了帶有故障保護功能的無刷直流電機驅動純電動客車控制系統仿真模型如圖6所示。

4 仿真結果分析

在進行無刷直流電機驅動純電動客車仿真分析時，BLDCM電機參數設置為：定子相繞組電阻R=1.5 Ω，定子相繞組自感 L=0.03 H，互感 M=-0.005 5H，轉動慣量 J=0.015 kg·m2，極對數 p=2，阻尼系數 B=0.000 15 N·m·s/rad，每相反電勢系數k=0.02，270 V直流電源供電。仿真時，所采用的試驗車輛是由某客車改裝而成，其主要參數為：主傳動比i0=6.17，車輛重量為 M=3 050 kg、變速器傳動比 ig為：5.568（1 檔）、2.832（2檔）、1.634（3 檔）、1.000（4 檔）、0.816（5 檔）、輪胎半徑 r=0.736 m、機械效率ηT=0.9。

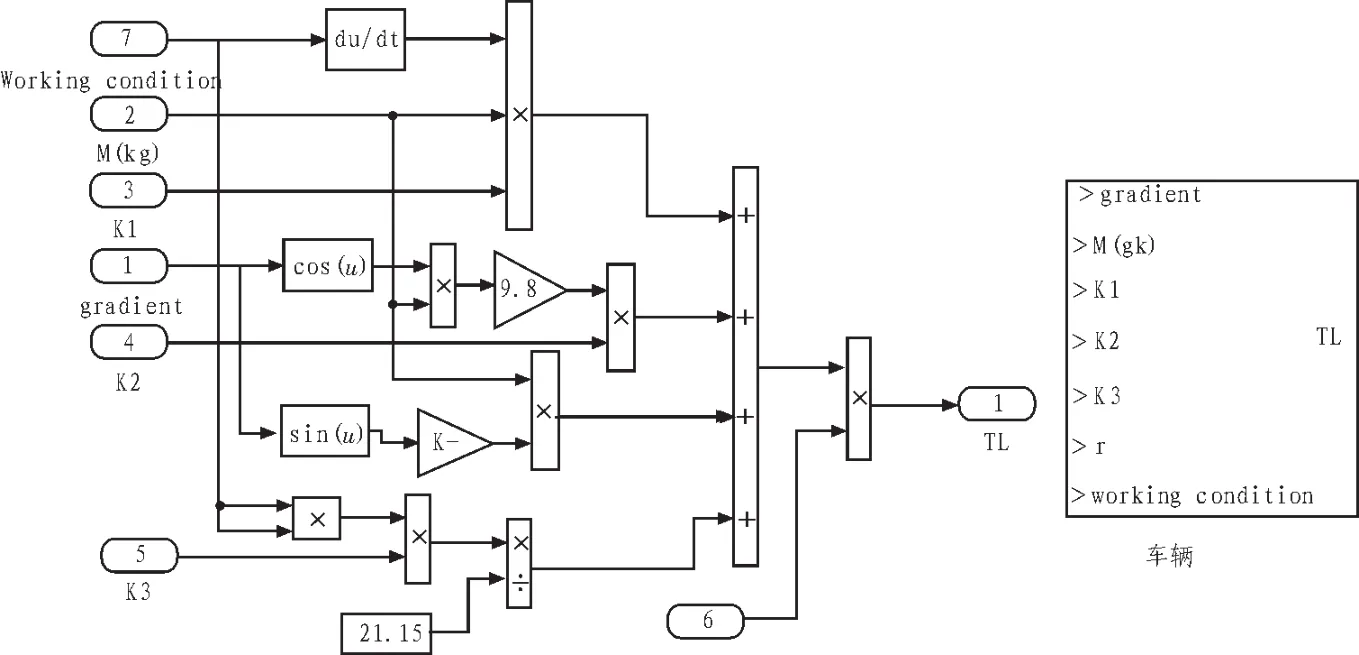
圖4 純電動客車整車模型Fig.4 Pure electric vehicle model

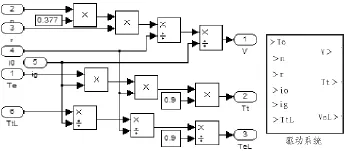
圖5 無刷直流電機驅動純電動客車驅動系統模型Fig.5 Systems model of brushless DC motor drive pure electric bus

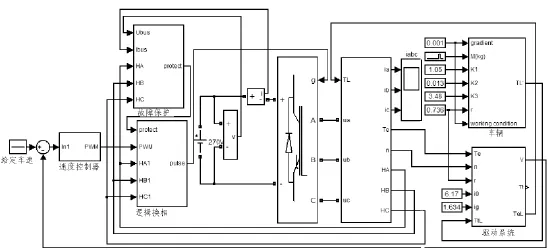
圖6 無刷直流電機驅動純電動客車整車仿真模型Fig.6 Whole simulation model of brushless DC motor drive pure electric power bus

為了驗證所設計的帶有故障保護功能的BLDCM驅動純電動客車控制系統模型的動、靜態性能，設定BLDCM允許最大電流為50 A，以純電動客車3檔位為例，設置目標車速為15 km/h，待系統進入穩態后，在t=1 s處突加負載質量M=800 kg，并在t=1.5 s時突然撤去負載。可以得到該系統中純電動客車車速、無刷直流電機轉矩、無刷直流電機轉速、無刷直流電機單相電流、三相反電勢轉矩仿真曲線。

通過上述仿真波形可以看出，純電動客車在給定的車速下，設定BLDCM的最大通過電流為50 A，通過仿真可以得到純電動客車系統整體響應快速平穩，相電流與反電勢波形與理論分析一致。同時對各故障保護功能均進行了仿真驗證，證明了本文所建立的帶有故障保護功能的純電動客車用無刷直流電動機仿真模型的有效性。當突加負載時，無刷直流電機轉速、純電動客車車速發生突降，但能馬上恢復到平衡狀態，但能馬上恢復到平衡狀態，穩態運行時無靜差，具有較強的魯棒性和抗干擾能力。

5 結 論

本文在分析無刷直流電機、純電動客車數學模型的基礎上，在Matlab7.0/Simulink環境下結合S-函數，建立了帶有故障保護功能的無刷直流電機驅動純電動客車的控制系統模型，并對控制策略進行了靜、動態性能仿真驗證。仿真結果表明：該控制系統魯棒性好、自適應能力強，同時驗證了帶有故障保護功能模型的有效性，為無刷直流電機驅動純電動客車系統仿真提供了新的方法。

[1]陳清泉，孫逢春，祝嘉光.現代電動汽車技術[M].北京:北京理工大學出版社，2002.

[2]衛國愛，全書海，朱忠尼.電動汽車驅動用無刷直流電動機的控制與仿真[J].電機與控制應用，2009，36（1）:16-19，31.

WEI Guo-ai，QUAN Shu-hai，ZHU Zhong-ni.Simulation and control of brushless DC motor in electric vehicle drives[J].Electric Machines& Control Application，2009，36 （1）:16-19，31.

[3]汪貴平，馬建，楊盼盼，等.電動汽車起步加速過程的動力學建模與仿真 [J].長安大學學報：自然科學版，2009，29（6）:98-102.

WANG Gui-ping，MA Jian，YANG Pan-pan，et al.Dynamic modeling and simulation of starting and acceleration for electric vehicle[J].Journal of Chang’an University：Natural Science Edition，2009，29（6）:98-102.

[4]張亞軍.雙能量源純電動汽車驅動與再生制動控制策略研究[D].西安:長安大學，2011.

[5]馬銀龍，尹航，柯棟梁.飛機用無刷直流電動機系統仿真分析[J].微特電機， 2011（9）:10-12， 33.

MA Yin-long，YI Hang，KE Dong-liang.Simulation analysis of brushless DC motors for aircraft[J].Small& Special Electrical Machines，2011（9）:10-12，33.

[6]Xiao X，Li Y，Zhang M，et al.A novel control strategy for brushless DC motor drive with low torque ripples[J].IEEE，2005（5）:1660-1664.

[7]紀志成，沈艷霞，姜建國.基于Matlab無刷直流電機系統仿真建模的新方法[J].系統仿真學報，2003，15（12）:1745-1749.

JI Zhi-cheng，SHEN Yan-xia，JIANG Jian-guo.A novel method for modeling and simulation of BLDC system based on matlab[J].Journal of System Simulation，2003，15（12）:1745-1749.

[8]Bharatkar S S，Yanamshetti R，Chatterjee D，et al.Reduction of commutation torque ripple in a brushless DC motor drive[C]//IEEE International Conference on Power and Energy，2008（8）:289-294.

[9]王永益，龐全，王家軍.基于網絡的無刷直流電動機控制系統的研究[J].微特電機，2009（1）:42-43.

WANG Yong-yi，PANG Quan，WANG Jia-jun.Research of brushless DC motor control system based on network[J].Small&Special Electrical Machines，2009（1）:42-43.

[10]余志生.汽車理論[M].5版.北京:機械工業出版社，2009.

[11]齊蓉，周素瑩，林輝，等.無刷直流電機PWM調制方式與轉矩脈動關系研究[J].微電機，2006，39（1）:58-61.

QIRong，ZHOU Su-ying，LIN Hui，etal.The relation between torque ripples and PWM modes of brushless DC motor[J].Micro Motors，2006，39（1）:58-61.