載人登月軌道設計方法及其約束條件概述

鄭愛武 ，周建平

（1.北京航天飛行控制中心航天飛行動力學技術重點實驗室，北京100094；

2.中國載人航天工程辦公室，北京100720；3.北京航空航天大學宇航學院，北京100083）

1 引言

月球獨特的空間位置、極具潛力的科學探索前景和豐富的可利用資源，決定了月球探測活動是當今世界航天領域中極具挑戰性和顯示度的領域之一。上個世紀50年代末以來，以美國和前蘇聯為首的世界航天大國開展了大量月球探測活動，取得了一系列成果，并帶動了相關領域科技與應用的快速發展。在1959年到1976年的第一次探月高潮中，美國成功實施了6次載人登月，前蘇聯成功實施了2次無人月面自動巡視探測和3次無人采樣返回任務。20世紀90年代開始，美國、俄羅斯、印度、日本和歐空局等主要航天國家和組織紛紛提出了新的月球與深空探測計劃。美國登月的側重點是資源方面，最終目的是火星，所以把月球當成中間站；歐洲的側重點是技術，正在研究探月和登月的新方法和新技術；印度和日本的側重點則是關于月球科學的研究。

在月球探測任務中，軌道的設計問題是所面臨的一個最基本的問題，其設計的優劣直接影響任務執行的效果、甚至成敗。近年來國內在載人登月軌道設計方面已取得了一些進展。劉興隆基于圓錐曲線拼接法，從幾何與力學角度對自由返回軌道進行了分析[1]。白玉鑄等人應用分段受攝的高精度動力學模型，設計了搜索變量、約束條件與微分修正搜索算法，搜索得到了自由返回軌道和混合軌道[2]。黃文德等人給出了基于雙二體假設的軌道初步設計，對自由返回軌道的飛行時間、軌道傾角、近月距和軌道拼接點分布等參數進行特性分析[3]，并在雙二體假設的基礎上，考慮月球運動的非圓性，給出了混合軌道的設計實例，對混合軌道的特性進行了分析[4]。黃文德、陳海萍和郗曉寧等人還針對混合軌道的中止需求，在雙二體的假設下，建立了直接中止、多脈沖中止和借助自由返回軌道中止等三種中止方式的軌道計算模型。并分析了任務中止方式、中止軌道在能量需求和返回飛行時間等方面的特性[5-6]。

國外載人登月各個階段積累的成功經驗和失敗教訓，可以為我國實施載人登月計劃提供思路和啟發。本文總結了國內外載人登月軌道設計的方法以及相關的研究成果，重點概述了載人登月的軌道類型、設計方法、約束條件、優化原則和飛行模式。

2 載人登月的軌道類型

根據Apollo載人登月的成功經驗，為保證航天員的安全，用于載人登月的軌道主要有兩種類型：自由返回軌道和混合（Hybrid）軌道。自由返回軌道已被美國應用在Apollo 8，10，11任務中，從Apollo 12開始的后續任務，包括Apollo 13在內，采用的是混合軌道[7-8]。

2.1 自由返回軌道

自由返回軌道是載人登月任務首選的一類轉移軌道，也是載人登月軌道設計的基礎。如圖1所示，載人飛船只在地月轉移軌道入軌點（TLI）進行一次變軌，其后不加機動或略加修正，飛抵近月點后在引力作用下繞過月球并自動返回地球附近。Apollo首選的自由返回軌道是一條近月點高度大約為60海里（111km）的軌道。

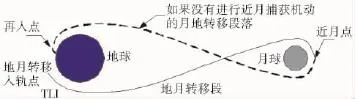
圖1 自由返回軌道示意圖

自由返回軌道的安全性高，如果航天員或飛船出現意外無法完成登月任務，那么這種軌道可以在不實施近月點制動情況下使飛船自動沿預先設計的軌道返回地球，從而挽救航天員的生命。但自由返回軌道的傾角有限，相對月球赤道面的傾角在大約10°以內，因此著陸點也限制在月球赤道附近。

2.2 混合軌道

混合軌道由自由返回軌道與非自由返回軌道組合而成，如圖2所示。

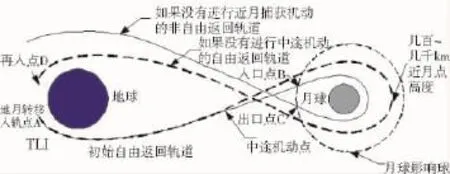
圖2 混合軌道示意圖

混合軌道在實施TLI后先進入一條自由返回軌道，該軌道的近月點高度有可能很高，從60海里（111km）到幾千海里。大約在TLI后一天（通常在半途之前），航天器進行一次機動，進入一條近月點高度大約為60海里的轉移軌道，理論上該軌道不再是自由返回的。在Apollo計劃中根據預期的誤差傳播，該軌道可以通過機動修正為自由返回模式，但修正的時機有限，一旦進入月球影響球，僅通過服務艙反應控制系統（SMRCS，推力很小，通常只用來進行中途修正[9]）完成不了軌道修正任務，此時可利用登月艙下降推力系統（LM DPS）替代SMRCS進行修正。因此，混合軌道設計還需要綜合考慮任務中止軌道設計的要求。

由于混合軌道月球軌道入軌（LOI）所需的燃料比自由返回軌道少，因此可達月球的范圍更寬。通常，混合軌道可達到的傾角從大約0°～15°（低能量）或者0°～30°（高能量）。Apollo計劃中，實施登月的Apollo 11-Apollo 17（除去未成功登月的Apollo 13）對月表的探測范圍都在南北緯30°之間。

在以下情況下將選擇混合模式而不是自由返回模式：

（1）當自由返回模式需要過多的燃料時；

（2）當自由返回模式到達月球的時間與一些限制條件發生沖突時（例如月球光照條件或特定地面站的覆蓋范圍）。

2.3 任務中止軌道

任務中止軌道不屬于正常的軌道類型，而是為了保障航天員的安全，必須考慮在飛行過程中任一點出現故障時，都能使航天員安全返回地球的應急軌道。自由返回軌道具有很高的安全性，混合軌道除了自由返回軌道段具有自主返回的能力外，其它飛行段不具備自主返回的能力，因此，在設計時，必須同時考慮任務中止軌道的設計。實踐表明，“阿波羅”計劃的順利實施與前期進行的任務中止軌道研究密不可分。在Apollo 13任務中，飛船在氧氣罐爆炸后不能使用服務艙推進系統的情況下成功返回了地球[10]。

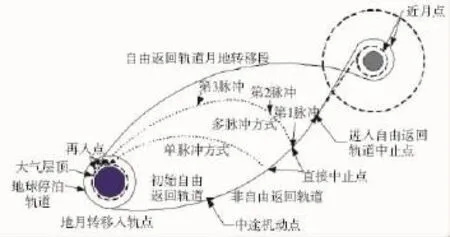
圖3 混合軌道中止方式

如果故障發生在混合軌道的非自由返回軌道段，一般可以有兩類中止方式：一類是借助自由返回軌道返回，飛船經歷一次繞月飛行后返回地球；另一類是直接進入返回地球的軌道，也就是直接中止方式。直接中止方式中，根據變軌的方法，又可分為單脈沖方式和多脈沖方式。兩種中止返回方式如圖4、圖5所示。

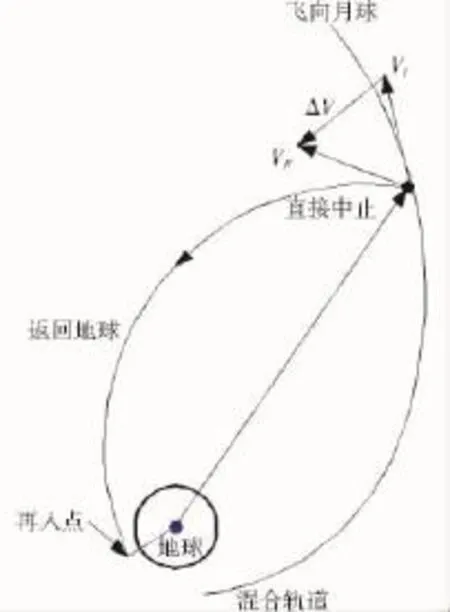
圖4 單脈沖直接中止方式

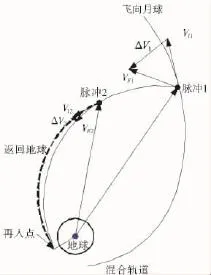
圖5 雙脈沖直接中止方式

自由返回軌道是在推進系統失效的情況下飛船能安全返回的最優軌道。對于給定中止點，設計中止自由返回軌道的方法與正常飛行的條件下自由返回軌道的設計并無本質區別，這里不再贅述。

在混合軌道的不同點位上，實現直接中止所需的能量不同。由于飛船所能提供的能量有限，在某些區域內，實現單脈沖返回是不可能的[11]。而有些區域，具有充足的能量用于返回，即能量過剩。因此，需要通過能量的優化，對于不能實現單脈沖中止的區域，利用多脈沖實現中止返回；對于能量過剩的區域，一方面，可以通過利用過剩的能量獲取高能返回軌道，減少返回時間；另一方面，可以利用過剩的能量對返回軌道進行修正，使返回軌道末端處于再入走廊（由飛行航跡角決定）的中心地帶，提高返回精度和安全系數。

3 載人登月軌道設計方法

在過去幾十年的人類探測月球的活動中，各國的研究人員研究、發展出了多種轉移軌道的設計技術，如脈沖轉移方式、連續推力轉移方式和基于弱穩定邊界（WSB）的轉移方式。不同轉移方式需消耗能量的多少和轉移時間的長短大不相同。

上世紀60～80年代期間所有的月球探測任務幾乎都采用了經典的基于Hohman轉移的直接轉移方式，比如Luna和Apollo任務。典型的直接轉移通常需要2d～5d。航天器應選擇在當月球赤緯小于停泊軌道傾角（通常等于發射場的緯度）的時候發射[12]。九十年代提出了“返回月球”計劃后，在軌道設計上有了更多的變化，采用了一些新的轉移軌道設計方法來降低ΔV的需求[13-14]。例如，日本的“飛天”號（Hiten）任務同時使用了月球借力飛行（swing-by）和WSB的軌道設計方法捕獲并進入大橢圓月球軌道。轉移時間為6個月[15]。低能軌道在對時間要求不高的無人采樣返回任務中具有廣闊的應用前景[16]。

新的低能軌道設計方法可以大大節約燃料，如Ballistic轉移比常規的Hohmann轉移大約節省15%能量[17]。而且隨著目前一些新的進展也使得飛行時間由原來的100d縮短到了13d～15d之間[18]。但對于載人登月來說，低能軌道的飛行時間還是太長，因此載人飛船的軌道設計方法還只能采用直接轉移方式。不過，未來的月球基地建設中，貨運飛船的軌道設計可以考慮更省燃料的低能軌道。

載人登月軌道設計的基本方法還是先采用簡化的動力學模型快速獲得軌道初始解，作為后續高精度軌道設計的初值，計算中采用相應的優化算法和搜索算法。直接轉移初步設計方法有Hohmann轉移、雙橢圓轉移、橢圓-雙拋物線轉移以及拼接圓錐法。這里主要介紹最常用的Hohmann轉移和拼接圓錐法。

3.1 Hohmann轉移

1925年Walter Hohmann得到了在限制性二體問題下，兩條圓軌道之間最優轉移軌道的一個解析解，該解被稱為Hohmann轉移軌道，它可以實現探測器在兩個共面圓軌道之間最小能量的轉移（R2/R1＜11.94時，R1、R2分別為兩圓軌道的半徑）。如果將月球的公轉軌道近似為圓軌道，也不考慮航天器如何被月球捕獲的問題，那么，對從地球圓軌道出發的航天器而言，Hohmann轉移是一種最便利的轉移方式。

圖6給出了利用Hohmann轉移實現地月轉移的基本過程（這里設地球停泊軌道的半徑為R1，月球停泊軌道的半徑為R2），其主要步驟為：

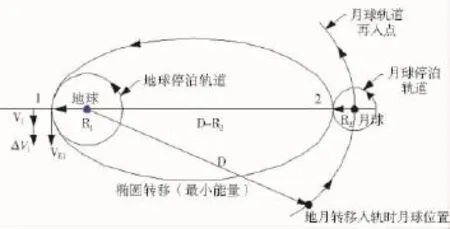
圖6 地心系下Hohmann最小能量地月轉移軌道

（1）第一步與普通的Hohmann轉移相同，就是航天器在地球停泊圓軌道上運行到“1”處時施加第一個速度脈沖ΔV1，將軌道變為繞地球的橢圓軌道，其近地點就是“1”，其遠地點位置在月球軌道附近。

由圖6可以得到轉移橢圓的半長軸amin：

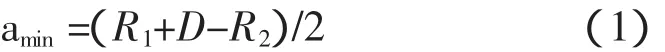
其中R1也是轉移橢圓軌道的近地點地心距 ，V1是地球停泊圓軌道上的速度，VE1是近地點的速度，VE2是遠地點的速度，D=384400 km是地月距，可以看作常數。

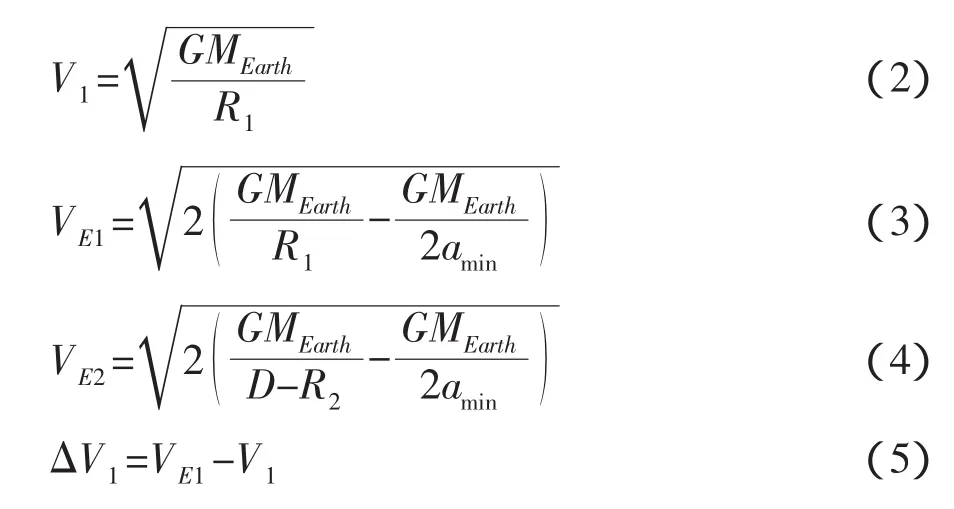
（2）第二步與普通的Hohmann轉移不相同，因為第二次脈沖不是為了使航天器進入半徑為D-R2的圓軌道而是進入月球停泊軌道，因此在轉移軌道的遠地點“2”處施加的第二個速度脈沖ΔV2與航天器的運動方向相反，如圖7所示。

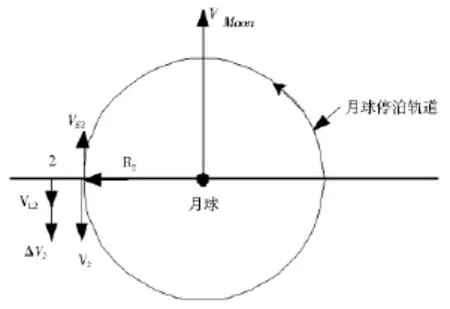
圖7 Hohmann最小能量地月轉移軌道月球段

這次制動航天器進入半徑為R2的繞月圓軌道。VL2是遠地點的速度相對月球的速度：

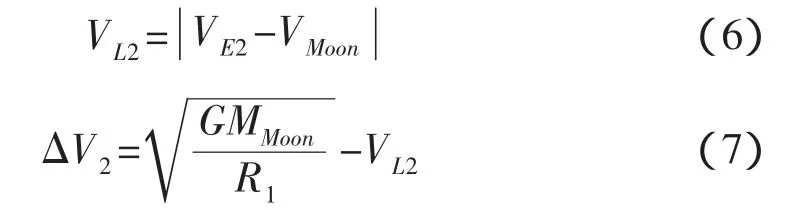
其中VMoon是月球繞地球公轉的軌道速度，MMoon為月球質量。

由于Hohmann轉移過程是在二體問題的基礎上進行的，且將月球繞地球的公轉軌道也看作圓，其所給出的轉移軌道和所需的速度增量與實際情況相差較大，因此，Hohmann轉移常被用于地月轉移軌道設計的最初階段，作為下一階段設計的初始值。

3.2 拼接圓錐曲線

拼接圓錐曲線方法是地月轉移軌道設計中經常采用的方法，計算結果的精度比Hohmann轉移高，因此可以為后續的高精度軌道設計提供更好的初值，有利于搜索算法收斂。拼接圓錐曲線法引入了月球影響球的概念，它將地月轉移軌道分成兩段，如圖8所示：地心軌道段與月心軌道段，這兩段軌道在影響球邊界上經適當拼接后形成滿足要求的飛行軌道[19]。

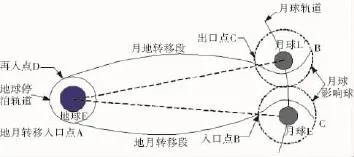
圖8 軌道拼接示意圖

圖中B點為地月轉移軌道與月球影響球的交點（即入口點），C點為航天器飛出月球影響球時與影響球的交點（即出口點）。L為入口點時刻月球的位置，L′為出口點時刻的月球位置，E為地球。AB和CD段為地心圓錐曲線，即忽略月球的影響，理論上地心段圓錐可以是橢圓、拋物線或雙曲線。但橢圓所需要的速度增量最小。BC段在月球引力場內，此時忽略地球的影響，將航天器軌道看作繞月球的Kepler軌道（一般為雙曲線軌道）。

當給定六個獨立的軌道參數：地月轉移軌道的近地距、加速點航跡角、入口點B的經、緯度、月心軌道傾角以及航天器在入口點處月心速度矢量與位置矢量反方向夾角時，可以利用解析公式求出地心軌道轉移初速、加速點地心位置矢量、入口點B的地心位置和速度矢量、入口點B的月心位置和速度矢量。由入口點B的月心位置和速度矢量，可以求得出口點C的月心位置和速度矢量。然后通過坐標轉換得到出口點C的地心位置和速度矢量。再由地心位置和速度矢量求出月地轉移軌道段在地心坐標系中的傾角和近地距。

拼接圓錐曲線方法也是基于二體問題完成的，它在最初的軌道設計中是一種很好的近似，與精確軌道設計相比，除了對軌道力模型進行了簡化（未考慮攝動力的影響）之外，兩者在其它方面都是一致的。在雙二體假設下得到的軌道，可以作為精確設計的初值，提高設計效率。不過，由于太陽引力場的干擾，以及第一段中月球引力場和第二段中地球引力場的干擾，這種近似在月球影響球部分是有顯著誤差的[19]。

3.3 高精度軌道設計

前述方法都是解析法，對軌道模型進行了簡化，也沒有考慮攝動項的影響。事實上，在地月系統的軌道設計中，攝動項的影響是非常大的。高玉東以雙二體假設下得到的一條月地轉移軌道為標稱軌道，分析了攝動因素對軌道計算精度的影響程度，如表1所示[20]。

因此，雖然解析法的計算速度快，但精度不高，都只能作為高精度軌道設計的初值。高精度軌道設計還是需要基于高精度的軌道模型采用數值法積分。在開始軌道設計之前，需要綜合考慮軌道設計的各種約束條件，尋求各種約束條件的平衡。

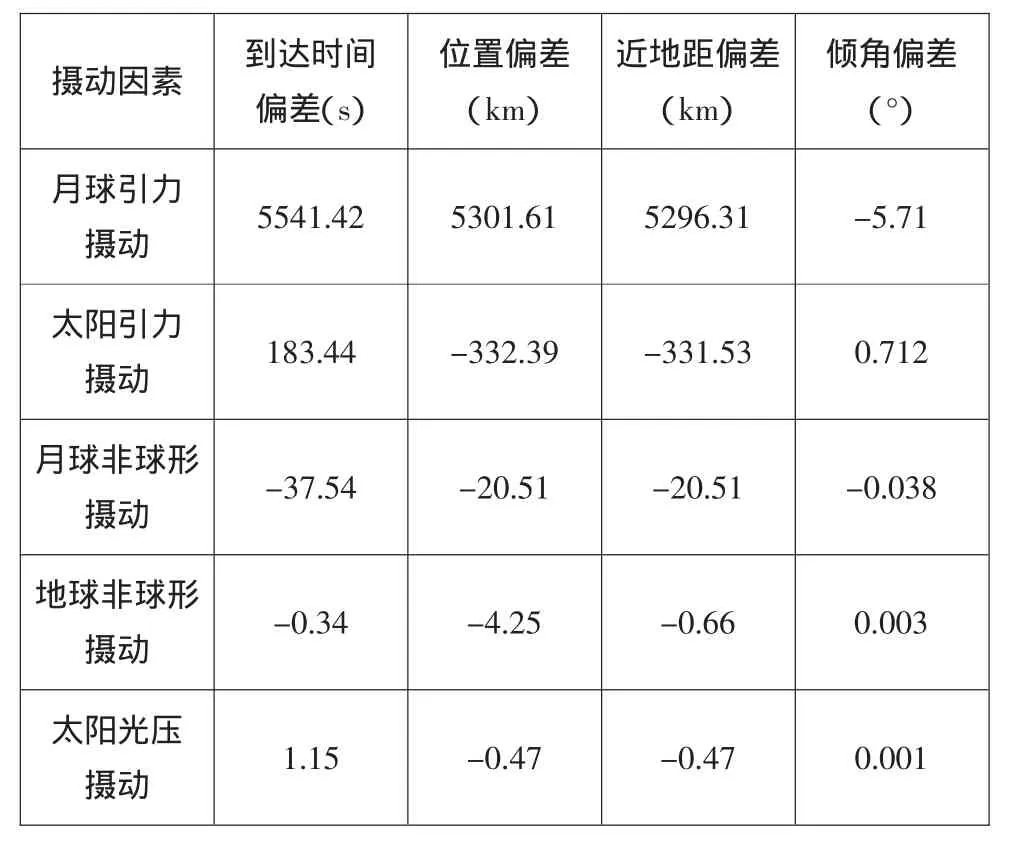
表1 各項攝動因素對月地轉移軌道近地點時刻參數的影響

3.3.1 載人登月軌道設計的約束條件

參考Apollo11任務，在正常的載人登月軌道設計中需要考慮的約束條件包括[7]：運載火箭運載能力、發射窗口要求、發射場經緯度及發射方位角限制、入軌精度要求、航天器燃料量和航天器的推力系統和推力大小、月球著陸點的選擇、月球著陸時的光照角要求、地球著陸時的光照角要求、測控覆蓋范圍、航天器軌道壽命或最長運行時間、航天器發熱極限、航天器能否過月夜的能力、航天器過載限制、最大再入速度和再入走廊、著陸場選擇、落點精度要求和飛行時間等等。如果航天器由使用運載火箭直接送入地月轉移軌道，則發射方案和運載火箭決定了轉移軌道的近地點高度和轉移軌道傾角。

任務中止軌道設計也受到多方面的約束，包括：再入走廊、可使用的速度增量大小、返回時間、著陸區域、發射窗口、返回著陸時刻等[21]。再入走廊約束是任務中止軌道設計的最基本約束，無論以什么方式返回都必須滿足。速度增量約束和返回時間約束是最主要的約束。如當飛船的推力系統出現故障時，可利用的速度增量有限，以最小速度增量返回就是最主要的目標。而當飛船上的生保用品不足或設備故障可能危及到航天員生命時，以最少時間返回又成了最重要的要求。這兩個約束是相互矛盾的。當用最小速度增量返回時，所耗費的時間必然就長，而考慮最少時間返回時，所需要的速度增量也最大。通常要將最小速度增量和最少時間進行折衷，使任務中止軌道達到最優性能。如果在某個時刻進行任務中止的最小速度增量仍然超過了飛船現存推力系統的能力，那么在這個時刻就不能進行任務中止機動。這樣就存在一個任務中止的可行性區間的問題。在可行區間內，可以直接進行任務中止，否則就必須等飛船進入可行區間后才能進行任務中止。

3.3.2 高精度動力學模型

通常情況下，在地月空間內運動的航天器受力包括：地心引力與月心引力、地球與月球非球形攝動、其他天體引力攝動、太陽光壓攝動、大氣阻力攝動以及地球潮汐攝動等。目前地月間最常用的動力學模型還是根據月球影響球進行分段的受攝二體模型。

根據Laplace的建議，以月球為中心的影響球半徑為：

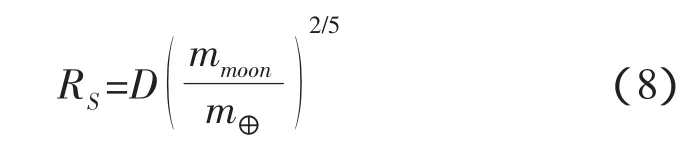
其中D為地月距，mmoon為月球質量，m⊕為地球質量。

分段受攝高精度動力學模型分為地心段和月心段：

地心段考慮地心引力、地球非球形攝動、日月引力攝動、太陽光壓攝動與大氣阻力攝動，月球和太陽的星歷采用DE405，在理想慣性坐標系下的動力學方程如下：

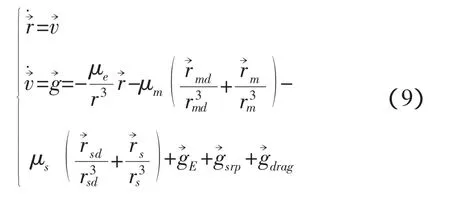
其中，μe、μm和μs分別是地球、月球和太陽的引力常數和→分別為月球、太陽和航天器相對于地心的矢徑，和分別表示航天器到月球和太陽的矢徑為地球非球形攝動，為太陽光壓攝動為大氣阻尼攝動，相應的計算公式可參見文獻[22]。

月心段（月球影響球內）考慮月心引力、月球非球形攝動、日地引力攝動與太陽光壓攝動，動力學方程如下：

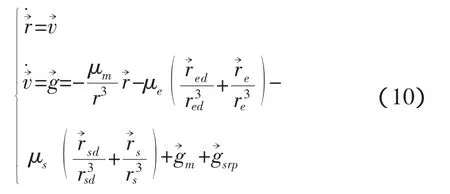
3.3.3 軌道優化原則

經典軌道設計的優化條件一般都是燃料最省原則。為了使所需能量最省，即總速度增量的模最小，需要對軌道設計過程進行優化處理。比如在自由返回軌道設計中，可以結合近月距和對月傾角等約束條件，取目標函數為：

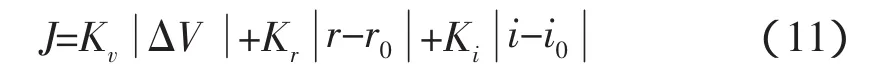
其中，r、r0分別表示實際近月距和要求達到的近月距，i、i0分別表示實際相對月球的軌道傾角和要求達到的軌道傾角。Kv、Kr和Ki為常數系數，分別用于調整三者之間的權重。于是，可以建立滿足約束條件的最優化問題，應用最優化方法進行求解，得到滿足約束條件的軌道。

一旦航天器發射升空，確保任務成功就是遠比節省燃料更重要的問題了，特別是在任務發生故障或進入應急的情況下，因此軌道設計的優化條件也需要進行調整。在故障和應急情況下以燃料最省為原則沒有意義。機動后沒有使用的燃料最終也會被拋棄或返回地球。所以，在故障和應急情況下，主要是將可用的燃料作為一個限制條件而不是優化條件，對使任務更有風險的其他參數進行優化，比如返回時間，機動次數，或再入速度[23]。總而言之，主要目標是減少機動次數，其次是使飛行時間最短。

3.3.4 載人登月的飛行模式

載人登月的軌道設計還與載人登月的飛行模式緊密相關。優化載人登月的飛行模式，可以合理規劃登月模塊數量、規模和總體方案，明確火箭運載能力需求、發射次數，降低載人登月工程的研發難度，縮短研制周期，提高載人登月大系統工程的可靠性，節省研制經費。Apollo采用了單次發射（人貨混運）+月球軌道交會（Lunar Orbit Rendezvous，LOR）返回登月模式，星座計劃選用兩次發射（人貨分離）地球軌道交會（Earth Orbit Rendezvous，EOR）+LOR 返回登月模式，歐洲提出了四次發射，3次EOR+LOR返回登月模式。由于缺少超重型運載火箭，俄羅斯能源公司載人登月方案采取運載火箭7次發射，EOR（5次），+1次LOR返回登月的飛行模式[24]。盛英華等人基于載人登月飛行模式、飛行模塊質量、可靠性和研制難度的分析，初步研究認為兩次發射EOR+LOR返回登月模式是我國載人登月工程的較佳路線，但目前運載能力無法滿足需求[25]。因此，較好的方案是三次發射（人貨分離），兩次EOR+LOR返回登月模式。

4 結束語

總的來說，國內關于載人登月軌道設計考慮的約束條件都還比較簡單，比如僅考慮了近月點高度和環月軌道傾角，對月面著陸點位置、發射窗口、軌道兩端的光照條件和地面測控等約束條件還需要進一步進行研究。

載人登月工程是一項技術含量高、復雜度大的大科學工程，具有極高的風險性。國外載人登月研究和實踐積累的成功經驗和失敗教訓，值得我們跟蹤和研究，為我國實施載人登月計劃提供思路和啟發。本文總結了國內外載人登月軌道設計的方法以及相關的研究成果，詳細介紹了載人登月自由返回軌道、混合軌道和任務中止軌道等三種類型軌道設計的設計思想、約束條件和優化原則。希望本文的工作能為我國未來的載人登月工程的任務軌道設計以及任務中止軌道設計工作提供參考。 ◇

［1］LIU Xinglong，DUN Guangren.Designs of optimal free-return orbit for moon landing ［C］.2007 IEEE Intematioual Conference on Robotics and Biomimetics（ROBIO），Sanya，2007:936-940.

［2］白玉鑄，陳小前，李京浩.載人登月自由返回軌道與Hybrid軌道設計方法［J］.國防科技大學學報，2010，32（2），:33-39.

［3］黃文德，郗曉寧，王威，李靜.基于雙二體假設的載人登月自由返回軌道特性分析及設計［J］.宇航學報，2010，31（5）:1297-1303.

［4］黃文德，郗曉寧，王威.基于雙二體假設的載人登月混合軌道特性分析及設計［J］.國防科技大學學報，2010，32（4），61-67.

［5］黃文德，郗曉寧，王威.基于雙二體假設的載人登月中止軌道特性分析［J］.宇航學報 2010，31（9）:2067-2074.

［6］陳海萍.載人登月任務中止軌道特性分析［D］.長沙:國防科技大學，2009.

［7］Ronald L.Berry.Launch Window And Translunar，Lunar Orbit，and Transearth Trajectory Planning and Control for the Apollo 11 Lunar Landing Mission.AIAA No.70-24，AIAA 8th Aerospace Science Meeting，New York，January 19-21，1970.

［8］Adamo D R.Apollo 13 Trajectory Reconstruction via State Transition Matrices ［J］.Journal of Guidance，Control，and Dynamics.2008，31（6）:1772-1781.

［9］Anselmo D R，Baker M K.Translunar and Lunar Orbit Abort Trajectories for Apollo 14.NASA-CR-116280［R］，Bellcomm，Inc.，Dec 7，1970.

［10］Richard W O.Apollo by the Numbers:A Statistical Reference［R］.NASA SP-2000-4029，2000.

［11］Beksinski E D.Abort Trajectories for Manned Lunar Mission［D］.University of Maryland，2007.

［12］R.Biesbroek，G.Janin.Ways To The Moon.ESA bulletin 103，august 2000.

［13］V.Krish，E.A.Belbruno，andW.M.Hollister，An investigation into critical aspects of a new form of low energy lunar transfer，the Belbruno-Millertrajectories.AIAA/AAS Astrodynamics Conference （South Carolina， 1990）， American Institute of Aeronautics and Astronautics，Washington，DC，AIAA-1992-4581，1992:435–444.

［14］Koon W.S.，Lo M.W.，Marsden J.E.，et al.Low Energy Transfer to the Moon.Celestial Mechanics and Dynamical Astronomy，Kluwer Academic Publishers，Netherlands，Vol.81，2001:63-73.

［15］E.A.Belbruno and J.Miller.A ballistic lunar capture trajectory for the Japanese spacecraft hiten.Technical Report IOM 312/90.4-1731-EAB，Jet Propulsion Laboratory，Cal.Tech.，1990.

［16］ Lo， M.W.， Chung， M.J.， Lunar Sample Return via the Interplanetary Superhighway.AIAA/AAS Astrodynamics Specialist Conference，Monterey，California，Paper AIAA 2002-4718，August 2002.

［17］T.H.Sweetser.An Estimate of the Global Minimum Needed for Earth-Moon Transfer.in J.K.Soldner， A.K.Misra， 1...1..Sackett，and R.Holdaway （eds.），Spaceflight Mechanics 1991，Volume 75，Part I of Advances in the Astronautical，Sciences，pp.111-120，Univelt，San Diego，1991.

［18］Cristiano Fiorilo De Melo.Othon Cabo winter.Alternative Paths To Earth-Moon Transfer.Mathematical Problems in Engineering.Volume 2006，Article ID 34317，Pages 1～20 DOI 10.1155/MPE/2006/34317.

［19］Roger R.Rate，Donald D ，Mueller，Jerry E.White.Fundamentals of Astrodynamics［M］.Dover Publications.Inc，New York ，1971.

［20］高玉東.月球探測器地月空間轉移軌道研究［D］.長沙：國防科技大學，2008.

［21］陳海萍.載人登月任務中止軌道研究綜述［J］.太空探索，2006年11期.

［22］劉林.航天器軌道理論［M］.北京:國防工業出版社，2000.

［23］Shane B.Robinson and David K.Geller.A Simple Targeting Procedure for Lunar Trans-Earth Injection.AIAA Guidance，Navigation， and Control Conference.August 2009，Chicago，Illinois:10-13.

［24］范嵬娜.國外載人登月飛行模式特點［J］.國際太空，2011，4:56-59.

［25］盛英華，張曉東，梁建國，趙金才.載人登月飛行模式研究［J］.宇航學報，2009，30（1）:1-7.