GPS信息和限誤差信息率與信息率失真及復(fù)雜性失真之間的關(guān)系

魯晨光

（廣東方舟投資管理有限公司,廣東廣州 510610）

0 引言

文獻[1]介紹了如何推廣Shannon信息論[2]到一般領(lǐng)域,包括語義信息和感覺信息領(lǐng)域。書中介紹信息率失真的兩個新版本:限誤差信息率 R（AJ）（文中記為R（T））和保精度信息率R（G）,討論了它們和信息率失真之間的等價關(guān)系。后來又進一步討論這些問題[3-4]。現(xiàn)在,通過研究發(fā)現(xiàn)復(fù)雜性失真只是限誤差信息率的特例,復(fù)雜性理論研究者肯定的復(fù)雜性失真和信息率失真之間的一般等價關(guān)系是不成立的。文獻[1]同時介紹了如何根據(jù)人眼色覺分辨率度量色覺信息,目前,GPS提供信息以類似的方式;并且通過對GPS信息的度量,可以加深對信息率失真的理解。文中首先介紹如何度量GPS提供的信息,然后討論和數(shù)據(jù)壓縮理論相關(guān)的那些函數(shù)的等價關(guān)系,并用編碼例子說明。

1 GPS信息——從統(tǒng)計信息到預(yù)測信息

1.1 GPS精度和集合Bayes公式

全球定位系統(tǒng)（Global Positioning System,GPS）通常假設(shè)目標(biāo)實際位置以GPS讀數(shù)為中心正態(tài)分布。

假設(shè)信源是帶有GPS跟蹤器的被盜小車,為簡化起見,其位置用一維離散隨機變量X表示,實際可能位置是x1,x2,…它們構(gòu)成集合 A={x1,x2,…}。用Y表示GPS讀數(shù),Y的實際取值是y1,y2,…;它構(gòu)成集合B={y1,y2,…}。讀數(shù) yj即xj的估計,通常寫為＾xj。那么在信源等概率假設(shè)下,讀數(shù) yj出現(xiàn)時,xi發(fā)生的條件概率分布為:

其分布如圖1所示。GPS精度常見的表示法是均方根差（Root Mean Square error,RMS）表示法。DRMS=10米就表示σ=10m,目標(biāo)有68.2%的可能性在以讀數(shù)xj為中心,半徑10m的圓圈之類。2DRMS=10m就表示2σ=10m,目標(biāo)有95.44%的可能在半徑為10米的圓圈之類。常見的還有一種是圓概率誤差（CEP）表示法,CEP是10m,就表示實際位置有50%可能落在以GPS讀數(shù)為中心半徑=10m的圓圈之內(nèi)。

請注意,一般情況下,P（X）不是等概率的,條件概率P（X|yj）也不會呈正態(tài)分布。比如,汽車在公路上的先驗概率比較大,即使GPS定位小車在公路附近農(nóng)田里,那也并不意味著汽車在農(nóng)田里概率最大。要表示GPS獨立于信源的特性,最好被寫為

把上面曲線理解為 xi和xj混淆概率函數(shù)或xi和xj的相似度,其最大值等于1。而條件概率P（xi|yj）對 xi求和等于1,對于連續(xù)分布其最大值是0.399/σ。

混淆概率可以來自隨機集合的統(tǒng)計[7-8]。假設(shè)做很多次分辨實驗,每次確定一個A中子集,其中元素和 xj想混淆。做N次實驗就得到N個子集,它們的左右邊界可能不同,如果有Ni個子集包含xi,那么混淆概率就等于:

定義模糊糊集合[9]Aj={所有和 xj相混淆的xi},那么 xi在Aj上隸屬度,記為 Q（Aj|xi）,就可以用混淆概率c（xi,xj）來定義,即 Q（Aj|xi）=c（xi,xj）。

Q（Aj|xi）也可以被理解為 xi和xj的相似度,或命題yj=“X is about xj”在 xi發(fā)生時的邏輯真值或yj的后驗邏輯概率。而yj的先驗邏輯概率就是Q（Aj|xi）的平均值:

也就是Zedah曾提出的模糊事件的概率[10]。已知X在Aj中,求X的概率分布,有集合Bayesian公式[4]或廣義Bayesian公式[8]:

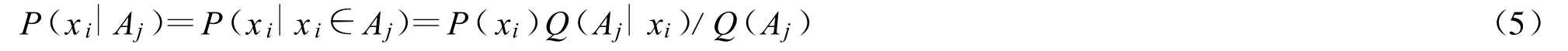
后面討論信息率失真函數(shù)和限誤差信息率函數(shù)時,將看到,上面關(guān)于Q（Aj）和P（xi|Aj）的公式一再出現(xiàn)。當(dāng)Aj是清晰集合時,P（xi|Aj）的圖解如圖3所示。

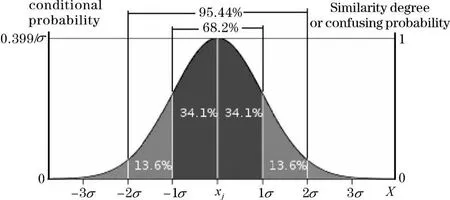
圖1 反映X和xj的混淆概率和相似度的GPS的誤差函數(shù)

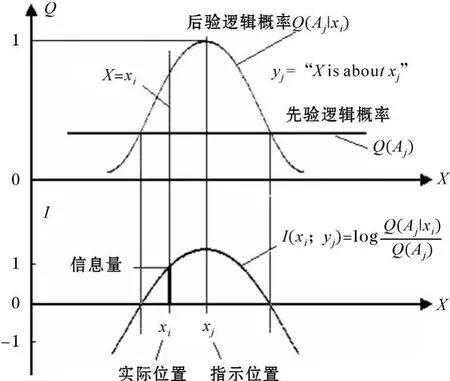
圖2 預(yù)言信息公式圖解

1.2 從統(tǒng)計信息到預(yù)言信息

要度量一個GPS讀數(shù)提供的信息,用Shannon熵 H（X）公式或Shannon互信息 I（X;Y）公式都是不行的。因為它們是用來度量平均信息的[2]。為此,提出用Shannon互信息公式中的對數(shù)部分度量單個事件提供的信息[11],公式是:

但是這個公式能導(dǎo)致負的信息（當(dāng)P（xi|yj）＜（P（xi）時）,所以很多人對此有疑問。

接受這個公式,是因為負信息可以理解為因謊言或錯誤預(yù)測而增加的編碼長度。但是,度量GPS信息還要考慮事實檢驗,因為根據(jù)常識,定位準(zhǔn)確信息就多,定位不準(zhǔn)信息就少,甚至是負的。且稱GPS信息是預(yù)言信息,而Shannon信息是統(tǒng)計信息。

把經(jīng)典信息公式（6）中的條件”yj”改為“yj為真”,即用 xi∈Aj取代yj,那么公式（4）就變?yōu)?

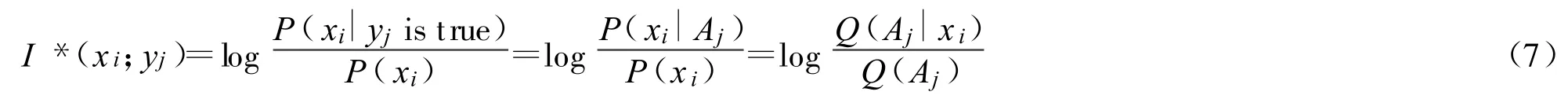
注意:除了需要先驗預(yù)測P（X）和真值函 Q（Aj|X）,還需要用以檢驗的事實X=xi。

由圖3可見,事實和預(yù)測完全一致時,即 xi=xj,信息量最大;隨著誤差增大,信息量漸漸變小;誤差大到一定程度信息就是負的。這是符合常理的。Q（Aj）越小,信息量越大。有兩個因素決定Q（Aj）大小,一是預(yù)測精度,即 σ,它越小,Q（Aj）就越小;二是 Q（Aj|xi）覆蓋區(qū)域的 P（xi）大小,P（xi）越小,Q（Aj）就越小。這樣就有結(jié)論:預(yù)測精度越高,或者事件越是出乎意外,信息的絕對值就越大。同時犯錯誤的可能性也越大,檢驗也就越嚴峻。如果經(jīng)得起檢驗,即Q（Aj|xi）較大,信息量就越大。這一公式非常符合Popper關(guān)于科學(xué)理論進步的信息準(zhǔn)則[12]。

1.3 理想GPS和普遍必然命題的信息

假設(shè)有理想GPS,被定義為:

（1）混淆概率僅取0,1二值;

（2）聲稱實際目標(biāo)100%落在指定范圍內(nèi)。

一個可能的混淆概率函數(shù)如圖2中的矩形所示。信息量公式變成

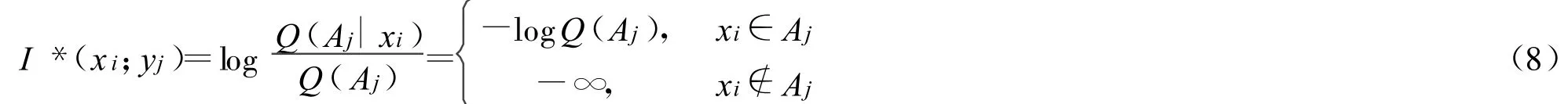
其圖解如圖3所示。

不難證明,只要有一個xi不在Aj中,求得的平均信息都是-∞。信息負無窮大就意味著:按照語義為分布是P（X|Aj）的信源編碼時,只要有一個 xi不在Aj中,則編碼長度無論多大,都會失敗。

根據(jù)Popper理論,對于普遍必然命題,只要有一個反例,該命題就被證偽了[12]。上面公式正好反映Popper的這一思想。根據(jù)公式,對于永真命題和永假命題,或者永遠半真半假的命題,都有 Q（Aj|xi）/Q（Aj）=1,所以信息量都是0。這和Popper理論一致。

日常語言中,由于接收信息者總是假定有意外事件的可能,或者說按模糊方式理解所有命題,負無窮大信息極少發(fā)生。

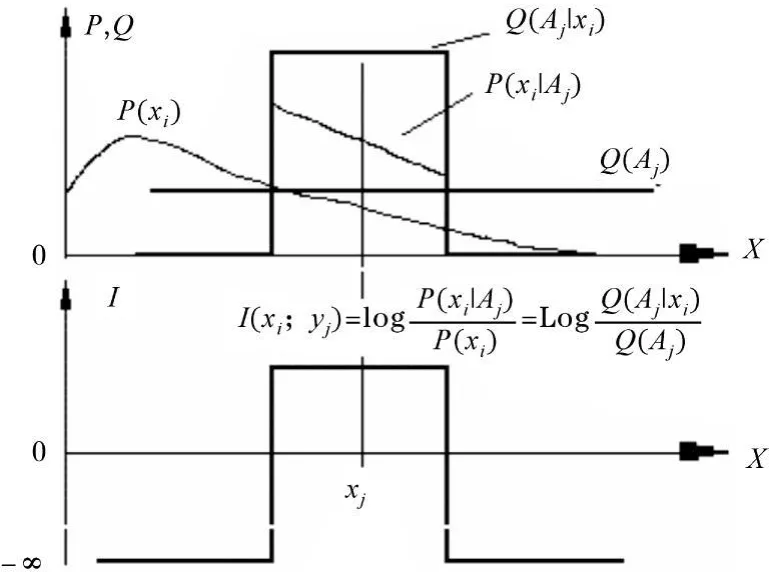
圖3 理想GPS和普遍必然命題提供的信息

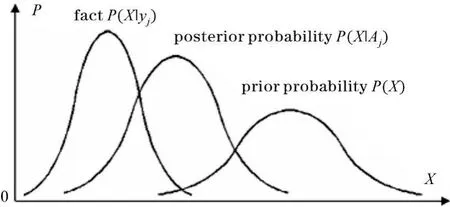
圖4 圖解廣義Kullback公式

1.4 廣義Kullback公式及其用于預(yù)測優(yōu)化

如何求yj提供關(guān)于X的平均信息,開始采用Kullback公式:

這里假設(shè)P（X|Y）=P（X|Y是真的）,即對于所有 xi,P（xi|yj）=P（xi|Aj）。但是實際上,兩者未必相同。后來發(fā)現(xiàn),保留對數(shù)左邊的條件概率,采用公式

反而使公式更有解釋力。這是非常重要的一步,因為這樣就能反映信息來自事實檢驗。這就是廣義Kullback公式。這里,P（xi|yj）就是證據(jù),而P（xi|Aj）是理論預(yù)測,P（xi）是先驗知識。Theil曾經(jīng)提出的信息差公式與此類似[13],但是上面公式含義更豐富。

可以把-logP（xi）理解為原先為P（X）按最優(yōu)式編碼時 xi的碼長,-log P（xi|Aj）理解為yj出現(xiàn)后為P（xi|Aj）按最優(yōu)方式編碼時 xi的碼長。這樣,I（X;yj）就是因預(yù)測yj而節(jié)省的平均碼長。

圖4表明,理論預(yù)測P（X|Aj）越接近事實P（X|yj）,信息量越大,最大值就是Kullback信息;信源或先驗估計P（X）越與事實P（X|yj）不同（表示預(yù)測的事情越是出乎意外）,信息量越大。

現(xiàn)在假設(shè)X是經(jīng)濟指標(biāo),用兩個參數(shù) xj和σj預(yù)測經(jīng)濟指標(biāo),即邏輯條件概率是

上面廣義Kullback公式就可以用于預(yù)測的評價和優(yōu)化。

設(shè)z是某種客觀因素,＜yj,σj＞表示一種預(yù)測,被預(yù)測的經(jīng)濟指標(biāo)的條件概率是P（X|z）。選擇哪個預(yù)測＜yj,σj＞最好 ,改變 ＜yj,σj＞,使廣義 Kullback 信息

達最大的＜yj,σj＞就最好。對于GPS精度 σ和讀數(shù)yj的選擇,上面公式同樣適用。

如果預(yù)測經(jīng)常不準(zhǔn),或者發(fā)信人有意說謊,收信人可以總結(jié)經(jīng)驗,修改語義,比如令

這樣將能使實際收到的信息接近統(tǒng)計信息。

1.5 廣義互信息公式

對I（X;yj）求平均,得到廣義互信息公式:

當(dāng)預(yù)測和事實一致時,I*（X;Y）可以寫成

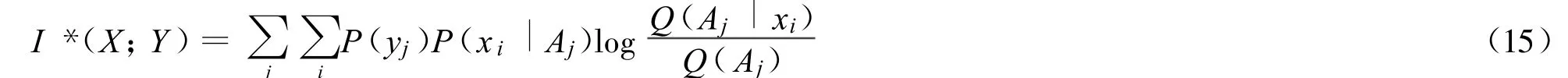
從上面公式可見,Shannon廣義互信息是廣義互信息在預(yù)測總是和事實一致時的特例。它也反映節(jié)省的平均碼長。Shannon互信息可以理解為通信成本,而廣義互信息可以理解為通信的效用,其上限是Shannon互信息。

2 限誤差信息率及其和信息率失真及復(fù)雜性失真之間的等價關(guān)系

2.1 從信息率失真到復(fù)雜性失真

在為聲音、視頻、經(jīng)濟、地理位置…數(shù)據(jù)編碼時,適當(dāng)?shù)挠惺д婢幋a將大大提高通信效率。為此Shannon提出Rate distortion理論[2],并且得到T.Berger等[14-15]的大力發(fā)展。

假設(shè)為數(shù)字X編碼,設(shè)離散隨機變量X∈A={x1,x2,…}和Y∈B={y1,y2,…}分別表示源碼和目的碼,信源是前后無關(guān)的。假設(shè)yj和xi之間的失真是dij=d（xi,yj）,那么它的平均值就是

給定離散無記憶信源P（X）和E（dij）的上限D(zhuǎn),改變P（Y|X）,求Shannon互信息的最小值:

R（D）就是信息率失真函數(shù)。Shannon證明了,它反映為每個數(shù)字編碼的最短平均碼長（通過分組編碼實現(xiàn)）或最小信息速率（忽略兩者之間的微小差別）。

有些文獻[15]區(qū)分了率失真函數(shù)和信息率失真函數(shù),前者是可操作性定義,考慮分組編碼和解碼;后者是信息定義,只考慮由信源到信宿的編碼。兩者被證明是等價的。據(jù)此,文中只考慮信息率失真函數(shù),不考慮分組編碼——其結(jié)論應(yīng)該和考慮分組編碼和解碼時的結(jié)論同樣。

然而,數(shù)據(jù)壓縮實踐中,需要對每對（xi,yj）之間的誤差給出限制。Kolmogorov提出基于其復(fù)雜性理論的結(jié)構(gòu)函數(shù)[5],最近又有人提出復(fù)雜性失真[6]。復(fù)雜性理論把一個字符串的最短編碼長度叫做這個字符串的復(fù)雜性。有失真編碼時,如果

成立,則對于每個xi,集合B上存在一個以yi為中心的失真球Bi,用球中任何一個yj表示xi都可以。同時對于任何yj,A上存在一個以xj為中心失真球Aj,yj可以是Aj中任何一個xi的代表。球的半徑都是D0.5c 。給定信源和失真球限制,可求出最小平均碼長或Shannon互信息（忽略微小誤差）,設(shè)為 C,它是Dc的函數(shù),即C=C（Dc）。它就是復(fù)雜性失真函數(shù)[6]。采用同樣的編碼,假設(shè)對于每個yj,失真球Aj中元素一樣多,為S=|Aj|,hx（Dc）=logS就是結(jié)構(gòu)函數(shù)。

也需要不同尺寸的容差集合或容差球,用以限制編碼誤差。比如,隨著顏色的明度增加,人眼對色差的敏感性減弱,這意味著,對于較暗的顏色,需要較小的容差,對于較亮的顏色,需要較大的容差。

2.2 定義限誤差信息率并證明復(fù)雜性失真是其特例

設(shè)AXB上存在相似關(guān)系,xi和yj之間的相似度是cij=c（xi,yj）=c（xi,xj）∈[0,1],如式（2）所示。對于每個xi,B上存在一個容差集合Bi,yj在Bi上的隸屬度是cij。對于每個yj,A上存在一個容差集合Aj,xi在Aj上的隸屬度也是cij。這也就是說,這些容差集合可以是模糊的,并且有

如果對于每個Bi,

稱一組集合 T={B1,B2,…}是對 xi,x2,…的編碼的容差。如果 B1,B2,…是清晰集合,即cij∈{0,1},上面限制變成

現(xiàn)在,在允許選擇和 xi相似的yj代表xi時,給定 P（X）和 T,改變 P（Y|X）,求最小信息速率 R（T）,

就是限誤差信息率。很顯然,當(dāng)B1,B2,…是分別以y1,y2為中心的大小一樣的球或區(qū)域,R（T）就變成C（Dc）。所以C（Dc）是R（T）的特例。

假設(shè)B1,B2,…是清晰集合時,看R（T）和R（D）之間的等價關(guān)系。

現(xiàn)在考慮函數(shù)R（D）。把 xi和yj之間的失真定義為:

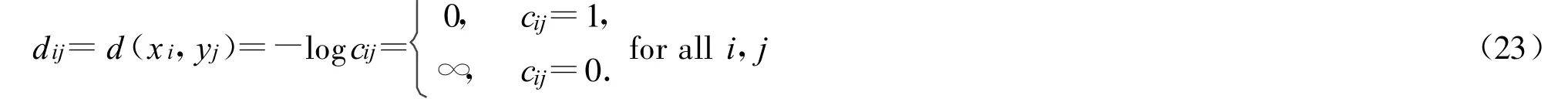
根據(jù)式（21）和式（23）,限制 E（dij）≤D=0和限制 T等價,即 R（D=0）=R（T）。所以 C（Dc）也是 R（D）的特例。

2.3 反映信息率失真和復(fù)雜性失真之間等價關(guān)系的廣義熵

下面證明,當(dāng) T是一組清晰集合時,R（D=0）等于一個廣義熵。

知道,Rate-distortion函數(shù)的參數(shù)表示[16]:

其中

令s=-1/（2σ2）,可以看出GPS信息和信息率失真之間的清晰聯(lián)系。這樣就可認為exp（sdij）=Q（Bi|yj）,λi=1/Q（Bi）,于是得到和（15）相似的公式:

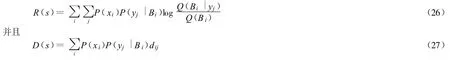
當(dāng)T是一組清晰集合時,exp（-∞）=0,exp（0）=1,D=0時,R和s無關(guān)。于是有

雖然Q（Bi）是P（Y）的函數(shù),但是并不是任何一個 H*（X）都等于一個R（D）。改變P（Y）使得 H*（X）達最小,設(shè)為 HP（Y）*（X）,它才等于 R（D=0）:

所以 R（T）=R（D=0）=HP（Y）*（X）。

僅當(dāng)所有Bi大小一樣呈球形時,才有C（Dc）=R（T）=R（D=0）。

給定 T時X的條件熵是

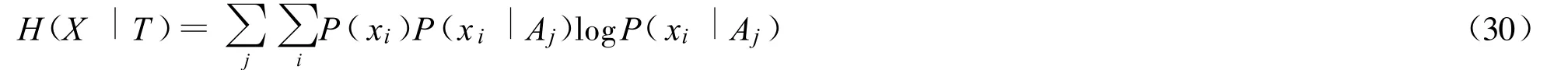
如果在每個失真球 Aj中元素相等,為S=|Aj|,并且等概率發(fā)生,H（X|T）就變成結(jié)構(gòu)函數(shù)hx（Dc）。

一般情況下,結(jié)論C（Dc）=R（Dc）[6]是不對的。肯定失真-信息率和期望的結(jié)構(gòu)函數(shù)之間有一般等價關(guān)系[5],也是不對的。因為在復(fù)雜性理論中,那些容差球是清晰集合,而在信息率失真理論中,那些容差球是模糊集合,后者較前者限制更松。下面用編碼例子說明它們的差別。

2.4 用一個編譯碼例子說明R（Dc）＜C（Dc）

這個例子也將顯示如何改變P（Y|X）從而減少I（X;Y）的思路。

Example:A={1,2,3,4},B=（1,2,3,4）,允許誤差|X-Y|≤1。給定P（X）,通過適當(dāng)?shù)木幋a得到R。

實際的數(shù)據(jù)壓縮過程是:P（X）→信源編碼→存儲和傳輸→解碼→P（Y）,這里不考慮中間環(huán)節(jié)（中間可能要采用分組碼）,只考慮用怎樣的編碼即P（Y|X）可以減少I（X;Y）得到 R。

由（28）式知,對于每個xi,邏輯概率Q（Bi）越大越好;不同的Bi之間相互越重疊越好。這樣條件熵H（X|Y）就較大,信息I（X;Y）=H（X）-H（X|Y）就較小。

如果簡單用y2表示 x1和 x2;用 y3表示x3和x4,平均信息量是1比特。參看式（25）和式（28）,采用優(yōu)化方法給信源編碼。讓X=1時,Y=2;X=4時,Y=3;X=2或3時,Y=2或3,隨機產(chǎn)生。這樣,就有表1數(shù)據(jù)。

表1 為C（Dc=1）尋找P（Y|X）

注意,Q（B2）=Q（B3）=1,所以X=2或3時,傳遞信息是0。有 R（T）=C（Dc）=-0.25log0.5-0.25log0.5=0.5比特。

但是,這時候E（dij）=0.75＜1。下面編碼可以證明R（Dc）＜C（Dc）。

現(xiàn)在令 dij=（yj-xi）2,求 E（dij）≤D=Dc=1時的R。令 s=-0.45,y2=y3=0.5,Q（Ai|yj）=exp[s（yj-xi）2],P（yj|xi）=P（yj|Ai）,于是有表2數(shù)據(jù)。

表2 為 R（D=1）尋找P（Y|X）

那么,根據(jù)式（24）,有 D=0.994,R（D）=sD+H*（X）=-0.447+0.816=0.369比特。

可見,一般情況下R（Dc）＜C（Dc）。

2.5 限誤差信息率和信息率失真之間的等價關(guān)系

假設(shè) T={B1,B2,…}是一組模糊集合,Shannon互信息是I（X;Y）=H（Y）-H（Y|X）。當(dāng)容差限制是 T或不等式（20）時,下式成立時:

P（Y|X）最分散,所以H（Y|X）最大。這個等式對于R是必要的,但不是充分的。改變P（Y）使 I（X;Y）達到最小值,就得到限誤差信息率函數(shù):

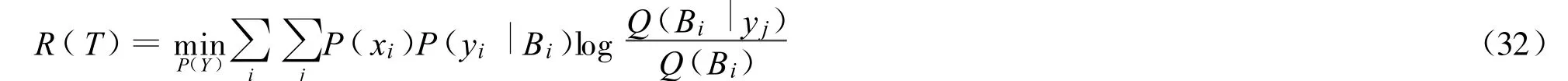
假設(shè) Q（Bi|yi）=exp（sdij）for all i,j,參看2.3節(jié),得到 R（T）==R（D）。這意味著 R（D）函數(shù)是 R（T）函數(shù)在 Q（Bi|yj）=exp（sdij）for all i,j時的特例。其中 s就反映預(yù)測的精度,s越大,所需要的信息速率就越大。

顯然,廣義信息測度和R（D）函數(shù)之間存在深刻聯(lián)系,它們都和誤差及語義密切相關(guān)。

3 結(jié)束語

以GPS為例,推廣經(jīng)典信息公式到廣義信息公式,討論限誤差信息率和信息率失真怎樣和廣義互信息公式相聯(lián)系,證明了信息率失真 R（D）是限誤差信息率R（T）的特例,而復(fù)雜性失真C（Dc）是信息率失真 R（D）的特例。

致謝:感謝汪培莊教授和吳偉陵教授的支持和鼓勵

[1] 魯晨光,廣義信息論[M].北京:中國科技大學(xué)出版社,1993.

[2] C E Shannon.A mathematical theory of communication[J].Bell System Technical Journal,1948,27:379-429,623-656.

[3] 魯晨光,廣義互熵和廣義互信息的編碼意義[J].通信學(xué)報,1994,15（6）:37-44.

[4] C Lu.A generalization of Shannon's information theory[J].Int.J.of General Systems,1999,28（6）:453-490.

[5] P D Grunwald,P B Vitany.Kolmogorov Complexity and Information Theory With an Interpretation in Terms of Questions and Answers[J].Journal of Logic,Language and Information,2003:497-529.

[6] D M Sow.Complexity Distortion Theory[J].IEEE T ransactions on Information Theory,2003,49（3）:604-609.

[7] P Z Wang.Random sets in Fuzzy Set theory[A].System&Control Encyclopedia,edited by M.G.Singh,Pergamon Press,1987:3945-3947.

[8] J B Tenenbaum,T L Griffiths.Generalization,similarity,and Bayesian inference[J].Behavioral and Brain Science,2001,24（4）:629-640.

[9] L A Zadeh.Fuzzy sets[J].Infor.Contr.,1965,18:338-353.

[10] L A Zadeh.Probability measures of fuzzy events[J].Journal of mathematical Analyses andApplications.1968,23:421-427.

[11] S Kullback.Information and Statistics[M].New York:John Wiley&Sons Inc.,1959.

[12] K R Popper.Conjectures and Refutations:The Growth of Scientific Knowledge[M].New York:Harper&Row,Publishers,1968.

[13] H Theil.Economics and Information Theory[M].North-Holland,Amsterdam,1967.

[14] T Berger.Rate Distortion Theory:A Mathematical Basis for Data Compression,Englewood Cliffs[M].NJ:Prentice-Hall,1971.

[15] T M Cover,J A Thomas.信息論基礎(chǔ)[M].北京:機械工業(yè)出版社,2008.

[16] 周炯盤.信息理論基礎(chǔ)[M].北京:人民郵電出版社,1983.