增城市GPS高程擬合精度研究

史經

(增城市金站城市建設測量隊，廣東增城 511300)

1 引言

高程擬合是在GPS點布設的區域內，根據已知點的平面坐標和高程異常ξ值，通過數值擬合的方法，擬合似大地水準面，再用似大地水準面數學模型內插求待定點的ξ值，進而求出待定點的正常高Hr［1］。

常用的擬合計算方法有:多項式曲面擬合、加權均值法、多面函數曲面擬合、線性移動擬合法、多層神經網絡法等?？紤]到模型的實用性及計算實現的方便性，本文選用了多項式曲面擬合法計算。

增城市 1 600 km2范圍內有2/3以上是山地，高程異常變化較大，通過最小二乘估計，使用二次曲面擬合的方法求得的正常高并不能精確反映真實的地形情況;如使用分區擬合，雖然能較好反映地形情況，但在數據處理時非常繁瑣，同時還涉及各個曲面的光滑連接處理，不太適用于實際生產［2］，因此，本文采用三次多項式曲面擬合法求得的似大地水準面模型來逼近大地水準面。

2 多項式函數擬合法的數學模型

多項式函數擬合法的基本思想是在GPS區域網內，將似大地水準面看成一個數學曲面，高程異常ξ表示為平面坐標(x，y)的函數，用聯測水準測量的GPS觀測點作為網中起算點，用已知高程異常值結合起算點的平面坐標值來計算測區內似大地水準面的模型，進而用在模型上內插就可求出其余各點的高程異常值［3］，其數學模型為:

式(1)中，Z(x，y)是擬合的似大地水準面;ε是擬合殘差。而:

式(2)中，a為擬合待定參數，x，y為各GPS點的平面坐標，p，q為多項式的階數。由最小二乘法得:

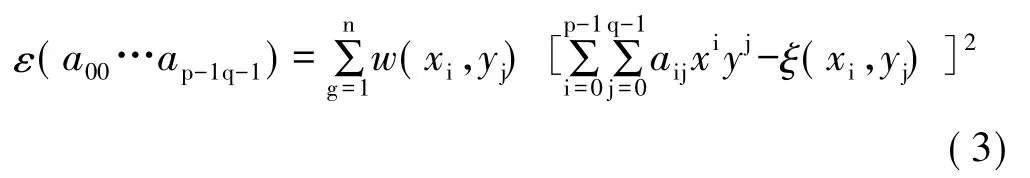
式(3) 中，點(a00…ap－1q－1) 是多元函數 ε(a00…ap－1q－1)的極小點，w(x，y)為權函數，從而 a00…ap－1q－1必須滿足方程組:

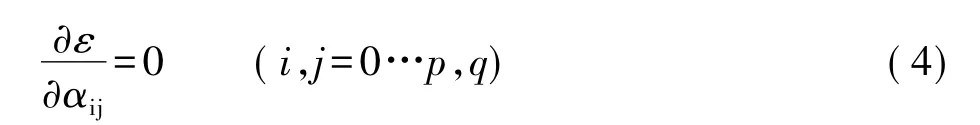
對ε函數求偏導，移項之后得:

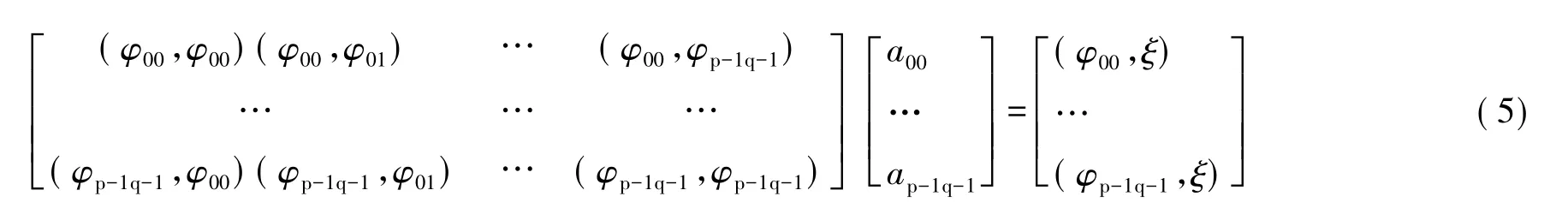
其中φij=xiyj。上式(5)可簡寫成 A×Aa=B，則可求出擬合待定參數為Aa=A－1×B。

再由式(1)、(2)可得出任意平面點對應的高程異常值ξ，再由公式Hr=HG－ξ推出正常高Hr。

3 擬合函數的評估

對于多項式擬合函數的評估采用一元回歸模型方法，所謂回歸模型方法，就是從一組地理要素(現象)的數據出發，確定這些要素數據之間的定量表述形式，即建立回歸模型。通過回歸模型，根據一個或幾個地理要素數據來預測另一個要素的值。模擬回歸模型時，必要條件是具有兩個相應變量系列，其中同一系列的每個元素完全相應于另一序列的元素，這時就可以實現內插和外推兩個任務［4］。

設觀測數據L=(ξ1ξ2…ξn)T，等權。選取擬合函數BX，相應的模型誤差為δ，L的觀測誤差為△，則其函數模型為:

用BX對L進行擬合，要求(BX－L)T(BX－L)=min(最小)，可得該方程為:

將式(6)代入，得:

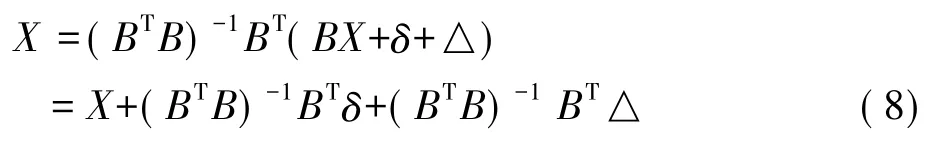
其中，BX+δ為理論模型，采用的實際模型為BX，其擬合誤差為:

回歸模型的精度，可通過ε來確定，根據最小二乘法原理，ε的平方和為最小是最好的，一般是采用回歸方程的剩余標準差來估計，即:

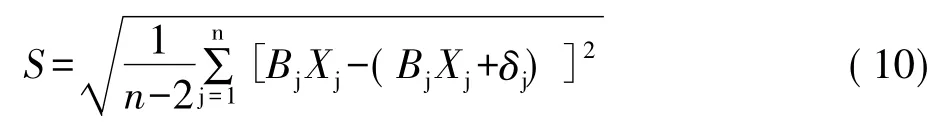
式(10)中，S的大小反映回歸模型的效果。通過回歸效果的顯著性檢驗，可以證明它是一個具有自由度(1，m－2)的 F 變量，即:

式(11)中:r為相關系數。可見，一元回歸時，回歸效果的好壞可以通過相關系數的大小來鑒別，因此，擬合函數的選取應該是:

(1)精度σ2給定時，擬合函數中引入的參數要盡可能地少，即要引入在觀測數據中占主要成分的那些主參數，次要參數盡可能地排除在擬合函數之外。

(2)最后確定的擬合函數，其參數必須按最優的準則確定，即采用最小二乘估計。

4 GPS高程擬合精度分析

4.1 項目概況

增城市1∶2000數字航測已覆蓋全市1 600多平方千米，2/3以上地形為丘陵和山區，北部山區高程異常值偏差較為明顯，擬合區域呈面狀分布。本次測量共采用四等以上水準聯測點105個，且均勻分布在全市各鎮，其中擬合點為102個(另外3個作為較差檢校點)，GPS水準聯測點分布情況如下圖1所示。

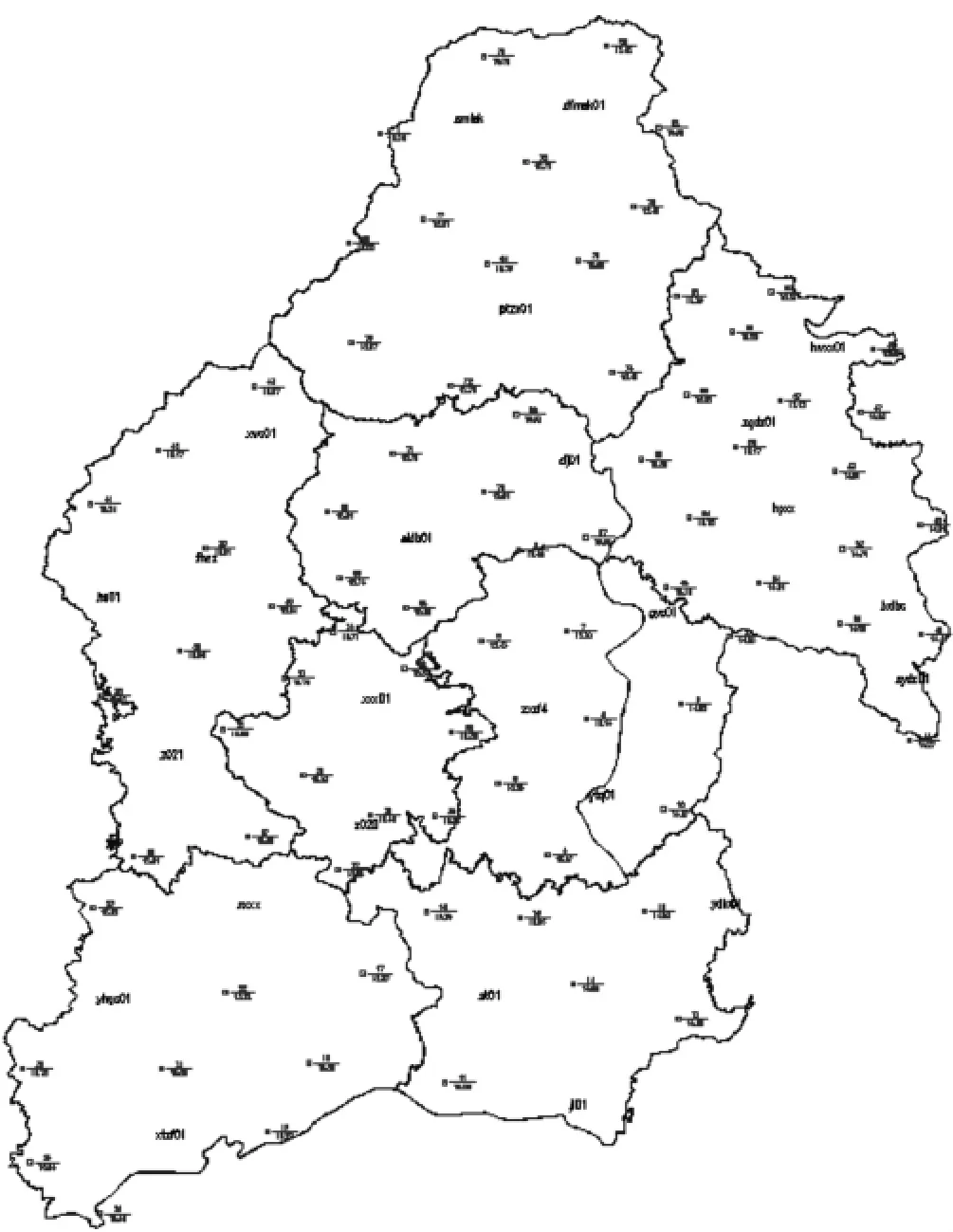
圖1 GPS水準聯測點分布圖

4.2 精度統計

通過擬合函數評估方法來選取擬合函數的模型，當擬合模型的估值精度σ2給定到一定值時，這時兩種函數的模型誤差δ會趨于接近;當再提高精度值σ2時，則其中一種模型誤差值會明顯增大。以下用102個已知正常高和大地高的擬合點(不計原始數據測量誤差)對不同次數的兩種多項式擬合模型分別建模后求殘差值，如表1所示。

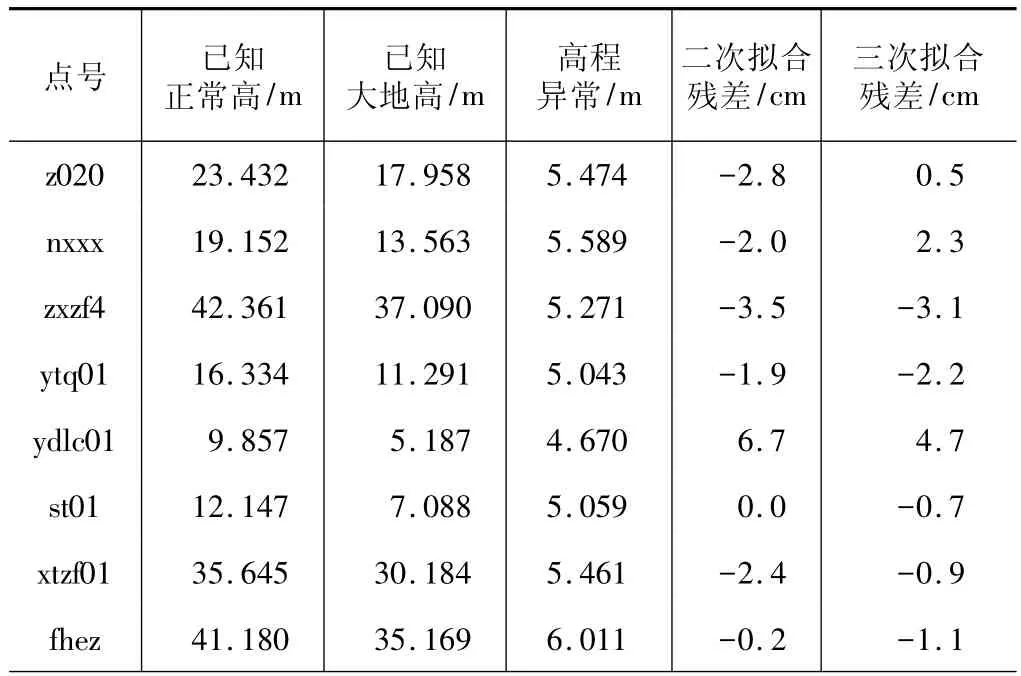
多項式擬合殘差統計表 表1

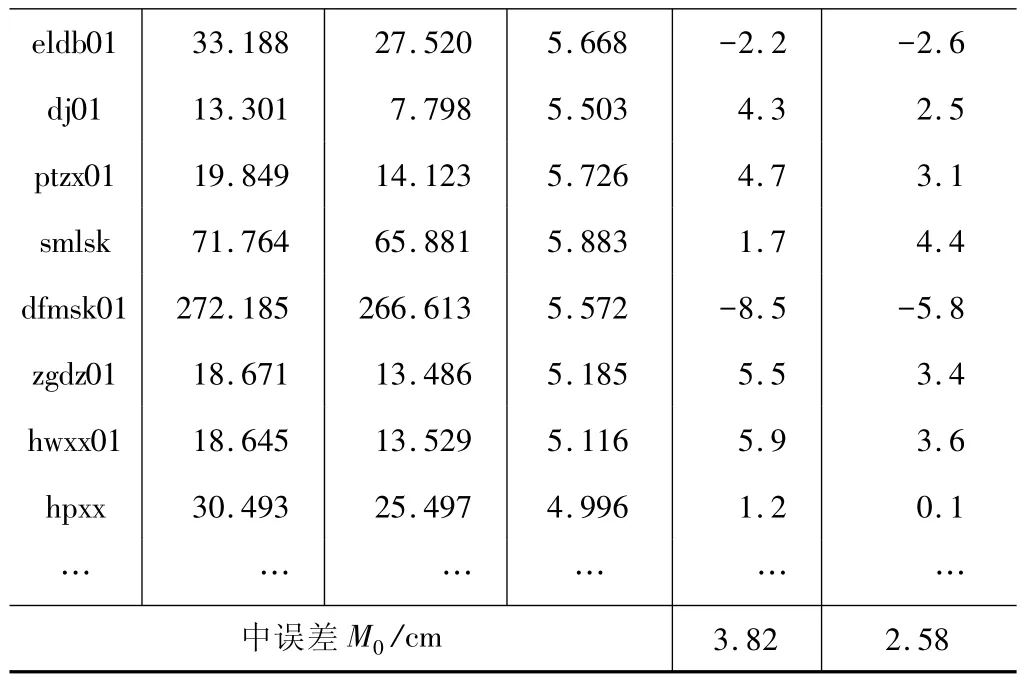
eldb01 33.188 27.520 5.668 －2.2 －2.6 dj01 13.301 7.798 5.503 4.3 2.5 ptzx01 19.849 14.123 5.726 4.7 3.1 smlsk 71.764 65.881 5.883 1.7 4.4 dfmsk01 272.185 266.613 5.572 －8.5 －5.8 zgdz01 18.671 13.486 5.185 5.5 3.4 hwxx01 18.645 13.529 5.116 5.9 3.6 hpxx 30.493 25.497 4.996 1.2 0.1……… … … …中誤差 M0/cm 3.82 2.58

求得二、三次多項式系數 a1、a2后，再由式(1)、(2)反推其他任意待定點的高程異常及正常高值。本次精度分析計算采用3個較差檢校點，較差數據如表2所示。

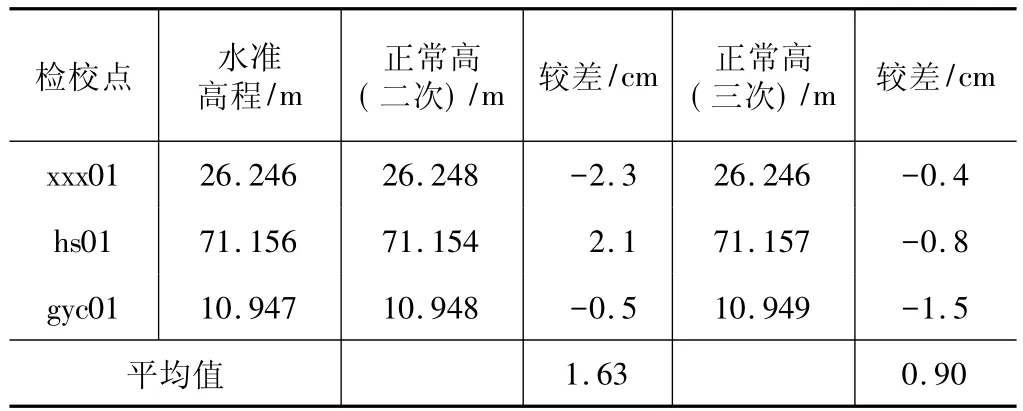
多項式模型精度比較表 表2

由表1和表2的統計數據獲得兩種擬合模型求得的正常高與水準高程值比較，三次多項式擬合殘差中誤差較小，僅為M==±2.58 cm，最大值為△Hmax=6.8 cm，最小值為△Hmin=0.1 cm，與水準檢校點比較，其較差平均值為0.9 cm，因此，三次多項式擬合在地勢起伏較大的地區具有精度高，誤差分布均勻的優點。

5 結語

(1)增城市地勢起伏明顯，南北高差可達 1 km以上，實驗結果證明用三次曲面擬合模型計算的似大地水準面比二次模型精度更高。多項式的次數應根據測區的實際情況來定，并不是越高越好，次數太高會出多個尖點，引起似大地水準面的不光滑，而且次數太高也會影響計算速度。

(2)似大地水準面是純幾何面，通常是光滑且起伏變化平緩的，因此，只要布點均勻合理，點數相當，用幾何模擬方法來確定其模型是可行的［5］。

(3)在高程異常起伏較小的平坦地區，可以用GPS高程擬合的方法代替普通幾何水準測量。對于面狀測區，參與計算的幾何水準點應盡可能包圍所有的擬合點;在地形復雜的測區，應適當增加水準重合點觀測。

［1］蔣詩洋.實時獲取GPS高程擬合關系研究［J］.測繪通報，2007(4):49 ～50，55

［2］姚興雙，于久申，滿雪峰等.局域CQG2000似大地水準面模型的數字化及應用［J］.測繪通報，2007(11):4～9

［3］于小平，楊國東，許惠平等.GPS RTK高程擬合方法精度研究［J］.測繪通報，2006(11):19～21

［4］李曉桓.GPS水準擬合模型的優選［J］.測繪通報，2003(7):11～14

［5］鄧興升.確定高程異常的統計學習方法［J］.測繪通報，2008(4):4～7