小波變換在電能質量擾動檢測中的探討

魏 茹，欒鵬飛

（鄂爾多斯電業局，內蒙古 鄂爾多斯017000）

0 引 言

現代社會中，電能已成為一種廣泛使用的能源，其應用程度成為一個國家發展水平的主要標志之一。電能是一種經濟、實用、清潔且容易控制和轉換的能源形態，又是電力部門向用電用戶提供由發、供、用共同保證質量的一種特殊產品。隨著國民經濟和科學技術的發展，對電能的需求量日益增加，同時對電能質量的要求也越來越高［1，2］。

由于暫態電能質量信號是非平穩信號，這正適用于小波變換的方法。將小波變換用于暫態電能質量分析領域，將具有FFT、STFT所無法比擬的優點。目前小波分析方法在很多領域得到了廣泛應用，尤其是小波變換在暫態電能質量分析領域中的成功應用。利用小波變換在信號突變點的特性，可以實現電能質量擾動信號起止時刻的檢測。

1 小波變換方法

小波就是最短最簡單的振動，它是由Morlet于1980年在進行地震數據分析工作時創造的。小波分析方法是一種窗口大小（即窗口面積）固定但其形狀可改變的時域局部化分析方法，它在高頻部分具有較高的時間分辨率和較低的頻率分辨率，而在低頻部分具有較高的頻率分辨率和較低的時間分辨率，所以被譽為“數學顯微鏡”。正是這種特性，小波變換具有對信號的自適應性［3，4］。小波變換由于具有時域局部化的特點，克服了以往FFT和STFT的缺點，特別適合于非平穩信號和突變信號的分析。

根據小波變換在信號突變點的特點，在小波變換局部模極大值理論的基礎上，通過二進小波變換對電能質量擾動信號進行分析，可以在時域實現比較準確的檢測。

2 小波變換的奇異性檢測理論［5，6］

信號突變點檢測是小波變換應用的一個很重要的方面。信號突變點在小波變換域常對應于小波變換系數模的極值點或過零點，并且信號奇異性的大小同小波變換系數的極值隨尺度的變化規律相互對應。因此，將小波變換應用于對信號的瞬態特征描述是極其有意義的。目前，小波變換已在該領域獲得了廣泛的應用。

說明：本文中的小波變換的定義不是傳統所用的內積形式：

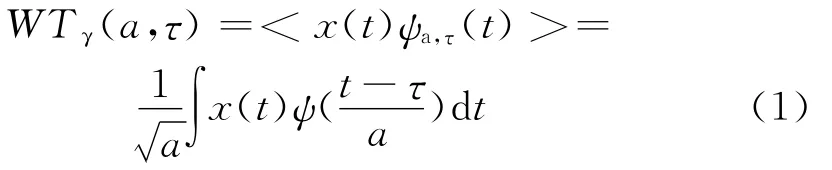
而是卷積形式：

這也就是把小波變換WTax（t）看成是信號x（t）通過激勵響應為ψa（1）（t）的系統后的輸出。兩種定義方式當ψ（t）和ψ（1）（t）都是實函數時，如果ψ（1）（t）＝ψ（－t），則有

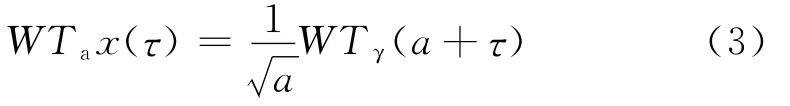
如非對稱，在計算方法上也沒有本質區別。

一般取尺度因子a＝2J，J∈Z，而t取連續變化的值，簡稱J為尺度。則上述小波變換被稱為卷積型二進小波變換。二進小波變換是穩定的、完備的，而且具有平移不變性，因此二進小波變換經常用于信號的奇異性檢測當中。

多尺度邊緣檢測則是采用平滑函數對信號的不同尺度下進行平滑，然后從一階導數或二階導數檢測其奇異點。多尺度邊緣檢測和小波變換檢測從思想方法上是一致的，以下直接從小波變換出發討論信號奇異性的多尺度檢測。

若θ（t）是某一起平滑作用的低通平滑函數，且滿足以下條件：

為方便起見，不妨取θ（t）為高斯函數，即

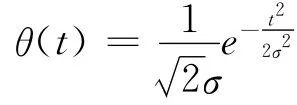
假定平滑函數θ（t）二次可導，并定義ψ（1）（t）、ψ（2）（t）分別是θ（t）一階、二階導數：

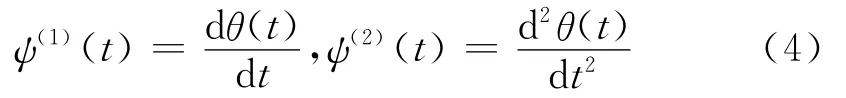
則函數ψ（1）（t）、ψ（2）（t）滿足小波的可容許性條件：

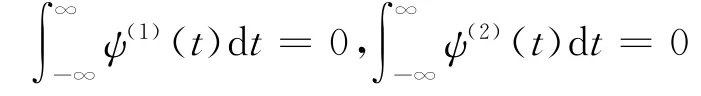
因此ψ（1）（t）、ψ（2）（t）可作為小波母函數。

若對任意函數g（t），引進記號

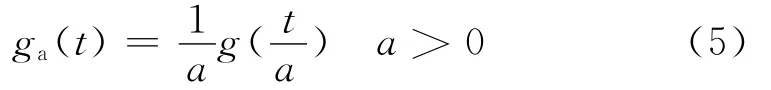
則ga（t）表示函數g（t）在尺度因子a的伸縮，由于小波變換就是通過將原信號f（t）同伸縮小波卷積得到的，以ψ（1）（t）為小波函數，函數f（t）在尺度因子a位置為t處的卷積型小波變換定義為：

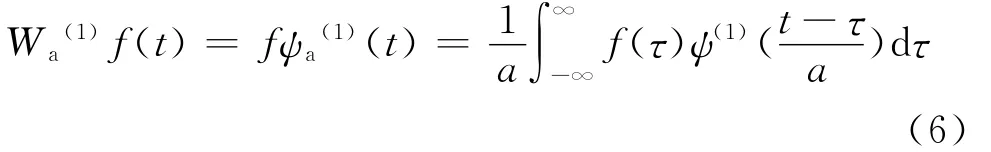
對應于ψ（2）（t）的小波變換為：

據此可以導出

由于fθa（t）可以看成是由低通平滑函數θ（t）在尺度因子a下對函數f（t）進行平滑的結果，由式（8）、（9）得知，小波 變換f（t）和f（t）可 分 別 理解為函數f（t）在尺度因子a下經平滑后的一階、二階導數。由上可知，當小波函數可看作某一平滑函數的一階導數時，信號的突變點（或邊緣點）與信號小波模的局部極值點相對應。當小波函數可看作是某一平滑函數的二階導數時，信號小波變換模的過零點，也對應于信號的突變點（或邊緣點）。

因此，采用檢測小波變換局部極值點和系數模的過零點的方法可檢測信號的突變點，這是兩種相似的方法。但是比較來說，用局部極值點進行檢測更具有優越性，由于函數fθa（t）的拐點既對應于它的一階導數模的極大值點，又對應于極小值點。極小值點（t1）對應于緩慢變化的點，而｜Wa（1）f（t）｜極大值點（t0，t2）是對應于信號尖銳變化的點，所以單憑檢測二階導數的過零點很難區分是信號的突變點還是緩慢點。因此，在信號奇異性檢測中，使用更多的是極大值檢測。

綜上所述，利用平滑函數一點導數構造的小波，其小波變換信號的尖銳變化點與模極大值將相對應，檢測其模極大值也就相當于檢測出了信號的奇異點，其小波變換在各尺度系數下的極大值對應于信號的突變點位置。只有在適當尺度下各突變點引起的小波變換才能避免交疊干擾，因此，在處理時應該把多尺度結合起來綜合觀察。

3 多孔算法［6，7，8］

離散信號的二進小波變換可以通過多孔算法來實現，它適用于a＝2J二分樹結構。它的計算過程是把沖激響應h0，h1序列（h0，h1為 Mallat算法中的濾波器組）的各點間插入適當零值再做卷積而得，將離散信號作為c0，計算過程如下：

hJ為h的相鄰兩項之間插入2J－1個零值。這樣就可以將離散信號各個采樣點的小波變換全部計算出來。

4 結束語

電能質量擾動持續時間、起止時刻是描述擾動的重要屬性，對電能質量擾動進行有效地檢測，有助于電能質量綜合評估，對于電能質量的綜合治理和提高具有重要意義。本文基于小波變換局部模極大值理論，采用二進小波變換對電能質量擾動進行檢測，其在分解尺度上可以實現較為準確的檢測。

［1］ 林海雪.現代電能質量的基本問題［J］.電網技術，2001，25（10）：5－12.

［2］ 肖湘寧，徐永海.電能質量問題剖析［J］.電網技術，2001，25（3）：66－69.

［3］ 胡 銘，陳 珩.電能質量極其分析方法綜述［J］.電網技術，2000，24（2）：36－38.

［4］ 張 斌，劉曉川，許之晗.基于變換的電能質量分析方法，電網技術［J］.2001，25（1）：26－29.

［5］ 彭玉華.小波變換與工程應用［M］.北京：科學出版社，1999.

［6］ 楊福生.小波變換的工程分析與應用［M］.北京：科學出版社，1999.

［7］ Mack J Shensa.The Discrete Wavelet Transfor m：Wedding the A Trous and Mallat Algorithms［J］.IEEE Transactions on Signal Processing，1992，40（10）：2464－2482.

［8］ Olivier Rioul，Pierre Duhamel.Fast Algorith ms for Discrete and continuous Wavelet transf or ms［J］.IEEE Transactions on Inf or mation Theory ，1992，38（2）：569－586.