高校食堂標準化管理體系創(chuàng)新思路分析
李賽杰,張晨光
(1.湖南大學,湖南長沙 410000;2.河南工業(yè)大學,河南鄭州 450000)
高校食堂的食品安全、菜品質量及員工誠信度關乎高校的和諧穩(wěn)定和師生的生命健康及身心發(fā)展,是一項重要的民生問題。高校食堂具有服務對象廣、人員聚集性高、風險點密集、社會關注度高等特點,因此高校亟需提升食堂管理水平和構建高校食堂標準化管理體系。目前高校食堂標準化管理主要是運用標準運營框架固定生產環(huán)節(jié)中反復存在的事物,使高校食堂以制度化、流程化、科學化的管理標準運行和發(fā)展[1],雖然現(xiàn)存食堂管理模式及經驗方式在整體上更新與時俱進[2-3],但是仍存在管理模式滯后、經驗陳舊等管理短板,具體表現(xiàn)為師生反映食堂飯菜品種單一、營養(yǎng)不均衡、價格昂貴、份量不足或過多等管理不到位現(xiàn)象。因此,本文從后廚日常管理、安全管理、營養(yǎng)管理等角度出發(fā),提出高校食堂標準化管理體系新思路,旨在為高校食堂工作的順利開展及管理水平、服務質量的有效提升等提供理論依據。
1 探索后廚標準化管理體系新模式
1.1 集約化采購管理模式
高校食堂餐飲服務立足于高校,具有公益性定位,要能保障高校食堂餐飲的食品安全與衛(wèi)生,注重師生的膳食與飲食營養(yǎng)結構。原材料采購是高校食堂日常工作的第一關,建立可追溯來源的食品質量安全保障機制并嚴格把控原材料物資的采購是確保食堂伙食的質量安全和降低食堂飯菜價格的重要抓手。目前高校食堂大多采取公開招標和零星采購等單一方式[4],不能對原材料價格、質量、貨源進行及時有效的管理,而高校食堂原材料可綜合考慮通過政府采購平臺、高校統(tǒng)一的互聯(lián)網采購、農校對接、公開招標和零星采購等混合模式進行科學合理采購,再由專業(yè)的食品檢測員對所采購的物資進行農獸藥殘留及微生物等指標的檢測,然后對檢測合格的原材料采用搬運系統(tǒng)分析方法進行合理儲藏使用,這樣可由政府部門或高校共同規(guī)范化管理,進而減少農產品生產、收獲、儲運、加工過程中的不科學行為的發(fā)生,避免農產品安全責任事故向校園蔓延,從源頭上保證了高校師生的健康與安全,從而為高校餐飲健康、可持續(xù)地經營發(fā)展奠定堅實基礎[5]。
1.2 科學化生產管理模式
高校食堂生產過程可采用PDCA循環(huán)法進行管理,PDCA循環(huán)一般要經過4個環(huán)節(jié)(計劃Plan、執(zhí)行Do、檢查Check、處理Action)和8個步驟(找出問題、找出問題原因、找出原因關鍵點、制定計劃、執(zhí)行、檢查、總結經驗、分析并提出新問題)[6]。目前高校食堂生產績效考核指標主要是針對食堂管理者制定的指標考核,缺乏系統(tǒng)的完整的基層員工關鍵考核績效體系,導致基層員工工作熱情度和創(chuàng)新度不高,績效管理不能發(fā)揮正常激勵作用[7]。結合高校食堂經營模式,可建立高校食堂管理者及基層員工的關鍵績效考核指標(Key Performance Indicators簡稱KPI),食堂管理者以營業(yè)額、利潤率、師生滿意率、管理創(chuàng)新性和員工優(yōu)秀率等作為關鍵指標,而食堂基層員工則以“周明星”、菜品創(chuàng)新性、師生滿意度、原材料節(jié)約性以及出勤率等作為關鍵績效考核指標,并在短期內實施獎懲制度,讓員工在最短時間內看到自己努力工作的成果,以此來提高員工積極性和工作效率。
1.3 合理化售賣管理模式
高校食堂售賣管理是前期采購及生產過程管理效果的直接體現(xiàn),也是員工績效考核的關鍵環(huán)節(jié)之一。隨著互聯(lián)網行業(yè)的快速發(fā)展,售賣模式向精細化和個性化轉變。在當前防疫形勢下,大多數(shù)高校食堂采用Online To Offline(簡稱O2O)線上售賣模式和食堂現(xiàn)場售賣模式相結合的售賣管理模式來提高師生就餐率及滿足師生多元化的就餐需求[8-9]。由于O2O線上售賣價格比較直觀,而售賣份量比較微觀難衡量,所以師生對于價格的敏感度也更高,為了滿足師生的偏好消費金額,需要對O2O線上售賣模式和食堂現(xiàn)場售賣模式采取合理的售價方法。結合高校食堂的經濟性及公益性定位,可采取黃金定價法則(又叫黃金分割定價法)應用于食堂創(chuàng)新菜品,非盈利性產品定價原則應用于食堂保障性低價菜品,可溢價性產品定價原則應用于食堂水吧、超市、糕點店等產品的售賣。
2 創(chuàng)建食堂食品安全管理體系新方法
我國2000—2020年食品安全研究者發(fā)表論文情況見圖1。由圖1可知,我國食品安全研究數(shù)量呈急速上升趨勢,在2016年左右研究數(shù)量漲幅收窄,而在2020年食品安全理論研究數(shù)量減少,更多學者偏向于食品安全創(chuàng)新管理實踐應用方向。
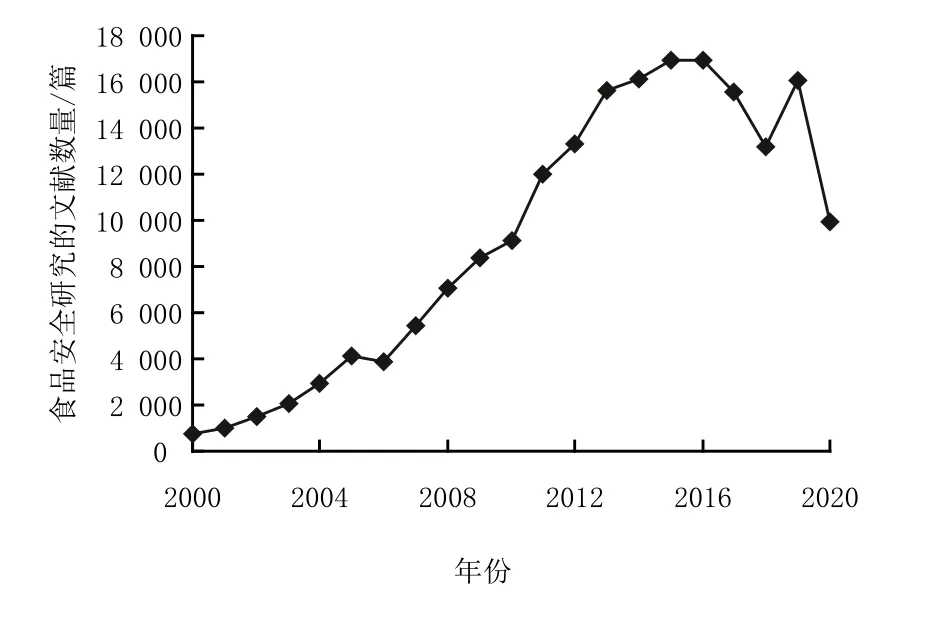
圖1 我國2000—2020年食品安全研究發(fā)文數(shù)量圖
2.1 基于KAP理論模式推進高校食堂食品安全管理工作
目前高校食品安全事件主要是食品安全管理人員與食品安全從業(yè)人員缺乏食品安全知識或食品安全管理不到位等原因造成的。知信行理論模式(Knowledge,Attitude,Practice,簡稱KAP)是員工將食品安全知識以積極的態(tài)度靈活運用到食堂安全管理體系中的模式。高校食堂引用KAP理論模式不僅可以充分調動員工工作的自主積極性和發(fā)揮知識的運用性,同時還可以增強員工的成就感和歸屬感,以此提高食堂安全管理效能,打破原有的只靠監(jiān)管的思維模式,實現(xiàn)食堂以人為本的創(chuàng)新管理服務模式[10]。
2.2 基于STP理論模式推進高校食堂食品安全管理工作
目前高校食堂經營模式主要有自管自營制、對外承包制和混合經營制。高校食堂是市場的一部分,運用營銷學的STP理論對高校食堂進行市場細分(Segmenting)、明確目標市場(Targeting)和市場定位(Positioning),以便能更好地針對高校大學生進行目標管理[11]。高校食堂STP戰(zhàn)略分析主要是依據不同地區(qū)、人口、心理及行為等因素對高校大學生的不同飲食文化差異進行劃分,然后明確高校食堂服務的目標市場,并將高校大學生按博士生、碩士生、本科生、專科生等層次學歷進行定位,通過集中化和差異化管理策略來塑造高校品牌食堂,進而為廣大師生提供優(yōu)質安全菜品和優(yōu)質服務質量。
2.3 基于HACCP模型的應用推進食堂食品安全管理工作
高校食堂是高校食品安全管理的重點區(qū)域,引用HACCP 體系(Hazard Analysis Critical Control Point)于高校食堂的初級生產至最終消費全過程,并通過對特定的危害及控制措施進行確定和評價,從而確保高校食堂的食品安全。HACCP體系主要包括7大原理,即危害分析、確定關鍵控制點、制定關鍵限值、建立關鍵控制點監(jiān)控體系、建立糾正措施、建立驗證程序、建立關于所有程序的文件并保持以上原理和應用的適當記錄。魏強等[12]認為HACCP體系適用于高校食堂的食品安全管理,通過對食堂菜品進行危害分析得出原材料、加工、清洗及人員4個關鍵點,然后制定并實施HACCP計劃,得出此方法可以有效控制菜品的食品安全風險。
2.4 基于SOP標準化操作程序的應用推進食堂食品安全管理工作
標準化食堂是目前各高校創(chuàng)建和改造食堂的標準,標準化食堂中必不可少的就是SOP(Standard Operation Procedure)標準化操作程序,其是食堂的工作指南和支柱,用于指導和規(guī)范日常工作,其精髓是將某一程序中的關鍵控制點進行細化和量化,然后在此基礎上達到標準化。李軍等[1]認為通過日常工作的反復實踐,形成一套標準化、細化、量化和優(yōu)化的操作流程,然后運用于食堂食品安全過程管理中,以此提升食堂的食品安全管理水平和服務質量,進而使高校食堂管理逐步走向科學化、規(guī)范化、常規(guī)化和程序化發(fā)展。
2.5 基于建立高校食堂安全評價模型推進食堂食品安全管理工作
目前高校食堂安全形勢依然嚴峻,影響高校食堂食品安全的因素頗多,各因素之間呈現(xiàn)出一種多維、非線性關系,因此系統(tǒng)性分析評價高校食堂食品安全情況較為困難。周文輝等[13]認為高校食堂可以基于4M理論(Men,Machine,Mecdium,Management)梳理影響高校食堂本質安全的因素,然后利用BP神經網絡法(Back Propagation)建立食堂食品安全評價模型,該模型從人、物、環(huán)境、管理等4個方面出發(fā),對各要素飲食安全進行分析,得出該模型在評價高校食堂安全管理水平上具有可行性和可靠性。
總之,高校食堂安全管理工作可以將上述5種方法有效結合,形成閉合環(huán)路,來探索分析食堂食品安全管理方法。首先簡單地將KAP理論模式作為員工補充知識培訓的關鍵環(huán)節(jié);其次使用STP理論模式對高校不同食堂進行劃分和定位,找出學生群體進行針對性管理;接下來運用HACCP模型對食堂飯菜生產過程進行危害分析,確定各環(huán)節(jié)的關鍵控制點;然后采用SOP標準化操作程序進行食堂標準作業(yè),并將其關鍵控制點進行細化和量化;最后通過建立安全評價模型對高校食堂的本質安全因素進行分析,最終評價高校食堂食品安全管理的可行性和可靠性。
3 引進食堂食品營養(yǎng)管理體系新技術
我國2000—2020年食品營養(yǎng)研究者發(fā)表論文情況見圖2,由圖2可看出我國食品營養(yǎng)研究數(shù)量整體呈緩慢上升趨勢,近4年食品營養(yǎng)研究數(shù)量略有波動,但2020年比2019年食品營養(yǎng)理論研究數(shù)量減少,更多學者偏向于食品營養(yǎng)創(chuàng)新管理實踐應用方向。
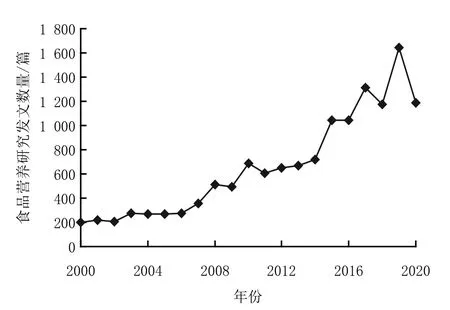
圖2 我國2000-2020年食品營養(yǎng)研究發(fā)文數(shù)量圖
為滿足高校食堂多元化的營養(yǎng)需求,應設置高校食堂專職營養(yǎng)師。《中國居民膳食指南》是高校食堂餐飲營養(yǎng)管理的基礎,其指導食堂菜品制作并使之能量適當、食物多樣、營養(yǎng)充足。專職營養(yǎng)師可以對高校內不同學歷層次的學生根據學業(yè)任務輕重情況進行配餐,對不同年齡段的教職工根據營養(yǎng)素的需求情況進行配餐,同時對素食主義者和輕食主義者等特殊群體進行配餐,然后貼上營養(yǎng)標簽,以供廣大師生參考選擇所需營養(yǎng)菜品[14]。另外,目前高校大力發(fā)展校園智慧餐飲建設,食堂智能設備的投入及自助餐形式的供給使得高校食堂菜品的營養(yǎng)搭配邁上新臺階,高校食堂運用營養(yǎng)標稱評價法分析高校食堂師生選擇菜品的營養(yǎng)標識,然后進行營養(yǎng)聲稱及評價,以期對廣大師生提供針對性的營養(yǎng)消費建議[15]。
4 結語
高校食堂標準化管理是新時代高校食堂發(fā)展的需要,也是落實國家立德樹人根本任務的重要舉措。高校食堂標準化管理體系涉及多方面內容,其創(chuàng)新過程也涉及多個層面。本文主要通過采用集約化采購管理模式、科學化生產管理模式及合理化售賣管理模式探索后廚標準化管理體系新模式;通過運用KAP理論模式、STP理論模式、HACCP模型、SOP標準化操作程序以及建立高校食堂安全評價模型等創(chuàng)建食堂食品安全管理體系新方法;另外通過采用營養(yǎng)標簽及營養(yǎng)標稱評價法來引進食堂食品營養(yǎng)管理體系新技術;然后再進行不斷探索、完善和更新高校食堂標準化管理體系,以此構建更加完善和多元化的高校食堂標準化管理體系,以提升廣大師生對食堂的滿意度,并為學校及自身的發(fā)展奠定堅實的基礎。

