隨機不平度激勵下公路路面交通荷載特性數值分析

陳德奇

（長沙理工大學交通運輸工程學院 湖南 長沙 410075）

文獻及測試試驗研究表明，行駛于路面的車輛對路面結構產生的交通荷載為隨機荷載，其分布規律與路面不平度密切相關，而與車輛本身結構的振動相關性不大[1]～[5]。故在不考慮交通荷載的縱向及橫向作用、只考慮垂向作用時，可認為隨機交通荷載僅是路面不平度的函數，即將路面不平度作為輸入項輸入給交通車輛產生隨機交通荷載，隨機交通荷載再作用于路面結構，引起路基路面結構層的動力響應，從而產生動力變形及位移。而路面不平度亦為隨機分布，無法用確定的表達式來描述它，只有通過實測和計算機處理方法產生。如果沒有實測的理想數據，通過計算機模擬一個路面不平整度隨機函數，使其功率譜密度與所要求的路面功率譜密度相一致，問題就可以獲得解決，依據所有路面結構類型的功率譜密度即可建立路面功率譜[6]～[8]。本文引入國際標準路面功率譜PSD（Power Spectral Density），并借助實測資料，采用數值方法，分析路面不平度作用下重載車輛交通隨機荷載的產生機理及其特性，從而為隨機交通荷載譜的建立提供依據。

1 數值模擬方法

1.1 數值模擬基本參數

為探究普遍意義上的車輛動荷載變化規律，故引入兩自由度的四分之一平面車輛模型進行求解，模型如圖1所示。圖中Ms為簧載質量，即車身部分質量，包括所有車身彈簧懸架的汽車部件，將其視為完全剛體來處理，如車架、車身、貨箱等，模型中忽略了人的影響；Mt為非簧載質量，即輪胎質量；Ks為懸架剛度；Kt為輪胎剛度；Cs為懸架阻尼；Ct為輪胎阻尼；Zs為簧載垂直位移；Zt為非簧載垂直位移，uy為路面不平度激勵[3][9]。所用的路面不平度激勵為標準路面譜密度函數（PSD），部分為不平度實測資料[6][8]。車輛模型參數采用某典型國產重型滿載時的車輛參數，如表1所示。

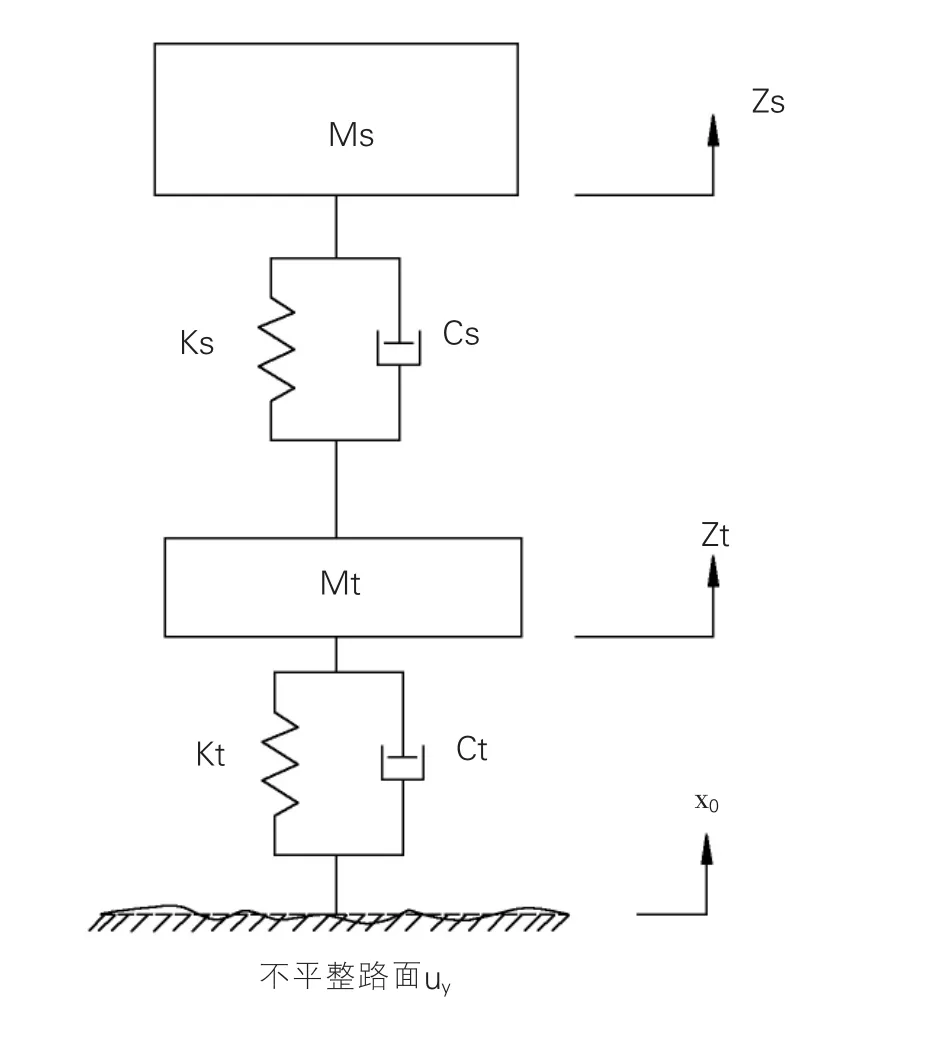
圖1 兩自由度四分之一車輛模型

表1 某國產重型汽車車輛模型參數（滿載）

為便于比較，取幾種標準路面譜密度[4][8]（分別屬于A、B、C三級路面）和車速狀態進行模擬，見表2。

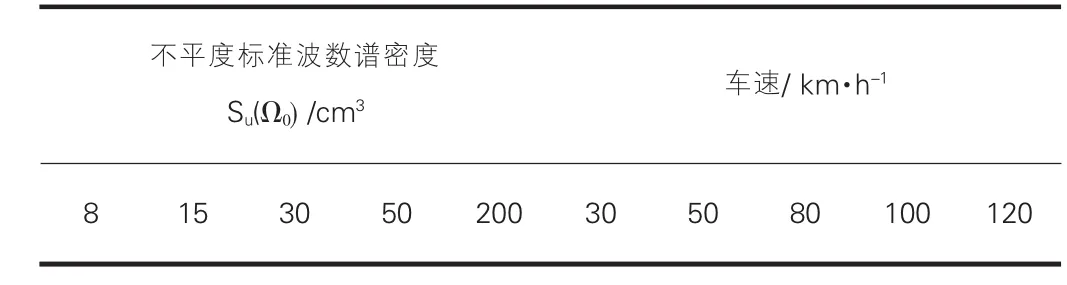
表2 路面參數及車輛狀態

1.2 數值模擬程序

由于MATLAB開發平臺具有強大的數值分析及數值計算能力，故本文借助于該平臺二次開發了隨機動載計算程序D-loads。該程序的編制參考了相關文獻[2][9]中一些近似程序。該程序適用于多自由度振動系統，根據不同車型建立的不同車輛模型均可通過輸入參數的大小和多寡的改變來實現模擬[10]。程序可通過改變車速的設置來考察車速對路面動載的影響，車速變化設置可模擬實際行車速度檔。路面激勵可直接輸入路面不平度檢測幅值數據，也可通過程序選擇系統輸入路面不平度譜密度參數來模擬動載時程。程序模擬過程見圖2。

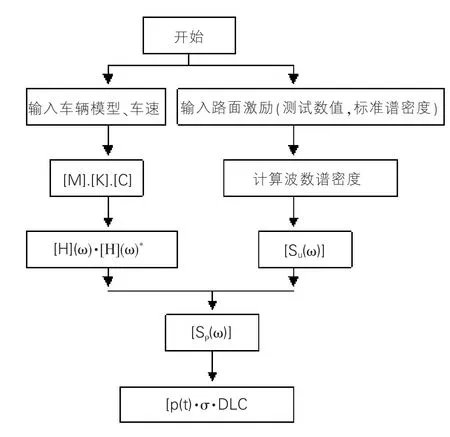
圖2 車輛隨機動載模擬程序框圖

2 數值模擬結果分析

2.1 動態荷載時程曲線

圖3為輸入一段已運營五年路面的不平度實測幅值數據后得到的動荷載時程曲線，圖4為新建公路荷載時程曲線。由圖中可看出，新建路面所激勵得到的動荷載明顯要比舊路小，新建路的最大動載超載率為17.1%，而舊路的最大動載超載率為35.7%，這進一步說明路面表面狀況與車輛動載之間關系密切。

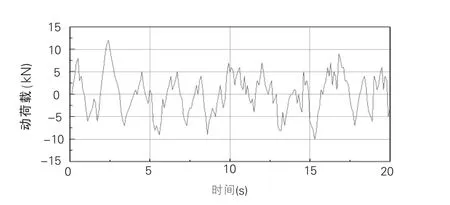
圖3 已運營路面動載時程曲線

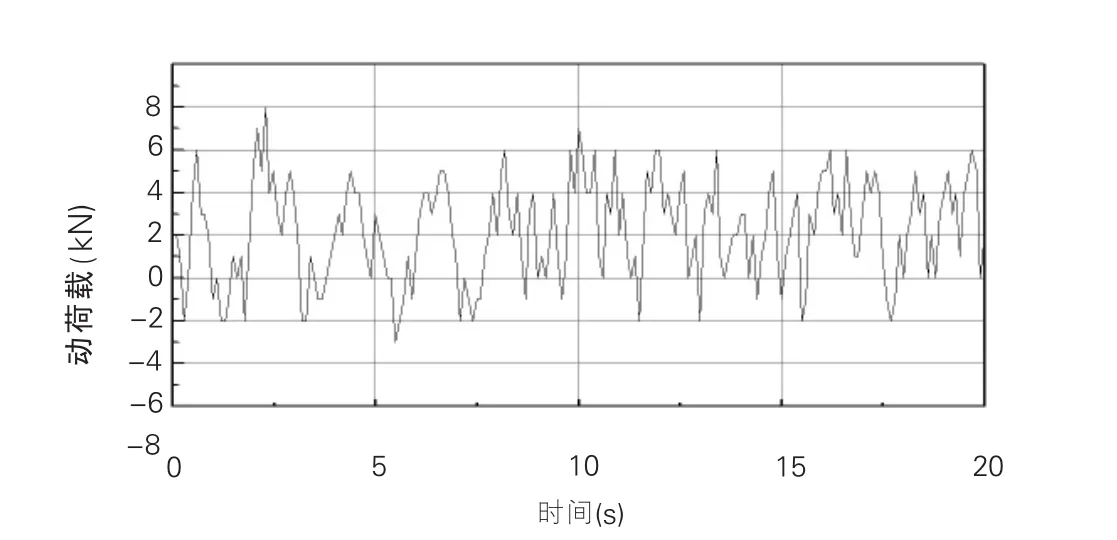
圖4 新建路面動載時程曲線

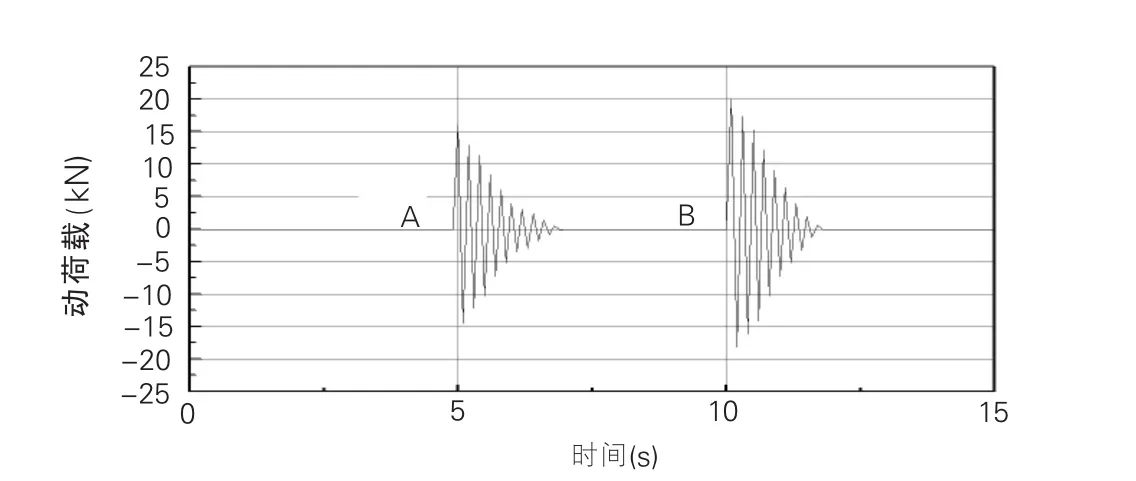
圖5 路面存在沉降高差時的動荷載

對于舊路，如果路基發生不均勻沉降形成反射裂縫使得路面發生斷裂形成沉降差 （路橋過渡段可視為相同情況），該沉降差（縱向上形成為小陡坎）造成車輛動載的突然加大也可通過程序反映出來。如果假設A點沉降差為1.0cm，B點沉降差為2.0cm，車輛到達A、B點之前路面假設為理想平面 （無高差），則圖5為這種情況模擬結果。由圖可知，車輛通過沉降差路段時產生的瞬時沖擊動荷載比較大，如沉降差為2.0cm時，瞬時超載率達到了63%，并且車輛存在一個顛簸過程，動荷載在正負之間急劇變化，沉降差越大，瞬時動荷載越大，說明只要路面一旦由于不均勻沉降出現裂縫，其后期破壞速率主要是由車輛動荷載控制。

2.2 激振頻率與動荷載的關系

圖6為利用程序獲得的路面不平度激勵與動荷載功率譜密度之間的關系，其中車速為100km/h，路面不平度譜密度Su(ΩO)=30cm3。由圖可知，當激勵處于低頻范圍時，動荷載功率譜密度達到最大值，說明路面不平度在低頻位置激振能量較高，而在高頻位置激勵能量比較低，即路面低頻段更容易產生較大交通荷載，從而首先成為損傷破壞區。

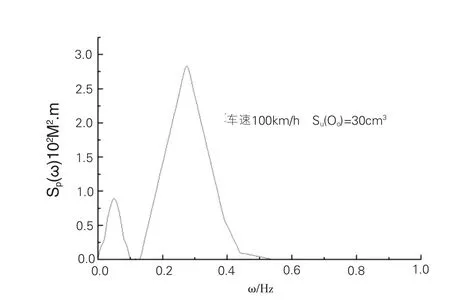
圖6 動載譜密度與激勵頻率關系

表3 車速與動荷載的關系

2.3 車速及路面波長與動荷載的關系

表3為根據一段新建高速公路路面譜計算后得到的不同車速下動荷載的最大值Pmax統計及按功率譜方法（開方）得到的動荷載的均方根值σp。由表可知，隨著車速增大，車輛動荷載呈增大趨勢，并且，動荷載峰值幾乎是均方根值的3倍，說明在研究路面結構的損傷破壞時動荷載的最大值變化范圍值得重視。

圖7為不同車速條件下的動荷載功率譜密度曲線，由圖可知，車速與動載功率譜密度成正比，車速的增加，相應動載功率譜增大。并且隨著車速的提高，路面激振頻率向頻率更低方向移動，說明車速提高時，路面長波路段對車輛的激振能量增強。

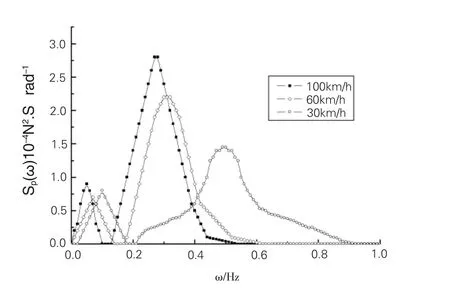
圖7 不同車速下動載功率譜圖

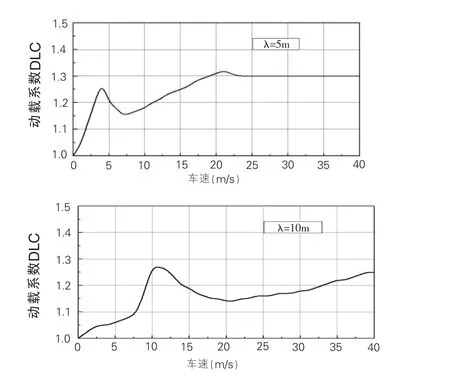
圖8 動載系數隨車速的變化

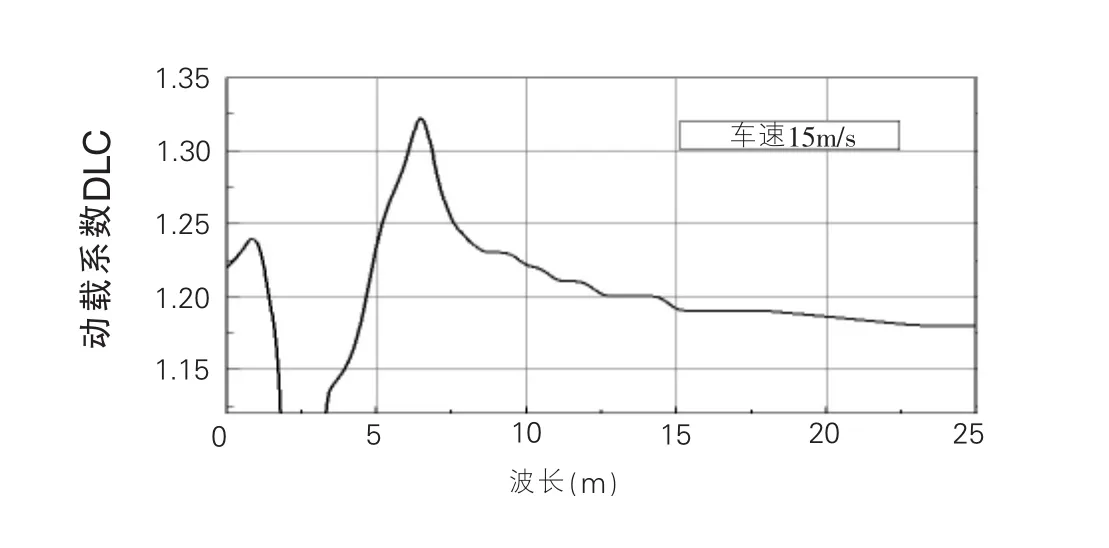
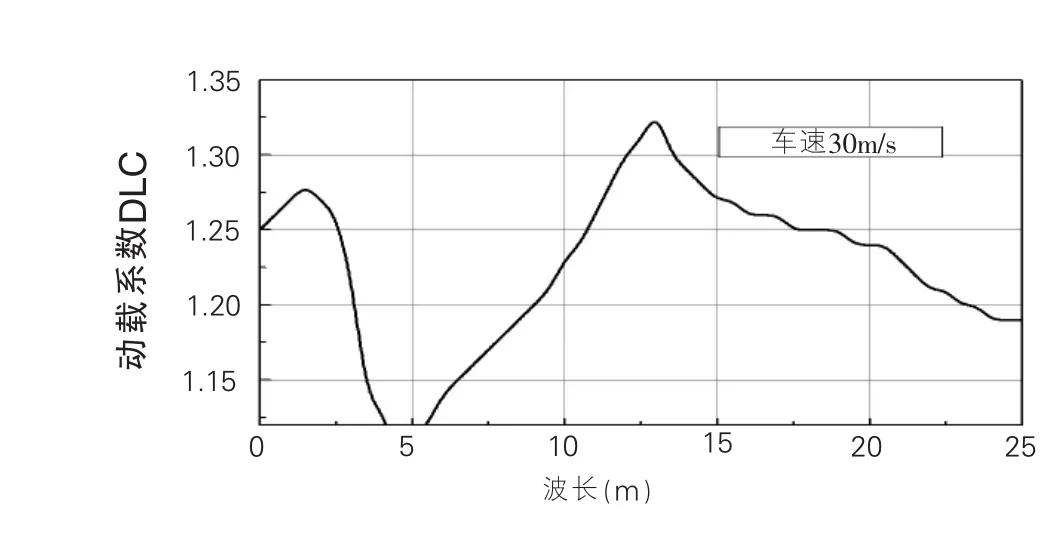
圖9 動載系數隨路面波長的變化

圖8為車速變化時，車輛動載系數的變化趨勢，圖9為波長變化時，車輛動載系數變化趨勢。由圖可知:（1）當車速為零時，動載系數也為零，這和實際情況是一致的，因為車輛靜止時，并不會產生附加動荷載。（2）當路面波長較小時（λ=5m），隨著車速的提高，動載系數會出現兩個峰值，峰值位置對應的頻率和車輛模型的固有頻率相近，說明此時車輛系統產生了共振。而隨著路面波長變長（λ=10m），動載系數出現峰值時的車速隨之提高，由于車速的限制，此時動載系數只出現一個峰值。說明動載并不隨車速呈線性增長，在某一車速時，車輛產生共振，動載將達最大值，而高于或低于該車速時，動載都將減小。可以預見，當波長進一步加長，動載系數的兩個峰值將都不會出現，動載系數將變的很小，此時，路面可近似認為是理想平整路面。 （3）一般車速常介于50～120km/h（即15～35m/s）之間。當車速在這個范圍時，在短波長路面，動載系數處于第二個峰值附近，動載系數較大；在長波長路面，動載系數卻處于第一個峰值和第二個峰值之間的波谷位置，動載系數較小。可見，基于減小動荷載的目的，應對路面不平整度的波長加以控制，尤其應控制變化幅度比較急劇的路面不平整形態。

2.4 路面波數譜密度與動荷載的關系

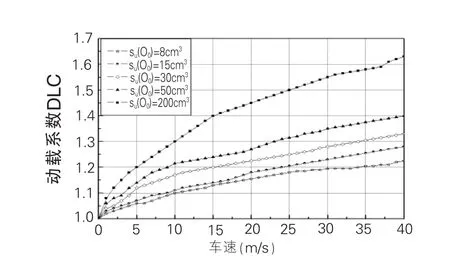
圖10 路面標準波數譜密度對動載系數的影響

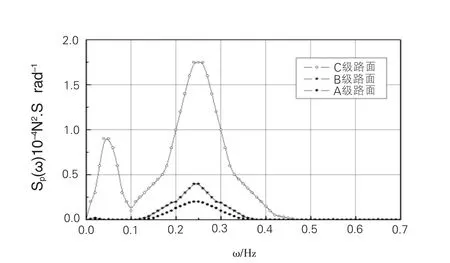
圖11 不同等級路面功率譜圖

當路面等級不同，即其標準波數譜密度不同時，在其激勵下產生的車輛動荷載有較大的差別，圖10表明了這種情況。圖中共繪出了五種標準路面波數譜密度條件下的動載系數變化趨勢， 當Su(ΩO)分別為8cm3，15cm3，30cm3時，分別表示了A級路面標準譜密度的下限、平均值和上限，Su(ΩO)分別為50cm3，200cm3時，分別表示了B級和C級路面。隨著車速的提高及路面質量（路面級別）的下降，動載系數迅速提高，特別對于C級路面，當車速提高到100km/h以上時，動載超載率達到55%以上，說明當車輛在該種路面上高速行駛時，空車相當于載重車，滿載車輛相當于超載車輛，這進一步印證了路面表面狀況與車輛隨機動載的鏈條關系，路面越糟糕，其承受的動態荷載越大。圖11中不同等級路面的動載功率譜密度比較圖也證實了這一規律。

3 結論

將路面不平度作為輸入激勵，采用數值分析方法能夠比較準確得出交通荷載與路面特性之間的關系。本文研究表明:

（1）路面不平度譜密度在低頻范圍內對車輛的激振能量最大，產生的動荷載也最大。

（2）車速對路面動載存在影響，但并不表現為動載隨車速的提高而提高，在某一車速下車輛發生共振，動荷載可以達到最大，高于和低于該車速動載都將減小。改變車速，短波長路面動載變異較小，長波長動載變異較大，說明車速對平整度差的路面影響較大，對平整度好的路面影響較小。

（3）動荷載的大小隨路面標準波數譜密度（路面等級）的變化而變化，路面等級越高，產生的動荷載越小，路面等級越低，產生的動荷載越大。

[1]任瑞波.瀝青路面結構計算方法與FWD應用技術的研究[D].哈爾濱:哈爾濱建筑大學博士學位論文，2000.

[2]王新明.路面表面特性與汽車動載研究[D].西安:長安大學碩士學位論文，2000

[3]鄧學鈞，孫璐著.車輛—地面結構系統動力學[M].北京:人民交通出版社，2000.

[4]Dave Crolla，喻凡.車輛動力學及其控制[M].北京:人民交通出版社，2004.

[5]GeertLombaert.Development and experimental validation of a Numerical model for the free field vibrations Induced by road traffic[D],2001.

[6]GB7031—86，車輛振動輸入路面平度表示方法[S].

[7]趙濟梅.路面平度譜分析應用研究報告[R].長春:長春汽車研究所整車研究室，1985.

[8]ISO8608.Mechanical vibration，road surface profiles.Reporting of measured data，1991.

[9]靳曉雄，張立軍，等.汽車振動分析[M].上海:同濟大學出版社，2002.

[10]朱位秋.隨機振動[M].北京:科學出版社，1993.