關于熵判據、亥姆霍茲函數判據和吉布斯函數判據的討論

王新平 王旭珍 王新葵 李醒龍 蔣晨然 任延煜

(大連理工大學化工與環境生命學部化學學院 遼寧大連 116024)

1問題的提出

無需環境做功，就可以發生的不可逆過程稱為自發性過程[1-3]。通過物理化學的學習，使學生能正確地判斷過程的自發性是很重要的，因為這是利用自發趨勢較大的過程生產目的產物和開發新能源，以及通過向系統輸入功的辦法使非自發過程實際進行的基礎。在物理化學學習中，能力較強的學生為了使自己所學的相應知識更加深入清晰，經常拿出不同物理化學參考書中的相關問題，讓教師答疑。本文提出的命題即來源于學生的下述問題：

“用由熵增原理得到的公式

ΔS隔離=ΔS系統+ΔS環境

判斷過程的自發性時，允許系統和環境之間有熱量交換，那么是否也允許它們之間有功的交換？”。

這是一個很難回答的問題，因為它涉及到原命題的正確性。筆者認為，這樣不太清晰的認識，可能會在一些大學的學生中普遍出現。為了更好地進行物理化學教學，值得在同行中對這個問題進行深入討論。

2 結果和討論

2.1 熵判據

首先必須強調的是，熵增原理，即所謂熵判據，并不能用于判斷過程的自發性。為便于對此確認，在這里先給出得到熵增原理的關鍵推導脈絡:

將卡諾定理推廣到有多個熱源、使用理想氣體為工質、每個無限小的過程都是卡諾循環中的可逆膨脹或可逆壓縮的情況時為:

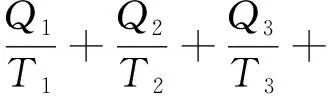
該循環過程表示為:

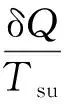
對于絕熱系統，可以推導得到:

ΔS絕熱(A→B)≥0 (>0，不可逆；=0，可逆)

這就是熵增原理。由上述熵增原理的推導過程，能夠得到以下兩點結論。

1) 一個不可逆過程可能是自發過程，也可能是非自發過程。所以，用熵增原理只能判斷絕熱條件下過程的可逆性，而不能判斷絕熱條件下過程的自發性。

2) 在熵增原理得出的推導過程中，并未涉及非體積功。因此，熵增原理應表述為：在絕熱和無非體積功的條件下，可逆過程會維持系統的熵不變；絕熱條件下的所有不可逆過程都是增熵過程，使系統的熵值變小的過程，是不可能實現的(即不能實際發生)。

下面的例題對于正確理解熵增原理很有幫助。

例題1:將物質的量為n，溫度為T1，體積為V1的理想氣體，在絕熱條件下壓縮到體積為V2。求在下列兩種壓縮方式條件下系統的熵變。

1) 以準靜態方式進行。

2) 用任意不可逆方式進行。

解:由熱力學第一定律，環境在絕熱條件下將系統壓縮時所付出的功全部轉化為系統的熱力學能。即理想氣體的溫度一定升高，而其最終溫度與環境所付出功的大小直接相關。

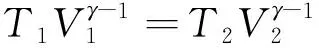
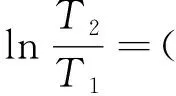
由理想氣體的熵變計算公式

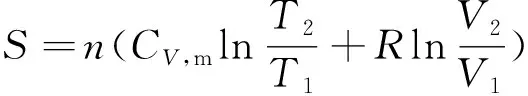
(1)

可得ΔS=0。

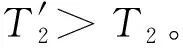
不可逆方式可以多種多樣，環境所付出功的大小不盡相同，相應使得熵變的大小也不同，但ΔS>0永遠成立。

環境做功將絕熱筒中的氣體(視為系統)壓縮，是一個典型的非自發過程。但是，它卻滿足ΔS絕熱(A→B)≥0的條件。這充分表明，熵增原理不能成為過程自發性的判據。但是，例題1這一典型實例，則支持熵增原理對于過程能否實際發生，以及以什么方式(可逆或不可逆)進行的判據。

上述例題表明，熵增原理并不排斥環境對系統做體積功的情況。

前述學生的問題，則是將熵增原理推廣到由實際系統和實際環境構成的虛擬系統，以便更廣泛地應用熵增原理的情況。

由于虛擬的隔離系統滿足絕熱條件,因此有：

ΔS隔離=(ΔS系統+ΔS環境)≥0 (>0，不可逆；=0，可逆)

(2)

顯然，在該虛擬的隔離系統內部，實際系統和實際環境之間熱和功的交換并不排斥式(2)的成立。也就是說，對于所研究的實際系統，無論它和環境之間熱和功的交換如何，只能實現(ΔS系統+ΔS環境)≥0的過程。能夠以不可逆方式實現的過程對應(ΔS系統+ΔS環境)>0；能夠以可逆方式實現的過程，其(ΔS系統+ΔS環境)=0。例題2則有助于深刻理解這一點。

例題2:抽出插板，讓與環境有良好接觸的溫度均為T、體積均為V1、物質的量分別為n1和4n1的O2和N2(可視為理想氣體)定溫混合(過程Ⅰ)，再將混合氣體定溫壓縮為V1(過程Ⅱ)(圖1)。① 用熱力學第二定律驗證過程Ⅰ的不可逆性。② 讓過程Ⅱ分別以不可逆和可逆的方式進行，驗證熱力學第二定律對過程可逆性判斷的正確性。

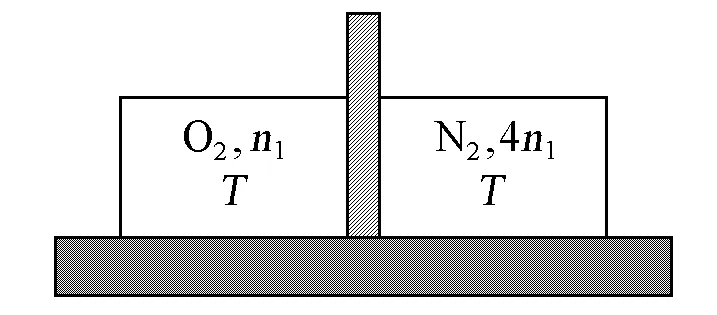
圖1 示意圖

解:

① 過程Ⅰ:

ΔSsy(Ⅰ)=ΔS(O2)+ΔS(N2)=5n1Rln2

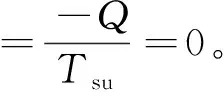
ΔS孤立(Ⅰ)=ΔS(Ⅰ)+ΔSsu(Ⅰ)= 5n1Rln2>0

則該氣體定溫混合過程為不可逆過程。

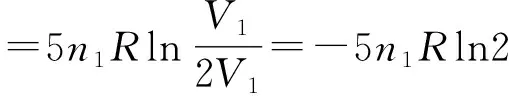
雖然系統的熵變為ΔSsy(Ⅱ)=-5n1Rln2，但環境的熵變依壓縮方式不同而不同。

該壓縮過程為理想氣體定溫過程，則ΔU=0，而Qsu=-Q=W。

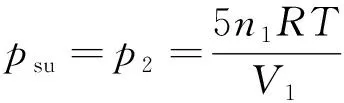
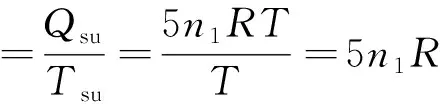
則：

ΔS孤立(Ⅱ)=ΔSsy(Ⅱ)+ΔSsu(Ⅱ)=5n1R(1-ln2)>0

所以，用熱力學第二定律可判斷該壓縮過程為不可逆過程。

2) 以環境的壓力始終極接近系統的壓力psu=p+dp≈p對系統加壓壓縮：

則:

ΔS孤立′ (Ⅱ)=ΔS(Ⅱ)+ΔSsu′(Ⅱ)≈-5n1Rln2+5n1Rln2=0

在例題2中，過程Ⅰ和過程Ⅱ以不可逆方式進行時，雖然它們均對應ΔS孤立(Ⅱ)=ΔSsy(Ⅱ)+ΔSsu(Ⅱ)>0，但前者是自發的不可逆過程，而后者卻是非自發的不可逆過程。這再次證明，用熱力學第二定律只能判斷過程進行的可逆性，而不能判斷過程的自發性。即(ΔS系統+ΔS環境)>0只能說明系統進行的過程能夠以不可逆方式實現。至于它是否自發發生，則無從判斷(無論從熵增原理的推導過程看還是從上述例題看，用熱力學第二定律判斷過程的自發性都是錯誤的)。該例題還表明，當系統和環境有功交換時，依據熵增原理仍能對過程的可逆性給出正確的判斷。

2.2 亥姆霍茨函數判據

亥姆霍茨函數判據，能夠用于判斷定溫、定容條件下過程的自發性。這可由以下推導過程得到確認。

由熱力學第二定律：

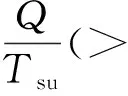
即：

Tsu(S2-S1)≥Q

在定溫條件下，T2=T1=Tsu,則:

T2S2-T1S1≥Q

又:

Q=ΔU-W

于是有：

-((U2-T2S2)-(U1-T2S1))≥-W

(3)

即：

-ΔAT≥-W(>，不可逆；=，可逆)

如過程不僅定溫而且定容，則體積功WV=0,于是有：

-ΔAT，V≥-W′(>，不可逆；=，可逆)

(4)

若非體積功W′為0，則過程的功W=0。這就是說，此時系統和環境間完全沒有功的傳遞，此時的不可逆過程，就是嚴格意義上的自發過程。因此，式(4)變為:

ΔAT，V≤0(<0，自發；=0，可逆)

(5)

這就是亥姆霍茨函數判據。

由以上亥姆霍茨函數判據的導出過程可以看出，用它來判斷過程的自發性才是科學的。在定溫、定容、W′=0的條件下，ΔAT，V<0的過程自發地進行；而ΔAT，V=0的過程，實際則處于平衡狀態。依據狀態函數的性質，在定溫、定容且W′=0的條件下，一個ΔAT，V>0的過程，其逆向過程一定為ΔAT，V<0。因此，ΔAT，V>0的過程是非自發的，即其逆向過程自發地進行。

這里必須強調的是，亥姆霍茨函數判據的應用不應僅僅限于對過程自發性的判斷，而更應在于其下述應用：

1) 判斷利用自發過程，在定溫、定容條件下環境可獲取的最大非體積功。

對于一個定容條件下的自發過程(其ΔAT，V<0)，由式(4)可知，只要滿足-ΔAT,V≥-W′，則過程就是可以實現的。即，封閉系統在定溫、定容過程中，對環境能做的最大功(自發沿可逆途徑進行)等于系統亥姆霍茨函數的減少。該式可為探尋開發獲取定容條件下的新能源給出重要的啟示。

2) 判斷要實現一個定溫、定容條件下的非自發過程，環境至少必須付出的非體積功。

將式(4)變為：

ΔAT,V≤W′(<，不可逆；=，可逆)

(6)

式(6)表明，對于一個定容條件下的非自發過程(其ΔAT，V>0)，只要環境為其做非體積功等于或超過系統的亥姆霍茨函數變ΔAT，V，則仍可使該過程可逆或不可逆地實現。雖然在定容條件下的過程不多，但實際生活中并不乏這樣的實例。如，給封閉的手機電源充電。

2.3 吉布斯函數判據

用吉布斯函數判據可判斷在定溫、定壓條件下過程的自發性，同樣可由其推導過程得到確認。

如過程在定溫、定壓下進行，有：

W=WV+W′=-psu(V2-V1)+W′=-p2V2+p1V1+W′

則式(3)可寫為：

-((U2+p2V2-T2S2)-(U1+p1V1-T1S1))≥-W′

上式即：

-ΔGT,p≥-W′(>，不可逆；=，可逆)

(7)

在定壓條件下，系統的體積膨脹或縮小時，雖然涉及定壓體積功，但那是維系定壓條件的自然結果，不是人為地通過壓力差注入的體積功[3]。因此，在定溫、定壓下，W′=0的不可逆過程即自發過程。于是有：

ΔGT,p≤0(<0，自發；=0，可逆)

(8)

式(8)即為吉布斯函數判據。該判據表明，在定溫、定壓且W′=0的條件下，如ΔGT,p<0，則過程自發發生；如ΔGT,p>0，則相應過程為非自發過程；如ΔGT,p=0，則系統處于平衡。

同亥姆霍茨函數判據類似，吉布斯函數判據的應用也不應僅僅限于對過程自發性的判斷，而更應在于其下述應用：

1) 判斷利用自發過程，在定溫、定壓條件下環境可獲取的最大非體積功。

對于一個定壓條件下的自發過程(其ΔGT，p<0)，由式(7)可知，只要滿足-ΔGT,p≥-W′，則過程就是可以實現的。即，封閉系統在定溫、定壓過程中，系統對環境能做的最大非體積功(自發沿可逆途徑進行)等于系統吉布斯函數的減少。式(8)可為探尋開發獲取定壓條件下的新能源給出重要的啟示。例如，探尋利用新反應的高能燃料電池。它表明，要通過化學反應獲取更多的非體積功(如電能)，必須把目光瞄向那些ΔrGm,T,p值為負且其絕對值更大的反應。

2) 判斷要實現定溫、定壓條件下的一個非自發過程，環境至少必須付出的非體積功。

將式(7)變為：

ΔGT,p≤W′(<，不可逆；=，可逆)

(9)

式(9)表明，在定溫、定壓下，一個非自發過程并非不能實現。只要環境對系統所做的非體積功大于封閉系統中該過程吉布斯函數的改變量，就可以實現。例如水的電解、植物的光合作用等。顯然，式(9)對于利用現有能源，開發新的反應途徑或新產物給出了重要啟示。

3 結論

熵判據、亥姆霍茲函數判據和吉布斯函數判據是化學熱力學中很重要的3個判據。準確靈活地應用亥姆霍茲函數判據和吉布斯函數判據判斷過程的自發性，目標準確地利用自發反應開發高效新能源，有效地利用現有能源開發非自發過程是化學熱力學的重要核心內容。筆者認為，在物理化學教學中，應避免對第一個判據的誤用。同時，也應強化后兩個判據的外延。這樣，才能使相應內容與電化學、光化學內容構成暢通的知識體系，有利于學生掌握貫通的物理化學知識，培養學生創新能力。

參 考 文 獻

[1] 胡英，呂瑞東，劉國杰，等. 物理化學.第5版.北京:高等教育出版社，2007

[2] 傅獻彩，沈文霞，姚天揚，等.物理化學.第5版.北京:高等教育出版社，2008

[3] 劉俊吉，周亞平，李松林.物理化學.第5版.北京:高等教育出版社，2009