曲面筆式加工刀位點曲線的實時擬合*

孟書云

(南京工程學院自動化學院，江蘇南京211167)

復雜曲面常規加工是將刀位點軌跡處理成大量直線或圓弧組成的加工代碼，由CNC系統內簡單曲線插補功能，生成控制指令來驅動伺服系統。這會使加工代碼量巨大，機床需頻繁加減速以及出現加工表面不光順等問題［1－3］。

為避免上述問題，Yang等提出了基于離散刀位點的復合刀具路徑生成方法［4］;Kang等給出了基于最小二乘法的采用B樣條精確擬合刀位點軌跡的方法［5］;上述方法未提及離散刀位點的來源，同時為達到擬合的高精度，需進行迭代計算，運算量較大，存在迭代不收斂的可能性。Zhao等利用B3數學模型實現了數控加工刀位點軌跡規劃，在反求控制定點時涉及求取邊界切矢，而擬合曲線對邊界條件敏感，選取不當會使擬合曲線畸變［6］;Chen等面向三角網格曲面提出了圓弧樣條刀軌生成方法，但僅局限于三角片型曲面的刀路規劃［7］。

針對復雜曲面筆式加工，提出一種刀位點軌跡實時高精度生成算法:根據插補器中讀入的曲面、刀觸點等幾何信息以及刀具、加工余量等工藝信息，用三次B樣條曲線實時重構刀位點軌跡線，來高精度逼近理想刀位點軌跡。

1 曲線數學模型

曲面筆式加工以曲面局部區域為加工對象，即刀具路徑在指定的曲面局部加工區域上進行規劃。以曲面上某一點的法矢量作為投影方向，將一族空間自由曲線作平移旋轉變換，使投影后的一系列曲線能正好落在曲面待加工的局部區域上。

如圖1所示，以三次B樣條方法描述的初始導引線P(m)，經旋轉平移變換后，再繞曲面在投影處法矢量旋轉，得到目標導引線Q(m)。

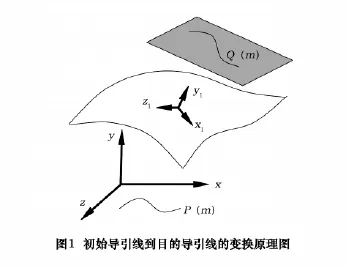
將目標導引線Q(m)沿曲面上投影點的法矢量映射，最終投影在曲面上的曲線才是實際加工時的刀觸點跡線。復雜曲面多采用參數形式描述，故提出的算法以參數式曲面作為研究對象，表示為2個變數u、v的單值函數S(u，v)。設單位投影矢量為O，其刀觸點跡線可表示為

其中:F(m，n)為由目的導動線形成的參數式導動曲面;m、n為該曲面的2個參數(a≤m≤b，－∞ ＜n＜+∞)，并以三次B樣條方法描述的參數式曲面S(u，v)作為筆式加工的對象;di，j為曲面的控制頂點;s、t分別為參數u和參數v方向上的控制頂點數。

2 刀位點數據的獲取

由式(1)可看出，刀觸點跡線由待加工曲面和一族導動曲面的交線族組成。由于待加工曲面和導動曲面的數學描述都是關于參數的高次耦合表達式，故無法直接得到交線的數學表達式。

為此，從目的導引線出發，據其和刀觸點跡線之間的幾何和運動學關系，找到兩者之間的聯系。由于目的導引線與初始導引線之間存在一一映射的關系，故初始導引線和曲面上的自由曲線型刀觸點跡線之間亦存在一一對應關系。

如圖2所示，目的導引線Q(m)和刀觸點軌跡線L(u)是一對空間曲線偶。當加工的刀具沿L(u)運動到某點A時，在目的導引線Q(m)上必存在唯一一點B與之相對應，將點A和點B稱為點偶。

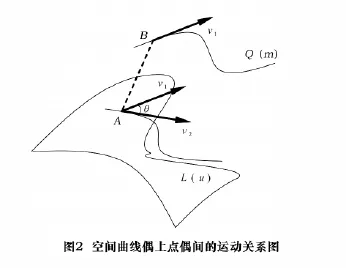
設刀具在刀觸點跡線(即S(u，v)和F(m，n)交線)A處速度為v2，而目的導引線上對應點B處速度為v1，兩速度矢量之間的夾角為θ，則

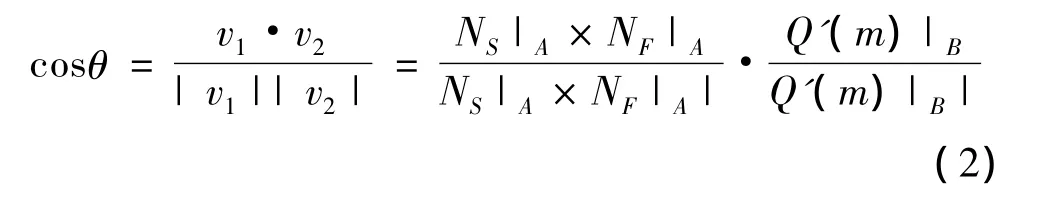
其中NS|A和NF|A分別表示曲面 S(u，v)和 F(m，n)在點A處法矢量;Q′(m)|B表示目的導引線在點B處的切矢量。

設插補進給速度為V，時間用t表示，由于時間增量非常小，故可以將兩參數曲面交線的弧長ds對時間的微分近似為插補進給速度，即

刀具沿該刀觸點跡線加工時，若保持刀觸點速度的恒定，就能保證恒定的材料去除率，有利于曲面加工質量的提高。

為簡化計算，將速度矢量v1和v2及兩者夾角θ構成的一般三角形近似為直角三角形，則

而目的導引線Q(m)上的微段曲線關于時間t的一階導數，有:

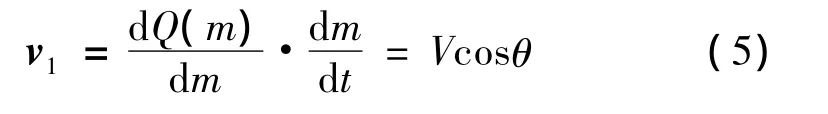
同理可求出參數m關于時間t的二階導數。

從初始導動曲線P(m)(a≤m≤b)出發，考慮該曲線關于插補周期Δt的Taylor展開式。設曲線上當前點對應的參數值為mk，下一點對應的參數值為mk+1，則

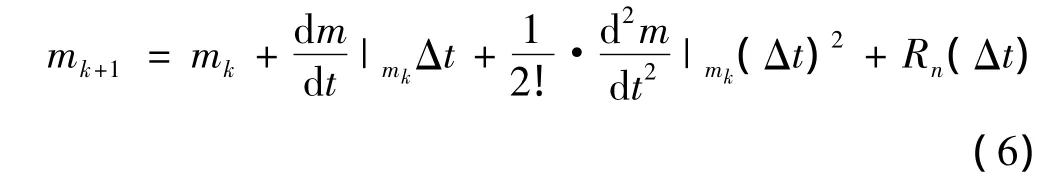
其中:Rn(Δt)是Taylor展開式的高次項。當曲線P(m)的曲率不是很小時，可以將mk+1的值只取至一次項。至此，求出了刀觸點軌跡線上相鄰刀觸點在初始導引線上對應點的參數值。

將式(6)求得的參數值代入式(1)，可反求出刀觸點跡線的點在曲面上對應的(u，v)值，進而得到該點的坐標值。

目前大多數數控系統具有刀補功能，可直接用刀觸點坐標插補加工，但當加工自由曲面類零件時，直接用刀補功能將產生較大的誤差，需計算刀心軌跡，故需根據上述有序離散刀觸點及曲面、刀具等工藝信息，得到一組有序離散刀位點，進而完成刀心軌跡的計算。

3 刀位點軌跡實時高精度構造

在刀位點序列(已剔除產生干涉的刀位點)中每隔一個時間段順次取出4個點，分段擬合理想刀位點軌跡線。每次擬合計算以連續4個刀位點作為輸入。如圖3所示，為提高刀位點軌跡擬合精度，采取“去兩邊，取中間”的策略，使用三次B樣條曲線作為擬合曲線數學模型，即連續4個刀位點Pi(i=0，1，…，3)可反求出6個控制頂點，其決定的曲線如圖3中細實線所示(首末控制頂點分別為P0、P3，其余控制頂點di(i=1，…，4)用“Δ”表示)。

每順序4個控制頂點決定一個節點區間上的曲線段。生成的3段三次B樣條曲線段，保留中間一段，即控制頂點di(i=1，…，4)生成的曲線段，作為對刀位點數據P1、P2之間理想刀位點軌跡線的擬合。對于刀位點P2、P3之間的理想刀位點軌跡，由過 Pi(i=0，1，…，3)的三次B樣條曲線擬合，保留位于P2、P3之間的曲線段，依此類推。

在對刀位點數據進行擬合時，有兩個問題需要解決:一個是如何進行準確的參數化得到合適的節點矢量;另一個是如何確定恰當的邊界條件作為補充條件，用于控制頂點的求取。

顯然，這些有序刀位點數據確定的理想刀位點跡線的弧長是個未知量。由文獻［8］可知，利用通過相鄰刀位點且弦高為δ(即刀心軌跡的加工精度)的圓弧段弧長來近似理想刀位點跡線的弧長，即使用近似圓弧法參數化方法，比使用均勻節點法、向心法和累積弦長法要更加精確。

設相鄰刀位點Pi、Pi+1的連線長度為L，則近似圓弧段的圓弧半徑為

圓弧弧長S為

為保證擬合的三次B樣條曲線通過給定的4個連續刀位點 Pi(i=j，j+1，…，j+3)，以近似圓弧參數化法求得的參數矢量，需在參數區間端點設置重節點并進行歸一處理。

設輸入的4個刀位點數據為Pi(i=0，1，…，3)以及單位切矢量˙Pi(i=0，…，3)。由樣條曲線性質可知，有6個控制頂點di(i=0，1，…，5)待求，而歸一化后的節點矢量為 U=［0，0，0，0，u4，u5，1，1，1，1］，其中

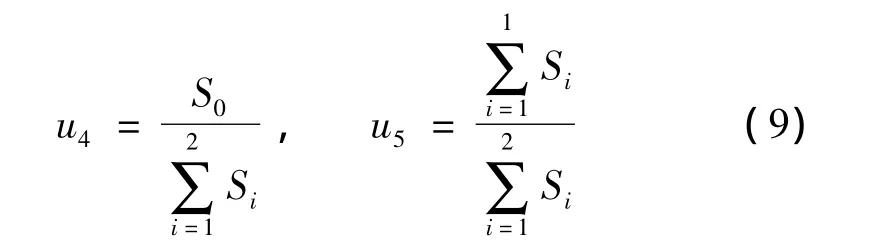
每次計算，僅需更新u4、u5即可。

對于本問題，求解用于擬合的三次B樣條曲線控制頂點的方程組可表示為

其中:Ni，3(ui)(i=0，1，…，3)是節點區間端點處的三次四階B樣條基函數。由基函數遞推公式可知，非零值共3個，由于采用了近似圓弧參數化，每個基函數的值需實時計算。

由已知條件得知式(10)解不確定，需再補充2個條件，擬通過曲線兩端切矢條件建立邊界約束。由刀觸點跡線和刀心軌跡的形成過程可知，用于擬合的三次B樣條曲線，在每個有序離散刀位點處的切矢方向是可求的，但模長不易確定，而不恰當的模長通過反求得到的刀心軌跡存在畸變的可能［9］。

根據曲線的微分幾何理論［10］，曲線的弧長是自身的不變量，選取弧長作為參數來描述曲線，有使曲線上每一點處切向量為單位向量的性質。而近似圓弧參數化方法可以使得擬合的曲線上每一點的切矢量近似為單位切矢。

由于節點矢量U={ui}，i=0，…，9，假設算子=ui+j－ui，而刀心軌跡L(u)在指定參數處的切矢量分別為

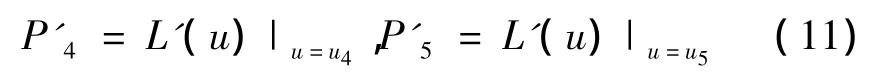
則補充的兩個條件為

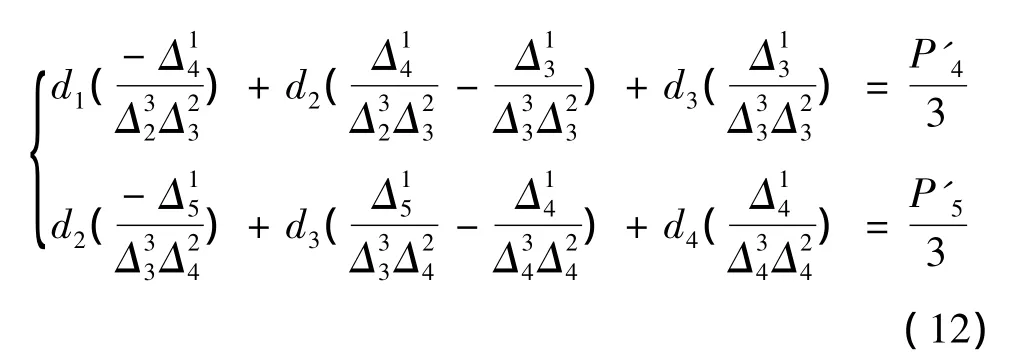
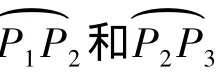
4 實例分析

研究測試加工對象如圖4所示，被加工曲面采用三次B樣條方法描述，曲面控制頂點坐標數據列于表1中，長寬高分別為120 mm×120 mm×55 mm。

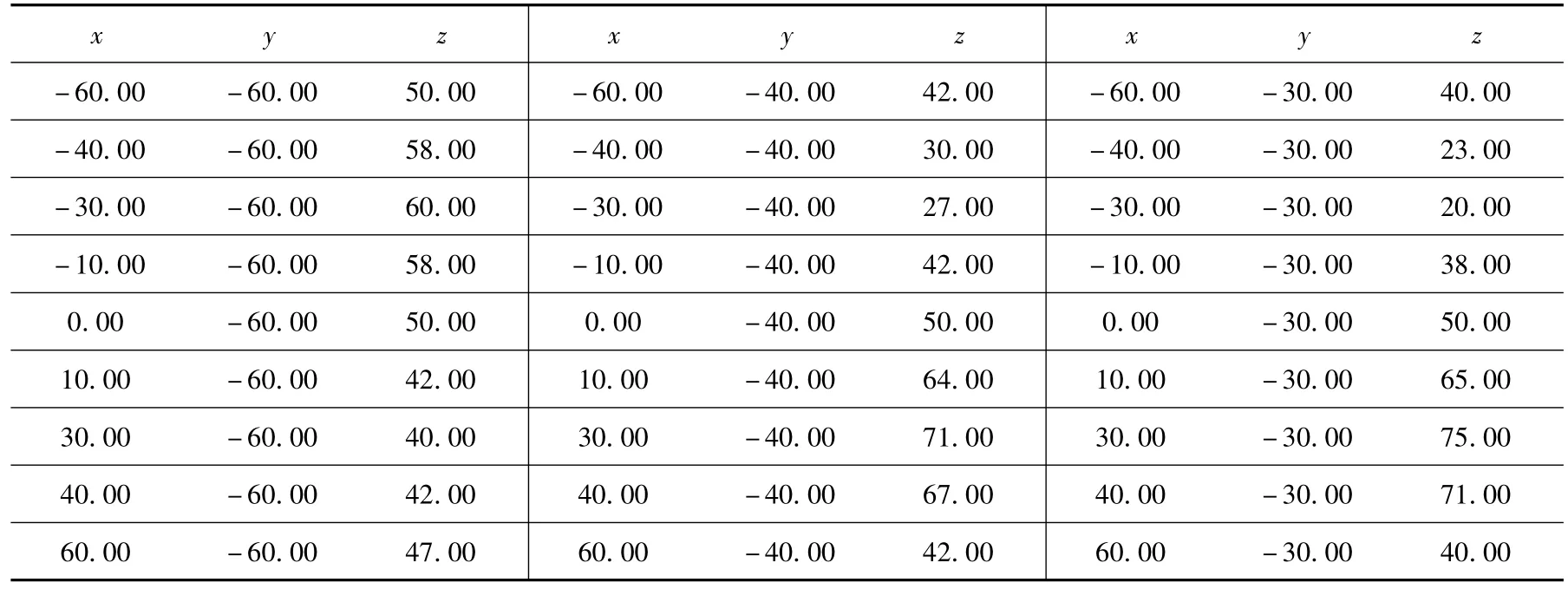
表1 曲面部分控制頂點坐標數據表 mm

設定加工進給速度為3 000 mm/min，插補周期為8 ms。將平面上的梅花和字符組成的組合圖案，經平移旋轉變換調整到合適的狀態，投影到該曲面上，生成刀觸點軌跡如圖4所示。部分刀觸點相關數據列于表2中。以刀頭直徑為3 mm的球頭刀為加工刀具，沿刀觸點處曲面外法矢量方向作為偏置方向，得到有序的離散刀位點數據系列。

表2 部分刀觸點相關數據表 mm

在CPU主頻為1.66 GHz，內存為1 M的硬件環境以及Windows XP操作系統環境下，基于Visual C++6.0軟件開發平臺，由給出的算法對有序離散刀位點進行三次B樣條曲線逐段擬合，每4個刀位點反求6個控制頂點所需時間列于表3中，平均用時0.014 ms。

表3 離散刀位點反求所需時間表 ms

與傳統的大量連續直線段作為刀心跡線相比，采用三次B樣條曲線擬合刀位點跡線帶來的曲面輪廓誤差如圖5所示。

因三次B樣條擬合嚴格通過所給定的刀位點，故加工時在這些點是沒有誤差的。與直接將離散刀位點順序連接形成的直線段作為刀心跡線相比，采用三次B樣條擬合刀心跡線，弓高誤差明顯減小。

5 結語

文中探討了復雜曲面筆式加工時，使用三次B樣條曲線實時高精度逼近理想刀位點軌跡的算法。算法的實現有利于對自由曲線軌跡進行高精度控制，大幅減少了加工代碼量和內存占用量，為自由曲面的高精密加工奠定了理論基礎。關于實時剔除會產生干涉的刀位點的算法，仍以順次4個刀位點為一組進行實時干涉分析，待另撰文詳述。

［1］SUN Yuwen，GUO Dongming.Iso－parametric tool path generation from triangular meshes for free － form surface machining［J］.The International Journal of Advanced Manufacturing Technology，2006，28:721 －726.

［2］CHRISTOPHE Tournier，EMMANUEL Duc.Iso－ scallop tool path generation in 5 － axis milling［J］.The International Journal of Advanced Manufacturing Technology，2005，25(9/10):867 －875.

［3］楊長祺，秦大同，石萬凱.自由曲面五軸等殘余高度高精度加工的路徑規劃［J］.計算機輔助設計與圖形學學報，2003，15(5):621－626.

［4］楊旭靜，楊欽文.基于離散刀位點的復合刀具路徑生成方法研究［J］.湖南大學學報:自然科學版，2009，36(9):35 －39.

［5］康書杰，周來水，張綠禮，等.數控刀位點的B樣條精確擬合［J］.機械工程與自動化，2007(141):95－97.

［6］趙艷春，張金萍，王丹，等.基于B3樣條曲線的數控加工刀位軌跡計算的研究［J］.沈陽化工學院學報，2009，23(2):147 －149，169.

［7］陳曉兵，廖文和，吳海兵，等.三角網格表面數控加工圓弧樣條刀軌研究［J］.中國機械工程，2009，20(14):1642 －1646.

［8］陽春啟，楊旭靜，王伏林.刀位點曲線擬合中的近似弧長參數化方法［J］.湖南大學學報:自然科學版，2008，35(8):34 －37.

［9］孟書云.高精度開放式數控系統復雜曲線曲面插補關鍵技術研究［D］.南京:南京航空航天大學，2006.

［10］劉根洪，何仁杰.微分幾何與計算幾何［M］.成都:四川大學出版社，2000:18－23.