多元多峰值目標函數在MATLAB中的優化

姚運萍 ，王倩倩

（1.蘭州理工大學 數字制造技術與應用省部共建教育部重點實驗室，甘肅 蘭州730050；2.蘭州理工大學 機電工程學院，甘肅 蘭州730050）

多元多峰值函數[1-2]在定義域內有多個局部極值點，許多傳統的優化方法都是單點搜索，這種點對點的搜索方法，對于多元多峰值函數的搜索空間常常會陷入局部的某個單峰的極值點。相反，遺傳算法同時對群體中多個個體進行并行處理[3]，即同時對搜索空間中的多個解進行評估，在搜索過程中能以很大的概率找到全局最優。遺傳算法提供了一種求解非線性、多模型、多目標等復雜系統優化問題的通用框架，它不依賴問題領域的具體性，已廣泛應用于眾多工程領域，用以解決多變量、多目標、多峰值等約束的優化問題。

1 遺傳算法

1.1 遺傳算法的優點

(1)遺傳算法采用不確定性規則，強調利用概率轉換規則[4]來引導搜索過程；

(2)遺傳算法隨機產生多個初始點，通過選擇、交叉和變異三種遺傳操作產生下一代種群；(3)遺傳算法具有較高的搜索能力和極強的魯棒性；(4)遺傳算法采用概率的變遷規則來指導其搜索方向[5]，對一個被編碼的參數空間進行高效搜索；

(5)遺傳算法是一個多學科相結合與滲透的產物，其研究方向極其廣泛。

1.2 遺傳算法運算流程

完整的遺傳算法的運算流程可以用圖1來描述。可以看出，使用上述三種遺傳算子（選擇、交叉和變異）的遺傳算法的主要運算過程如下：

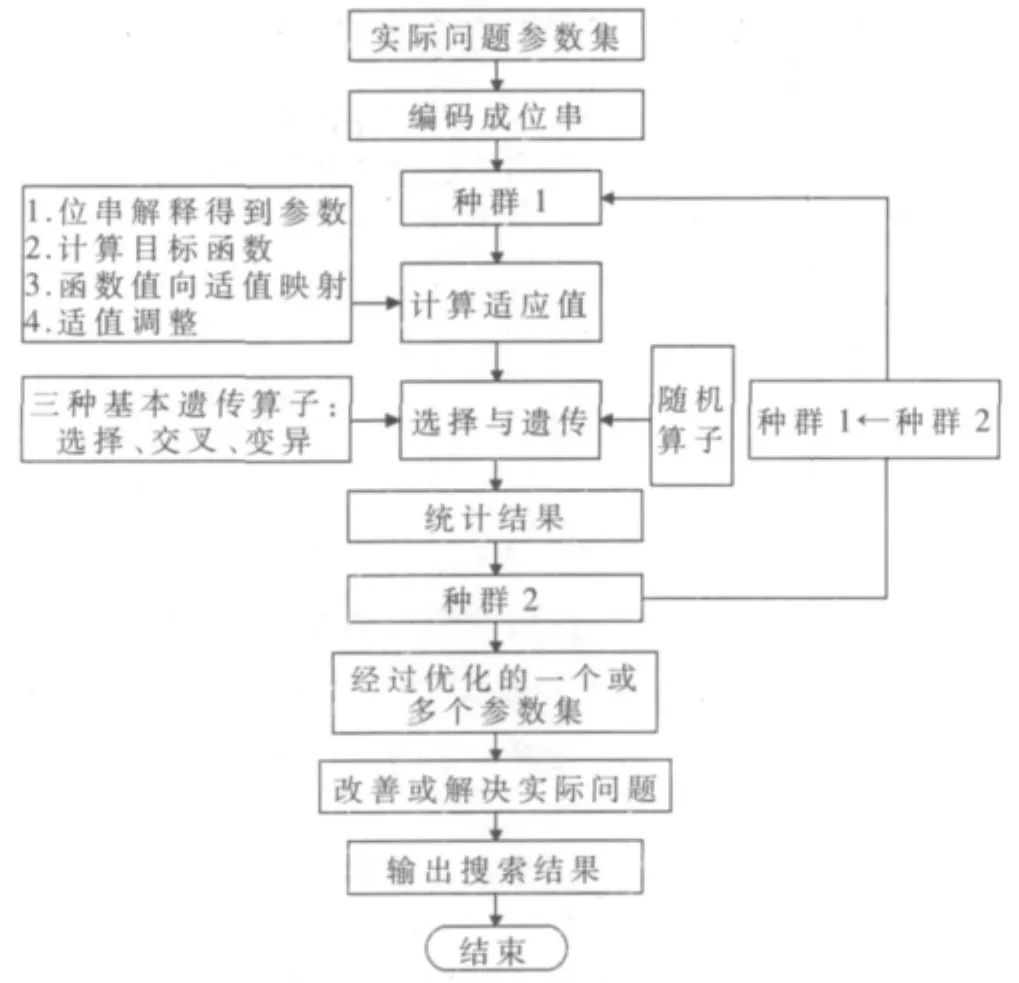
圖1 遺傳算法運算流程圖

(1)編碼：遺傳算法在進行搜索之前先將解空間的解數據表示成遺傳空間的基因型串結構數據，這些串結構數據的不同組合就構成了不同的點。

(2)初始群體的生成：隨機產生N個初始串結構數據，每個串結構數據成為一個個體，N個個體構成一個群體。設置進化代數計算器t(t＞0)和最大進化代數T。

(3)適應度值評價檢測：根據具體問題，計算群體P(t)中各個個體的適應度。

(4)對群體中的個體施加遺傳操作：將選擇、交叉和變異三種遺傳算子作用于群體，實現群體內個體結構的重組處理。

(5)終止條件判斷：若 t≤T，則 t←t+1，轉到步驟(2)；若t＞T，則以進化過程中所得到的具有最大適應度的個體作為最優解輸出，終止運算。

2 基于MATLAB遺傳工具箱的多元多峰值優化

遺傳算法工具箱使用MATLAB矩陣函數為實現廣泛領域的遺傳算法建立了一套通用工具，這個遺傳算法工具是用M文件寫成的命令行形式的函數，是完成遺傳算法大部分重要功能的程序集合[6-8]。

MATLAB遺傳工具箱主要參數含義：

(1)“@fitnessfcn”：計算適應度函數值的M文件的函數句柄；

(2)“nvars”：適應度函數中獨立變量的個數；

(3)“x”：最終值的到達點；

(4)“fval”：適應度函數在 x 點的值；

(5)“reason”：算法停止的原因（可選項）；

樞紐錨固是在對外客運樞紐布局的基礎上，充分發揮城市交通網絡的功能，如道路、軌道交通等。在對外客運樞紐設計中，發揮錨固區域交通網絡的作用，如高速公路、干線公路、城際公路、鐵路以及公路客運班線等。因此，城市綜合客運樞紐的錨固能夠為人民群眾出行的便捷性提供保障。

(6)“output”：包含關于算法在每一代性能的結構體（可選項）；

(7)“population”：最后種群（可選項）；

(8)“option”：一個包含遺傳算法選項參數的結構體(可選項)。

如果不設置選項函數，則遺傳算法使用其本身自帶的缺省選項值。該參數結構體的自帶默認值分別為：種群規模為 20，最大代數為 100，選擇概率為 0.8，交叉概率為0.5，變異概率為0.2。也可通過gaoptimset函數改變默認值，以達到使用者的需求。

3 多元多峰值函數優化實例

目標函數及函數的約束條件：

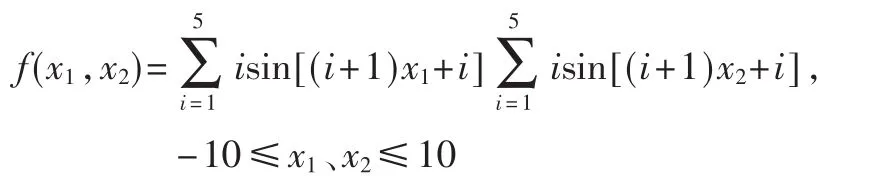
圖2所示為目標函數的函數圖像。

圖2 目標函數圖像

遺傳算法顯示結果如下：

（1）經過10次迭代后的目標函數值如圖3所示。此時，x1=-6.785 1，x2=-7.426 8，minf(x)=-176.621 1。

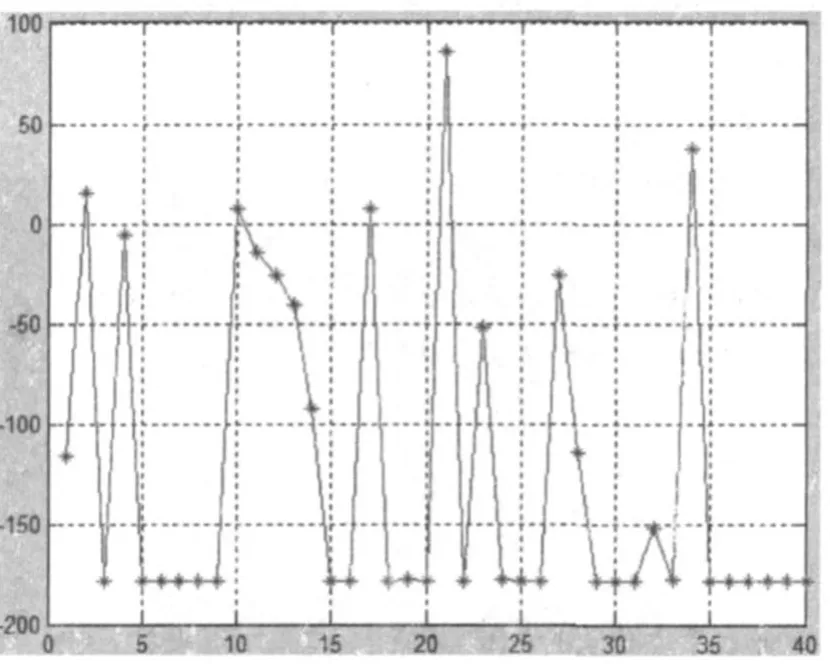
圖3 經過10次迭代后的結果

（2）經過50次迭代后的目標函數值如圖4所示。此時，x1=-6.774 6，x2=-7.397 3，minf(x)=-178.519 1。

（3）經過50次迭代后，種群目標函數均值的變化和最優解的變化如圖5所示。

本文采用基于MATLAB的遺傳算法，利用強大的數學計算能力和遺傳工具箱，在全局搜索空間內尋找極值點，能夠有效地對多元多峰值函數進行優化，避免了利用傳統優化方法在多元多峰值函數優化過程中陷入局部極值點的優化誤區。使用者可以避免維護遺傳算法種群和染色體的數據結構的繁重編程工作，節省了大量編程時間和精力，將精力集中在遺傳算法的改進和具體問題的應用中。

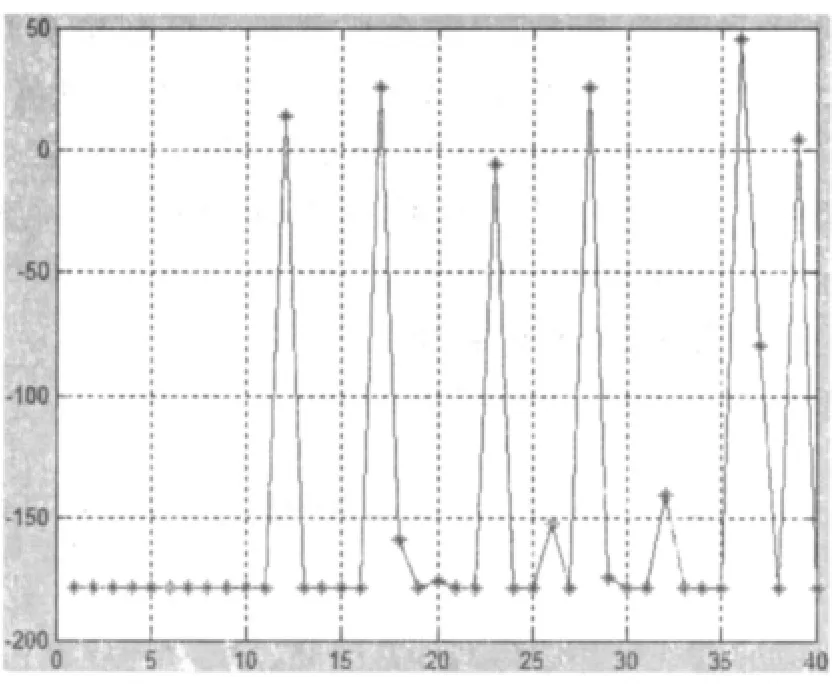
圖4 經過50次迭代后的結果

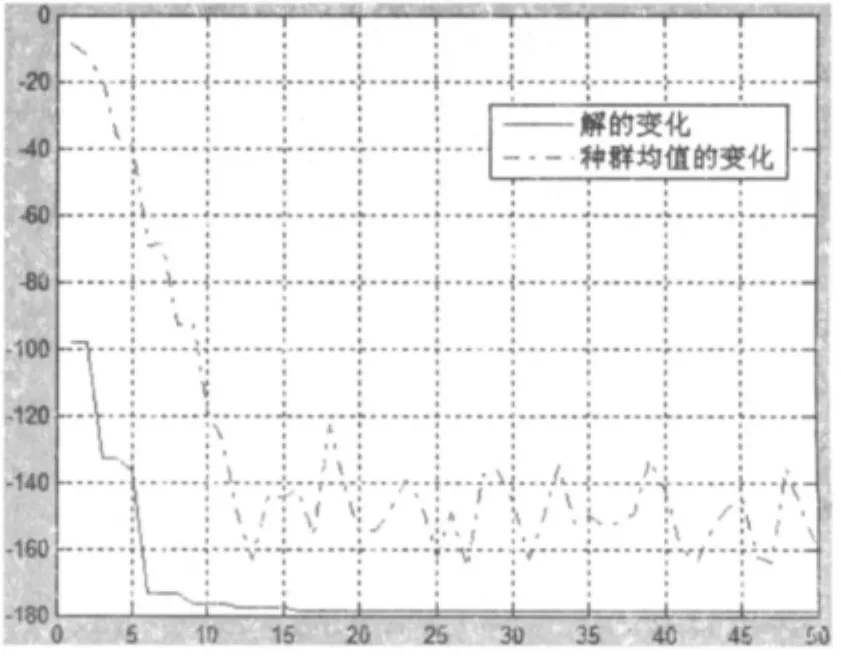
圖5 經過50次迭代后種群目標函數均值的變化和最優解的變化

[1]李敏強，寇紀淞，林丹，等.遺傳算法的基本理論與應用[M].北京：科學出版社，2003.

[2]孫小軍，趙天緒，焦建民.多峰極值優化問題的算法性能分析和比較[J].昆明理工大學學報(理工版)，2009，34(5)：104-107.

[3]劉道華，原思聰，鄔長安，等.面向對象的改進遺傳算法優化設計[J].華中科技大學學報(自然科學版)，2008，36(7)：89-92.

[4]張曉偉，劉三陽，遲曉妮.高效求解多峰值全局優化的區間-遺傳算法[J].吉林大學學報(工學版)，2008，38(4)：876-879.

[5]黃江波，付志紅.基于自適應遺傳算法函數優化與仿真[J].計算機仿真，2011，28(5)：237-240.

[6]雷英杰，張善文，李續武，等.MATLAB遺傳算法工具箱及應用[M].西安：西安電子科技大學出版社，2005.

[7]劉文強，張曉偉.多峰值全局優化的混合算法[J].計算機工程與應用，2008，44(3)：43-45.

[8]王社科.機械優化設計[M].北京：國防工業出版社，2007.