Lagrange定理輔助函數的構造
2012-09-29 08:48:28未霞飛鄧偉娜
時代農機 2012年1期
未霞飛,鄧偉娜
(黃淮學院 數學科學系,河南 駐馬店 463000)
1 分析法
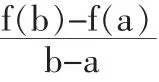
2 嘗試法
嘗試法的基本思想方法是:設函數f(x)滿足Lagrange定理的條件,在f(x)的基礎上再加上一個函數g(x)(嘗試函數),使得和函數 Ф(x)=f(x)+g(x)滿足 Rolle 定理的條件,從而達到證明Lagrange定理的目的。
構造輔助函數如下:
3 幾何法
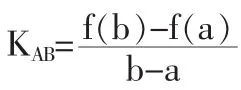
顯然,Φ(x)滿足羅爾定理的條件,即為所求輔助函數。
任取弧AB上一點C,其坐標為(x,f(x)),考慮以C及曲線兩端點A,B為頂點的三角形的面積,可設輔助函數顯然,Φ(a)=Φ(b),且Φ(x)滿足羅爾定理的其他條件,即為所求輔助函數。
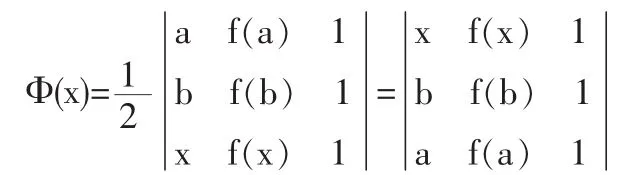
根據幾何意義構造輔助函數,來證明定理和命題,是一種非常直觀,易于接受的方法。
[1]鄧樂斌.拉格朗日中值定理輔助函數的構造方法[J].鄖陽師范高等專科學校學報,2005,(3):6-9.
[2]費定暉,周學圣編.數學分析習題集(三)[M].濟南:山東科學技術出版社,1980.
[3]謝效訓.關于拉格朗日中值定理的證明[J].高等數學研究,2001,(9):33—34.
[4]華東師范大學數學系.數學分析:上冊[M].北京:高等教育出版社.2001.

