干摩擦力學系統的建模及振動響應分析
汪 俊WANG Jun
(廣州城市職業學院 信息與汽車工程學院,廣州 510405)
0 引言
干摩擦廣泛存在于機械系統的摩擦副中,如金屬絲減振器,金屬橡膠元件,車輛中離合器的主動盤與從動盤的摩擦面中,如圖1所示。其減振的頻帶寬,可有效的降低系統的振幅,是一類行之有效的被動隔振和減振裝置,因此得到了工業界的廣泛關注。

圖1 離合器中的干摩擦交接面
由于干摩擦力學特性的強非線性(如回復力與位移曲線呈遲滯特性),使得干摩擦元件的設計較為困難,通常依靠經驗或大量的試驗試制等手段進行設計,成本高,周期長。為此,建立合理的干摩擦力學模型和推導計算量適當的數值方法就顯得尤為重要。至上世紀三十年代以來,國內外眾多學者對此展開了大量研究。
Den.Hartog在1931年提出了理想的干摩擦模型(coulomb模型)。假設一物體在干摩擦交接面上運動,干摩擦阻力總是阻礙運動,因此,干摩擦力的方向總與運動方向相反,但其大小不變。從時域上看,干摩擦阻力的波形為方波,其變化規律可表示如下:
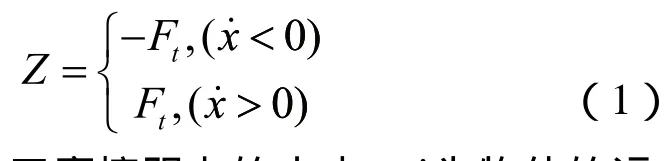
其中,Ft為干摩擦阻力的大小, 為物體的運動速度。
Den.Hartog的模型表達了理想的干摩擦。然而,大量的實驗研究表明,物體與干摩擦表面相接觸時,物體速度方向的改變并不是突然發生的,而是存在一個過渡過程。由于接觸面本身有一定的彈性,在外力的作用下,造成了接觸面有一定的彈性變形。當外力的方向改變時,物體的運動方向并沒有立刻改變,當外力的大小增大到一定程度,物體與接觸面才產生相對位移。
考慮到接觸面的彈性性質,Iwan在1961年提出了著名的雙折線遲滯模型,該模型將干摩擦阻力看成一根彈簧和一個標準的coulomb摩擦副串聯,且能更好的表達干摩擦阻力的非線性性質。
本文針對一個含有干摩擦元件的單自由度系統,實測了其在諧波激勵下出現的粘滑運動,并將計算值與實測值進行了對比。結果表明,文中給出的建模和計算方法是有效的。
1 單自由度干摩擦系統的實驗研究
測試對象為一含干摩擦的單自由度系統,圖2為測試原理圖。由MTS的作動端對物體施加垂直方向的位移激勵x (t)=x0+xmsin (2π ft),其中,f為激勵頻率(Hz),xm為激勵幅值(mm),x0(mm)為預載。圖2中,OA所示的位置是初始位置。在預載x0的作用下,OA由初始位置運動至水平位置OB,然后在水平位置OB附近作往復擺動。
假設在位移激勵Δx下,OB運動到了OC。假設OA的長度為l,則的擺角為:

圖3為時間-擺角關系的測試結果,可見單自由度系統時間—擺角呈現明顯的粘-滑運動。

圖2 單自由度運動響應測試原理
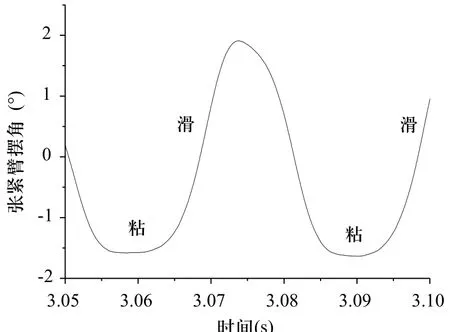
圖3 單自由度系統的粘-滑運動
2 單自由度干摩擦系統的力學模型
研究對象為圖3所示的振動系統。該系統由兩輪、一帶和一個集中質量組成。其中,集中質量連接彈簧k (N/m),阻尼c (Ns/m),集中質量受到幅值為P (N)、頻率為ω (rad/s)、相位為0度的激勵力作用。假設集中質量與帶之間的摩擦為干摩擦,則該集中質量的受力情況與圖2中的單自由度物體類似。文中只考慮集中質量在力激勵作用下的位移的時域響應和頻域響應,不計算兩輪和帶的運動,因此,圖1中振動系統可視為單自由度系統。
以地面為參考坐標系,以集中質量的靜平衡位置為坐標原點,設集中質量的位移為x (m)且向右為正,帶的速度為vb(m/s),干摩擦為Z (t),則集中質量的運動微分方程為:

由于干摩擦的作用,使得集中質量的運動出現滑移—粘著—滑移交替出現的情況,因此分別討論滑移、粘著時的運動方程及相應的解。
其中,Z (t)表示干摩擦的大小為時間的函數,其增量形式的本構關系為:



圖4 包含雙折線模型的單自由度振動系統
3 系統響應的求解方法
由于干摩擦的作用,使得集中質量的運動出現滑移—粘著—滑移交替出現的情況,因此分別討論滑移、粘著時的運動方程及相應的解。
3.1 集中質量的運動為滑移時的運動方程
當集中質量的運動為滑移時,在用雙折線模型描述干摩擦力的情況下,干摩擦相當于剛度為ks的彈簧,因此,式(3)變為:

定義如下的變量:

則(6)變為:

式(8)為二階常系數非齊次微分方程,其解由對應的齊次微分方程的通解和非齊次微分方程的特解組成。通解只對應于振動響應的過渡階段,會隨時間推移而消失,因此不予考慮。可設式(8)的特解的形式為:

其中:
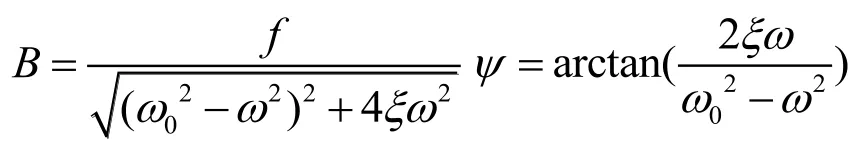
3.2 集中質量的運動為粘著時的運動方程
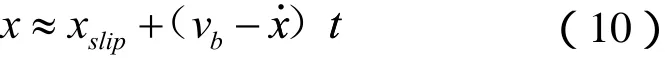
其中,xslip為當集中質量由滑移變為粘著時的臨界點所對應的位移,t為粘著段對應的時間區間的長度。
3.3滑移—粘著臨界時刻的
當滑移和粘著的運動方程分別確定后,集中質量的時域位移響應可在滑移、粘著段分段可導,因此,求解滑移—粘著—滑移變化的臨界時刻就十分重要。當集中質量的速度 時,系統由滑移變為粘著,因此可將 作為判斷臨界時刻的標準。
本文采取變步長法,求解滑移—粘著的臨界時刻,圖5為計算程序的流程圖。集中質量處于粘著的時間與處于滑移的時間之和為周期的一半,因此粘著—滑移轉變的臨界時刻可由此確定。
3.4 系統幅頻響應的求解方法
由于雙折線本構關系Z (t)為非線性的泛函,其示意圖如圖6所示,造成直接求頻響方程十分困難,因此考慮Z (t)的簡化形式。
雙折線遲滯模型的阻力具有周期性,且沒有第一類間斷點,并絕對可積,因此,可將其阻力展開成Fourier級數。
如圖7所示,可將雙折線遲滯模型的阻力分段表示:

在2處,1—2與2—3分別表示的分段函數應連續,可得:

圖5 臨界時刻計算流程圖

圖6 雙折線示意圖

xy為雙折線本構關系的滑移極限。所以,利用分段積分定理,可得阻力F的Fourier級數為:
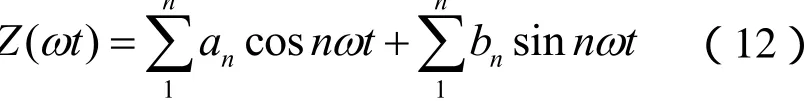
其中:
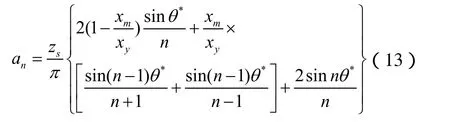

以往的文獻曾對式(12)進行頻譜分析,指出,式(12)中的高次諧波位移與基頻位移之比均低于5.5%,甚至往往低于1%。因此,可取式(13)中n=1的各項來近似代替雙折線遲滯模型的阻力。
當n=1時,簡化后可得:
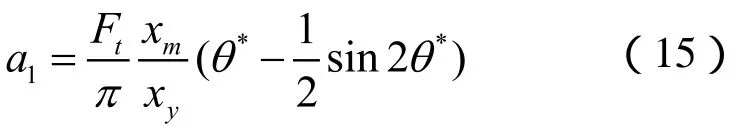

因此,雙折線遲滯模型的等效阻力為:

將式(13)代入式(1)中,再對式(1)進行傅里葉變換,經整理、簡化后最終可得:

其中,xm為集中質量位移響應的幅值,利用Newton迭代法求解非線性方程(18)即可得到集中質量的幅頻響應曲線。
4 計算結果及分析
為分析不同的系統參數對集中質量粘滑運動的影響,在幅值為20N,頻率為5HZ的簡諧激勵下,分別計算了不同參數時系統的時域位移響應。系統的各參數如表1所示。

表1 系統參數
4.1 時域響應
為分析不同的系統參數對集中質量粘滑運動的影響,在幅值為20N,頻率為5HZ的簡諧激勵下,分別計算了不同參數時系統的時域位移響應。系統的各參數如表1所示。圖7為集中質量的位移響應。由圖7可見,文中的計算方法可表征集中質量的粘滑運動,且帶速的大小對位移的幅值有影響,帶速增大時位移的幅值增大。
4.1.1 不同阻尼時集中質量的位移響應
圖8為集中質量的位移響應,由圖8可見,阻尼的大小對位移的幅值有影響,帶速增大時位移的幅值減小。

圖7 集中質量位移響應

圖8 集中質量位移響應 (m=0.5,k=10,zs=20,ks=25)

圖9 集中質量位移響應 (c=0.5,m=0.5,zs=20,ks=25)
4.1.2 不同剛度時集中質量的位移響應
由圖9可見,剛度k的大小對位移的幅值有影響,k增大時位移的幅值減小。
4.2 幅頻響應
取系統參數為 m=0.05,c=0.5,k=25,zs=20,ks=22,在幅值為30N,頻率為0~10HZ掃頻的激勵下,計算集中質量的幅頻響應,結果如圖10所示。可見當激勵頻率為5.1HZ左右時,幅頻響應達到峰值。

圖10 集中質量的幅頻響應曲線
5 結論
文中給出了干摩擦系統的建模及計算方法,分析了干摩擦系統中的參數對系統響應的影響,結果表明,文中的建模和數值方法是有效的,可供干摩擦設計借鑒。
[1] Den Hartdog,Forced vibration with combined coulomb and viscous friction[J]. Trans ASME, 1931: APM-52-15.
[2] Iwan W.F. The dynamic response of the bilinear hysteretic system [D]. Califonia: Califonia institute of technology,1961.
[3] 胡海巖, 李岳峰. 具有記憶特性的非線性減振器參數識別[J]. 振動工程學報, 1989, 2(2): 17-26.
[4] 李冬偉, 白鴻柏, 楊建春, 等. 非線性遲滯系統建模方法[J]. 機械工程學報, 2005, 41(10): 205-210.
[5] 路純紅, 白鴻柏, 胡仁喜. 金屬橡膠/橡膠復合疊層耗能器動力學模型[J]. 振動工程學報, 2008, 21(5): 493-497.

