混裝生產排產序列MILP建模與仿真優化研究

蔣國璋，肖 勇，唐秋華，王 娟，雷正奇

JIANG Guo-zhang1, XIAO Yong1, TANG Qiu-hua1, WANG Juan2, LEI Zheng-qi2

(1.武漢科技大學 機械自動化學院，武漢 430081；2.東風汽車有限公司 商用車發動機廠，十堰 442000)

0 引言

隨著現代科學技術的迅速發展，產品的生命周期已大大縮短，同時由于激烈的市場競爭及用戶對產品的個性化要求，單品種、大批量的生產已不再適應用戶對產品的多樣化需求。在新的市場環境下，企業需要尋找一種新的生產模式：多產品混裝生產。這種生產模式能夠以大規模生產的效益進行同一類型多種產品的生產，能根據用戶的需求，用大規模生產的效益完成特定產品的生產。汽車生產等以裝配生產為主的企業，多采用這種混裝生產模式。混裝線所裝配產品具有基型和多種變型產品，它們的功能和作業方式基本相同，僅僅在規格以及型號上有所區別[1]。不同產品的投產順序影響著企業的生產和整體效率提高。因此，研究混裝生產排序問題具有非常重要的意義。

1 混裝生產排序問題

1.1 問題描述

汽車混裝生產是在基本不改變現有生產手段、生產條件和生產能力的前提下，通過改變生產組織方式，在一定時間內，在同一條流水線上制造出多種不同型號、不同數量的產品[2]。在流水線上，每種規格的產品要經過每個工作站僅一次，在生產線上當多種不同規格的產品一起生產時，需要確定產品的加工順序，這樣就出現了排產問題。混裝生產線的排產問題的焦點一般都集中在投產排序問題。

1.2 解決途徑

對于混裝生產最優排序問題，其解決途徑如圖1所示。

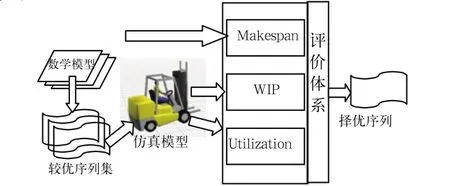
圖1 基于MILP的排產序列仿真決策體系

首先我們建立混合裝配流水線最小化makespan的數學模型，根據數學模型運算出部分較優序列，這樣得到一個較優序列集合；然后在Flexsim中建立虛擬生產車間模型，在模型source中導入每一個較優序列，驅動仿真模型運行，得到Makespan、WIP、Utilization三個目標的實際值；最后構建關于Makespan、WIP、Utilization三個目標的評價函數D(x)，對每個較優序列進行運算，將得到的D(x)的值進行比較，最大的則為最優的投產序列。

1.3 方法的異同比較

產品的排序問題是混裝生產的研究重點，Wester和Kilbridge在1963年首先對混裝生產線的排序問題進行了研究。幾十年來，很多學者對這個問題進行了大量的研究。對這些問題的研究，學者們主要是集中在目標函數的優化與排產方法的優化。本文的不同點在于對排產的優化是基于目標函數和Flexsim仿真驗證相結合的優化，并通過優化找出最優的排產序列。

2 基于MILP的混裝生產排產優化數學模型

裝配線平衡下的混合裝配線排產優化問題能夠描述為確定M個品種的D個產品在計劃期內的投產順序，優化混合裝配線的預定排產目標[4]。這里建立混合裝配流水線最小化makespan的數學模型。

1）模型參數：i：產品投產順序編號；j：工位代號；N：總裝配線上工位總數；C：流水線的節拍；n'：產品的作業元素的個數；E：作業元素的集合，。任意的記是作業元素 的直接優先元素的集合。：第m種產品的第 個作業元素的時間；所有M種產品的第 個作業元素的平均時間。

混裝流水生產線的優化模型為：

式(1)～式(3)是混裝流水線平衡優化的約束[5]，其中，式(1)保證一個作業元素分配在一個有且只有在一個工作站內；式(2)表示只有當一個作業元素的所有直接優先元素全部被分配到工作站內時，則這個作業元素才能被分配；式(3)保證分配到一個工作站內的每一個作業元素的平均作業時間不能超過給定的節拍；式(4)和(5)表示混裝生產線的排序優化約束[5]，其中，式(4)保證在排序序列的一個位置上有且僅有一個m型產品；式(5)保證在排序序列的所有位置上某一種產品的數量恰好為這種產品的需求量。

式(6)是要優化的目標函數，其計算方法如下：

每個循環開始時，第1個投產的產品在第1個工位上的開始時刻記為0，即S11=0。第個投產的產品在第個工位開始加工的時刻為：

式（7）中第i個產品在第j個工位的開始時刻為第i個產品在第(j-1)工位加工的結束時刻與第(i-1)個產品在第j個工位加工的結束時刻之間的較大值。

式(8)中第i個產品在第j個工位的結束時刻為m型中的第i個投產產品在第j個工位的加工時間與第i個產品在第j個工位的開始時刻之和。

依此類推可知：排產序列中第D'個產品在第N個工作站的開始加工時間SND和結束時刻END為：

一個排產循環中，生產制造周期為：

3 混裝排產方案評價

3.1 評價指標

1）制造周期(makespan)

制造周期(makespan)是指一個最小生產循環中，從第一個工件開始進入生產到最后一個工件加工完成所需的總時間[6]。使用不同的投產序列，makespan也會不同。對于基于時間競爭的企業來說，makespan的優化等于壓縮了供應鏈的制造周期，這樣使整個供應鏈實現快速響應，從而成為企業的新的競爭優勢來源。

2）在制品（WIP）值

在制品（WIP）是指某一時刻所有已投入生產線但尚未完成最后加工步驟的工件。對于整條生產線來說，在制品不能太多，也不能太少。太多,會導致產品的加工周期變長，使生產效率低下；太少，會使大量機器處于空閑狀態，導致資源的浪費。

3）設備利用率(utilization)

設備利用率指設備在開機狀態下用于實際加工工件的時間占開機時間的比例[6]，即：

設備利用率反映系統的忙閑程度。發動機生產設備投資龐大，運作成本高，使得投資者不愿意任何一臺設備閑置，于是不斷追求所有設備的完全利用。

3.2 評價方法

根據以上三個評價指標，運用系統工程學中功效系數法，以上評價指標對應的目標函數分別為，功效系數為di，且分別構建不同的功效函數

制造周期(makespan) 的功效函數為：

在制品（WIP）的功效函數為：

設備利用率(utilization) 的功效函數為：

其中k1,k2,k3,為權重系數，k1+k2+k3=1，取k1=0.5,k2=0.3,k3=0.2。求的幾何平均值。則評價體系函數為：

4 基于Flexsim的混裝生產系統仿真

4.1 生產環境建模

對于發動機制造車間，我們只以油漆混流生產線為例進行排產順序分析。整條油漆生產線為12臺串行處理器，運用Flexsim軟件，在實體庫中拖入相應的實體，對每個實體進行相應的設置，油漆線生產線仿真布局圖如圖2所示。

圖2 油漆線生產線仿真布局圖

4.2 制造流程仿真

仿真就是要得到有意義的仿真結果,所以要有針對性地建立與生產過程有關的模型，而對于生產過程無關或者對生產過程影響不大的設備、過程等進行簡化[7]。該汽車發動機兩種產品（D、H）的總成裝配生產線流程分別為：

3/4裝配→油漆→1/4裝配→測試→環境

3/4裝配→1/4裝配→測試→油漆→環境

4.3 制造過程控制仿真

針對不同的方案，設置模型中的對象參數，其中source 1表示上游生產線運送到下游的半成品發生器，source每隔7.5min投放一產品，對其進行不同方案的投產序列設置。然后對不同類型的產品賦予不同的顏色，On Exit 程序設置如下：

在整條油漆生產線中，每個處理器對產品D的處理時間設置為7.5min，對產品H的處理時間設置為6min。程序設置如下：

5 仿真實例與分析

為了降低在制品數和生產線緩存，需要優化不同品種產品的排產順序。以其油漆混流生產線為例，其生產線需要生產D、H兩種型號的發動機。需要構造全部可行排產序列，尋找最優的作業方案。

某日需求量為：D型60臺、H型45臺。采用循環排序法，將需求集{60，45}各個元素除以最大公約數15得到一個集合{4，3}即為最小比例集。在排產操作中，只需對最小比例集{4，3)中的共7個產品排序。通過已建立的最小化Makespan的數學模型，得出如下4種可能的最優投產排序方案：方案1：D-D-D-D-H-H-H;方案2：D-H-H-D-DH-D;方案3：D-D-H-D-H-D-H;方案4：H-H-D-D-HD-D。

在實際投入生產之前，用Flexsim軟件對4種投產順序進行仿真。參數設置完成后，先編譯，驗證無誤后仿真運行。以方案1:D-D-D-D-H-H-H為例，其中紅色代表產品D，綠色代表產品H,模型運行效果如圖3所示。

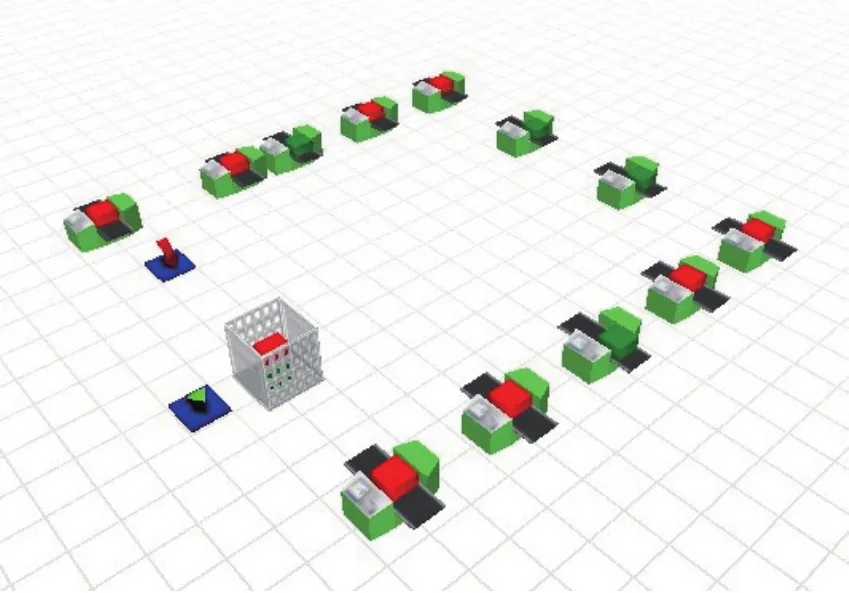
圖3 油漆生產線運行效果圖

對4種不同的投產方案進行模型運行后，對數據進行統計。隨機選取處理器8，對4種不同的方案進行運行后，運行時間設置為300min，比較制造周期的大小，生產線的緩存大小和處理器8的工作效率。運行數據如表1所示。

表1 方案運行數據

以方案1為例，制造周期(makespan)的功效函數為：

在制品（WIP）的功效函數為：

設備利用率(utilization) 的功效函數為：

比較以上4種方案，可知D1為最大值，故方案1為最優方案。

6 結束語

汽車發動機制造車間生產排序是一個非常復雜的離散動態事件。采用建立虛擬生產車間模型進行仿真的方法能夠節省車間調度的驗證成本，并且能夠很大程度上反映生產車間的實際情況。

針對發動機車間的調度問題，首先通過建立MILP數學模型，得出可能的最優排產方案，然后使用Flexsim軟件建立虛擬生產環境，對不同品種產品的投產序列進行仿真驗證。對得出的實驗結果進行分析，建立評價函數，比較計算結果，從而能夠找出最優的排產方案。說明利用MILP數學建模與Flexsim建模相結合的優化方法，能夠為企業生產線排產提供理論依據。

[1]唐秋華,席忠民,陳平和,嚴運兵.混裝線投產序列和工位任務的協同調度機理[J].工業工程,2008,11(1):20-24.

[2]劉飛.CIMS制造自動化[M].北京:機械工業出版社,l997.

[3]Stefan Voβ,Andreas Witt.Hybrid flow shop scheduling as a multi-mode multi-project scheduling problem with batching requirements:A real-world application[J].Int.J.Production Economics,2007,105:445-458.

[4]Kim Y K,Hyun C J,Kim Y.Sequencing in mixed model assembly lines:A genetic algorithm approach[J].Computers＆Operation Research,1996,23(12):1131-1145.

[5]宋華明,馬士華.混合裝配流水線上最小makespan的協同優化[J].系統工程理論與實踐,2007,27(2):154-160.

[6]喬非,許瀟紅,方明,吳啟迪.半導體晶圓生產線調度的性能指標體系研究[J].同濟大學學報,2007,35(4):538-542.

[7]趙建輝,王紅軍.基于Flexsim的混流裝配線投產順序的仿真[J].微計算機息,2007,23(24):29-31.