混合智能算法在需水預測模型中的應用

王 哲，楊學軍，柳 林

（海河水利委員會水文局，天津 300170）

傳統需水預測方法適用于單一幾何增長平穩的序列，并不能反映需水預測中各影響因素之間的動態相互制約關系。20世紀90年代至今，許多學者開始研究支持向量機、人工神經網絡等基于數據挖掘、運用計算機智能技術的新方法，這些方法的良好預測性能得到了廣泛關注[1]。針對支持向量機模型（Support Vector Machine，簡稱 SVM）在需水預測中一些關鍵參數如不敏感損失參數、核參數及懲罰系數等難以確定的問題，提出了運用混合智能算法優化SVM的參數，建立基于混合智能算法的需水預測模型，以減少參數選擇的盲目性，提高SVM的預測精度。

1 基于混合智能算法的需水預測模型

1.1 支持向量機

支持向量機通過非線性映射將輸入向量從原空間映射到高維空間，在高維空間進行線性回歸[2]；同時運用結構風險最小化原則并利用原空間的核函數取代高維空間的點積運算，使復雜的計算得以簡化。

最小二乘支持向量機（LS-SVM）將不等式約束替換為等式約束，且將誤差平方和損失函數作為訓練集的經驗損失，簡化了計算復雜性，求解速度相對加快[3]。

LS-SVM的核函數包括徑向基函數（RBF）、多項式函數、Sigmoid函數等。由于徑向基核函數的泛化能力比較強，因此采用徑向基核函數，其形式如下：

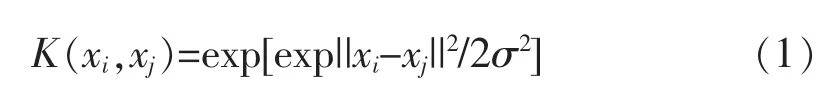
LS-SVM需要確定核參數（σ）和懲罰系數（c），而上述參數的確定缺乏有效參考依據和規則，盲目選擇參數降低了模型的預測精度。

1.2 混合智能算法的基本思想

粒子群算法（PSO）有記憶功能，所有粒子都會被保存，而遺傳算法（GA）在尋到最優解的同時以前的粒子隨著種群的改變而被破壞。PSO是一種單項信息共享機制，僅通過當前搜索到最優點進行信息共享；而GA則在整個種群染色體之間互相共享信息，整個種群較均勻地向最優域移動[4]。因此，基于遺傳和粒子群的混合智能算法將粒子群算法與遺傳算法相融合，汲取2種算法的優點，克服各自的缺陷，以使其在時間效率上優于遺傳算法，在求精確解效率上優于粒子群算法。

混合智能算法的基本思想是利用粒子群算法并行性、記憶能力以及良好的全局尋優能力，避免搜索陷入局部最優，同時借鑒遺傳算法中的進化思想，利用雜交、變異算子來進行局部尋優，使其能快速搜索到全局最優點。在搜索解的過程中通過雜交操作加強了對粒子間區域的搜索能力以利用現有而未能合理利用的信息產生更好的解；引入變異操作產生新的解以增加種群的多樣性從而減少陷入局部最優的可能性，避免進化過程在早期就陷入局部解而進入終止過程，使之在盡可能大的空間中獲得質量較高的優化解。

1.3 基于混合智能算法的LS-SVM參數選取

在LS-SVM求解中，懲罰系數 、核函數及其參數的選擇對模型的學習精度和泛化能力的好壞起著決定性作用[5]。

（1）選擇核函數：研究和實驗表明，RBF是比較好的選擇。本文亦采用RBF作為核函數。

（2）懲罰系數（c）：c值較大則允許的誤差較小，c值較小則允許較大的誤差，c值過大或過小都會使系統的泛化性能變差。一般選擇c?[0.1 50 000]。

（3）核參數（σ）：控制最終解的復雜性。樣本輸入范圍廣，σ取值大；反之，則σ取值小。σ取值太大或太小亦會使系統的泛化性能變差。一般選擇σ?[0.01 100]。

參數c、σ，特別是它們之間的相互影響關系對LS-SVM模型的復雜度、泛化性影響很大[6]。在參數選擇時除了對單個參數進行優化還應綜合考慮這2個參數形成的參數對，這樣逐一的選取方法既費時也不科學。而且選取出的較優解，雖然花費了很多時間，得到的結果也不一定是最優的。為此，筆者采用混合智能算法實現對LS-SVM模型的核參數（σ）和懲罰系數（c）聯合優選。

在優選過程中雖然可以任意指定參數訓練LSSVM計算訓練誤差，以此時訓練誤差為適應值，但是這樣容易使模型過度擬合而削弱了模型的泛化能力。最典型的解決方法為使用交互驗證技術（Crossvalidation）。適應度函數為求取訓練數據集交叉驗證MAPE（Mean Absolute Percent Error）的最小值，即：

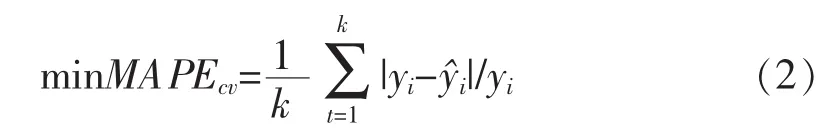
式中：k為總訓練樣本子集數，一般取k=5或10；yi為第i個實際值向量；y?i為預測值向量。

筆者提出的基于混合智能優化算法的需水預測模型，即以最小化訓練數據集的交叉驗證誤差為基礎，搜尋最佳化的SVM回歸參數值，以期能避開產生過度擬合的風險，提高LS-SVM預測模型的準確度。

1.4 基于混合智能算法的LS-SVM需水預測模型

根據社會經濟需水影響因素的分析，可知影響需水量的因素有很多，如人口、經濟發展水平、居民生活水平、水價、節水水平、產業結構等。這些因素有一些是不確定的，有一些是隨時間變化的。設需水量為因變量，影響因素為自變量，則以下式作為描述需水量預測的數學模型，即：

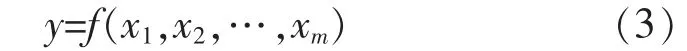
式中：y 為需水量；x1，x2，…，xm代表的是影響需水量因素。

影響需水量的因素繁多且需水用水影響因素之間關系復雜，因此采用LS-SVM來擬合式（3）。需水量的預測問題轉化為由m個影響變量和1個輸出量的回歸問題?；诨旌现悄芩惴▋灮疞S-SVM的需水量預測建模步驟如下：

（1）確定需水量影響因素。將需水量影響因素輸入模型，需水量為模型的輸出量[7]。將觀測數據分成兩部分，一部分數據作為訓練樣本進行參數估計，剩余數據用于預測檢驗，記輸入矢量為X，則：

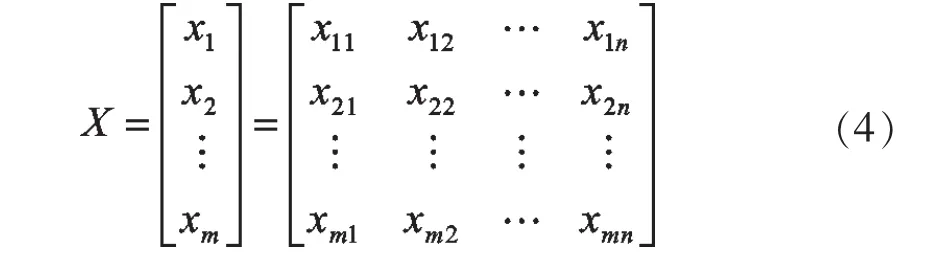
式中：m為影響需水量的主要因素個數。模型輸出為需水量數據 Y=[yi]1×n。

（2）將輸入變量、輸出變量進行歸一化處理。（3）對模型參數c和σ進行優選。

步驟1：初始化。每個粒子由2維參數組成（c，σ），設置群體規模（N）、最大迭代次數（itermax），隨機給出初始粒子和粒子初始速度，設定學習因子（c1和c2），給定算法的最大、最小慣性權值因子 （wmax和wmin），變異概率（p0），行為選擇概率（p1），模式搜索步長（bc）及誤差（eps）。

步驟2：評價種群。以適應度值評價粒子的優劣，粒子的適應度函數值越小，則粒子性能越好[8]。采用粒子個體對應的c和σ，建立支持向量機的學習預測模型，按式（1）計算每個個體的適應值。

步驟3：更新每個粒子的位置和速度。根據行為選擇概率（p1），進行交叉操作和模式搜索，并且考慮更新后的速度和位置是否在限定的范圍內。

步驟4：判斷進化是否停滯。若是，則按變異概率（p0）對粒子群中的粒子進行重新初始化；否則，轉入下步。

步驟5：檢查結束條件。若比較次數或者精度值滿足預設精度，算法收斂，最后1次迭代的最優值即為所求最優值，尋優結束；否則t=t+1，轉至步驟2，算法繼續迭代。

（4）將最優參數向量（c、σ）賦予 LS-SVM，用樣本數據對LS-SVM模型進行訓練，得到2個支持向量（a和b）的值。進而預測樣本進行預測，通過與實測需水量進行比較，進行模型校驗。

（5）最后，用該支持向量機回歸模型進行需水量預測。

2 實例研究

將基于混合智能算法優化LS-SVM的需水預測模型運用于秦皇島市第二產業需水預測過程中，選取與用水量相關性較好、又能衡量需水情況的因子：工業產值、工業規模以上產值、工業規模以下產值、火核電產值、工業水重復利用率、建筑業產值、水價，以2000—2005年調查數據為基礎建立基于混合智能算法的支持向量機預測模型，預測2006、2007年秦皇島市第二產業需水量。

利用模型針對上述學習樣本進行秦皇島市第二產業需水量預測。能否合理確定LS-SVM的懲罰系數（c）和核參數（σ）直接影響到模型的精度和推廣能力，筆者通過混合智能算法優化LS-SVM參數對（c，σ）。取群體規模為60，最大進化次數為200，粒子的向量維數為2，PSO加速常數c1=c2=1.5，慣性權重（ω）由 0.9 線性變化到 0.4，選擇概率（P1）為0.5，變異概率（P0）為 0.1。 模型計算參數結果，見表1。

通過對參數的搜索，第87代出現了最佳適應值，其值為MAPE=3.669 5。因此，把第87代的最佳個體作為最佳化參數值，此時的參數值分別為c=963、σ=0.274 1，將此參數組合帶入預測模型中，對秦皇島市2006—2007年第二產業用水進行預測。

表1 模型計算參數結果

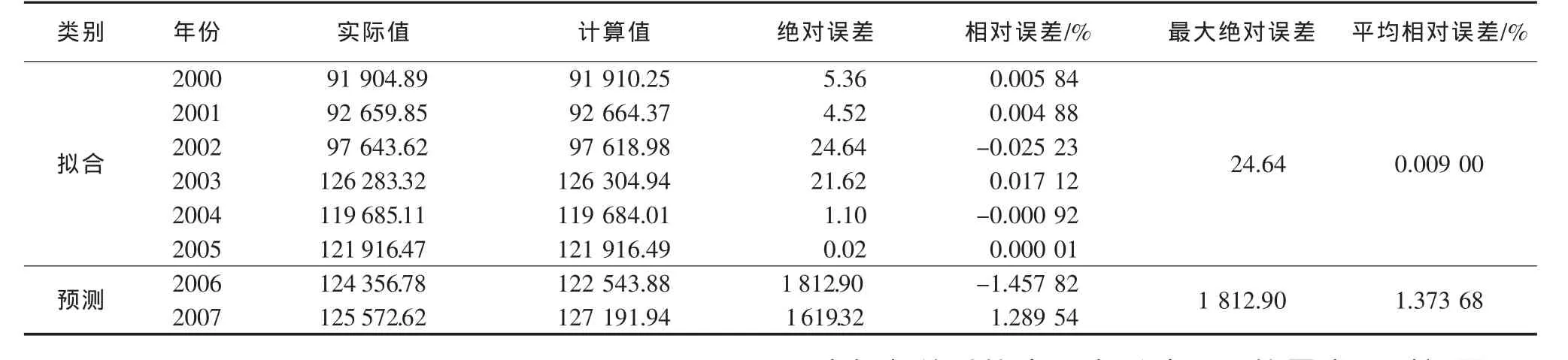
表2 實際值與預測值對比

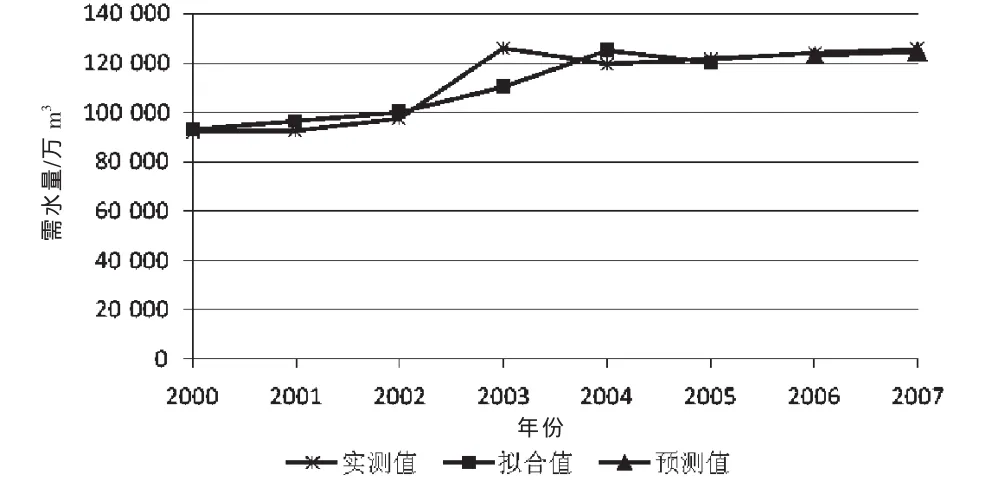
圖1 模型實際值、擬合值與預測值對比

由表2和圖1可以看出，模型計算的擬合值和預測值與秦皇島市的第二產業實際用水吻合較好。通過統計分析，2000—2005年的擬合部分最大相對誤差為0.025 23%，平均相對誤差為0.009%；2006—2007年的預測部分，最大相對誤差為1.457 82%，平均相對誤差為1.373 68%，均小于5%。由此可見，利用該模型預測秦皇島市第二產業需水發展的結果是令人滿意的，具有較高預測精度。

3 結語

（1）基于混合智能算法優化LS-SVM的需水預測模型能夠快速地尋優，該方法較單一智能算法具有一定的優越性。

（2）研究實例表明，筆者建立的優化模型能夠解決復雜關系的多因素影響因子的需水預測問題，預測模型擬合精度較高，預測結果較合理。

（3）針對預測結果存在誤差的問題，在今后的運用過程中需加大樣本容量，以便提高預測的準確性。

[1]劉衛林.幾種需水量預測模型的比較研究 [J].人民長江，2011，42（13）：19-22.

[2]張偉，吳丹，李小奇，等.基于最小二乘支持向量機的大壩應力預測模型[J].水利與建筑工程學報，2011（1）：26-29.

[3]熊偉麗，徐保國.基于PSO的SVR參數優化選擇方法研究 [J].系統仿真學報，2006（9）：22-26.

[4]曹成濤，徐建閩 .基于PSO-SVM的短期交通流預測方法[J].計算機工程與應用，2007（15）：15-18.

[5]梅松，程偉平，劉國華.基于支持向量機的洪水預報模型初探[J].中國農村水利水電， 2005（3）：34-36.

[6]Yu X Y，Liong S Y，Babovic V.EC-SVM approach for realtime hydrologic forecasting[J].Journal of Hydroinformatics，2004，6（3）：209-223.

[7]陳磊，張土喬.基于最小二乘支持向量機的時用水量預測模型[J].哈爾濱工業大學學報（自然科學版），2006，38（9）：1528-1530.

[8]鐘偉，董增川，李琪.混合算法優化投影尋蹤模型的需水預測研究[J].水電能源科學，2010，28（7）：31-33.