破圈法應用中的誤區分析

閆超君

(安徽水利水電職業技術學院，安徽合肥231603)

工程實踐中，常用雙代號網絡圖表達工作之間的相互關系和整個工程任務的全貌，通過分析計算，找出對全局有決定性影響的關鍵線路和各項關鍵工作，據此對任務作出切實可行的全面規劃和安排。確定雙代號網絡圖關鍵線路的方法有很多，諸如:直接法、總時差最小法、節點參數法、時標網絡圖法、標號法、破圈法。其中破圈法運用時不需大量計算，是一種比較簡便直觀的方法，但由于在運用破圈法時，有一些誤區存在。為此，在實際工作中很少有人運用，使得破圈法應用不是很廣泛。

1 對破圈法的初步認識

在雙代號網絡圖中有許多節點和箭線，這些節點和箭線形成了許多封閉的“圈”，這些“圈”是指在兩個節點之間由兩條線路連通該二個節點所形成的最小圈。破圈法是將網絡中各個封閉圈的二條線路按各自所含工作的持續時間來進行比較，破掉持續時間短的線路，逐個“破圈”，直至圓圈不可破時為止，最后剩下的線路即為網絡圖的關鍵線路如圖1。

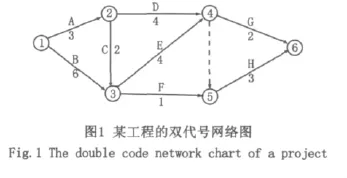
從節點①開始，節點①、②、③形成了第一個圈，從節點①到節點③有二條線路，一條是①→③，一條是①→②→③。①→③需要時間是6，①→②→③需要時間是5，因6﹥5所以切斷①→②→③。

從節點②開始，節點②、③、④形成了第二個圈，從節點②到節點④有二條線路，一條是②→③→④，一條是②→④。②→③→④需要時間是6，②→④需要時間是4，因6﹥4所以切斷②→④。

從節點③開始，節點③、④、⑤形成了第三個圈，從節點③到節點⑤有二條線路，一條是③→④→⑤，一條是③→⑤。③→④→⑤需要時間是4，③→⑤需要時間是1，因4﹥1所以切斷③→⑤。

從節點④開始，節點④、⑤、⑥形成了第四個圈，從節點④到節點⑥有二條線路，一條是④→⑤→⑥，一條是⑤→⑥。④→⑤→⑥需要時間是3，④→⑥需要時間是2，因3﹥2所以切斷④→⑥。剩下的即為關鍵線路，見圖2所示中的雙箭線。

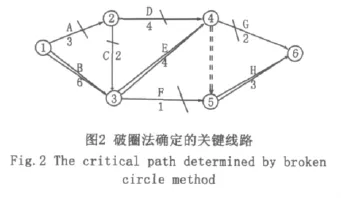
2 誤區分析

上述示例看似正確，但有不少誤區存在。比如按上述方法確定圖3所示的雙代號網絡圖，關鍵線路就確定不出來，甚至判斷出錯誤的關鍵線路。

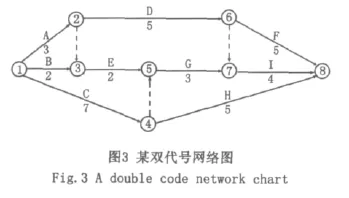
按上述所述破圈法，從節點①開始，節點①、②、③形成了第一個圈，從節點①到節點③有二條線路，一條是①→③，一條是①→②→③。①→③需要時間是2，①→②→③需要時間是3，因3﹥2所以切斷①→③。

從節點①開始，節點①、③、④、⑤形成了第二個圈，從節點①到節點⑤有二條線路，一條是①→③→⑤，一條是①→④→⑤。①→③→⑤需要時間是4，①→④→⑤需要時間是7，因7﹥4所以切斷①→③→⑤。

同理可切斷⑦→⑧，④→⑧。關鍵線路如圖4雙箭線所示。但是，用此方法判斷出的關鍵線路是錯誤的。正確的關鍵線路如圖5雙箭線所示。

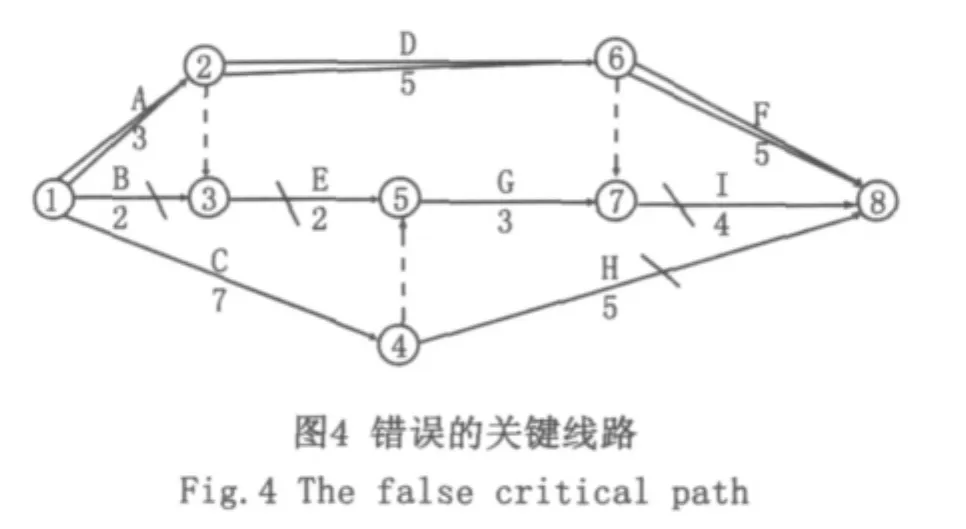
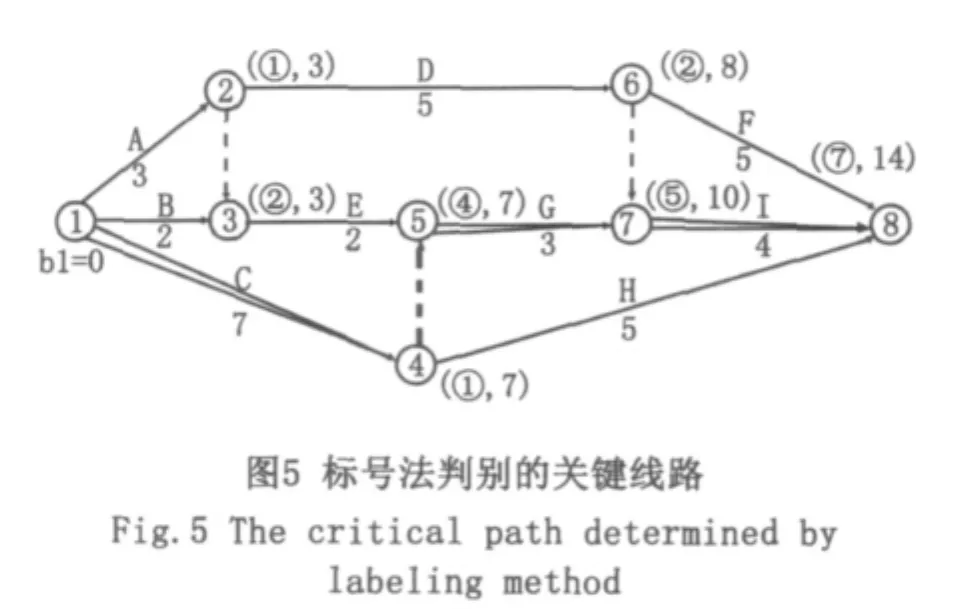
出現破圈法判別的關鍵線路不正確的原因就是大家對破圈法的錯誤理解，判斷中存在誤區，現分析一下存在的誤區。

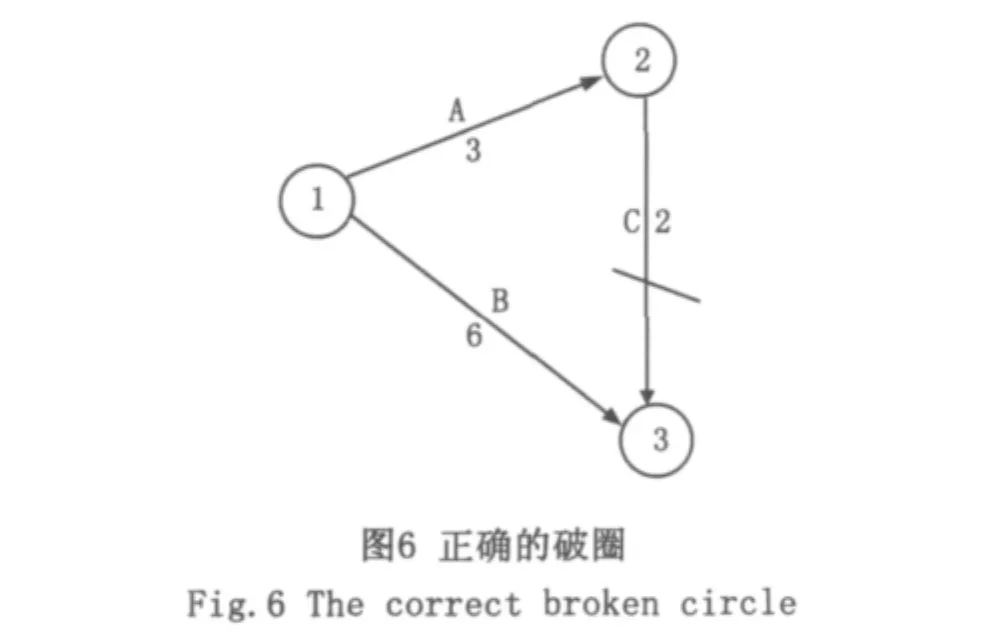
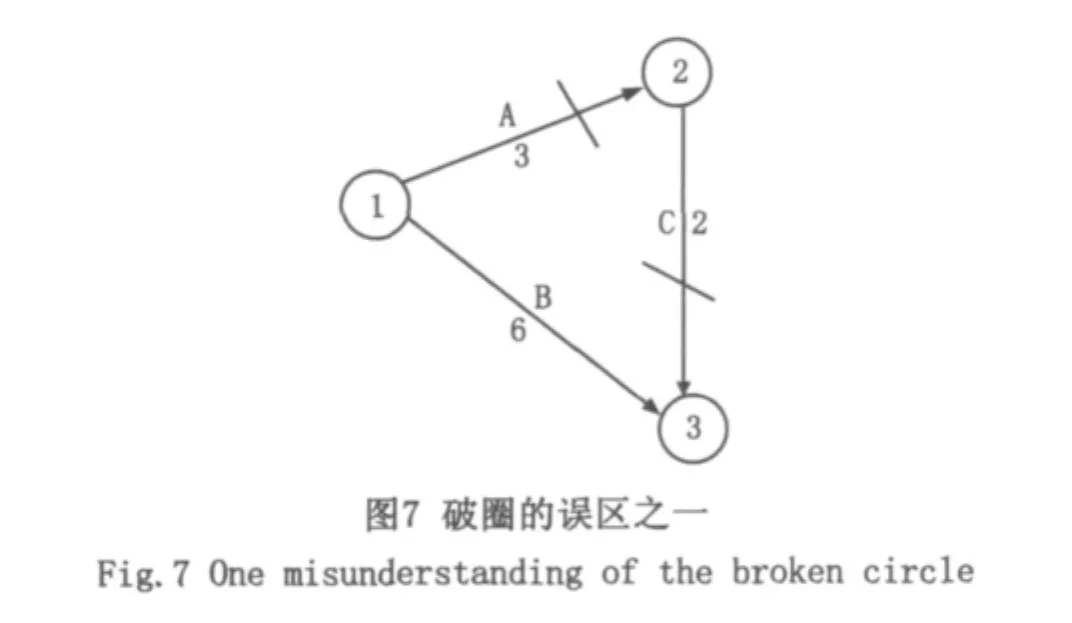
誤區一:破圈時，去掉一整條線路。凡遇到節點有兩個及兩個以上的內向箭線時，肯定有一個圈，比較時間長短，把時間較短線路流進的一個箭線去掉，如圖6所示只去掉②→③，誤區是把整條線路去掉如圖7所示，去掉了①→②箭線和①→③箭線。

誤區二:破掉的箭線，找下一個圈時還在用。破圈法找圈時，破掉的箭線不能再次用，誤區是去掉的箭線還繼續用。圖4中到⑤節點有兩個內向箭線，一定有個最小的圈，此最小的圈不是由①→③→⑤和①→④→⑤兩條線組成的圈，因為①→③已破掉，而是由①→②→③→⑤和①→④→⑤兩條線組成的圈。圖4中到⑦節點有兩個內向箭線，一定有個最小的圈，此最小的圈不是由②→③→⑤→⑦和②→⑥→⑦兩條線組成的圈，因為③→⑤已破掉，而是由①→②→⑥→⑦和①→④→⑤→⑦兩條線組成的圈。

誤區三:破圈法不能判別所有雙代號網絡圖的關鍵線路。由于不能正確地找到“圈”，就不能正確地破“圈”，以至于雙代號網絡圖利用破圈法確定關鍵線路，破到最后，連一條完整的線路都沒有，就不能確定出關鍵線路，于是認為，破圈法不科學，不好用，不能判別所有雙代號網絡圖的關鍵線路。正是因為此原因，很多教科書上都不介紹破圈法。實際是所有的雙代號網絡圖都可以用破圈法判別出關鍵線路。

3 正確利用破圈法確定關鍵線路

通過對破圈法的再認識，走出誤區，正確判別雙代號網絡圖的關鍵線路。對圖3所示網絡圖進行破圈法判別關鍵線路。

從節點①開始，到③有兩條內向箭線，節點①、②、③形成一個圈，即從節點①到節點③有二條線路，一條是①→③，一條是①→②→③。①→③需要時間是2，①→②→③需要時間是3，因3﹥2所以切斷①→③。

到節點⑤有兩條內向箭線，但①→③箭線已被斷開，所以節點①、③、④、⑤不能形成一個圈，應擴大范圍找“圈”，節點①、②、③、④、⑤形成一個圈，即從節點①到節點⑤有二條線路，一條是①→②→③→⑤，一條是①→④→⑤。①→②→③→⑤需要時間是5，①→④→⑤需要時間是7，因7﹥5所以切斷③→⑤。

到節點⑦有兩條內向箭線，由于③→⑤已破掉，所以節點②、③、⑤、⑥、⑦不能形成一個圈，應擴大范圍找“圈”，節點①、②、④、⑤、⑥、⑦形成一個圈，即從節點①到節點⑦有二條線路，一條是①→②→⑥→⑦，一條是①→④→⑤→⑦。①→②→⑥→⑦需要時間是8，①→④→⑤→⑦需要時間是10，因10﹥8，所以切斷⑥→⑦。

到節點⑧有三條內向箭線，一定有兩個圈，節點④、⑤、⑦、⑧形成一個圈，即從節點④到節點⑧有二條線路，一條是④→⑤→⑦→⑧，一條是④→⑧。④→⑤→⑦→⑧需要時間是7，④→⑧需要時間是5，因7﹥5，所以切斷④→⑧。由于⑥→⑦已破掉，節點⑥、⑦、⑧不能形成一個圈，應擴大范圍找“圈”，節點①、②、⑥、⑧、④、⑤、⑦形成一個圈，即由①→②→⑥→⑧，和①→④→⑤→⑦→⑧這兩條線形成另一個圈，①→②→⑥→⑧需要時間是13，①→④→⑤→⑦→⑧需要時間是14，因14﹥13，所以切斷⑥→⑧，如圖8所示。

剩下的線路，能從起點走到終點的線路就是關鍵線路，①→②→⑥走不通，不是關鍵線路，①→④→⑤→⑦→⑧從起點走到了終點，故是關鍵線路，如圖8雙箭線所示。

從圖8可以看出，關鍵線路與標號法確定的關鍵線路(圖5)一致。

4 結束語

通過對破圈法的誤區分析，運用破圈法時注意三原則:破最小的圈、破過的線)不可以再用、只破流進箭線的一個箭線。走出誤區，就能快速地運用破圈法判別雙代號網絡圖的關鍵線路，而且所有的雙代號網絡圖都可以用破圈法確定關鍵線路。

破圈法不需計算時間參數，通過破圈就可以確定出關鍵線路，簡單直觀，是一種非常實用的確定雙代號網絡圖關鍵線路的方法。

［1] 閆超君.建設工程進度控制［M] .合肥:合肥工業大學出版社，2009.

［2] 龐素珍.用圖論理論正確掌握破圈法［J] .河北北方學院學報，2007(5):80－82.

［3] 董躍華，李云浩.用破圈法實現普利姆算法［J] .江西理工大學學報，2008(4):20－21.

［4] 郭月明.運籌學［M] .廣州:華南理工大學出版社，2001.

［5] 李濟民.用圖論指導破圈法的學習［J] .經濟與管理，1998(1):42－43.

［6] 周 迎.破圈法解動態規劃中的最短路問題［J] .西昌農業高等專科學校學報，2003(3):68－69.