基于圖割的圖像分割綜述

辛月蘭

0 引言

近年來，圖割技術作為一種魯棒的能量最小化方法，得到越來越多的重視，通過對圖像分割的推廣，圖割技術已經應用在整個計算機視覺領域。

1 圖割基本理論

1.1 圖割基本理論的概述

設一個無向圖為G = 〈V，E〉，V 為圖中節點的集合，E 為連接節點的邊集。通常，節點代表了像素、體元或其它特征，而圖中也包含一些附加的特殊節點，稱為終端節點。在立體視覺應用的能量最小化方法中，圖的結構有很多種形式，但大多數都是基于規則的二維或三維網格圖。

一個具有兩個終端節點的二維圖，定義V = { s，t} ∪P為無向圖 G 中的節點，包含了兩個表示“目標”和“背景”標簽的特定終端節點，分別為源點s 和匯點t，以及一系列非終端節點的集合P。圖中每一邊被賦與一個非負的容量( 或稱權值) ，邊緣代價通過邊緣厚度（線的粗細）表現出來。圖中的邊可以被分為兩類: n-links 和t-links。連接非終端節點的邊稱為n-links; 連接像素到終端節點的邊稱為t-links。

Boykov[1,2]的交互式分割的具體過程，如圖1所示：

圖1 二維圖網絡（基于圖割理論進行圖像分割）

1.2 分割能量

其中公式（2）

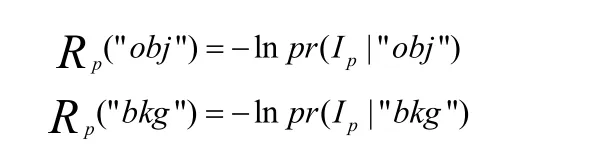
這里負對數是通過MAP-MRF構想產生的公式（3）

B(A)項包含分割A的邊界性能，系數Bp,q≥0應該看作p和q之間不連續的一個處罰，

如圖 1（a）所示，“O”為交互設置的目標種子點，“B”為交互設置的背景種子點；圖1（b）是根據（1）式建立的能量函數所構造的網絡圖，網絡圖的權值，如表1所示：

表1 邊權值定義

圖1（c）是使用最大流/最小割算法對圖1（b）建立的網絡圖進行的切割；圖 1（d）是根據圖割獲得的圖像分割結果，相當于二元分區將圖像劃分為“目標”和“背景”部分。

1.3 圖割的能量最小化

根據能量優化的觀點求解最小圖割，是目前圖割中的主要求解方法。該方法需要根據圖像的特征信息，建立合適的能量函數，然后根據能量函數，建立圖論中的網絡圖，通過對網絡圖采用最大流/最小割算法，獲得分割的結果。

從理論上講，基于圖割的能量函數最小化方法，可以提供能量函數的全局最小化；也就是說，即使產生的結果是局部最小值，也是具有很強性質的局部最小值。因此對特定領域里一些有爭議的問題，可利用基于圖割的能量最小化方法，得到最準確的解決方式，因此，將其應用到圖像分割上，以期得到更好的分割結果。

計算機視覺中的很多相關問題，都可以歸結為能量最小化的問題[3]。能量最小化存在很多優點：首先，它可以與解決它的算法分開，清楚地描述需要解決的問題；其次，它可以用空間光滑的結果來求解多義性的問題；最后，能量最小化避免了陷入早期硬約束的窘境。

能量最小化在計算機視覺中，已經存在很長的一段歷史，并廣泛應用于很多問題中，如光流、圖像恢復、表面重構、紋理合成以及邊緣檢測等。梯度下降和模擬退火算法，是兩種典型的能量最小化方法，前者適用于所有連續變量的函數，而后者幾乎可以用于所有的離散變量函數。但這些方法可能會產生比較差的結果，因為它們經常陷于局部最小化中，或者是花費很長時間才能收斂。在實踐中，即使在非常簡單的二值圖像修復中，模擬退火得到的解，離全局最小也很遠。

1989年，Greig等人[3]將圖割理論引入計算機視覺領域，出現了基于圖割的能量最小化方法，它克服了以上兩者的不足，實現了能量的全局最優化。它將圖像分割問題轉換為圖論中網絡圖的切割問題，依據最小割準則，使切割后劃分的區域間具有最小的相似性。基于圖割的圖像分割，將圖像分割問題轉換為能量函數的優化問題，通過合適的能量函數建立相應的網絡圖，通過最大流/最小割算法求解網絡圖最小割，從而獲取圖像分割的結果。

2 圖割的研究現狀

2.1 圖割的發展狀況

近年來，基于圖割的能量最小化方法在圖像處理和計算機視覺中的應用越來越廣泛。圖割理論自1989年首次被發現，可以最小化計算機視覺中的某個能量函數，且只限于二值圖像。1998年Roy和Cox首次用來解決非二值圖像問題，其方法是圖的最大流/最小割算法。Yuri Boykov和Maric-Pierre Jolly[4]2001年首次將圖割（graph cuts）理論引入計算機視覺領域，他們提出并實踐了一種新的基于能量最小化進行目標分割的方法，并提出了利用最大流/最小割算法，進行全局組合優化的目標提取方法。自此以后，利用圖割來解決計算機視覺的問題越來越受到歡迎。許多研究者提出了多種分割算法，如 Rother[5]等人，在 2004年提出的GrabCut算法，是目前目標提取效果較好的方法；Ning Xu[6]等人提出的基于圖割理論的活動輪廓（GCBAC）算法，克服了傳統的活動輪廓算法容易陷入局部最優的缺陷，能夠快速、準確地收斂到目標的邊界。

國內自2006年有論文發表以來，用圖割研究的領域也越來越廣。電子科技大學、安徽大學和吉林大學在圖像復原、圖像匹配、三維重構和目標提取、圖像去噪、運動目標檢測、合成、分割等多個領域都有研究。

為得到更加魯棒的分割性能，許多學者試圖將形狀先驗引入到圖割分割過程中。這種將高層先驗引入到底層分割的做法是近年來的新趨勢。文獻［7］用一個初始輪廓在終端邊緣和執行圖割迭代開始加強了形狀先驗模型，給出一組訓練的形狀，他們的方法是利用核主成分分析（kPCA），建立一個統計形狀空間，在每一步迭代，這個形狀空間標記的上一個圖用來作為先驗概率圖，負記錄被分配到終端權重。雖然這方法取得了可喜成果，但他們的外形產生的能量不是基于形狀的度量標準，此外，該方法不能同時處理形狀的仿射變換和同時分割多目標物體。文獻［8］提出了一個新的廣義形狀先驗，稱為星型先驗。它可以表示比緊湊先驗更為一般的形狀，而且同樣只需提供一個內部點就滿足分割需要。特別是對于凸形狀，這個點可以選在內部任意位置而不會對最終分割結果產生影響。但文獻中星型先驗的計算方法略顯復雜，需要計算圖像中內部點的所有離散直線。Lang 等人［9］對其提出了改進，在簡化計算步驟的同時，保證了與原算法分割效果的一致性，而且，可以處理目標具有復雜紋理的情況。

圖割理論在國外的計算機視覺領域中，得到了成功且廣泛應用，但在國內的研究還處于初級階段，尤其是圖割理論用于圖像分割這一領域的研究報道并不多，將圖像的形狀等先驗知識引入圖割技術的研究更是寥寥無幾，因此，基于圖割理論的圖像分割在現階段仍然是一個研究熱點。

2.2 圖割的應用

圖割技術因其能量全局最優化而格外引人注目，是計算機視覺中正在興起的一個有用的工具。

目前，通過各種方法將形狀先驗融入到圖割技術中是圖割研究的熱點之一。 例如文獻[23]的作者提出一種全新的方法分割一個特殊類的形狀，調整光滑項防止過大，如果違反這個規則用一個緊湊形狀來維護，然而，在實際應用中涉及到變化的形狀時該方法是受限的。文獻[24]的作者提出了一種分割時執行迭代的類似方法，每步迭代擬合一個橢圓到當前分割，定義為形狀先驗聯合分割內部，然而，如緊湊的方法。該方法也不能推廣到高度可變的形狀，同時，這種方法合并形狀先驗作為一個附加的固定權重，不是概率意義上的貝葉斯先驗。為獲取更多的任意形狀，文獻[25]作者在光滑項中使用一個距離函數幫助邊界定位，執行圖割前決定形狀分割和固定對準，該方法似乎對初始估計相當敏感，還有，因為形狀先驗在邊界項的作用，在某種意義上有一個局部效應和對錯位的敏感。

2004年，Boykov和Kolmogorov在增廣路算法基礎上，提出了一種新算法[11]求解最大流，并將其應用于圖像分割及計算機視覺中，大幅度地提高了求解速度。在 push-relabel算法基礎上，Hochbaum[12,13]提出采用pseudoflow解決最大流問題，在Olivier Juan和Yuri Boykov提出的Active Graph cuts[14]圖割方法中，應用此最大流算法對網絡能量函數進行了求解；文獻[15]提出了一種基于簡化網格圖的立體匹配算法.算法通過區域匹配，得到每個像素的初始視差值，然后只保留完整網格圖的部分可能的視差值，去除其余大部分的節點和邊緣，建立簡化的網格圖.該方法大為縮減了網格圖的容量，縮短匹配所用時間，并且能夠選用更大的視差范圍.

Boykov[1]等人在2000年發表了一篇在N維空間交互式的圖像分割方法，以其簡潔的交互方式、較快的處理速度以及能將各種信息融合，而引起人們的關注；Rother[16]等在Boykov等人的基礎上提出Grab cut算法，通過高斯混合建模與數據的估計代替 Boykov的直方圖模型，可對彩色圖像進行分割，而且使得交互更為方便，目前是交互式圖像分割中最好的一種方法；文獻[17]提出一種新的基于圖割(graph cuts)的交互式圖像分割方法。該方法將圖像的紋理、色彩、邊緣等多種特征，通過一個概率模型結合在一起，其中紋理和色彩用以Texton 為基的直方圖來建模，并用Fisher 判別準則來對特征空間進行降維。利用圖割方法，可以快速求解該模型下的最優分割；文獻[18]針對腹部CT 圖像中組織分割的問題，提出了一種基于圖割與改進的快速水平集的交互式分割方法；文獻[19]提出一種基于圖割的全變差( TV) 圖像去噪算法， 該算法將全變差去噪模型的能量函數最小化問題轉化為圖的最小割問題, 然后采用圖割技術( 最大流/最小割算法) 求得能量函數的全局最優解。

文獻[20]基于多尺度思想對圖像分割，它先對原始圖像下采樣，用圖割對低分辨率圖像分割，然后將分割的結果映射到較高分辨率圖像的帶狀區域，并逐級在較高分辨率圖像的窄帶狀區域分割，直至得到原分辨率圖像的分割結果；文獻[21]將圖割技術與分水嶺算法相結合進行分割，先用分水嶺將圖像分成若干小的區域，再對這些小區域采用圖割技術，提高了分割速度。

文獻[22]將圖割與主動輪廓相結合，通過設置初始化輪廓建立輪廓區域，利用圖割全局能量最優在一定的輪廓區域尋找目標邊界的最優解；文獻[23]提出圖割計算測地線和最小表面的方法，通過建立網格圖及設置邊緣權使得割的代價任意接近相應輪廓的長度或表面面積。

圖割可用于3D目標或序列的分割，在文獻[1]中，通過交互式選取若干幀的種子點，采用3D圖對運動目標進行了分割。

圖割技術還在圖像修復、圖像合成、區域融合、多攝像機場景重建、聚類、目標識別、形狀重建等諸多方面都有廣泛的應用，充分表明圖割的應用前景是非常廣泛的。

3 能量函數的構造及求解

一個圖像分割的問題可以看做給圖像中所有的像素分配一系列對應標號的問題。如對于一個二值標號的問題，如果像素點i屬于前景，設其標號值為1，反之，如果像素點i屬于背景，設其標號值為 0，這樣通過對像素標號實現對圖像前景和背景的分割。在不確定的情況下，找到最好的標號成為一個優化問題。優化的方法通常由兩步構成：構造能量函數及求解能量函數的最優解。

3.1 能量函數的構造

圖割是解決優化能量函數問題的，因此需要將要解決的問題構造成能量函數，這是前提。

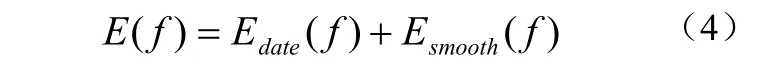
在圖像分割問題中，能量函數的構造包含兩個通常的約束：數據項約束和平滑項約束公式（4）其中數據項Edata(f)對應t-links，它評價分配一個標簽到給定區域的懲罰；光滑項 Esmooth(f)對應n-links，評價兩個相鄰像素不同區域的懲罰，即邊界不連續性。

然而對于具體問題來說，可以在這兩項的基礎上加上符合自己問題的約束條件。例如：基于Potts模型的能量形式公式（5）

式中，E（.）是能量，p和q是像素， N是像素的連通鄰域點集合； Dp(·)是一個數據補償函數，表示數據約束，用于保證每個像素盡可能地找到其對應標號；V{p,q}是平滑項，是對相鄰像素標號不一致的懲罰，V{p,q}通過衡量像素之間的不連續性來決定空間一致性。

在二元標號問題中，即將圖像分為目標和背景兩部分的情形，能量函數得公式（6）

其中f是一個從像素集p到標號集L{0,1}的映射值，對每個像素點給定一個標號值f，f值為0的像素集設定為目標，f值為1的像素集設定為背景。

在加入形狀先驗知識的分割問題中，基于potts模型的能量函數得公式（7）

在圖像修復中，基于Potts模型的能量函數得公式（8）

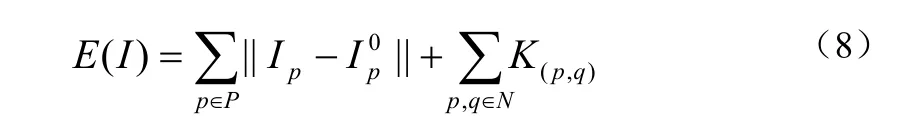
3.2 能量函數的求解

對公式（5）這種組合優化問題，找到全局最優值是一個難以解決的問題。

1956年，ford[24]等證明了著名的最大流/最小割定理，即在任何網絡圖中，最大流的值等于最小割的容量，并給出了求解的具體算法，該算法可以依據多項式時間完成計算；1989年，Greig[23]等人首先發現最大流/最小割算法，能被用來最優化某些重要的能量函數，并根據公式（5）的結構，建立了具有兩個終點的一個圖，使圖的最小割給出了全局最優的二元標號。目前，解決最大流常用Ford-fulkerson算法、push-relabel算法及Boykov等人的新算法。

總之，采用圖割求解能量函數的基本思路，就是對一個給定的能量函數構造對應的網絡圖，然后通過對網絡圖的最小割求解，使得能量函數最優。

4.基于圖割提取圖像信息的解題步驟

綜上所述，基于圖割提取圖像信息的解題步驟，一般為：根據問題建立能量函數、構造有兩個終端節點的網絡圖、用最大流（最小割）算法求解、提取圖像信息，如圖2所示：

圖2 圖割解題步驟

其中最關鍵的步驟，就是根據圖像分割問題，建立合適的能量函數及對能量函數求解。

4.1 建立能量函數

能量函數的建立，主要體現在數據項和光滑項的建立上。典型應用圖割對圖像分割的不同只在數據項和光滑項的定義上。

4.1.1 數據項的建立

圖割在不同領域的應用，主要體現在數據項的建立上。在不同的應用與問題中，數據項的定義不一樣。

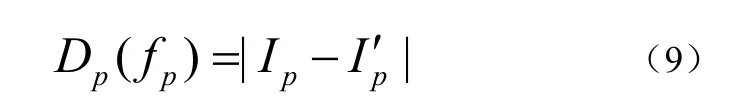
4.1.2 光滑項的建立

如式（3），V{p,q}是光滑項，它是所有相鄰像素的相鄰交互函數的和。光滑項的建立可以提高圖像分割的質量，V{p,q}的形式決定光滑先驗信息的類型，其主要類型有：處處光滑、分段常數及分段光滑。

處處光滑約束的常用形式得公式（10）

分段常數約束的常用形式得公式（11）

分段光滑約束的常用形式得公式（12）

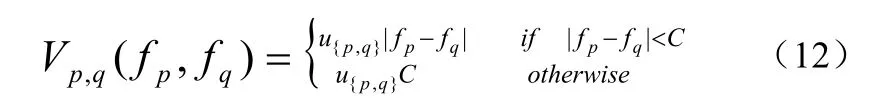
對上式中的系數u{p,q}可根據具體問題做相應的設置。在公式（12）式中，當u{p,q}為常數時，式中的光滑能量為potts能量，光滑項給出了兩個相鄰像素為不同標號時的懲罰，這個懲罰不依賴于設置的標號。在圖像分割中常采用這樣的約束作為光滑項。

建立了數據項和光滑項后，就可建立能量函數。綜上所述，在圖像分割中，常用的能量函數為如下的potts模型，如公式（13）

其中T(·)是指示函數，括號中的值為真，它為1，否則為0。k(p,q)表示對相鄰像素標號不一致的懲罰。

4.2 構造網絡圖

如圖3所示：

圖3 網絡圖

構建一個圖表示這個能量，每個像素看作除表示目標和背景節點外的圖節點，數據項實現每個像素都連接到目標和背景節點，非負邊緣權重 Rp(O)和Rp(B)表示目標和背景區域存在相似像素P。最后，光滑項實現每對相鄰像素(p ,q)的連接，非負邊緣權重 B(p,q)決定邊緣不連續的處罰。由此可見，基于能量函數可以建立網絡圖。

文獻[29]研究了能量函數進行圖割優化應該具備的條件，并給出了具體構造圖的方法。

4.3 求解網絡圖

對于建立的網絡圖G，可通過最大流/最小割算法求解，即求取該網絡的最小割，由于最小割是沿著邊界的總數，最小割的加權圖分割表示從背景分離最好的目標。這樣對能量函數的最優解是通過圖的最小割實現的。

4.4 獲取圖像的處理結果

最小割準則將圖像分割成兩個區域。對于二元標號，通常可直接將一個區域作為目標，另一個區域作為背景。顯然對圖像的二元分割可直接采用圖割方法來獲取全局最優解。

5 存在的問題和研究前景

圖割是基于圖論的圖像分割方法，且具有二元全局能量最優化的特性，盡管它廣泛地應用于圖像分割，但它在分割對象具有弱邊緣、雜波及部分被遮擋時容易失敗，合并形狀先驗信息可防止這樣的失敗，然而將這樣的信息融入圖割是一個長期的研究領域。

目前，基于圖割的交互式分割得到了良好的分割結果與廣泛應用，但是基于圖割對圖像進行自動分割以及對運動目標自動分割，還沒有太多研究與應用，因此，解決該問題是研究的方向之一。

圖割是基于能量優化的方法，而現有的許多基于能量函數優化的圖像分割方法，都具有其各自的特性和不足。因此，為克服現有方法的不足，如何將現有的方法與其它基于能量的優化方法相結合，或者重建一個新的模型，在一定程度上取長補短是需要研究的問題之一。

隨著圖割在計算機視覺中的廣泛應用，圖割方法本身也存在許多有待改進的不足之處，其中最重要的就是能量函數的更新和最小化問題。利用圖割解決問題要利用網絡圖，而構圖時的計算量過大是一個難題，目前，許多算法已針對圖割方法構圖時計算量過大問題進行了改進，把圖割理論和其他方法結合，用于圖像分割可達到很好的效果，如何找到更好的方法解決該問題，是我們努力的一個方向。

正則性是函數可以用圖表示的必要條件。只給出了F3集合中函數的構造[23]。至于在 F4，F5，…，Fk集合中，如果函數也滿足正則性，圖割法是否仍然適用，是應該思考的問題。

圖割對應的是二元標號優化問題，而Multiway cut對應多元標號的問題，對它的能量最優求解是一個 NP-Hard問題，目前對Multiway cut的能量最優化采用近似求解，如α-βswap算法和α-expansion算法。這種近似算法，目前多用于計算機視覺的其他方面，在圖像分割中很少應用。如何更好地應用此類算法，解決圖像分割是需要研究的問題。

6 結束語

基于圖割的圖像分割，作為目前國際上圖像分割領域的一個新的研究熱點，因其具有獨特的結構，得到了很多研究者的青睞，并得到了廣泛的應用。然而正因為它是一種新的圖像分割方式，對它的研究和應用還處于初級階段，仍有大量的問題有待研究和解決。基于圖割的圖像分割技術涉及到的理論知識和學科比較廣泛，對其研究不僅可豐富圖像分割的應用，而且在圖像處理領域具有重要的理論價值和巨大的應用潛力，在學科交叉的研究與應用上也具有重要的意義。

[1]Boykov Y,Jolly M P.Interactive organ segmentation using graph [C]cuts.In:Proc.Third International Conference on Medical Image Computing and Computer-Assisted Intervention,2000,276-286.

[2]Yuri Boykov,Olga Veksler.Graph cuts in vision and graphics theories and applications.In [K]Handbook of Mathematical Models in Computer Vision,Springer,2006.

[3]Greig,D.Porteous, B.A.Seheult.Exact maximum a Posteriori estimation for binary images[J], JOumal of the Royal Statistieal Society: SeriesB, 1989, 51(2): 271一279.

[4]Boykov, Y.Jolly, M, P.Interactive Graph cuts for optimal boundary ®ion segmentation of objects in N-D images.[C]Proceedings of “intimation conference on computer vision”, Vancouver, 2001（7）: 105-112

[5]Rother, C.Kolmogorov, V.A.BLAKE.GrabCut:interactive foreground extraction using iterated graph cuts[C], proceeding of the 2004 SIGGRAPH conference，Aug 2004，I：309-314.

[6]Xu, N.Abuja, N.Bansal.R.Object segmentation using graph cuts based active contours[J].computer vision and image understanding，2007,107(3):210-224.

[7]Malcolm, J.Rathi, Y.and Tannenbaum.A.Graph cut segmentation with nonlinear shape priors.[j]In ICIP,2007.1

[8]徐秋萍，郭敏，王亞榮.基于圖割的目標提取實時修正算法.[j]計算機應用.2008(12):28(12),3116-3122.

[9]Ford L R,Fulkerson D R.Maximal flow through a network.[M]Canadian Journal of Mathematics, 1956, 8(3):399-404.

[10]Cherkassky B V,Goldberg A V.On implementing the push-relabel method for the maximum flow problem.[M]Algorithmica.1997,19(4):390-410.

[11]Boykov Y, Kolmogorov V.An experimental comparison of min-cut/max-flow algorithms for energy minimization[C]in vision.IEEE Transactions on Pattern Analysis and Machine Intelligence.2004,26(9):1124-1137.

[12]Hochbaum D.S.The Pseudoflow algorithm:A new algorithm for the maximum flow problem.Operations Research to appear.Extended abstract in The pseudoflow algorithm and the pseudoflow-based simplex for the maximum flow problem.[G]Proc.Int'l Conf.Integer Programming and Combinatorial Optimization, 98:325-337.

[13]Hochbaum D.S.The Pseudoflow algorithm:A new algorithm for the maximum flow problem.[M]Operations Research,2008,58(4):992-1009.

[14]Juan O,Boykov Y.Active graph cuts.Proc.of IEEE Conference on Computer Vision and Pattern Recognition.[C]New York:IEEE Computer Society,2006: 1023-1029.

[15]Rother C, Kolmogorov V,Blake A.GrabCut:interactive foreground extraction using iterated graph cuts.[j]ACM Transactions on Graphics(TOG),2004,23(3): 309～314.

[16]劉嘉，王宏琦.一種基于圖割的交互式圖像分割方法.[j]電子與信息學

[17]楊昌俊，楊新..基于圖割與快速水平集的腹部CT圖像分割..[j]CT理論與應用研究.2011(3): 291-300

[18]吳亞東，孫世新，張紅英等.一種基于圖割的全變差圖像去噪算法.[j]電子學報.2007(2):35(2),265-268.

[19]Herve Lombaert,Yiyong Sun,Leo Grady,et al.A multilevel banded graph cuts method for fast image segmentation.Proceedings of the Tenth IEEE International Conference on Computer Vision, [C]ICCV 2005,1:259-265.

[20]Li Y,Sun J,Tang C K,Shum H Y.Lazy snap-ping.[C]In Proceedings of ACM SIGGRAPH, ACM Press, 2004,23(4):303-308.

[21]Xu N,Bansal R,Ahuja N.Object segmentation using graph cuts based active contours.[C]In IEEE International Conference on Computer Vision and Pattern Recognition,2003,2:46-53.

[22]Greig D,Porteous B,Seheult A.Exact maximum a posteriori estimation for binary images.[C]Journal of the royal statistical society,series B.1989,51(2): 271-279.

[23]Slabaugh G.and Unal, G.“Graph cuts segmentation using an elliptical shape prior,” in Int.Conf.[G]on Image Processing, 2005, pp.1222-5.

[24]D.Freedman and T.Zhang, “Interactive graph cut based segmentation with shape priors,” [j]in Computer Vision and Pattern Recognition, 2005, pp.755-762.

[25]Das, P.Veksler, O.Zavadsky, V.and Boykov, Y.“Semiautomatic segmentation with compact shape prior,”in Canadian Conf.[j]on Computer and Robot Vision,2006, pp.28-36.