IFF應(yīng)答信號(hào)實(shí)時(shí)檢測技術(shù)

趙 琨，何玉紅

(1.西安電子科技大學(xué)，陜西西安 710071;2.中國電子科技集團(tuán)公司第五十四研究所，河北石家莊 050081)

0 引言

無源被動(dòng)探測系統(tǒng)通過接收、分析目標(biāo)發(fā)射的電磁信號(hào)來確定目標(biāo)的各類參數(shù)，自身不需要發(fā)射電磁信號(hào)，因此許多國家都開始發(fā)展無源探測技術(shù)。IFF系統(tǒng)作為現(xiàn)代戰(zhàn)爭中識(shí)別敵我的一種重要手段，廣泛裝備于軍用飛機(jī)、艦艇等作戰(zhàn)武器平臺(tái)，同時(shí)也安裝在民用飛機(jī)上，用于空中交通管制。IFF系統(tǒng)的廣泛使用，也使得IFF信號(hào)成為無源被動(dòng)探測的主要目標(biāo)之一。通過對(duì)IFF信號(hào)的實(shí)時(shí)檢測與測量，可以為無源被動(dòng)探測提供有利的數(shù)據(jù)，進(jìn)行目標(biāo)識(shí)別、定位和跟蹤等，而這些功能都對(duì)實(shí)時(shí)性的要求非常高，因此，該文將對(duì)IFF系統(tǒng)應(yīng)答信號(hào)實(shí)時(shí)檢測技術(shù)進(jìn)行分析。

1 IFF應(yīng)答信號(hào)特征

IFF信號(hào)屬于二次雷達(dá)信號(hào)，用固定點(diǎn)頻進(jìn)行詢問和應(yīng)答，詢問頻率為1030 MHz，應(yīng)答頻率為1090 MHz，主要用于對(duì)雷達(dá)檢測到的目標(biāo)進(jìn)行屬性判別。其詢問和應(yīng)答脈沖采用脈沖幅度調(diào)制(PAM)，不同工作模式的IFF信號(hào)的脈沖寬度、脈沖間隔及框架脈沖結(jié)構(gòu)不同，不同目標(biāo)發(fā)射的IFF信號(hào)則可通過信息碼進(jìn)行區(qū)分。因此，通過對(duì)IFF信號(hào)的實(shí)時(shí)檢測和測量，得到脈沖寬度和間隔，即可進(jìn)行模式識(shí)別和多目標(biāo)分選，獲取其輻射源目標(biāo)的有關(guān)信息。典型的信號(hào)時(shí)域波形如圖1所示。

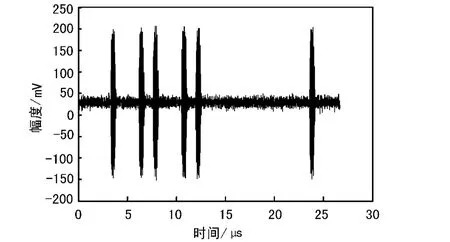
圖1 典型IFF應(yīng)答信號(hào)時(shí)域圖

IFF應(yīng)答信號(hào)的載頻為已知的1090 MHz，它是一系列的短脈沖序列經(jīng)過載波調(diào)制而成。常見的幾種IFF應(yīng)答信號(hào)規(guī)格與技術(shù)參數(shù)如表1所示。

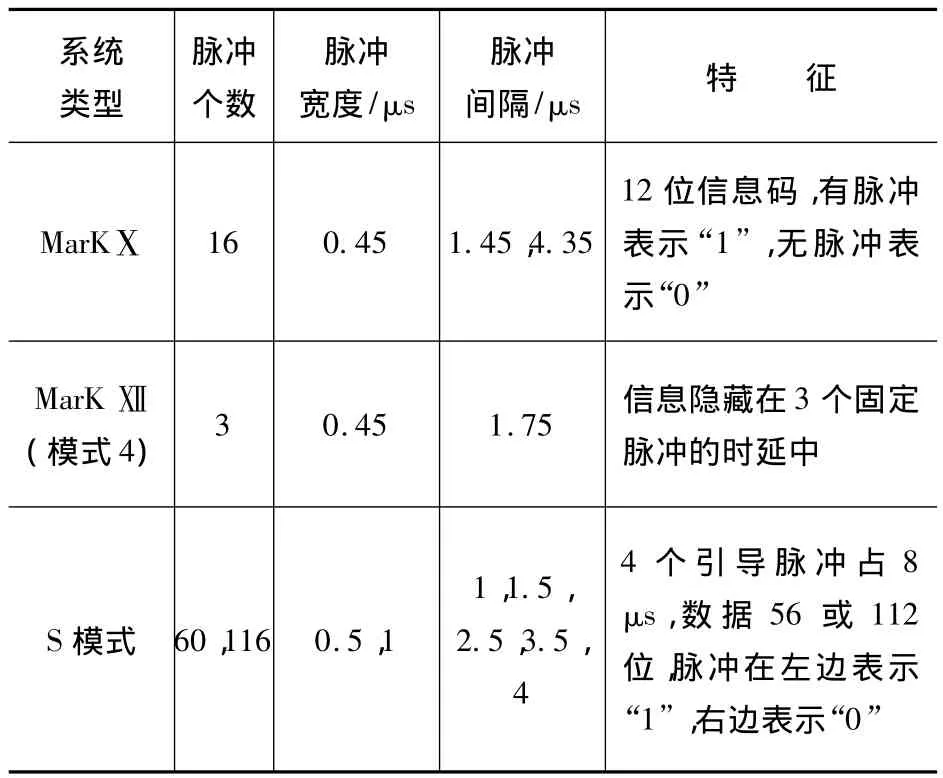
表1 IFF應(yīng)答信號(hào)參數(shù)

IFF應(yīng)答信號(hào)的數(shù)學(xué)表達(dá)式為:

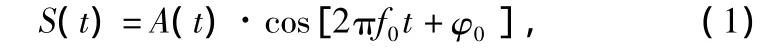
式中，A(t)為IFF信號(hào)的基帶脈沖序列，f0為載波頻率，φ0為載波初始相位。經(jīng)過中頻采樣后得到的敵我識(shí)別信號(hào)表達(dá)式為:

從式(2)可以看出，只要提取出脈沖信號(hào)的包絡(luò)函數(shù)A(n)，并測量其到達(dá)、結(jié)束時(shí)間，即可得到脈沖寬度和脈沖間隔等參數(shù)，如圖2所示。

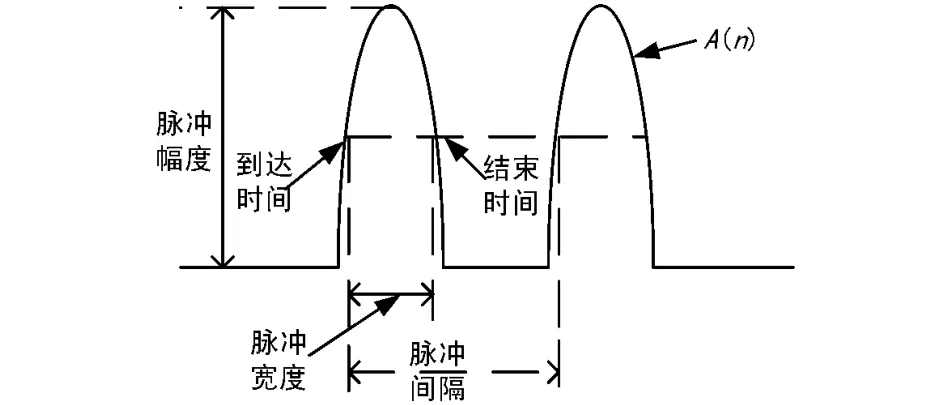
圖2 脈沖參數(shù)

2 IFF應(yīng)答信號(hào)實(shí)時(shí)檢測技術(shù)

根據(jù)IFF應(yīng)答信號(hào)特征，采用基于零中頻的時(shí)域信號(hào)檢測技術(shù)進(jìn)行實(shí)時(shí)脈沖檢測，具體流程如下:中頻輸入信號(hào)經(jīng)模數(shù)轉(zhuǎn)換(A/D)、抗混疊濾波和包絡(luò)檢波后，與本地設(shè)置好的檢測幅度門限進(jìn)行比較(信號(hào)初測)，當(dāng)判定有超過門限的信號(hào)存在時(shí)，則進(jìn)行脈沖信號(hào)的精確參數(shù)測量(包括脈沖幅度、到達(dá)時(shí)間和脈沖寬度)，根據(jù)脈沖寬度進(jìn)行第2次判決，最后輸出符合敵我識(shí)別信號(hào)特征的脈沖參數(shù)，為脈沖信號(hào)模式識(shí)別、多目標(biāo)分離和解調(diào)等后處理提供數(shù)據(jù)，如圖3所示。

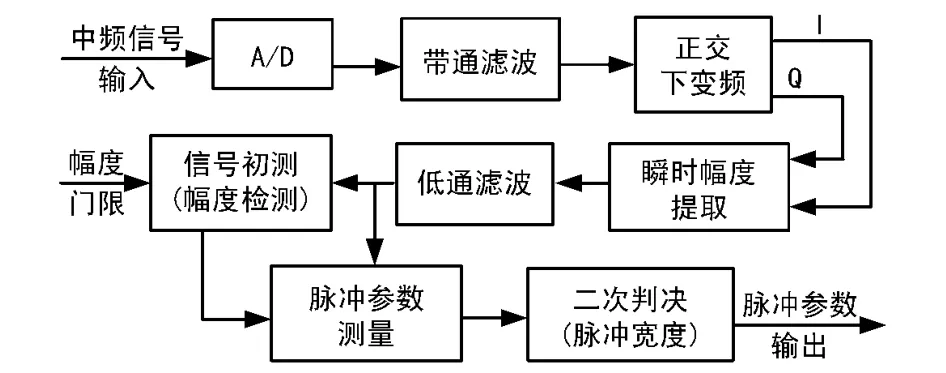
圖3 IFF應(yīng)答信號(hào)實(shí)時(shí)檢測流程

由于信號(hào)檢測對(duì)實(shí)時(shí)性的要求很高，適合用FPGA進(jìn)行工程實(shí)現(xiàn)。因此，在設(shè)計(jì)中不僅要考慮如何快速準(zhǔn)確地提取脈沖信號(hào)參數(shù)，還要考慮算法在硬件電路中的可實(shí)現(xiàn)性。下面就IFF應(yīng)答信號(hào)實(shí)時(shí)檢測及參數(shù)測量技術(shù)中的幾個(gè)關(guān)鍵問題進(jìn)行討論。

3 實(shí)時(shí)檢測關(guān)鍵技術(shù)

3.1 正交下變頻

從一個(gè)實(shí)信號(hào)的解析表示(正交分解)可以很容易獲得信號(hào)的瞬時(shí)幅度，因此，首先采用正交下變頻技術(shù)將中頻信號(hào)轉(zhuǎn)化為解析信號(hào)。數(shù)字信號(hào)的正交變換可以采用數(shù)字混頻的方法:采樣序列X(n)與2個(gè)正交序列cos(ω0n)和sin(ω0n)相乘，再進(jìn)行低通濾波，這種方法適合于信號(hào)中頻變化的情況，并且實(shí)現(xiàn)中占用硬件資源較多。IFF應(yīng)答信號(hào)在載頻是固定的，因此，可以采用基于多相濾波的數(shù)字正交變換方法得到其解析信號(hào)。基于多相濾波的正交變換方法，不需要數(shù)字混頻器，多相濾波器的階數(shù)也比混頻后的低通濾波器少，非常適合工程應(yīng)用。該方法需要輸入信號(hào)頻率f0與采樣頻率fs有式(3)所示的關(guān)系:

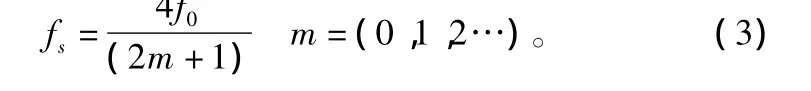
基于多相濾波的正交變換算法實(shí)現(xiàn)方法如圖4所示，詳細(xì)推導(dǎo)過程見參考文獻(xiàn)［1］。

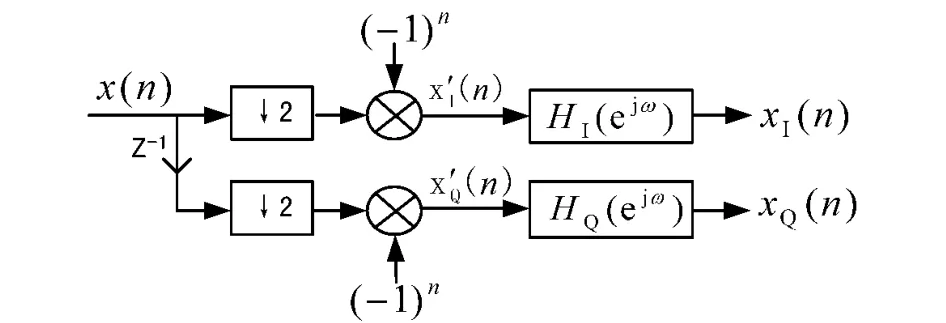
圖4 正交變換的多相濾波實(shí)現(xiàn)

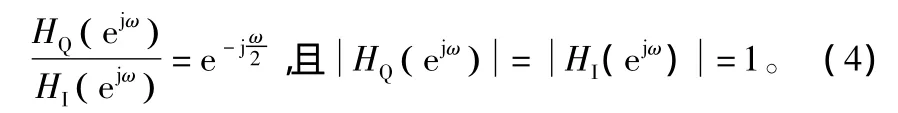
3.2 包絡(luò)檢波

包絡(luò)檢波的目的是提取信號(hào)的瞬時(shí)幅度信息。經(jīng)過正交下變頻后，得到I、Q兩路零中頻正交信號(hào):

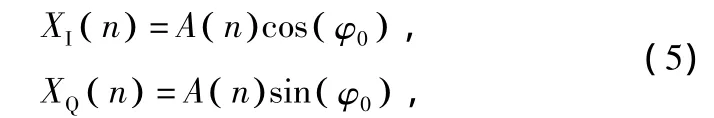
對(duì)這2路信號(hào)求模值:

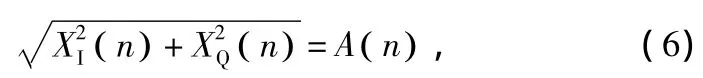
再經(jīng)過低通濾波，濾除高頻分量帶來的抖動(dòng)，就可以得到較為平滑的信號(hào)包絡(luò)A(n)。

IFF信號(hào)的檢測對(duì)實(shí)時(shí)性要求很高，需要硬件電路實(shí)現(xiàn)，而式(6)中的運(yùn)算直接用硬件設(shè)計(jì)實(shí)現(xiàn)較為復(fù)雜，因此采用基于坐標(biāo)旋轉(zhuǎn)思想的CORDIC算法［4］。CORDIC算法的基本思想是將一個(gè)旋轉(zhuǎn)過程分解為一系列的旋轉(zhuǎn)，如式(7)所示，將旋轉(zhuǎn)角θ進(jìn)行分解:

式中，{αn}為基本角度集，δn=±1;第n次旋轉(zhuǎn)的角度大小為αn，旋轉(zhuǎn)方向由δn確定;N的大小與逼近程度有關(guān)。理想情況下N=∞，但實(shí)際中進(jìn)行有限次旋轉(zhuǎn)也可以達(dá)到一定的精度。第n次旋轉(zhuǎn)運(yùn)算為:

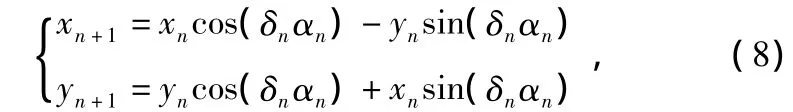
如果選擇角度集為{αn=arctan(2-n)}，那么:

如果不考慮比例因子cos(αn)，CORDIC的基本旋轉(zhuǎn)運(yùn)算可簡化為:

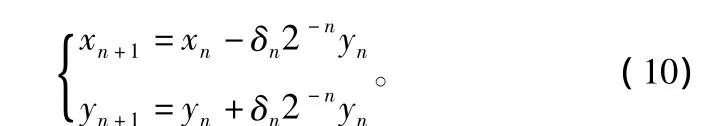
從上式可以看出，第n步旋轉(zhuǎn)運(yùn)算只需移位和加減法運(yùn)算即可，非常適合硬件電路實(shí)現(xiàn)。

3.3 脈沖參數(shù)測量

脈沖參數(shù)測量主要是獲取脈沖信號(hào)的幅度、到達(dá)時(shí)間、結(jié)束時(shí)間及脈沖間隔等參數(shù)，從而為IFF應(yīng)答信號(hào)檢測、模式識(shí)別和多目標(biāo)分選提供依據(jù)。

由于接收到的脈沖信號(hào)強(qiáng)弱不同，取脈沖峰值一半的位置作為脈沖到達(dá)時(shí)間的測量點(diǎn)。此門限隨實(shí)際接收信號(hào)強(qiáng)弱自適應(yīng)變化，因此測量得到的脈沖到達(dá)/結(jié)束時(shí)間更為準(zhǔn)確可靠。

采樣數(shù)據(jù)是時(shí)間離散的，按上述方法計(jì)算出來的脈沖到達(dá)/結(jié)束時(shí)間很可能位于2個(gè)采樣點(diǎn)中間的某個(gè)時(shí)刻，如果粗略選擇較為接近的采樣時(shí)刻作為脈沖到達(dá)/結(jié)束時(shí)間，會(huì)帶來比較大的誤差。由于2個(gè)采樣點(diǎn)間的間隔足夠小，并且從減小硬件設(shè)計(jì)難度方面考慮，可采用在2個(gè)采樣點(diǎn)間線性插值的方法來得到更為精確的時(shí)間。設(shè)A(xa，ya)、B(xb，yb)為2個(gè)相鄰的采樣點(diǎn)，C(xc，yc)為落在A、B兩點(diǎn)之間的脈沖到達(dá)/結(jié)束點(diǎn)。yc已知為脈沖峰值的一半，則求脈沖到達(dá)/結(jié)束時(shí)間的問題歸結(jié)為求xc的值。根據(jù)相似三角形原理有:

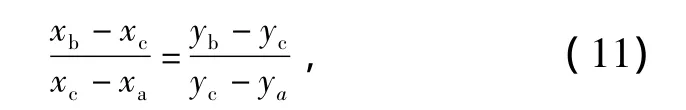
由此得到xc的計(jì)算公式:

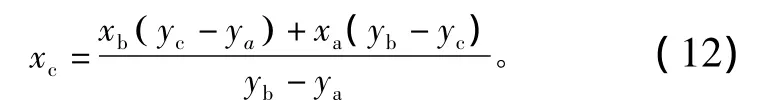
4 實(shí)驗(yàn)驗(yàn)證

由上節(jié)的討論可以看出，IFF信號(hào)實(shí)時(shí)檢測過程的數(shù)據(jù)處理量大，對(duì)速度要求高，但是通過選用適合的算法使得運(yùn)算結(jié)構(gòu)相對(duì)比較簡單，因此適合采樣FPGA實(shí)現(xiàn)。FPGA具有并行工作模式，可同時(shí)兼顧速度及靈活性。FPGA實(shí)現(xiàn)IFF信號(hào)實(shí)時(shí)檢測的流程如圖5所示。

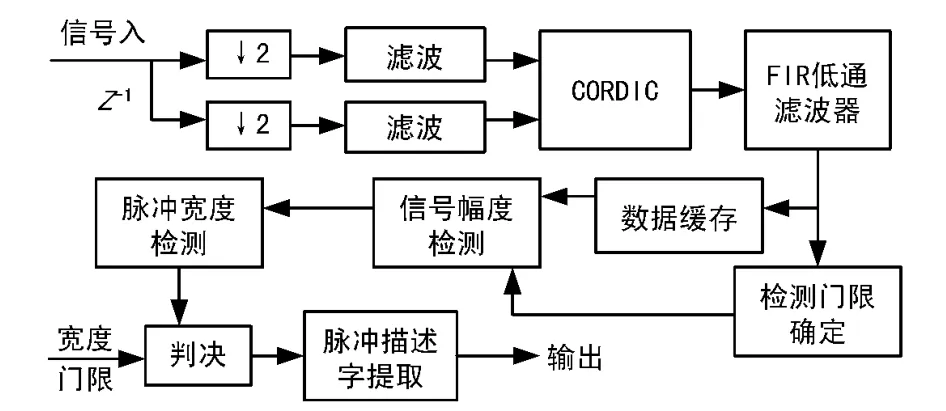
圖5 FPGA實(shí)現(xiàn)流程

采樣信號(hào)經(jīng)過正交下變頻、CORDIC運(yùn)算和低通濾波后得到平滑的脈沖包絡(luò)，利用脈沖包絡(luò)確定信號(hào)檢測門限并進(jìn)行信號(hào)幅度檢測，對(duì)幅度超過檢測門限的信號(hào)進(jìn)一步進(jìn)行脈沖寬度檢測，最終根據(jù)脈沖寬度判定信號(hào)是否IFF應(yīng)答信號(hào)，并提取符合條件的信號(hào)參數(shù)(脈沖描述字)。

以上實(shí)現(xiàn)流程在FPGA中進(jìn)行編程實(shí)現(xiàn)，占用slice資源7188個(gè)。脈沖參數(shù)測量的結(jié)果用于時(shí)差定位系統(tǒng)，得到的時(shí)差測量誤差小于20 ns。

5 結(jié)束語

IFF應(yīng)答信號(hào)實(shí)時(shí)檢測技術(shù)利用基于多相濾波的正交變換得到零中頻I、Q信號(hào);用CORDIC算法簡化了對(duì)FPGA實(shí)現(xiàn)來說相當(dāng)繁瑣的求平方根的過程;取脈沖頂點(diǎn)幅度的一半位置作為脈沖寬度、脈沖到達(dá)時(shí)間的檢測點(diǎn)，并利用線性插值提高時(shí)間測量精度。

［1］江春燕，周勝源，陳星.基于軟件無線電多相濾波的數(shù)字正交變換技術(shù)［J］.電子設(shè)計(jì)工程，2010，18(6):89-90.

［2］孫凌宇，羅靜，屈金佑.混疊敵我識(shí)別信號(hào)分離算法研究［J］.無線電工程，2011，41(1):18-21.

［3］錢眺，玉龍，查榮.IFF信號(hào)的分析與識(shí)別研究.雷達(dá)與對(duì)抗［J］.2008(3):45-47.

［4］胡海華，楊芳，時(shí)華杰.基于CORDIC算法的AM基帶解調(diào)方法［J］.技術(shù)交流，2010(3):39-41.

［5］聞鑫.MK XII敵我識(shí)別系統(tǒng)及其對(duì)抗［J］.艦船電子對(duì)抗，2006，29(5):18-23.

［6］艾名舜，李釗.雷達(dá)脈沖信號(hào)檢測及參數(shù)估計(jì)新方法［J］.無線電工程，2007，37(4):14-36.