基于近似模型的y軸微機械陀螺系統級優化*

呂湘連，何 洋

(西北工業大學陜西省微/納米系統重點實驗室，西安 710072)

優化一直是設計中的一個重要命題。在MEMS設計中也一樣，可行高效的優化方法一直是設計者們追求的目標［1－6］。尤其在系統級設計中，好的優化方法對設計者快速得到滿意設計方案，減少仿真迭代次數都具有非常重要的意義。

一般的優化問題都可以表達成一個通用形式:

優化目標:minf(xi)，(i=1，2，…，n)

約束條件:gk(xi)≤0(k=1，2，…，I)，hj(xi)≤0(j=1，2，…，J)

但是，相比于一般的優化問題，MEMS系統級優化存在很大的特殊之處。MEMS因為其多學科交叉、多域耦合的特點，要得到其優化目標的的函數形式，即得到f(xi)的具體表達形式，是非常困難的。文獻［7］中，通過復雜的公式推導得到了微機械陀螺的優化目標函數——靈敏度與七個待優化參數之間的函數表達式，在此基礎上基于遺傳算法的全局搜索得到了一組理想的優化解。與上述方法類似，即在得到優化目標函數解析表達式的前提下進行優化設計的還有很多［8－11］。

然而，事實上，對于一個MEMS優化問題，優化目標函數表達式的獲得往往不都是這么有經驗可循，而且上述優化方法建立在得到解析的優化目標函數的基礎之上，不是嚴格意義上的系統級優化。而且對于設計工具中的優化模塊而言，需要提供給設計者的應該是一種相對容易操作和實現的優化方法。

為了體現MEMS系統級優化問題和一般優化問題的特殊性，首先需要對當前MEMS系統級模型進行簡單介紹。

1 MEMS的系統級模型

統一建模方法是當前MEMS系統級建模一致使用的方法，該方法采用同一種建模方法和同一種語言，如硬件描述語言，對系統進行建模和描述，因此用一個仿真器即可實現對整個系統的仿真。西北工業大學提出的多端口組件網絡模型(MuPEN)方法，就是基于統一建模方法的思想提出的一種具體系統級建模規范［12］。依此開發的MuPEN模型庫，成為MEMS系統級建模的基礎。

MuPEN方法把MEMS器件按照功能分為多個功能結構部件，并把其建模為參數化多端口組件。各功能結構部件的行為通過組件的端口變量信號表征。通過組件端口的相互聯結形成的網絡，表征整個MEMS器件。多端口組件的端口一般與功能結構部件自由度對應。組件的端口信號之間的關系采用低階常微分代數方程描述，以加快系統的仿真計算速度。

但是，基于MuPEN方法的MEMS系統級仿真，其特征之一在于:系統級行為模擬不是基于顯式表達的解析式完成的，而是通過組件端口的相互聯結形成的網絡，再根據其內部能量和信號流動來完成的，而這一行為往往通過某一仿真平臺，如Saber來實現。這就造成了MEMS系統級優化問題和一般優化問題的不同之處在于:MEMS系統級優化問題的優化目標:minf(xi)，(i=1，2，…，n)，其函數表達式不能直接得到，而在優化問題中，優化目標的函數表達式往往是決定后續優化搜索的基礎。因此，如何直接得到準確的優化目標函數表達式，成為實現MEMS系統級優化問題的關鍵，而本文就探索了一種近似模型的方法來克服這一問題。

2 基于近似模型的MEMS系統級優化方法

基于近似模型的MEMS系統級優化方法，是在給定MEMS器件結構及其待考察性能指標和優化變量的條件下，基于多端口組件庫構建MEMS器件的系統級模型，在試驗設計的基礎上進行系統級仿真，通過對仿真試驗結果進行回歸分析建立待考察性能指標和優化變量之間的函數關系，即近似模型，基于近似模型寫出優化目標和約束條件的數學表達式，對其進行優化并得到優化結果。

該方法最大的特點和效果就是，通過近似模型的獲得，來解決現有MEMS系統級優化問題中優化目標函數不能直接得到的問題。

3 優化實例——y軸微機械陀螺

為了體現本文提出的系統級優化方法的可行性和有效性，作者給出了一個相對簡單的優化實例。圖1分別為一個微機械陀螺的三維結構示意圖和設計參數示意圖。待優化變量包括器件厚度t，梁寬w，梁長l1，l2，l3。各已有幾何參數和材料參數為:質量塊長700 μm，質量塊寬600 μm，材料彈性系數E:130GPa，密度ρ:2 330 kg/m3，泊松比 λ:0.22。作為約束條件，各待優化參數取值范圍為:3 μm≤w≤20 μm，3 μm≤t≤20 μm，50 μm≤l1≤1 000 μm，20 μm≤l2≤1 000 μm，20 μm≤l3≤1 500 μm，且要求l1－l3≥0。

圖1 y軸陀螺結構示意圖和設計參數示意圖

對于該陀螺，我們最關注的性能參數是其驅動模態諧振頻率fx和檢測模態諧振頻率fz盡可能接近從而達到模態匹配的效果，且希望其頻率值在3 000 Hz附近。

在使用本文提出的基于近似模型的方法對y軸微機械陀螺建模時，首先在Saber Sketch中建立器件的多端口組件網絡系統級模型如圖2所示。

由于優化參數有5個，而且各參數的取值范圍比較大，為了使得在有限次計算的情況下獲得更好的采樣數據，本文選用了均勻試驗設計方法，對各參數(因素)選取15個水平，按照U15(155)的均勻試驗設計表選取了15組試驗方案。由于該y軸陀螺的關鍵性能指標分別是驅動模態的諧振頻率fx和檢測模態的諧振頻率fz，這兩個指標也就是該器件的待考察性能指標，因此，對每組試驗方案，在Saber平臺下進行系統級仿真，得到相應的fx和fz值，具體試驗方案和相應的待考察性能指標結果如表1。

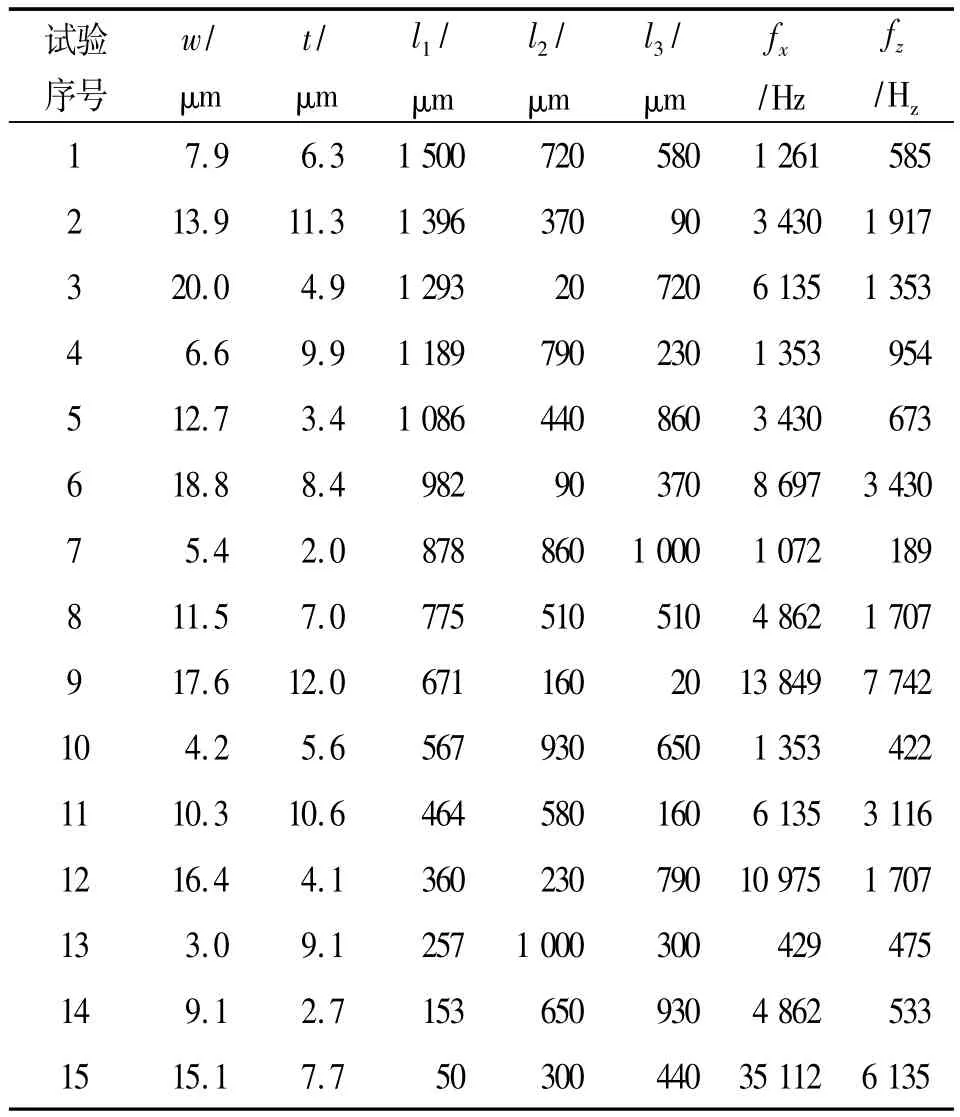
表1 y軸陀螺的均勻試驗設計方案及相應的待考察性能指標結果

因為均勻設計表無整齊可比性，故在均勻試驗設計中需用回歸分析方法來處理試驗數據，通過回歸分析建立待考察性能指標和優化變量之間的函數關系。使用Matlab軟件編程進行回歸分析，分別得到驅動模態的諧振頻率fx與檢測模態的諧振頻率fz與優化變量之間的二次回歸方程，如下:

為了衡量該近似模型和采樣點數據之間的誤差，這里分別計算其誤差向量的 2－范數R2為0.983 8和0.981 9，滿足數據擬合中R2值最好大于0.9的要求，近似模型比較準確的反映了采樣處待考察性能和待優化變量之間的函數關系。

在得到驅動模態的諧振頻率fx與檢測模態的諧振頻率fz與優化變量之間表達式的基礎上，寫出顯式的優化目標函數并不困難:

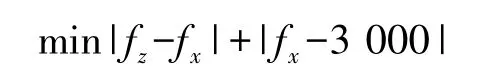
優化目標函數中，|fz－fx|表示驅動模態的諧振頻率fx與檢測模態的諧振頻率fz的差值，|fx－3 000|表示驅動模態的諧振頻率fx與目標值3 000Hz的差值，優化目標是使這兩部分的和最小，也就是使fx與fz差值最小，同時fx在3 000 Hz左右。

結合優化目標和約束條件的數學表達式，采用序列二次規劃算法實現優化。得到的優化結果如表2。

表2 y軸陀螺的優化結果

4 結果及總結

至此，基于近似模型進行y軸陀螺的系統級優化完成。在所得的優化參數下，經過多端口組件網絡的方法進行系統級仿真，得到驅動模態的諧振頻率fx和檢測模態的諧振頻率fz分別為3 074 Hz和2 998 Hz，兩者之間相差76 Hz，較好的實現了模態匹配，且都在3 000 Hz的設計要求附近，約束條件也得到了滿足。該優化方法為提高所設計器件的性能具有參考意義。

［1］John K Coultate，Colin H J Fox，Stewart McWilliam.Application of Optimal and Robust Design Methods to a MEMS Accelerometer［J］.Sensors and Actuators A，2008(142):88－96.

［2］Zhun Fan，Jiachuan Wang，Sofiane Achiche.Structured Synthesis of MEMS Using Evolutionary Approaches［J］.Applied Soft Computing，2008(8):579－589.

［3］Min Liu，Kurt Maute，Dan M Frangopol.Multi-Objective Design Optimization of Electrostatically Actuated Microbeam Resonators with and without Parameter Uncertainty［J］.Reliability Engineering and System Safety，2007(92):1333－1343.

［4］Raulli M，Maute K.Topology Optimization of Electrostatically Actuated Microsystems［J］.Struct Multidisc Optim，2005(30):342－359.

［5］李平，石云波，朱正強.MEMS高g加速度傳感器固有頻率的優化及驗證［J］.傳感技術學報，2010，23(3):388－392.

［6］方華軍，劉理天.壓電折疊梁微執行器的低電壓優化設計［J］.傳感技術學報，2008，21(3):465－468.

［7］Yuan Weizheng，Chang Honglong，Li Weijian.Application Application of an Optimization Methodology for Multidisciplinary System Design of Microgyroscopes［J］.Microsystem Technology，2006，12:315－323.

［8］Papila M，Haftka R T，Nishida T，et al.Piezoresistive Microphone Design Pareto Optimization:Tradeoff between Sensitivity and Noise Floor［J］.Journal of Microelectromechanical System，2006，15(6):1632－1643.

［9］Mukherjee T，Iyer S，Fedder G K.Optimization-Based Synthesis of Microresonators［J］.Sensors and Actuators A，1998，70(2):118－127.

［10］Apolstolyuk V A，Logeeswaran V J，Tay F E H.Efficient Design of Micromechanical Gyroscopes［J］.Journal of Micromechanics and Microengineer，2002，12:48－54.

［11］Han J S，Kwak B M.Robust Optimal Design of a Vibratory Microgyroscope Considering Fabrication Errors［J］.Journal of Micromechanics and Microengineer，2001，11:662－671.

［12］霍鵬飛，馬炳和，苑偉政.基于組件網絡方法的微加速度計建模與仿真［J］.航空學報，2003，24(5):466－470.