不同建模假定下巖石損傷黏彈模型的參數轉換關系探討

方 燾，劉新榮，黃 明

（1.重慶大學 土木工程學院，重慶 400045；2.華東交通大學 土木建筑學院，南昌 330013；3.重慶大學 山地城鎮建設與新技術教育部重點實驗室，重慶 400045；4.福州大學 土木工程學院，福州 350108）

1 引 言

目前，針對巖石蠕變本構模型的研究已經取得了較大的進展，并獲得了較豐富的研究成果[1－3]。對于元件組合模型的應用，單軸蠕變試驗時模型的彈性參數常選用拉壓模量，而在FLAC3D軟件中對三維工程進行模擬計算時一般采用剪切模量，因此，針對工程應用或三維數值計算中的需要，有必要進行一維狀態下巖石蠕變模型的三維狀態推廣研究。通常情況下，蠕變方程由一維轉化到三維時存在不同的建模思路，不同的建模思路對應的模型參數并不相同，需要建立轉換關系。因此，本文將從巖石的一維損傷黏彈性模型分析入手，將其推廣到復雜應力狀態，建立三維狀態下巖石損傷黏彈性模型，并探討其參數的轉換關系。

2 巖石的一維損傷黏彈性模型

文獻[4]將 Kelvin模型和 Burgers模型進行綜合，提出可描述巖石單軸蠕變特性的nBurgers模型，如圖1所示，可較好地概括這兩種情況，公式如下：

圖1 nBurgers模型Fig.1 nBurgers model

在受到諸如含水率、溫度變化以及輻射等外界條件影響時，巖石材料的變形特性將受到影響，巖石的蠕變特性將有所改變，筆者認為，在考慮巖石內部的這些外界因素對變形造成的影響時，可將其分為瞬間彈性損傷和長期蠕變損傷這一特性反映到巖石的蠕變模型中時，瞬間彈性損傷階段將根據加載瞬間彈性模量的劣化定義瞬間彈性損傷變量，而長期蠕變損傷階段則根據蠕變模量的劣化定義蠕變損傷變量。

（1）瞬間彈性損傷

對于損傷變量的定義，一種方法是從能量損傷中按彈性模量變化來定義的損傷變量，這種方法認為，材料性質的“劣化”是造成材料損傷的主要因素，借鑒這一思路，在nBurgers模型中，可采用描述瞬間變形特性的彈性元件的變形參數EM的劣化來定義彈性損傷D(w)，有

式中：EM(0)為初始狀態的瞬間變形模量；EM(w)為受外界因素影響后的變形模量；w為含水率。

（2）長期蠕變損傷

與定義瞬間彈性損傷的思路一致，在定義長期蠕變損傷時將根據蠕變模量的變化來進行，認為初始狀態下巖石處于無損狀態，當外部因素影響后，巖石蠕變模量發生衰減，由此可定義蠕變損傷變量D′(w) 為

因此，對于考慮巖石的這種損傷蠕變特性研究時，在nBurgers模型基礎上建立kBurgers模型，如圖2所示，一維情況時，kBurgers模型蠕變方程為

圖2 一維狀態下的kBurgers模型Fig.2 kBurgers model in the case of one-dimensional state

若將模型參數的損傷統一成如下表達式：

由式（6）可得

將式（6）、（7）代入式（5）得 kBurgers模型一維形式為

3 不同假定下巖石損傷蠕變模型的三維推廣

關于三維狀態下的損傷表達式，需要由一維狀態下的損傷表達式拓展而得。因此，在拓展到三維狀態下時，可做出以下設定：（1）巖石損傷的主軸與主應力軸、應變主軸重合；（2）初始狀態損傷為0。把蠕變本構方程擴展到三維狀態，對材料的損傷不考慮材料各向異性的影響，D(w)和D′(w)拓展到三維狀態分別表示為 Dijkl(w)和，各損傷主軸上的損傷度仍可采用一維狀態下損傷度的求法。

3.1 常泊松比假定建模方法

朱伯芳[5]在研究復雜應力和邊界條件下黏彈性介質中的應力和位移與其邊界條件的聯系時，先后提出3個與彈性體相對應的定理，其中第1、第3定理中都是假定蠕變泊松比保持常數且等于彈性泊松比，即 μ(t′)=μ(t,t ′)=μ=常數。

由一維到三維過程，考慮常泊松比條件也存在兩種方法[6]，第1種就是從拉壓狀態的蠕變方程直接推廣到三維狀態，此時模型參數為拉壓蠕變參數，與無任何假定時一維拉壓蠕變參數是一致的；還有一種是通過黏彈性力學中的對應性原理，通過流變本構方程的拉普拉斯變換和逆變換得到對應的三維蠕變方程，此時模型中的參數為剪切蠕變參數，與無任何假定時一維剪切蠕變參數是一致的[7]。

3.1.1 組合模型彈性參數選用拉壓模量

三維應力情況下，考慮材料各向同性的標準線性固體彈性應力-應變關系可表示為[8]

式中：[U]為泊松比的常系數矩陣，表達式為

考慮到黏彈性模型的流變特性，由流變本構方程利用微分算子代換[9]并求解微分方程后得到蠕變方程的基本形式：

對于nBurgers模型，則有

式中：EM、E0、ηk和ηM都是一維拉壓情況下對應的模型參數；開關函數在一維情況下可用H(σ-σk)來表示，而在三維情況下則可用表示：

把式（6）、（7）代入式（12）可得

將式（14）改寫為張量形式：

3.1.2 組合模型彈性參數選用剪切模量

若一維情況下模型參數通過蠕變剪切試驗得到，則模型參數將采用一維剪切蠕變試驗參數，因此，可將模型參數的損傷統一成如下表達式：

故由式（16）可得

結合文[8]在常泊松比假定下黏彈性體的三維建模思路，若模型參數采用剪切蠕變試驗獲得（如圖3所示），則推導可得kBurgers模型的三維張量形式：

式中：μ*為考慮含水影響的泊松比。

因此，基于兩種假定條件下的單軸拉壓蠕變方程可分別通過式（15）和（18）進行變換得到：

圖3 常泊松比假定下的kBurgers模型Fig.3 kBurgers model in the case of static Poisson′s ratio

3.2 常體積模量假定建模方法

物體內一點的應力狀態，可用應力張量表示，即等于體應力張量和偏應力張量之和[11]：

將模型的總應變 εij(t)分解為由偏應力引起的偏應變 eij(t)和體應力產生的體應變εm(t)，即

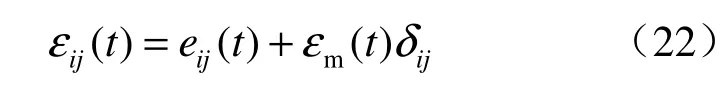
常體積模量假定，即假設黏彈性變形只發生在剪切變形方面，體積變形是彈性的，且假定蠕變過程中體積模量保持常數且等于彈性變形時的體積模量，即 K(t′)=K(t,t′)=K 為常數。

彈性狀態下：

則根據黏彈性問題的對應性原理，黏彈性狀態下有：

式中：J′(t)為蠕變柔量；K為體積模量。

將式（24）代入式（22），得到三維狀態下nBurgers模型蠕變方程的張量形式：

同理，若考慮損傷效應，參數的損傷同樣可以統一表示為

υ(w)和υ′(w)分別為常體積模量建模假定下的彈性損傷變量和蠕變損傷變量。

由式（27）可得：

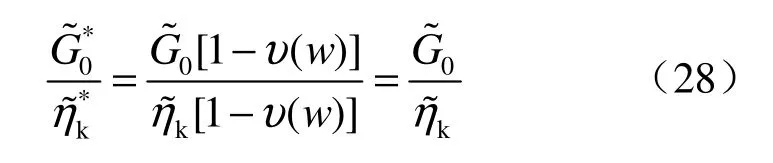
如圖4所示，將式（27）、（28）代入式（26）得kBurgers模型的三維張量表達式：

同樣給出單軸拉壓蠕變情況下的方程，則由式（29）可得：

圖4 常體積模量假定下的kBurgers模型Fig.4 kBurgers model in the case of constant bulk modulus

3.3 各種處理方法模型參數的關系及損傷規律

比較式（8）、（19）、（20）和式（30）可知，不同假定情況下蠕變方程的形式有所不同。常規建模方式與常泊松比假定下模型的一維蠕變方程完全相同，式（8）和式（19）的方程形式及參數一致，說明若模型參數在一維和三維狀態下始終選用拉壓模量，則不考慮任何假定的常規建模方式實質上就是常泊松比假定。

若對同一單軸壓縮條件下的蠕變試驗結果，分別用常泊松比和常體積模量假定下的模型對其進行描述時[6]，則有：

式中：ε1(t)、ε2(t)、ε3(t)分別對應常規建模、常泊松比和常體積模量時的蠕變應變。

于是，常體積模量和常泊松比條件下模型的參數也存在以下對應關系：

式（32）說明，雖然選定的都是一維狀態，但在不同假定條件下組合模型的參數是不相同的。在常泊松比假定下，模型參數需在常規建模的基礎上乘以因子 1/[2(1+μ*)]；常體積模量假定下，不同參數的乘積因子各不相同。

若一維和三維蠕變方程使用的模型參數完全相同，則黏性參數的換算關系也就是常規方式與三維狀態中添加不同假定時黏性參數所需的換算關系，這與習慣上將一維模型的黏性參數直接運用于三維狀態，保持其值不變的做法是不同的。然而，模型參數的這些轉換做法有時也會造成一定的混亂。比較合理的解決方法，一是直接使用包含常體積模量假定的蠕變方程來處理試驗數據，從而保證一維和三維應力狀態的一致性，避開模型參數轉換；二是仍采用常規建模方式來處理蠕變試驗數據，然后利用不同假定下模型參數的變換關系，實現常規建模方式的假設化。

值得思考的是，對于一維拉壓參數轉換至剪切參數時，需要獲得不同狀態下泊松比μ的大小，從而在拉壓蠕變參數轉換成剪切蠕變參數時，求解剪切蠕變參數的損傷方程還應考慮泊松比的影響。因此，在模型參數轉換關系中涉及到泊松比μ時，模型參數的損傷表達式也會變化。例如，反映瞬間彈性變形的參數有如下計算式：

又有，

則由式（33）、（34）可得到以下關系：

式中：μ為初始狀態的泊松比；μ*受外部因素影響后的泊松比。同理可得到模型中其他參數的損傷變量關系式。

4 算例分析

文獻[4]針對 T2b2泥質粉砂巖進行了不同加載等級對應不同含水狀態下單軸蠕變試驗研究，探討了泥質粉砂巖在考慮含水率w變化對巖石蠕變特性的影響，得到了瞬間彈性損傷演化方程：

以及長期蠕變損傷演化方程：

并分析得到了模型三維格式中開關函數的統一表達式：

式中：σ1、σ3分別為最大、最小主應力。

因此，按照以上3種建模方式，不同含水條件下泥質粉砂巖蠕變加載荷載為32 kN時對應的模型參數如表1所示。

表1 3種不同建模方式下不同含水狀態對應kBurgers模型參數反演結果Table1 Parameters of kBurgers model with different moisture contents using three different modeling approaches

常泊松比情況下，參數的損傷變量表達式與常規建模情況相比有下式：

常體積模量假定下有

因此，將試驗得到的泥質粉砂巖不同含水率情況下泊松比μ及不同含水情況下的損傷變量D(w)和D′(w)數值代入式（39）和式（40）得到的計算結果見表2所示。由計算結果可知，蠕變方程的參數隨含水率變化的變化規律有所不同，因而損傷演化規律也不同。對常體積模量假定下模型參數隨含水損傷的演化規律進行分析，結果如圖5、6所示。

得到常體積模量假定下彈性損傷變量方程為

長期蠕變損傷變量方程為

表2 不同含水條件對應kBurgers模型損傷變量Table2 Damage variables of kBurgers model with different moisture contents

圖5 υ(w)與w關系回歸分析結果Fig.5 Regression analysis of υ(w)and w

圖6 υ′(w)與w關系回歸分析結果Fig.6 Regression analysis of υ′(w) and w

5 結 論

（1）將考慮巖石內部含水率變化、溫度變化以及輻射等外界因素對變形造成的影響定義為一種損傷，且包括瞬間彈性損傷和長期蠕變損傷。并根據加載瞬間彈性模量的劣化定義瞬間彈性損傷變量，根據蠕變模量的劣化定義蠕變損傷變量，由此建立考慮損傷的kBurgers模型。

（2）假定泊松比μ為常量，從一維拉壓狀態的蠕變方程入手，轉換得到了常泊松比假定的三維表達式；考慮體積模量K為常數，將黏彈性體的總應變 εij(t )分解為由偏應力引起的偏應變 eij(t)和體應力產生的體應變εii，推導得到了常體積模量的三維表達式。通過對不同假定建模方法得到的模型參數與常規建模模型參數之間的換算關系進行研究，表明不同參數間的換算關系有所不同。

（3）結合算例，對常體積模量假定下模型參數隨含水率變化的損傷演化規律進行了分析，計算得到了常體積模量假定下模型的瞬間彈性損傷和長期蠕變損傷演化方程，且檢驗了不同假定下模型參數間轉換關系的有效性。

[1]夏才初,王曉東,許崇幫,等. 用統一流變力學模型理論辨識流變模型的方法和實例[J]. 巖石力學與工程學報,2008,27(8): 1594－1600.XIA Cai-chu,WNAG Xiao-dong,XU Chong-bang,et al.Method to identify rheological models by unified rheological model theory and case study[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(8): 1594－1600.

[2]徐衛亞,楊圣奇,褚衛江. 巖石非線性黏彈塑性流變模型（河海模型）及其應用[J]. 巖石力學與工程學報,2006,25(3): 433－447.XU Wei-ya,YANG Sheng-qi,CHU Wei-jiang. Nonlinear viscoelasto-plastic rheological model (Hohai model) of rock and its engineering application[J]. Chinese Journal of Rock Mechanics and Engineering,2006,25(3): 433－447.

[3]丁志坤,呂愛鐘. 巖石黏彈性非定常蠕變方程的參數辨識[J].巖土力學,2004,25(增刊1): 37－40.DING Zhi-kun,Lü Ai-zhong. Parameter identification of non-stationary creep equation of rocks[J]. Rock and Soil Mechanics,2004,25(Supp.1): 37－40.

[4]黃明. 含水泥質粉砂巖蠕變特性及其在軟巖隧道穩定性分析中的應用研究[D]. 重慶: 重慶大學,2010.

[5]朱伯芳. 在混合邊界條件下非均質黏彈性體應力與位移[J]. 力學學報,1964,7(2): 162－167.ZHU Bo-fang. The stresses and deformations in the nonhomogeneous visco-elastic media undermixed boundary conditions[J]. Acta Mechanica Sinica,1964,7(2): 162－167.

[6]黃小華,馮夏庭,陳炳瑞,等. 蠕變試驗中黏彈組合模型參數確定方法的探討[J]. 巖石力學與工程學報,2007,26(6): 1226－1231.HUANG Xiao-hua,FENG Xia-ting,CHEN Bing-rui,et al.Discussion on parameters determination of viscoelastic model in creep test[J]. Chinese Journal of Rock Mechanics and Engineering,2007,26(6): 1226－1231.

[7]徐平,李云鵬,丁秀麗,等. FLAC3D黏彈性模型的二次開發及其應用[J]. 長江科學院院報,2004,21(2): 10－13.XU Ping,LI Yun-peng,DING Xiu-li,et al. Secondary development and application of visco-elastic constitutive model in FLAC3Dsoftware[J]. Journal of Yangtze River Scientific Research Institute,2004,21(2): 10－13.

[8]黃小華,馮夏庭. 常泊松比下黏彈性體的算子代換法與黏彈對應原理的關系[J]. 巖石力學與工程學報,2006,25(12): 2509－2514.HUANG Xiao-hua,FENG Xia-ting. Relation between operator substitution of viscoelastic body and elastoviscoelastic correspondence principle with constant Poisson ratio[J]. Chinese Journal of Rock Mechanics and Engineering,2006,25(12): 2509－2514.

[9]孫鈞. 巖土材料流變及其工程應用[M]. 北京: 中國建筑工業出版社,1999.

[10]宋飛. 石膏角礫巖非線性流變模型研究及有限元分析[D].西安: 長安大學,2006.

[11]楊桂通. 彈塑性力學引論[M]. 北京: 清華大學出版社,2004.