埋地管道彎管應力數值計算

吳玉國，周立峰，朱佳琦，李小玲

（1. 遼寧石油化工大學 石油天然氣工程學院， 遼寧 撫順 113001； 2. 中國石油遼河工程有限公司， 遼寧 盤錦 124010）

彎管廣泛應用于管道系統當中，由于其形狀和結構形式的復雜性導致其受力情況也比較復雜，而采用有限元分析方法，能夠得到得到滿足工程精度要求的應力解，為進行彎管結構可靠性分析和壽命分析提供依據［1］。

1 ANSYS12.0及有限元分析

ANSYS軟件作為ANSYS公司開發的有限元計算分析程序，具有強大的、廣泛的分析功能[2,3]。該軟件采用了有限元分析法，有限元方法中一個物體或系統被分解為由多個相互聯結的、簡單的、獨立的點組成的幾何模型。將根據實際的物理模型推導出的平衡方程式使用于每個點上，便產生一個可以用線性代數的方法求解的方程組。

經過離散化處理的的有限元計算模型可以歸結成為如下一線性方程組[4]：

式中： {F} —所受到的外力向量；

［K］—整體剛度矩陣；

{D} —模型中各個節點的位移向量。

［K］由每個單元對應的剛度矩陣疊加得到：

式中：［E］e—單元剛度矩陣。

公式（1）中所受的外力向量的表達式如下：

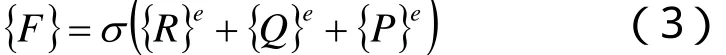
式中：{R}e—單元集中力；

{Q}e—單元表面力；

{P}e—單元體積力。

求出方程（1）中的各個系數并給定具體的邊界條件，待求的有限元模型上各節點的位移{D}就可以被求出。先將單元上各節點的應變{E}求出，{E}=［B］{D}e，其中的［B］代表單元的幾何矩陣，跟具體的單元類型有關系。然后依據彈性方程{R}=［D］{E}就能夠將應力求出。

2 計算模型

一條φ720 mm×8 mm的埋地輸油管線，其管道中心埋深處土壤自然溫度為 15 ℃，內壓為 4 MPa。所用管材的彈性模量為210 GPa，線膨脹系數為 12×10-61/℃[5]。

在建立管道模型時（本文以 90°彎頭為例），管道截面應用plan42單元建立，之后進行相應的網格劃分，在掃描線建立的基礎上使用solid70熱單元做三維單元掃掠，并將plan42單元刪除。經過以上步驟最終得到如圖1所示的模型及其網格。

3 結果分析

3.1 不同溫度下的彎頭應力

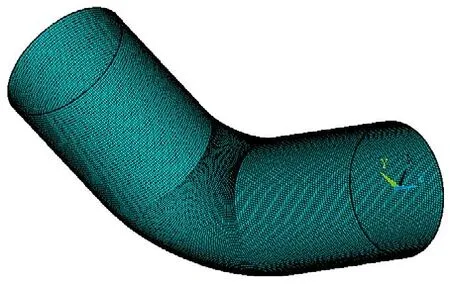
圖 1 彎管模型及其網格劃分Fig.1The bend pipe model and grid

輸油溫度為20 ℃和60 ℃時90°彎頭所受到的應力情況如圖2和圖3所示。

圖2 輸油溫度為20 ℃時彎頭應力分布情況Fig.2 Stress distribution of the elbow when the transporting temperature is 20 ℃

從兩圖中顯示出的彎頭所受熱應力的數值計算結果容易看出，彎頭所受到熱應力值隨著輸油溫度的增加而增大，而且在不同輸油溫度下熱應力具有相同的分布規律：應力主要集中于彎頭的內半徑附近的位置。

3.2 夾角、曲率半徑對彎頭應力的影響分析

彎頭處所受應力還受到彎頭夾角以及彎頭曲率半徑等的影響，為了探尋這些因素對于彎頭所受應力的具體影響規律，非常有必要對不同夾角、曲率半徑下的彎頭所受應力進行計算與分析[5]。本文計算了 20°、60°和 90°的彎頭在曲率半徑R分別為D、2.5D 和 5D 情況下所受的應力。在計算過程中選擇了4結點殼單元，并且沿著圓周方向每15°劃分成1個單元，具體情況如圖4所示。

圖3 輸油溫度為60 ℃時彎頭應力分布情況Fig.3 Stress distribution of the elbow when the transporting temperature is 60 ℃

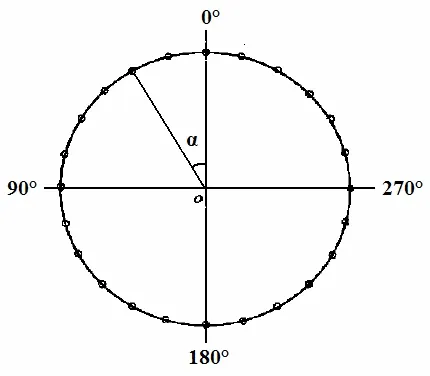
圖4 彎頭橫斷面結點分布Fig.4 The node distribution at cross section of the elbow

所得的計算結果顯示于圖5至圖12，每種計算條件下的計算結果圖均包括兩個，其中的左圖是彎頭所受應力分布云圖，而右圖是彎頭的中間橫截面內壁圓周各點處的應力值和應變值，右圖中的藍色曲線和紅色曲線分別代表的是應力變化曲線和應變變化曲線，圖中的橫坐標代表的意義為沿著逆時針方向距圓周起點間的弧長。

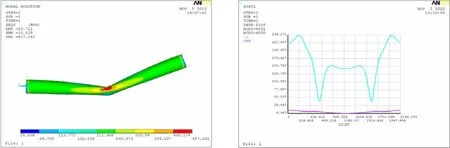
圖5 20°彎頭曲率半徑為D時的應力計算結果Fig.5 Stress of the 20°elbow with Dcurvature radius

圖6 20°彎頭曲率半徑為2.5D時的應力計算結果Fig.6 Stress of the 20°elbow with 2.5Dcurvature radius

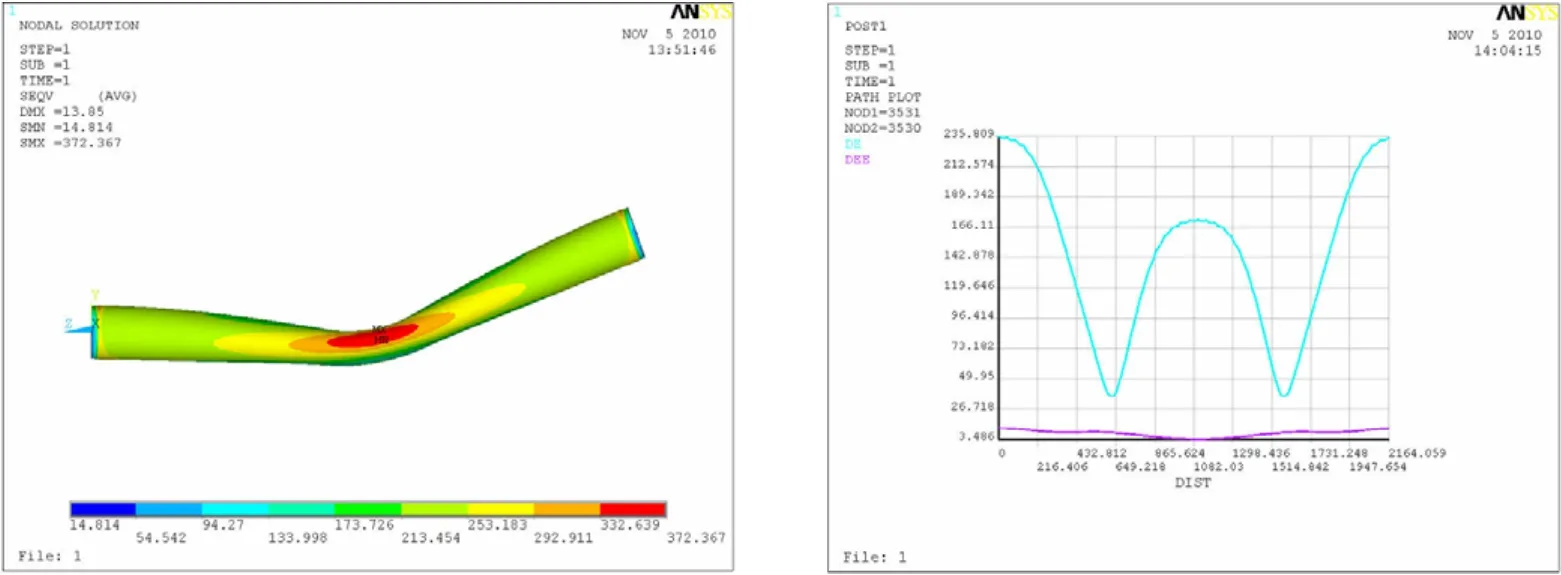
圖7 20°彎頭曲率半徑為5D時的應力計算結果Fig.7 Stress of the 20°elbow with 5Dcurvature radius

圖8 60°彎頭曲率半徑為D時的應力計算結果Fig.8 Stress of the 60°elbow with Dcurvature radius

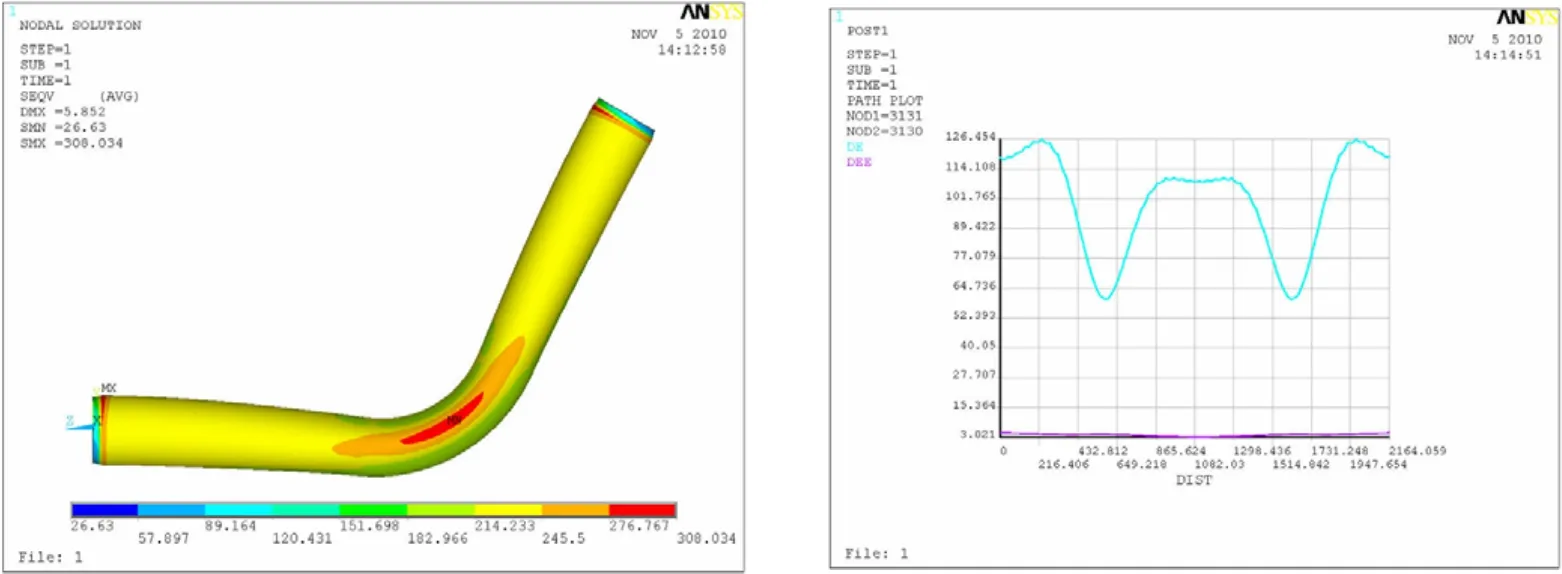
圖9 60°彎頭曲率半徑為2.5D時的應力計算結果Fig.9 Stress of the 60°elbow with 2.5Dcurvature radius

圖10 60°彎頭曲率半徑為5D時的應力計算結果Fig.10 Stress of the 60°elbow with 5Dcurvature radius

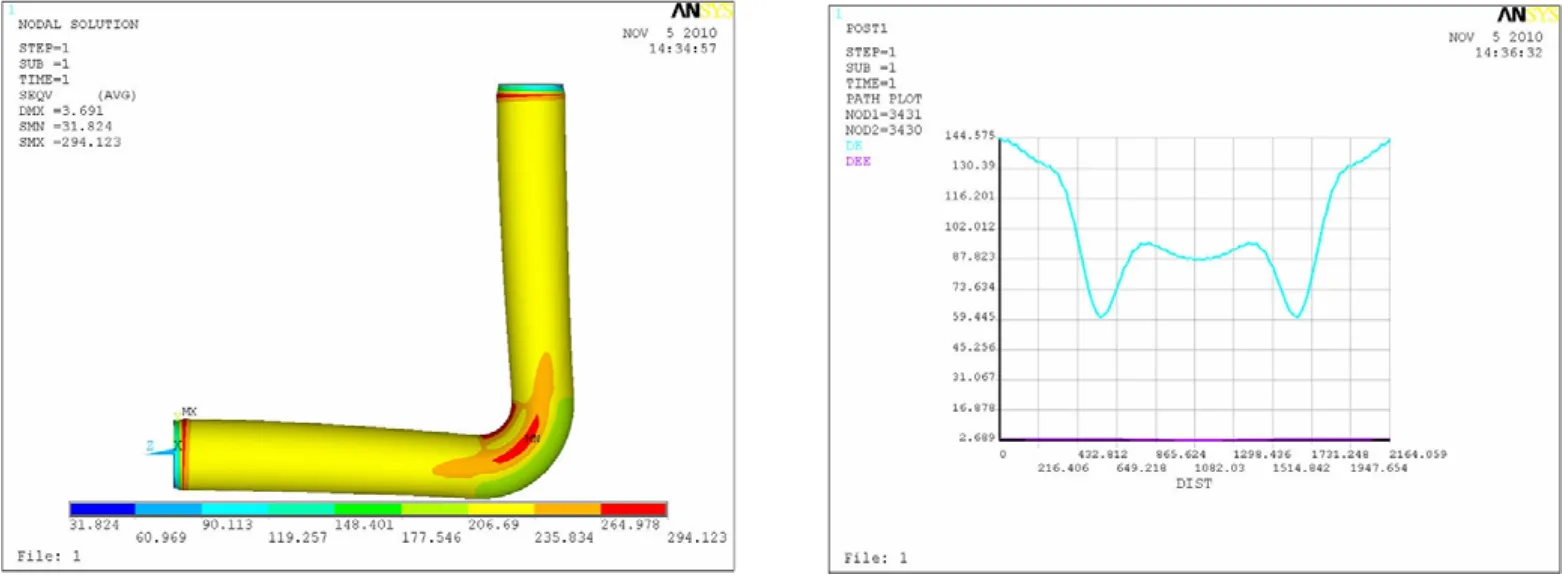
圖11 90°彎頭曲率半徑為D時的應力計算結果Fig.11 Stress of the 90°elbow withDcurvature radius

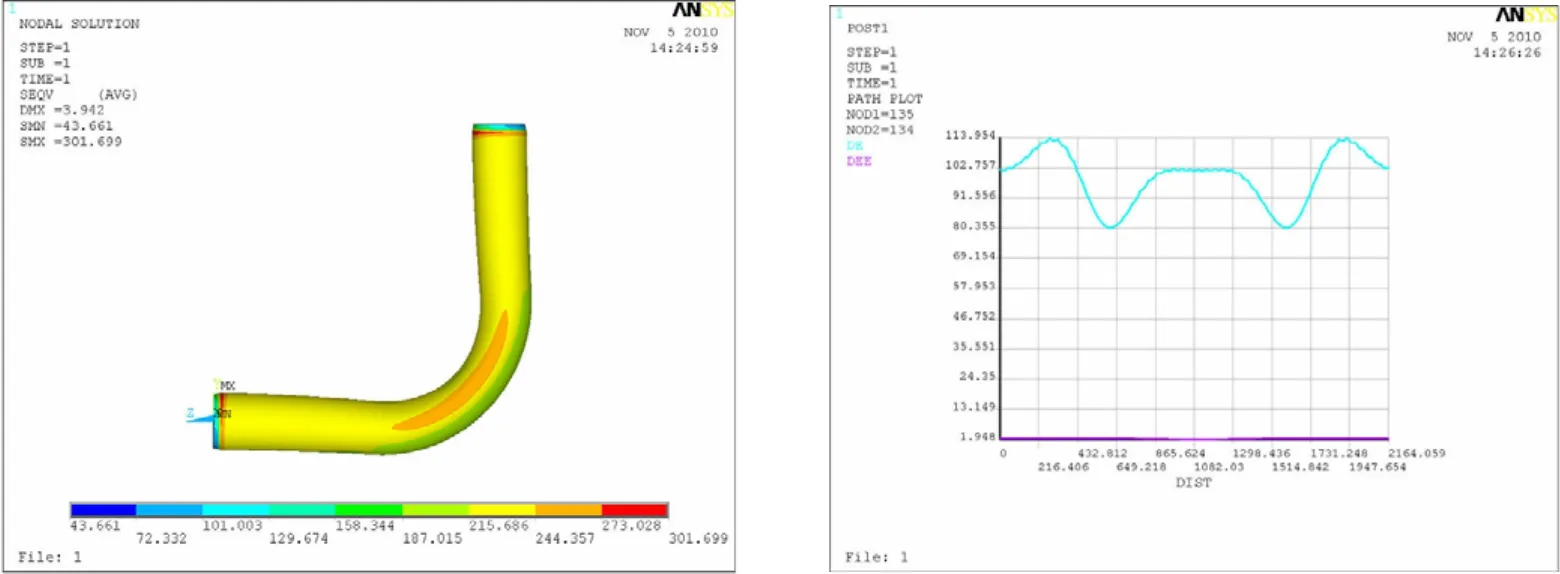
圖12 90°彎頭曲率半徑為2.5D時的應力計算結果Fig.12 Stress of the 90°elbow with 2.5Dcurvature radius

將以上各個計算結果圖進行對比、分析容易得出，在彎頭夾角不變的情況下，彎頭所受應力隨著曲率半徑的增加而減小。

正如圖中所顯示的，對于20°的彎頭，曲率半徑從D變化至5D，相對應的彎頭所受最大的應力值從400 MPa左右降至330 MPa左右；對于60°的彎頭，曲率半徑從D變化至5D，相對應的彎頭所受最大的應力值從 280 MPa左右降至250 MPa左右；對于90°的彎頭，曲率半徑從D 變化至2.5D時，相對應的彎頭所受最大的應力從270 MPa左右降至240 MPa左右。

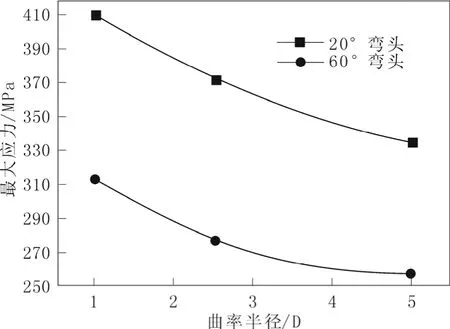
圖13 不同角度彎頭在不同曲率半徑下的應力Fig.13 Stress of the elbows with diffrent angles and curvature radiuses

在彎頭曲率半徑保持不變的情況下，20°的彎頭所受到的最大應力值最大，90°的彎頭所受到的最大應力值則最小。具體數據以曲率半徑均為D 的情況為例，20°的彎頭所受到的最大應力值大約為400 MPa，而90°的彎頭所受到的最大應力值大約為270 MPa。

以上的分析結論可以從圖13中得到更好體現，圖中反映出了不同角度（20°、60°）的彎頭在不同曲率半徑（D、2.5D、5D）條件下彎頭所受最大應力的變化情況。

4 結 語

觀察以上一系列的應力分布曲線圖不難發現，在各種計算條件下的應力分布曲線形狀大體上趨于一致，所以可按其中的一種情況來進行應力分布規律的說明，例如，60°的彎頭在曲率半徑為2.5D時，在圓周位置 30°～40°或 320°～330°位置附近的范圍內呈現出較高的應力水平，在 90°～100°或 260°～270°位置附近的范圍內呈現出較低的應力水平。

［1］ 馬愛梅，鹿曉陽，孫勝.彎管應力分析及結構研究[J].機械設計與制造,2006, 44(3): 98-100．

［2］ 美國ANSYS公司.ANSYS基本過程手冊[R].2002．

［3］ 美國ANSYS公司.ANSYS非線性分析指南[R].2002．

［4］ 劉士民.用ANSYS分析供熱管道彎頭熱應力[J].鹽城工學院學報(自然科學版),2006, 19(2): 26-30.

［5］ 吳玉國.冷熱原油管道順序輸送技術研究[D].青島:中國石油大學（華東）, 2010．