k-階旋轉(zhuǎn)對稱函數(shù)性質(zhì)分析與軌道計數(shù)

李泉，高光普，劉文芬

(信息工程大學(xué) 信息工程學(xué)院，河南 鄭州 450002)

1 引言

1999年，密碼學(xué)者Pieprzyk[1]在研究散列算法的快速實現(xiàn)時提出了旋轉(zhuǎn)對稱函數(shù)的概念。隨著文獻[2~6]等對旋轉(zhuǎn)對稱函數(shù)的進一步分析與研究后，發(fā)現(xiàn)這一類結(jié)構(gòu)特殊的布爾函數(shù)可以具有良好的密碼學(xué)性質(zhì)，并且搜索旋轉(zhuǎn)對稱函數(shù)要比窮盡搜索布爾函數(shù)空間的效率要高，所以一直以來不斷地通過改良搜索旋轉(zhuǎn)對稱函數(shù)空間的方法尋找密碼學(xué)性質(zhì)優(yōu)良的布爾函數(shù)。2006年，密碼學(xué)者Kavut和Yücel[4]利用最速下降法在旋轉(zhuǎn)對稱函數(shù)空間上搜索到的非線性度為241的9元布爾函數(shù)，隨后Kavut和Yücel[7]又證明了241為9元旋轉(zhuǎn)對稱函數(shù)所能達到的最高非線性度。為了得到更好的結(jié)果，2008年，Kavut和Yücel[8]推廣了旋轉(zhuǎn)對稱函數(shù)的概念，提出了k-階旋轉(zhuǎn)對稱函數(shù)，初步搜索出了9元非線性度為242的3-階旋轉(zhuǎn)對稱函數(shù)，并且利用該結(jié)論證明了9元、11元、13元非線性度大于的布爾函數(shù)都是存在的，徹底解決了這個提出近 30年的公開問題。k-階旋轉(zhuǎn)對稱函數(shù)比旋轉(zhuǎn)對稱函數(shù)對布爾函數(shù)代數(shù)結(jié)構(gòu)的約束更低，所以數(shù)量更多，并且已經(jīng)尋找到了比旋轉(zhuǎn)對稱函數(shù)密碼學(xué)性質(zhì)更為優(yōu)良的布爾函數(shù)。

本文在Kavut和Yücel的基礎(chǔ)上研究了k-階旋轉(zhuǎn)對稱函數(shù)的性質(zhì)。首先，證明了k-階旋轉(zhuǎn)對稱函數(shù)的 Walsh譜和自相關(guān)函數(shù)都滿足k-階的旋轉(zhuǎn)對稱。分析發(fā)現(xiàn)k-階旋轉(zhuǎn)對稱函數(shù)的很多性質(zhì)都可以利用其軌道來刻畫，并給出了k-階旋轉(zhuǎn)對稱函數(shù)的軌道中的長圈和短圈的計數(shù)公式。特別取 k =1時，利用本文所得計數(shù)公式與Sarkar和Maitra所得的計數(shù)公式進行比較，發(fā)現(xiàn)Sarkar和Maitra所得的計數(shù)公式在 n = pa1… pal,l =2且存在 a ≥ 2 ，或 l ≥ 3 的1li情況下是不成立的，并分析了原因。

2 基本概念介紹

記二元域｛0, 1｝為GF(2)，定義GFn(2)到GF(2)上 的 函 數(shù) f(x) = f(x1,x2,… ,xn),x=(x1,x2,… ,xn)∈ G Fn(2)為n元布爾函數(shù)。

定義 1[9]n元布爾函數(shù) f (x) ,x∈ G Fn(2)的Walsh譜定義為

定義2[9]設(shè) f (x) ,x∈ G Fn(2)是n元布爾函數(shù)，對x = (x,x ,… ,x )∈ GFn(2), s = (s,s , … ,s)∈ GFn(2),12n12n稱

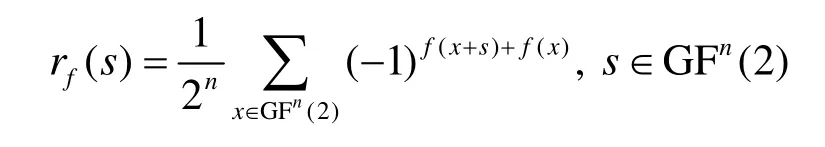
為 f (x)的自相關(guān)函數(shù)。

n元布爾函數(shù)f的自相關(guān)函數(shù) rf和 Walsh譜S(f)有如下關(guān)系：

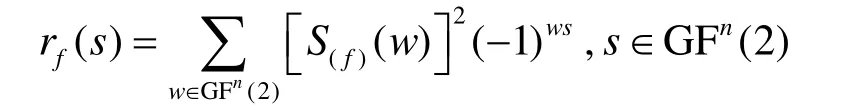
定義3[2]對于任意給定的1≤i≤n,1≤k≤n,xi∈ G F(2)定義

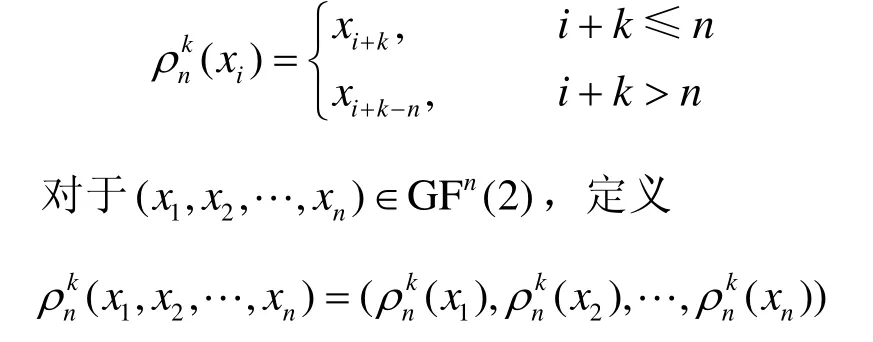
可知， ρnk可視為(x1,x2,… ,xn)的左循環(huán)移位算子。

定義 4[8]對于給定的1 ≤ k ≤ n ,k|n ，n元布爾函數(shù)f對任意輸入的 x = (x,x ,… ,x )∈GFn(2)12n都滿足：

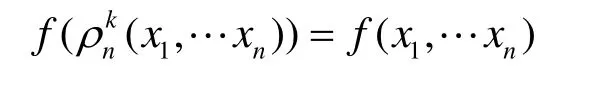
則稱 f為k-階旋轉(zhuǎn)對稱函數(shù)(k-RSBF)。

注 k =1時f即為旋轉(zhuǎn)對稱函數(shù)。

定義 5[2]對于給定的1 ≤ k ≤ n ,k|n 和(x1,…xn)∈ G Fn(2)稱

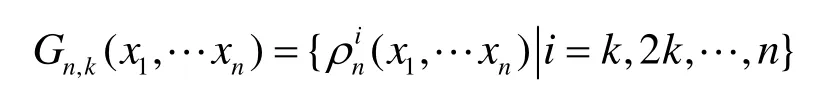
為k-階旋轉(zhuǎn)對稱函數(shù)的軌道，簡稱為軌道。

由定義4可知，對任意的軌道 Gj，k-階旋轉(zhuǎn)n,k對稱函數(shù)限制在該軌道上取值為常數(shù)。將軌道個數(shù)記為將GFn( 2)分成了gn,k個不相交的軌道。顯然，中元素的個數(shù)且都為的因子，稱的軌道為長圈，其個數(shù)記為 h ，稱n,k的軌道為短圈，其個數(shù)記為sn,k。

設(shè) Λ(n,k),j∈ G Fn(2)表示 Gnj,k中元素按字典序排列的第一個元素，稱為軌道 Gnj,k的代表元。k-階旋轉(zhuǎn)對稱函數(shù)的輸出序列可以由長為 gn,k的比特序列

給出，顯然該序列包含著k-階旋轉(zhuǎn)對稱函數(shù)的全部信息。由該序列可知，變元個數(shù)為n的所有k-階旋轉(zhuǎn)對稱函數(shù)的個數(shù)為 2gn,k。

例1 所有4元2-階旋轉(zhuǎn)對稱函數(shù)的軌道為

顯然， Gj的全體代表元為4,2

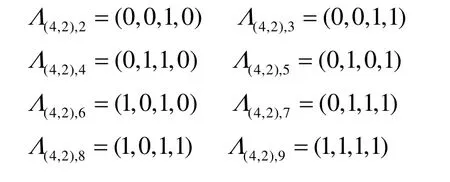
3 k-階旋轉(zhuǎn)對稱函數(shù)的性質(zhì)分析

3.1 k-階旋轉(zhuǎn)對稱函數(shù)的 Walsh譜和自相關(guān)函數(shù)的性質(zhì)

本節(jié)證明了k-階旋轉(zhuǎn)對稱函數(shù)的Walsh譜和自相關(guān)函數(shù)滿足k-階旋轉(zhuǎn)對稱。

引理1[3]對任意給定1≤k≤n、w∈GFn(2)和 x ∈ G Fn(2)都有

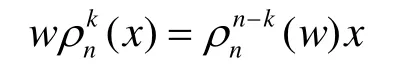
定理1 假設(shè)1 ≤ k ≤ n ,k|n 。則布爾函數(shù)f是n元k-階旋轉(zhuǎn)對稱函數(shù)的充要條件是其 Walsh譜S(f)(w )滿足：

證明 1) 必要性。因為布爾函數(shù) f是k-階旋轉(zhuǎn) 對 稱 函 數(shù) ， 則 對 于 給 定 的1 ≤ k ≤ n ,k|n 有f( ρk( x) ) = f(x)，則n

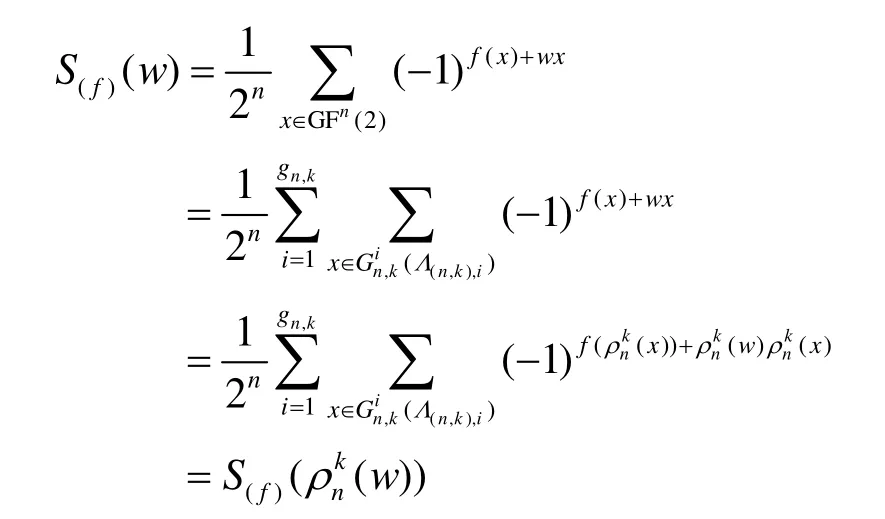
故必要性成立。

2) 充分性。假設(shè)布爾函數(shù) f的Walsh譜 S(f)(w)對 任 意 給 定 的1 ≤ k ≤ n ,k|n , x∈ G Fn(2)和w∈ G Fn(2)滿足,由引理1可知

由反演公式知

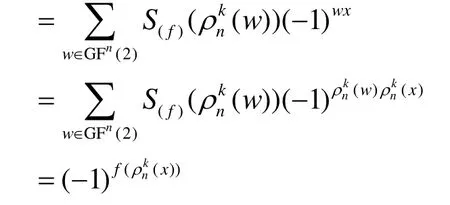
綜合1)、2)可知定理1成立。

定理 1說明n元k-階旋轉(zhuǎn)對稱函數(shù) Walsh譜S(f)(w )的取值個數(shù)不超過 gn,k個，約是n元旋轉(zhuǎn)對稱函數(shù)Walsh譜取值個數(shù)的k倍。所以它可以具有比n元旋轉(zhuǎn)對稱函數(shù)更為均勻的譜值分布，即更高的非線性度。

定理2 假設(shè)1≤k≤n,k|n，布爾函數(shù)f是n元k-階旋轉(zhuǎn)對稱函數(shù)，則其自相關(guān)函數(shù) rf(s)滿足

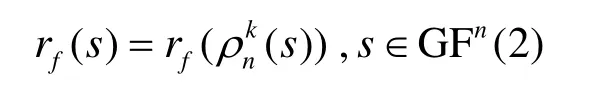
證明 由布爾函數(shù)Walsh譜和自相關(guān)函數(shù)的關(guān)系可知

又由定理1的結(jié)論知

定理2的逆命題是不成立的（Bent函數(shù)的自相關(guān)函數(shù)在所有非零點都是零，但Bent函數(shù)顯然不全是k-階旋轉(zhuǎn)對稱函數(shù)）。所以定理2不能作為k-階旋轉(zhuǎn)對稱函數(shù)的等價判別條件。

3.2 k-階旋轉(zhuǎn)對稱函數(shù)軌道中的長圈與短圈計數(shù)

由前述可知，k-階旋轉(zhuǎn)對稱函數(shù)的輸出序列、Walsh譜和自相關(guān)函數(shù)等都可以通過其軌道進行分類，所以有關(guān)k-階旋轉(zhuǎn)對稱函數(shù)的軌道的計數(shù)和性質(zhì)的研究是有意義的。本節(jié)利用組合論的知識分別給出了k-階旋轉(zhuǎn)對稱函數(shù)的軌道中的長圈和短圈的計數(shù)公式。首先介紹幾個基本概念。

引理2[2](Burnside引理) 假設(shè)G為一個作用在集合S上的置換群，則G作用在S上得到的軌道數(shù)量為，其中

引理 3[10](容斥原理) 設(shè) A1, A2,… ,An是有限集合，則

文獻[8]根據(jù)g 引理2給出了下面結(jié)論。

定理3[8]n,k表示n元k-階旋轉(zhuǎn)對稱函數(shù)的軌道的個數(shù)，則，φ(t)為歐拉函數(shù)

表1給出當(dāng) n = 4 ,6,… ,1 5時， gn,k的取值。

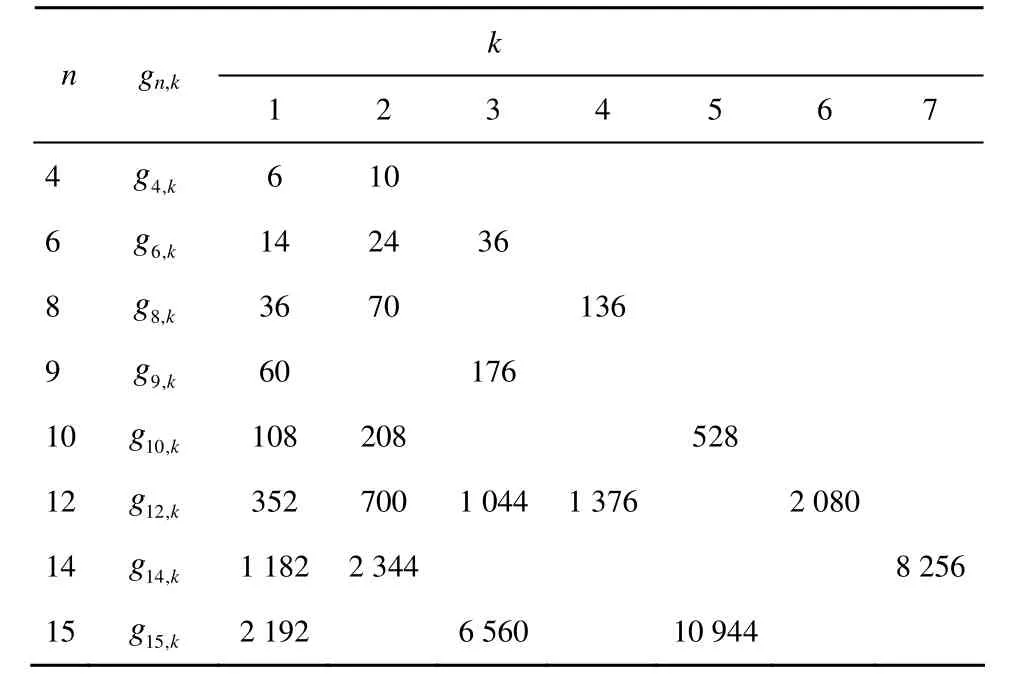
表1 n=4,6,…,15時gn,k的取值

通過表1可以看出，k-階旋轉(zhuǎn)對稱函數(shù)的軌道個數(shù)約是旋轉(zhuǎn)對稱函數(shù)的軌道個數(shù)的k倍。

推論1 對于素數(shù)p，若 n = pa，顯然 k = pb且0≤b≤a，則

證明 因為 n = pa,k =pb，其中，0≤b≤a。則可用 pi,0≤ i≤ a - b表示所有的因子，又因為φ( t ) 為歐拉函數(shù)，則由歐拉函數(shù)的性質(zhì)得φ( t) = φ ( pi) = pi- pi-1。由定理1可知：

定理 4 hn,k表示n元k-階旋轉(zhuǎn)對稱函數(shù)的軌道所有長圈的個數(shù)，則，μ(d)為默比烏斯函數(shù)

證 明 首 先 對 于 給 定 的1 ≤ k ≤ n ,k|n ， 令，易知G是循環(huán)群，對任意的π∈G，π可以分解成兩兩不相交且長度相同的輪換之積。令，表示在G作用下由向量x生成的軌道，定義軌道的重量為向量x的漢明重量。

i0或1。因此，。又對任意的? { p1, p2,… pl}，可知 l cm( pj1, pj2,… , pjs)=pj1，所以。由引理3可知：

又因為每個長圈的元素個數(shù)都為n個，所以有：

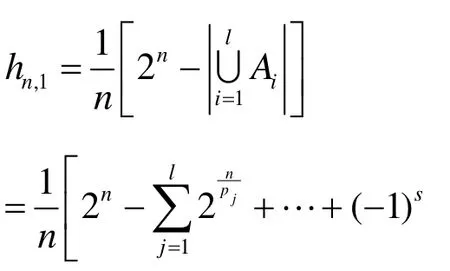
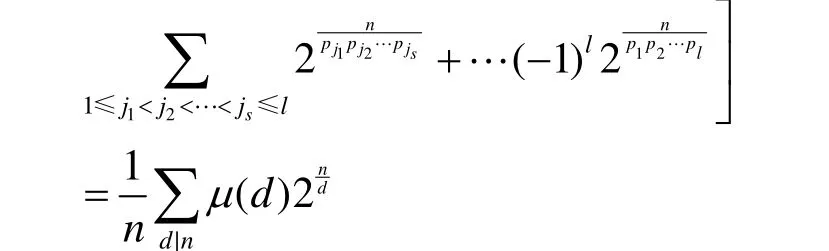
2) 當(dāng) k ＞ 1 時 ， 則 G = { ρk,ρ2k,… ,ρmk}。 令nnn。 對 任 意 的 x∈ G Fn(2)， 若，則存在i|m(i＜m)，使得。又因為：

為k個兩兩不相交的輪換之積，且每個輪換的長度為m。用fix來表示GFn(2)在 G {ρn}下保持不動n的點，由1)的結(jié)論可知：

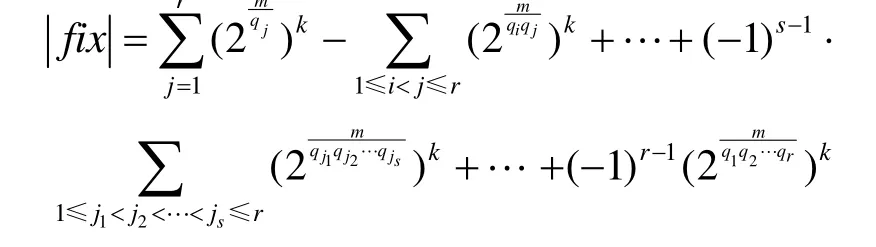
故

綜上所述，定理4的結(jié)論是成立的。表2給出當(dāng) n = 4 ,6,… ,1 5時 hn,k的取值。

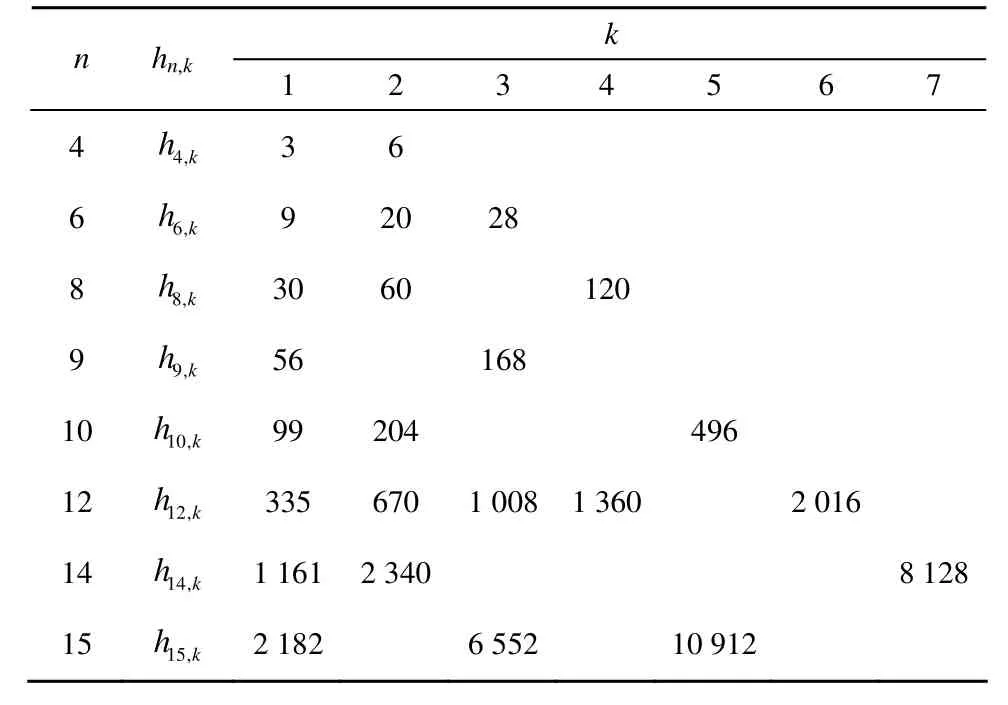
表2 n=4,6,…,15時hn,k的取值

對比表1可以發(fā)現(xiàn)，在k-階旋轉(zhuǎn)對稱函數(shù)的軌道中長圈占大多數(shù)。

推論 2 假設(shè) sn,k表示n元k-階旋轉(zhuǎn)對稱函數(shù)的軌道中所有短圈的個數(shù)，則

證明 因為 sn,k= gn,k- hn,k, 所以結(jié)論是顯然的。

前述結(jié)論在 k =1時即為旋轉(zhuǎn)對稱函數(shù)的軌道計數(shù)的結(jié)論，其相應(yīng)的結(jié)論Sarkar和Maitra在文獻[2]中已有詳細(xì)的描述。值得注意的是，文獻[3]所給出的旋轉(zhuǎn)對稱函數(shù)的軌道中的長圈的計數(shù)公式在n = pa1… pal為n的標(biāo)準(zhǔn)分解式時為1l

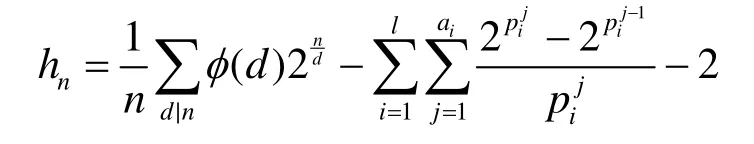
而本文定理4在 k = 1時為

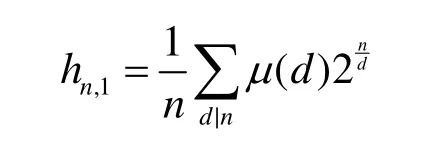
經(jīng)計算在 n = 1 2 = 22× 3 時文獻[2]的結(jié)論為h12= 3 44，而定理 4的結(jié)論為 h12,1= 3 35。經(jīng)驗證12元旋轉(zhuǎn)對稱函數(shù)的軌道中長圈個數(shù)為335個，說明文獻[2]的結(jié)論在 n = 1 2時是不成立的。

具體原因是，Sarkar和Maitra得出的n元旋轉(zhuǎn)對稱函數(shù)的軌道中所有短圈的數(shù)量為

之后將軌道總數(shù)減所有短圈的數(shù)量，所得即為n元旋轉(zhuǎn)對稱函數(shù)的軌道中所有長圈的數(shù)量。但是， sn只計算了所有在和作用下不動的短圈數(shù)量，而沒有計算所有在 ρnd作用下不動的短圈數(shù)量，其中

所以Sarkar和Maitra給出的旋轉(zhuǎn)對稱函數(shù)軌道中的長圈和短圈的計數(shù)公式在 n = pa1… pal,l=2且1l存在 ai≥ 2 (i = 1 ,2)或 l ≥ 3 時都是不正確的。

表3給出當(dāng)n=1,2,…,30時 hn與 hn,1的取值對比。

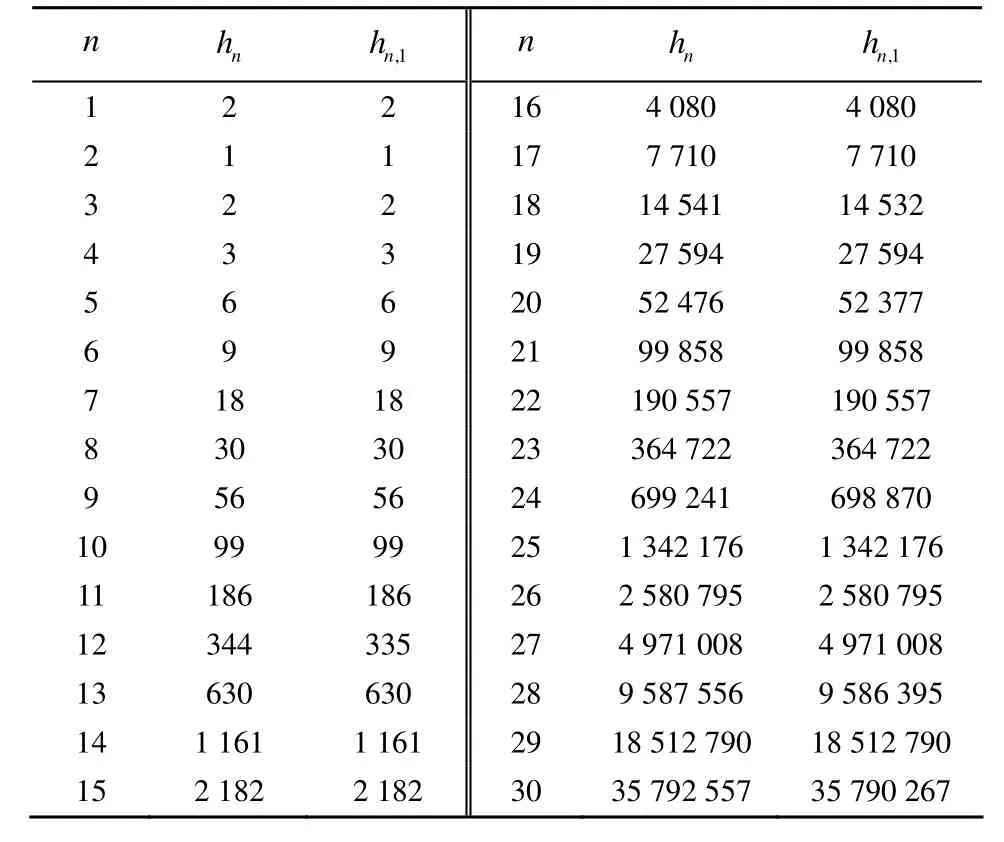
表3 n=1,2,…,30時hn與hn,1的取值對比

通過研究k-階旋轉(zhuǎn)對稱函數(shù)的軌道以及軌道中的長圈和短圈的計數(shù)，可以了解k-階旋轉(zhuǎn)對稱函數(shù)的軌道的性質(zhì)，從而為更為深入地研究k-階旋轉(zhuǎn)對稱函數(shù)的密碼學(xué)性質(zhì)提供幫助。

4 結(jié)束語

本文分析了k-階旋轉(zhuǎn)對稱函數(shù)的性質(zhì)，證明了k-階旋轉(zhuǎn)對稱函數(shù)的 Walsh譜和自相關(guān)函數(shù)滿足k-階的旋轉(zhuǎn)對稱。經(jīng)分析發(fā)現(xiàn)k-階旋轉(zhuǎn)對稱函數(shù)的很多性質(zhì)都可以利用其軌道來刻畫，并利用組合論的知識給出了n元k-階旋轉(zhuǎn)對稱函數(shù)軌道中的長圈和短圈的計數(shù)公式。目前，對于k-階旋轉(zhuǎn)對稱函數(shù)的研究工作才剛剛開始，通過深入研究這一類特殊的布爾函數(shù)函數(shù)從而尋找到密碼學(xué)性質(zhì)優(yōu)良的布爾函數(shù)，在理論和實踐上都具有重要的意義。

[1] PIEPRZYK J, QU C X. Fast hashing and rotation-symmetric functions[J]. Journal of Universal Computer Science, 1999, 5(1): 20-31.

[2] SARKAR P, MAITRA S. Rotation symmetric Boolean functions-count and cryptographic properties[J]. Discrete Applied Mathematics, 2008,156: 1567-1580.

[3] SARKAR P, MAITRA S, CLARK J. Results on rotation symmetric bent and correlation immune boolean functions[A]. Fast Software EncryptionFSE’ 2004[C]. Berlin, 2004. 161-177.

[4] KAVUT S, YüCEL M D. Search for boolean functions with excellent profiles in the rotation symmetric class[J]. IEEE Transactions on Information Theory, 2007, IT-53(5): 1743-1751.

[5] MAXIMOV A, HELL M, MAITRA S. Plateaued rotation symmetric boolean functions on odd number of variables[EB/OL]. http://eprint.iacr.org/2004/144.pdf.

[6] MAXIMOV A. Classes of plateaued rotation symmetric Boolean functions under transformation of Walsh spectra[EB/OL]. http:// eprint.iacr.org/2004/354.pdf.

[7] KAVUT S, SARKAR P, MAITRA S, et al. Enumeration of 9-variable rotation symmetric boolean function having nonlinearity>240[A].Cryptology-INDOCRYPT’ 2006[C]. Berlin, 2006.266-279.

[8] KAVUT S, YüCEL M D. Generalized rotation symmetric and dihedral symmetric Boolean functions-9 variable Boolean functions with nonlinearity 242[EB/OL]. http://eprint.iacr.org/2007/308.pdf.

[9] 李世取, 曾本勝, 劉文芬. 密碼學(xué)中的邏輯函數(shù)[M].北京：北京中軟電子出版社，2003.LI S Q,ZENG B S,LIU W F. Logic Functions in Cryptography[M].Beijing: Zhongruan Electric Publishing Company,2003.

[10] 盧開澄, 盧華明. 組合數(shù)學(xué)（第三版）[M]. 北京: 清華大學(xué)出版社,2002.LU K C,LU H M. Combinatorial Mathematics (Third Edition)[M].Beijing: Tsinghua University Press,2002.