基于多級混合單元模型的最小混相壓力計算方法

鞠 東 平

（中油遼河油田公司， 遼寧 盤錦 124109）

基于多級混合單元模型的最小混相壓力計算方法

鞠 東 平

（中油遼河油田公司， 遼寧 盤錦 124109）

最小混相壓力（MMP）是混相氣體注入工程設(shè)計的關(guān)鍵參數(shù)之一，在MMP下，驅(qū)替效率達到100%。在本研究中，提出了一個基于多級混合單元模型的新方法來識別關(guān)鍵結(jié)線，從而計算出最小混相壓力。多級混合單元模型是細管實驗中連續(xù)氣體注入過程中的一個離散模型。在該方法中，對于nc組分的體系，研究發(fā)現(xiàn)有nc+1個相同組成的區(qū)和nc-1個關(guān)鍵結(jié)線。隨著注入氣體批次數(shù)的增加，關(guān)鍵結(jié)線以反序的形式出現(xiàn)，如初始結(jié)線首先出現(xiàn)，注入結(jié)線最后出現(xiàn)。該研究結(jié)果有助于新方法識別所有的關(guān)鍵結(jié)線，因此特別適用于氣體注入的研究。本方法所預測的結(jié)果與細管實驗的結(jié)果和其他研究者的結(jié)果相對比是十分吻合。

多次接觸混相；最小混相壓力；多級混合單元模型；細管實驗；提高采收率

注入氣體是一個較有效的提高采收率方法之一，特別在氣體發(fā)生混相的情況下。混相驅(qū)是一個理想的驅(qū)替機理。當壓力高于最小混相壓力（MMP）時，注入氣體和原油之間經(jīng)過多次接觸達到混相。如果注入的氣體與原油之間發(fā)生混相，那么在驅(qū)替前緣的界面張力就變?yōu)榱悖瑫r束縛油滴的毛管力就會消失。因此，MMP是混相氣體注入工程設(shè)計的最重要的參數(shù)。

在文獻中，有不同種確定MMP的方法。Wang和 Orr【1】對這些方法進行了較為系統(tǒng)的闡述。在這些方法中，分析法和多級混合單元模型是最具吸引力，這是由于這2個方法可以將復雜的混相機理進行充分的解釋。Zick【2】研究結(jié)果表明，多級混合單元模型能夠被用于模擬冷凝和氣化同時存在的驅(qū)替過程。在提高采收率的過程中，存在許多復雜的體系，如聚合物，表面活性劑和鹽水。對于這些復雜的體系，準確地預測MMP顯得很重要的。因此,對這些復雜的體系 MMP的預測逐漸引起了人們的研究興趣。Zhao等【3】的研究結(jié)果認為，多級混合單元模型適合于三相或多相系統(tǒng) MMP的預測。到目前為止，分析法局限于具有任意組分的兩相系統(tǒng)，或氣/水/油三相系統(tǒng)【4,5】。在本研究中，首先選擇了多級混合單元模型來預測簡單油/水兩相系統(tǒng)的MMP，為多相系統(tǒng) MMP的預測研究打下初步的基礎(chǔ)。在本研究中，所使用的方法預測的結(jié)果與細管實驗的結(jié)果和其他研究者的結(jié)果相對比是十分吻合。

1 多級混合單元模型

在本文，一個多級混合單元模型被用于計算關(guān)鍵結(jié)線長度，然后預測MMP。多級混合單元模型就是一個細管實驗中連續(xù)氣體注入過程的離散模型。填充的細管被離散為一系列具有相同體積的單元，連續(xù)注入的氣體被離散為一系列具有相同體積的批次（如圖1所示）。假設(shè)條件為：每個單元的溫度和壓力是恒定的；單元間不存在物理擴散；每個單元和單元間不存在毛管力作用；每個單元中的混合是完全混合。這樣，多級混合單元模型就可以轉(zhuǎn)變成單純的熱動力P/T閃蒸計算。

圖 1 單元與單元模擬的示意圖Fig.1 Schematic diagram of cell-to-cell simulation

氣體的多次接觸混相是由一組nc– 1個關(guān)鍵結(jié)線控制：初始結(jié)線、注入結(jié)線和nc– 3個交叉結(jié)線[3，6-8]。初始結(jié)線是在組分空間中可以延長至代表原始油組分的點的平衡結(jié)線。注入結(jié)線是在組分空間中可以延長至代表注入氣組分的點的平衡結(jié)線。交叉結(jié)線是在雙結(jié)點面上的平衡結(jié)線。MMP被定義為使關(guān)鍵結(jié)線中任何一個成為臨界結(jié)線的最低壓力。有許多標準用來判斷MMP，但是，我們近期的研究結(jié)果表明：關(guān)鍵結(jié)線長度為零是最快捷、最精確的判斷 MMP的判據(jù)。因此，這個問題就轉(zhuǎn)為如何識別關(guān)鍵結(jié)線的問題。目前，唯一識別關(guān)鍵結(jié)線的方法是結(jié)線交叉法，也就是說，任何兩個相鄰的關(guān)鍵結(jié)線一定相交。通過解這組2nc(nc-1)個方程，所有的關(guān)鍵結(jié)線就可以被找到。但是，在解方程的過程中，關(guān)鍵問題是初值猜測的確定和解的非唯一性。

由于通過多級混合單元模型可以找到所有的關(guān)鍵結(jié)線，所以，基于結(jié)線長度的確定可以預測MMP。結(jié)線長度定義為：

其中，xi和yi分別是i組分的液相和氣相平衡摩爾分數(shù)。在 MMP下，所有關(guān)鍵結(jié)線中的任何一個結(jié)線的長度變?yōu)?。

在細管實驗中氣體驅(qū)替過程的計算步驟總結(jié)如下：

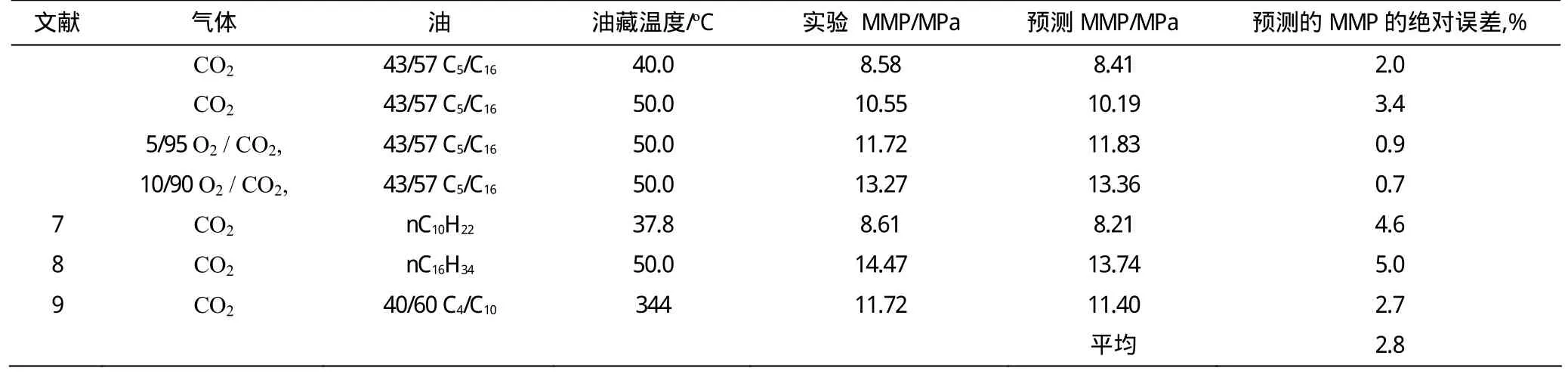
第1步：程序模擬一定數(shù)量的連成一串、相同體積的單元。所有的單元初始飽和相同的流體（原油）。一定量的氣體加入第1個單元。注入氣體和單元中的流體混合后，假定為是充分混合，通過 P/T閃蒸計算可以確定單元中的氣相分數(shù)(v)。如果v31，混合物處于或高于其露點上，所有的氣體體積一定是比單元的體積大。那么，多余氣體就由第一個單元移到第2個單元。如果v￡ 0，混合物處于或低于其泡點下。那么，多余油就由第一個單元移到第二個單元。如果0

其中，Vl和Vv分別為閃蒸計算后液相和氣相的體積。

第2步：在第二單元形成的多余體積移到第三單元，如此類推，直到從最后單元采出來。當一個氣體批次的計算完成后，一個新的氣體注入開始，一個一個單元的傳輸計算重復開始。如果在當前壓力下找到所有的關(guān)鍵結(jié)線后，就進行下一個壓力的計算。

2 結(jié)果與討論

對于所有的計算，純組分的臨界數(shù)據(jù)和離心因子是恒定不變的【9】。模型的參數(shù)和所使用的二元交互作用參數(shù)如表1和表2所示。選擇的單元總數(shù)應(yīng)該確保注氣過程穩(wěn)態(tài)組成路徑的達到。單元的體積，VGOR，和分流函數(shù)不影響關(guān)鍵結(jié)線的確定，因此，這些參數(shù)不影響 MMP的計算。注入氣的總批次數(shù)由式（4）計算得到：

其中，對于細管實驗油的采收率計算，所要求的注入氣體量是1.2倍孔隙體積。

2.1 文獻中的結(jié)果

在下面的討論中，使用了一些文獻中的體系來驗證本文算法的準確性。

本研究選的4組分體系是：氣體混合物（50%CH4+ 50% N2）和油（50% CH4, 16.24% C4H10, and 33.76% C10H22）。Jessen 等【10】已經(jīng)很好地研究過這個體系。其組分的性質(zhì)和PR狀態(tài)方程的二元交互作用參數(shù)列于表1。

表1 二元交互作用參數(shù)Table 1 Binary interaction parameters

表2 多級混合模型的參數(shù)Table 2 Parameters of the multiple-mixing-cell model

結(jié)線長度的計算結(jié)果如圖2所示。對于這個4組分體系，有3個關(guān)鍵結(jié)線（初始結(jié)線，交叉結(jié)線和注入結(jié)線）。在MMP下，初始結(jié)線長度變?yōu)榱恪Ｈ鐦俗⑺荆嬎阍趬毫咏麺MP是停止；在MMP下，初始結(jié)線的長度一定為零。這是一個在臨界區(qū)進行閃蒸計算普遍遇到的難題。通過外推法，預測的MMP是31.5 MPa. 這個值與文獻值(31.3 MPa)是十分接近。初始油結(jié)線確定了這個 4組分體系的MMP。這個結(jié)果表明了這個體系的驅(qū)替機理是氣化驅(qū)替。同時，計算了另外2種注入氣的MMP。其中一種氣體混合物是90% CH4+ 10% N2，另外一種氣體混合物是75% CH4+ 25% N2。預測的MMP也與文獻值【10】十分吻合（如圖3和圖4）。

圖2 注入氣體為50%N2 和 50%CH4的模擬計算的關(guān)鍵結(jié)線長度Fig.2 Key tie-line lengths of four components in the simulation of a 50/50 mixture of N2 and CH4

在本研究中，也使用文獻中的細管實驗數(shù)據(jù)來檢驗我們的算法的準確性（表3列出了在本研究中使用的文獻數(shù)據(jù)）。可以發(fā)現(xiàn)，作者的算法與文獻的細管實驗的結(jié)果是十分吻合。作者的算法最大可以產(chǎn)生5.0%的相對誤差和2.8%的平均誤差。從表3可以看出，作者的算法具有較好的預測精度。

圖3 注入25% N2 和 75% CH4的模擬計算關(guān)鍵結(jié)線長度Fig.3 Key tie-line lengths in the simulation of a 25/75 mixture of N2 and CH4

圖4 注入90% N2 和 10% CH4的模擬計算關(guān)鍵結(jié)線長度Fig.4 Key tie-line lengths in the simulation of a 90/10 mixture of N2 and CH4 as the injection gas

2.2 細管實驗結(jié)果

由于文獻中的 CO2和 C16H34的kij值是不一致的，在本研究工作中，擬合了這個參數(shù)，并預測了在溫度為50oC的模擬油與純CO2的MMP。同時，也預測了模擬油與含有 O2的 CO2的 MMP。如表 1所示，設(shè)涉及O2的kij為零。

表3總結(jié)了預測結(jié)果。可以看出，預測的結(jié)果在實驗誤差范圍內(nèi)是值得信賴的。預測的結(jié)果也表明CO2中的O2存在使MMP增加。預測的在溫度40oC和50oC下的模擬油與純CO2的MMP與實驗結(jié)果是十分吻合。對于模擬油，隨著溫度的增加，MMP增加。

表3 合成油MMP實驗結(jié)果與預測結(jié)果的對比Table 3 Comparison of measured and calculated MMP

圖5是O2對MMP的影響。下面的討論中，使用了一些文獻中的體系來驗證本文算法的準確性。

圖5 在溫度50 oC 下含 O2的CO2對 MMP 的影響Fig.5 The MMP for model oils with O2-contaminated CO2 gases at 50 oC

3 結(jié) 論

通過上面的結(jié)果和討論，可以歸納下面的結(jié)論：

(1) 多級混合單元模型是一個確定氣驅(qū)過程中所有關(guān)鍵結(jié)線的有活力的方法；

(2) 本算法預測的結(jié)果與細管實驗結(jié)果及文獻結(jié)果是十分吻合。

［1］ Wang Y, Orr Jr FM. Calculation of Minimum Miscibility Pressure[C].SPE 39683, 1998：1-10.

［2］Zick A A. A Combined Condensing/Vaporizing Mechanism in the Displacement of Oil by Enriched gases[C], SPE 15493, 1986： 1-11.

［3］ Zhao G B, Adidharma H, Towler B, Radosz M. Using a Multiple-Mixing-Cell Model to Study Minimum Miscibility Pressure Controlled by Thermodynamic Equilibrium Tie lines[J]. Industrial &Engineering Chemistry Research. 2006,45(23)：7913-7923.

［4］ LaForce T C, Jessen K, Orr Jr F M. Analytical Solutions to Three-Phase Four-Component Displacements[C]. SPE 102777,2006：1-13.

［5］ Wang Y, Orr F M Jr. Analytical calculation of minimum miscibility pressure[J]. Fluid Phase Equilibria, 1997, 139 (1-2)： 101-124.

［6］ Jaubert J –N,Arras L, Neau E, Avaullee L. Properly Defining the Classical Vaporizing and Condensing Mechanisms When a Gas Is Injected into a Crude Oil[J]. Industrial & Engineering Chemistry Research, 1998, 37 (12)： 4860-4869.

［7］ Orr F M Jr, Dindoruk B, Johns R T. Theory of Multicomponent Gas/Oil Displacements[J]. Industrial & Engineering Chemistry Research, 1995,34： 2661-2669.

［8］ Johns RT, Dindoruk B, Orr F M. Analytical theory of combined condensing/vaporizing gas drives[J]. SPE Adv. Tech. Ser., 1993,1( 2)：7-16.

［9］ Danesh A. PVT and Phase Behaviour of Petroleum Reservoir Fluids[M]. New York：Elsevier Science B.V, 1998.

［10］Jessen K, Stenby E H, Orr Jr F M. Interplay of Phase Behavior and Numerical Dispersion in Finite-Difference Compositional Simulation[J]. SPE Journal, 2004： 193-201.

A New Approach for Calculation of Minimum Miscibility Pressure Based on a Multiple-Mixing-Cell Model

JU Dong-ping
（China National Petroleum Corporation Liaohe Oilfield Company, Liaoning Panjin 124109, China）

A key parameter in the design of the miscible gas injection process is the minimum miscibility pressure(MMP), at which the local displacement efficiency approaches 100%. In this paper, a new approach based on the multiple-mixing-cell model has been proposed to identify the key tie lines, and therefore to calculate the MMP. The multiple-mixing-cell model is a discrete model of the continuous gas injection process in the slim tube experiment. In this approach, fornccomponents, it’s found that there arenc+1 constant-composition zones andnc-1 key tie lines.Upon increasing the batch number of the injected gas, these key tie lines appear in a reverse order, i.e., the initial tie line appears first and the injection tie line appears last. This finding leads to a new approach to identifying the key tie lines. This approach provides a unique solution to find all the key tie lines and is therefore particularly suitable for gas injection studies. Predicted results from the proposed approach are shown to be in excellent agreement with slim tube data and other slim tube simulators presented in the literature.

Multicontact miscibility; Minimum miscibility pressure; Multiple-mixing-cell model; Slim tube experiment; Enhanced oil recovery

TQ 018

A

1671-0460（2012）01-0091-04

2011-00-00

鞠東平（1970-），女，遼寧盤錦人，工程師，1992年畢業(yè)于大慶石油學院采油工程專業(yè)，研究方向：油氣田開發(fā)工作。E-mail：fengyi.wu@163.com。