推力轉向噴流與高速主流干擾參數影響規律的數值模擬研究

司芳芳，袁先旭，李建強，陳 琦

（中國空氣動力研究與發展中心，四川 綿陽 621000）

0 引 言

新一代戰斗機要求具有良好的機動性和短距離起降性能。在進行大迎角機動飛行時，飛機繞流現象復雜，流動分離嚴重，垂尾等操縱面浸沒在尾跡流動之中，操縱面效率急劇降低甚至完全失效，通過操縱面偏轉獲得所需控制力和力矩的方法，已經很難滿足大迎角機動的要求，必須采用推力矢量控制技術。推力矢量技術作為第四代戰斗機設計的一項關鍵技術，從上個世紀八十年代開始，美國就開展了廣泛的研究，包括理論與計算分析、縮比模型試驗、飛行模擬器仿真和飛行演示驗證等多種手段，并已成功應用于F－22、F－35等第四代主力戰機中。

現代戰斗機的大后掠角、尖前緣的機翼氣動布局在較大迎角下會產生前緣渦，在加裝推力轉向噴管后，矢量噴流的引射作用，使前緣渦的位置向內和向下移動，即向機身方向移動；再加上渦對的誘導作用，會減少機翼后緣的逆壓梯度，使前緣渦渦核軸向速度增加，前緣渦旋緊，渦強增強，對翼面流動的誘導能力增強；在破裂渦流動狀態，矢量噴流對主流影響最大，可能使前緣破裂渦恢復，從而引起超環量效應。在實際飛行中，推力轉向尾噴流和主流之間，特別是在飛行攻角較大或來流馬赫數較高時，噴流和外流之間產生強干擾，從而形成復雜的渦系，波系和分離流，同時改變了噴管內流狀態，使激波、分離波系產生位置發生變化，并使機身壓力分布發生變化，影響飛機的整體氣動特性。我們知道，后機身流場是縱向力矩系數的主要影響因素，它對噴管內流壓力變化很敏感，因此，必須考慮矢量噴管推力及控制力矩對整個機身的壓力分布的影響，將矢量噴管與飛機外形的氣動布局型式結合起來研究，以提高矢量噴管的推力效率及飛機性能。值得注意的是，推力矢量尾噴流干擾效應與傳統噴管的噴流干擾效應是相當不同的［1］，傳統噴管的噴流干擾效應是一種局部的弱擾動，僅集中在噴管出口附近的區域；而推力矢量尾噴流干擾效應則是一種強擾動，對戰斗機的整體氣動特性有相當大的影響，這種影響并強烈依賴于機身／推進系統的集成設計，如F－22戰斗機就細致設計了雙發噴管的間距（小間距設計），并通過加長尾錐來隔離雙發噴流的干擾。無疑，研究主流與推力矢量尾噴流的干擾效應規律和機理將是機身／推進系統優化集成設計的基礎。

為此，針對推力轉向噴管開展尾噴流／主流干擾對全機氣動特性影響研究，具有較高的學術價值和重要的應用價值，可為推力矢量技術的工程應用乃至先進飛行器的研制奠定技術基礎。

1 計算方法

當戰斗機利用推力矢量技術進行大迎角過失速機動時，推力轉向噴流與高速主流干擾流場極為復雜，真實的物理過程包括大范圍湍流分離流、多相流、高低溫氣體摻混流動、內外流干擾、激波／膨脹波／剪切層／旋渦干擾等。要想完全真實模擬，對數值計算模型和計算方法有很高的要求。這里與擬開展的高速風洞試驗研究相同，采用了冷噴模擬方法，對數值模擬方法的要求主要是精細的網格、高精度的計算格式和適用的湍流模型。

1.1 數值方法

控制方程為可壓縮的N－S方程。空間離散采用Steger－warming通量差分，采用 minmod限制器，MUSCL插值采用二階插值，時間離散采用LU－SGS方法。鑒于目前DNS、LES和RANS存在的問題，本文選用課題組自主研發的一種基于分區混合和基于湍流尺度混合的雙重RANS／LES混合模型，該模型經過典型算例的驗證，計算結果均與試驗和文獻計算結果符合較好，表明該RANS／LES混合模型能給出較合理的湍流宏觀平均量，值得探索用于推力轉向噴流與高速主流干擾效應的數值模擬研究的實際工程問題中。方法細節可參見文獻［2］。

1.2 邊界條件

遠場采用無反射邊界條件；壁面采用無滑移、絕熱壁邊界條件；計算需要進行全流場計算，對稱子午面為塊邊界，采用一一對接邊界條件。可以證明，上述邊界條件處理方法不引入非對稱誤差。矢量噴管出口設為噴流入口邊界，給定參數有噴流的壓強pj，密度ρj，速度Vj和噴流偏轉角δj。入口邊界條件是由已知的噴流總壓Ptj、總溫Ttj和噴流馬赫數Mj按一維等熵流公式計算得到：

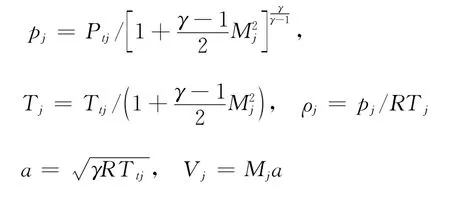
本文使用的噴流入口條件，未考慮矢量噴管內流與主流干擾情況，并不符合實際噴流情況。實際情況下，外流將影響噴管內流場的建立，下一步將對噴管內流和主流的干擾進行深一步研究。

1.3 計算模型和網格

首先依據圖紙，生成本文的計算用數模，按計劃分別計算了矢量噴管無偏轉（δj＝0°）、向下偏轉10°（δj＝－10°）、向下偏轉20°（δj＝－20°）和向下偏轉30°（δj＝－30°）的情況。

在進行數值模擬時，首先要盡量減小網格對計算結果的影響。為了保證計算的精度和效率，采用結構化網格生成技術，由于研究對象幾何形體的復雜性，采用了多塊搭接網格，且只計算半流場。為準確模擬噴流干擾區的尺度，應保證足夠的干擾區附近流向的網格密度，所以在模型的頭部、翼尖、壁面和尾部噴口附近局部加密。圖1為噴管偏轉不同角度時網格的空間分布，網格數量都約為709.19萬，在空間分為6塊，上游距飛機頭部3.0L，下游距尾噴管4.0L，遠場邊界距中心線3.0L。

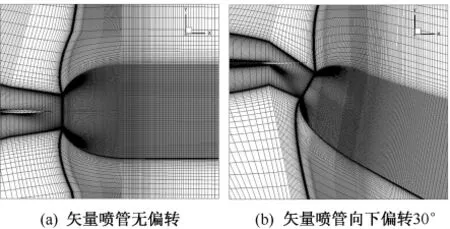
圖1 局部放大的計算網格Fig.1 The computation grid with local zoom

1.4 計算條件

噴流對全機氣動干擾是由內、外流的相互作用所引起的。通常情況下，噴流與主流氣體的理化特性并不完全相同，噴流介質的組分、分子量、化學反應和熱力學特性等因素都會對干擾流場的動力學和熱力學輸運特性及內、外流摻混過程產生影響，使流動復雜化。為了與后續風洞試驗研究保持一致，本文從噴流、主流均為完全氣體的簡單情況入手，數值模擬推力轉向尾噴流與高速主流干擾的復雜流場。主流和尾噴流條件的主要參數見表1，主流條件由標準大氣表計算。

表1 主流、噴流計算條件Table 1 The computation condition of main flow and jet flow

2 計算結果和分析

2.1 來流馬赫數影響

以攻角為15°，噴口總壓為300kPa，噴口總溫為300K，噴流馬赫數為1.0為例，對不同來流馬赫數的計算結果進行對比和分析。

圖2（a～f）分別給出了不同來流馬赫數時馬赫數等值線分布，從圖中可以看出，本文計算結果顯示了非常清晰的流場，刻畫出了噴口附近復雜的波系結構。可以得出如下結論：

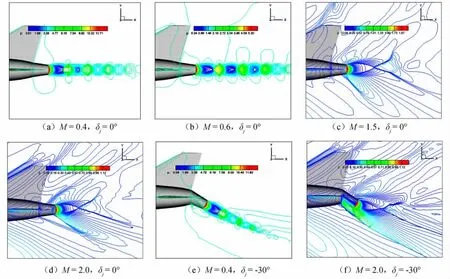
圖2 馬赫數等值線Fig.2 Mach number contours

（1）隨來流馬赫數數增大，主流與尾噴流干擾效應明顯增強。M＝0.4、δj＝0°時，主流雖有15°攻角，但對尾噴流幾乎沒有影響，壓力標識的噴流尾跡幾乎成一條直線向后傳播，清晰尾跡區達約全機長的一半；M＝0.6的情況與 M＝0.4基本相似；M＝1.5時，情況則有明顯變化，主流遭遇尾噴流膨脹波包，迎風側緊臨噴管出口截面，產生一道斜激波，導致噴流尾跡向上傾斜，實際推力矢量角發生損失；隨著主流M進一步增大，這一現象愈發明顯。造成這一現象的主要原因在于隨M增大，主流動壓增大，對噴流尾跡吹拂能力加強。

（2）隨來流M數增大，噴流波系結構發生明顯變化。M＝0.4時，噴流出口膨脹后形成馬赫盤（從二維對稱面來看，為正激波），隨M增大，馬赫盤不斷縮小，到M＝1.5時，幾為斜激波相交的魚尾波系形態。隨著M進一步增大，斜激波相交的魚尾波系形態愈發明顯。造成這一現象的主要原因在于隨M增大，噴管出口環境壓力降低，噴流出口后的繼續膨脹增強。

（3）當δj增大時，噴流干擾流場結構與噴流／主流干擾效應隨M的變化規律與δj＝0°的情況基本一致。但當δj＞0°后，基于現模型設計方案，噴管與機身之間的彎折角對主流有明顯影響，特別是當M＞1后，此處產生一道強壓縮激波，明顯改變主流和噴流的流場結構。但實際情況下，噴管偏轉時不可能有這樣明顯的彎折角，模型設計的失真有何影響，需進一步深入研究。

圖3（a～e）給出了δj＝0°、δj＝－20°、δj＝－30°時飛機氣動力系數隨來流馬赫數的變化，圖3（f）給出了δj＝0°、δj＝－10°、δj＝－30°時推力矢量角損失隨來流馬赫數的變化。可以看到：

（1）推力矢量噴管偏轉不同角度時，對升力系數和法向力系數影響很小，對軸向力和俯仰力矩的影響稍大。表明在高速主流條件下，攻角不大時，推力轉向噴流對主流的干擾局限于尾部局部區域，不明顯。這與文獻中低速推力矢量試驗研究的結論一致。

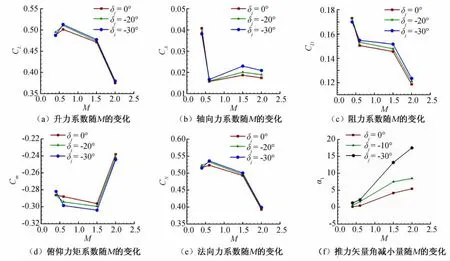
圖3 氣動力系數隨M變化Fig.3 Aerodynamic coefficient variation with M

（2）推力矢量角損失量隨噴管偏轉角度的增大而增大，隨來流馬赫數的增大而急劇增大。當來流馬赫數為0.4和0.6時，推力矢量角的損失較小，表明推力轉向控制效率很高。但當來流馬赫數超過聲速時，推力矢量角損失嚴重，在 M＝2.0、δj＝－30°情況，推力矢量角損失最大接近18°，表明此時噴管雖下偏30°，但實際俯仰方向的推力矢量只有下偏12°，效率很低。這說明推力矢量技術有一定的適用范圍，超過某個臨界M后，推力矢量技術代價較高，效率降低。

2.2 飛行攻角影響

顯而易見，飛行攻角也是一個重要的主流影響參數。實際上，推力矢量技術的一個重要考核即在大攻角操縱面效率降低時提供操縱力矩。這里，以噴口總壓為300kPa，噴口總溫為300K，噴流馬赫數為1.0為例，對來流馬赫數為0.6時飛行攻角在－10°～40°之間和來流馬赫數為2.0時飛行攻角在－10°～15°之間時的計算結果進行對比。

圖4（a～f）、圖5（a～c）給出了不同條件下用壓強著色的空間流線圖。通過對主翼背風渦流形態的比較分析，可以認為：

（1）M＝0.6、無噴流時，隨攻角增大，背風集中渦逐漸增強，低壓區范圍逐漸覆蓋幾乎整個上翼面，當攻角達40°，背風集中渦破裂，上翼面為破裂后的隨機尾跡流動覆蓋，流線壓力也明顯升高。這一演化過程符合眾所周知的三角翼背風渦流演化規律，表明本文基本流場計算是可靠的。

（2）對比δj＝0°和δj＝－20°與無噴流時的流場結構，攻角為20°和30°情況下，三者并無明顯區別，表明在中等攻角下，主翼上表面背風集中渦較強，此時，尾噴流對主流的干擾（引射效應）較弱。當攻角為40°時，情況則明顯不同，無噴流時主翼上表面背風集中渦已破裂，無明顯集中渦形態和低壓區，但有噴流時，機翼上流動又恢復出現明顯集中渦形態和低壓區（有噴流流場是以無噴流流場為初場繼續計算得到），表明在40°攻角情況下，推力轉向噴流的后緣引射效應比較明顯，使得已破裂的背風集中渦恢復，在外形上呈現出超環量效應。文獻中低速風洞試驗研究表明在低速大攻角情況下，推力轉向噴流的引射效應可使破裂的主翼集中渦重新恢復成集中渦形態，誘導出超環量效應，對全機氣動特性影響很大。但從圖6可以看出，攻角對氣動力系數的影響較小，這說明對于該簡化模型，在高速主流情況下，推力轉向噴流的影響相對較小，從定量上不足以說明產生了超環量效應。可能原因是簡化模型的主翼比較靠前，尾噴流對其影響較小；或主流M較高時，推力轉向噴流的影響減弱。

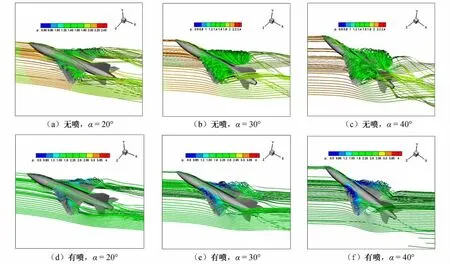
圖4 δj＝0°，M＝0.6時用壓強著色的流線圖Fig.4 Streamlines colored by pressure forδj＝0°，M＝0.6

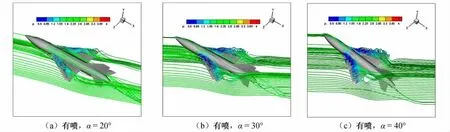
圖5 δj＝－20°，M＝0.6時用壓強著色的流線圖Fig.5 Streamlines colored by pressure forδj＝－20°，M＝0.6

圖6（a～e）分別給出了M＝0.6和M＝2.0在推力轉向噴流影響下的氣動力系數隨攻角的變化。圖6（f）給出了M＝0.6和M＝2.0時推力矢量角損失隨攻角的變化。

經分析，可得出以下結論：

（1）推力轉向噴流對軸向力的影響較大，這與軸向力系數的積分方式有關，這里在無噴流情況下，將噴管側面和底部都進行了積分，與試驗天平受力不一致。但不同噴流偏轉角有相互之間的比較意義。M＝0.6時，在攻角大于20°以后，不同噴流偏轉角對氣動力特性的影響才比較明顯，這與上面的流場結構分析基本一致。M＝2.0時，不同噴流偏轉角導致的尾部激波形態與強度明顯不同，因而在計算的攻角范圍內，噴流偏轉角對軸向力系數都有明顯影響，并隨攻角增大而增大，但對其他氣動力分量則幾乎沒有影響，表明超聲速情況下，噴流與主流干擾局限在尾部局部區域，沒有亞聲速條件下出現的超環量效應。究其機理，這與超聲速情況下，機翼的流動形態是相關的，M＝2.0時，三角翼背風區并無明顯集中渦形態，也與擾動在超聲速條件下只向后傳播有關。

（2）推力矢量角損失隨攻角增大而增大，除此以外，也與矢量噴管偏轉角、來流主流M 高度相關，推力矢量噴管偏轉角越大、來流馬赫數越高，推力矢量角的損失就越大，即實際推力矢量角與原推力矢量角的差別越大。但推力矢量角的損失程度在M＝0.6與M＝2.0時差別極為顯著，M＝0.6時，推力矢量角總的來說損失不大，在計算范圍內最大不超過4°，但M＝2.0時，推力矢量角損失相當大，最大可達18°，再次驗證了在超聲速條件下使用推力矢量技術代價高，實際上不可行。

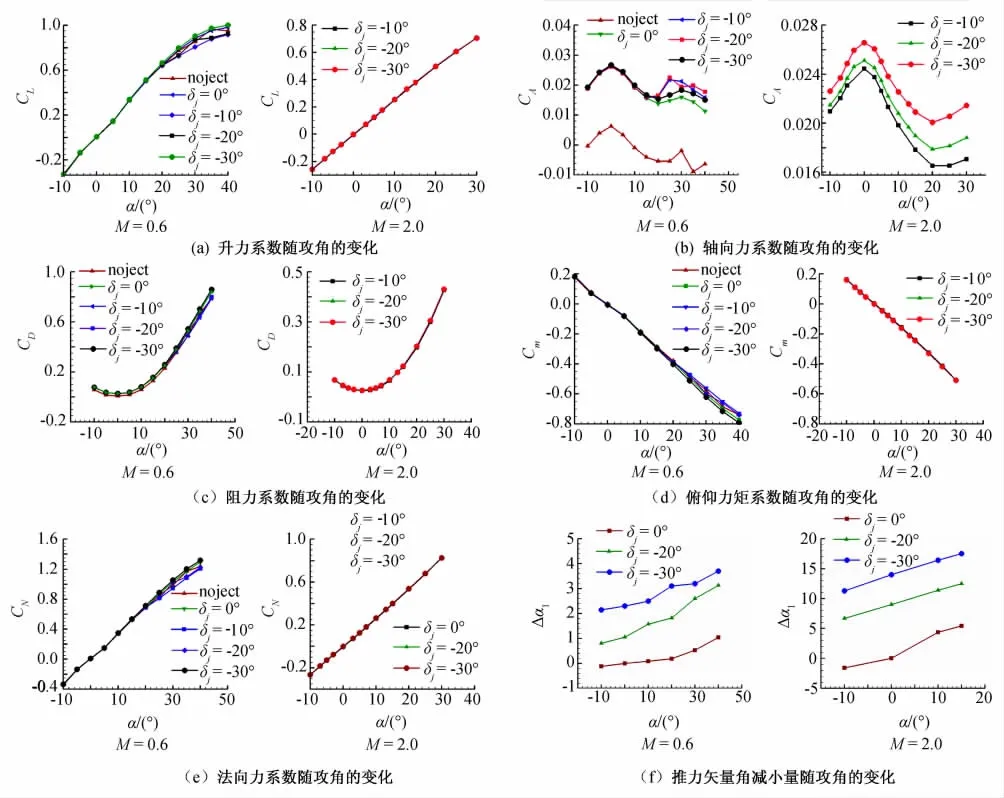
圖6 氣動力系數隨α變化Fig.6 Aerodynamic coefficient variation withα

2.3 噴流總壓

為考察噴流總壓的影響，以來流馬赫數為0.6和2.0，攻角為15°，噴口總溫為300K，噴流馬赫數為1.0為例，比較和分析噴口總壓分別取300kPa、400kPa、500kPa時對飛機氣動力系數的影響。

圖7（a～d）分別給出了噴口總壓分別取400kPa和500kPa時流場的馬赫數等值線分布。圖8分別給出來流馬赫數為0.6和2.0，δj＝0°，－10°，－20°，－30°時，氣動力系數隨噴流總壓的變化。總的來看，可有如下結論：

（1）噴流總壓對尾噴流流場結構有所影響，但并不改變流場結構的拓撲形態，只是強度有所不同。噴流總壓增大時，由于噴流馬赫數固定，則噴管出口靜壓增大，噴流出噴口后，進一步膨脹的能力加強，即噴流的穿透力增強。因此，M＝0.6時，總壓增大，噴流馬赫盤增大；M＝2.0時，總壓增大，斜激波相交點后移。

（2）由于總壓對流場結構沒有明顯改變，因此，總壓變化對全機氣動力特性的影響甚小，幾乎可忽略不計。

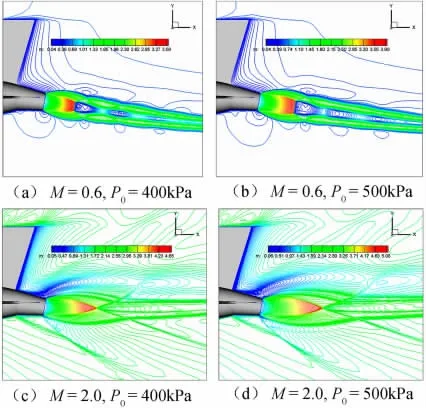
圖7 δj＝－10°時馬赫數等值線分布圖Fig.7 Mach number contours forδj＝－10°

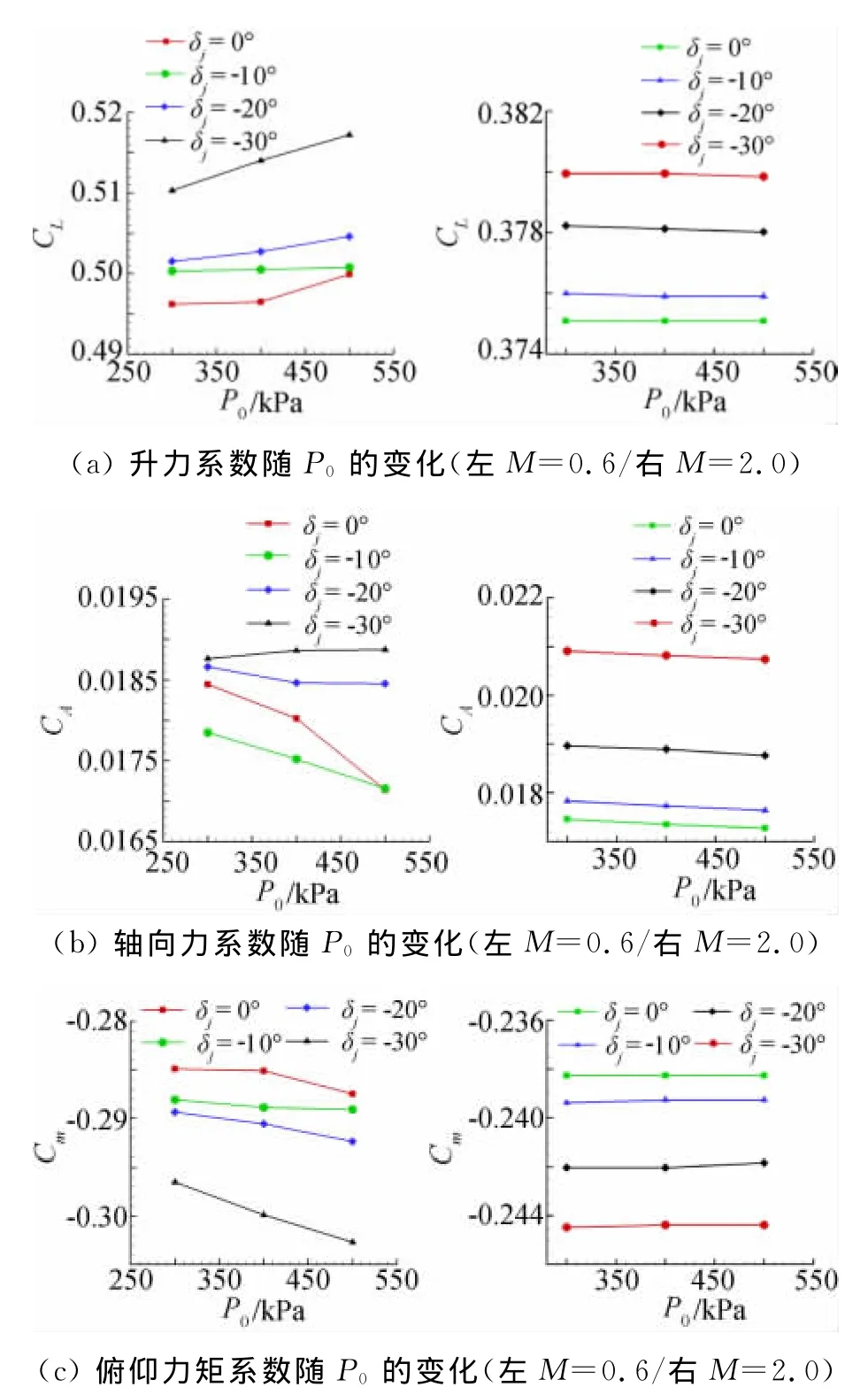
圖8 氣動力系數隨P0變化Fig.8 Aerodynamic coefficient variation with P0

2.4 噴流馬赫數

為考察噴流馬赫數的影響，以來流馬赫數為0.6和2.0，攻角為15°，噴口總壓為300kPa，噴口總溫為300K為例，比較噴流馬赫數在1.0～2.8之間取值時對飛機氣動力系數的影響。

圖9（a～d）分別給出了噴流馬赫數為1.2和2.0時流場的馬赫數等值線分布。圖10分別給出了來流馬赫數為0.6和2.0，δj＝0°，－10°，－20°時，氣動力系數隨噴流馬赫數的變化。總的來看，可有如下結論：

（1）噴流馬赫數對尾噴流流場結構有明顯影響，甚至改變流場結構的拓撲形態。噴流馬赫數增大時，由于噴流總壓固定，則噴管出口靜壓減小，噴流出噴口后，進一步膨脹的能力減弱，即噴流的穿透力減弱。因此，M＝0.6時，噴流馬赫數增大，噴流馬赫盤減小，Mj＝1.2時，馬赫盤即已消失，成為斜激波相交形態，Mj進一步增大，則斜激波相交點前移；M＝2.0時，噴流馬赫數增大，斜激波相交點前移。

（2）噴流馬赫數雖對流場結構有明顯改變，但局限于噴管以后的噴流尾跡區域，因此，噴流馬赫數變化對全機氣動力特性的影響甚小，幾乎可忽略不計。

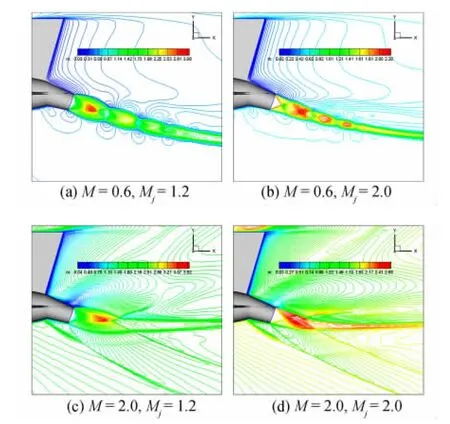
圖9 δj＝－20°時馬赫數等值線分布圖Fig.9 Mach number contours forδj＝－20°

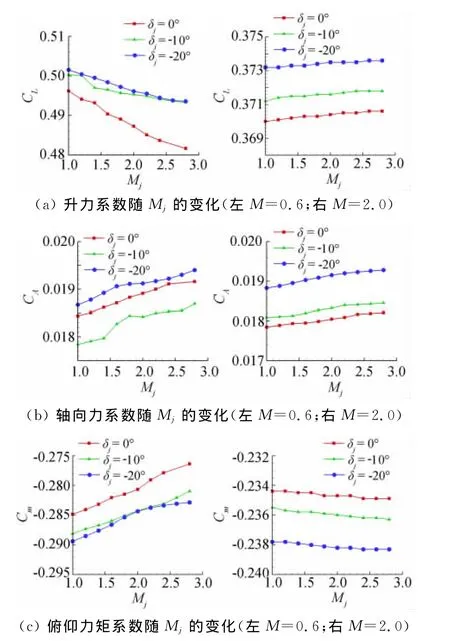
圖10 氣動力系數隨Mj變化Fig.10 Aerodynamic coefficient variation with Mj

2.5 噴流總溫

為考察噴流總溫的影響，以來流馬赫數為0.6和2.0，攻角為15°，噴口總壓為300kPa，噴流馬赫數為1.0為例，對噴口總溫分別取300K、900K、1200K、1800K時的計算結果進行比較和分析。

圖11（a～f）給出了不同噴口總溫時流場的溫度等值線分布。圖12分別給出了來流馬赫數為0.6和2.0時氣動力系數隨噴流總溫的變化。總的來看，可有如下結論：

（1）噴流總溫對尾噴流流場結構有一定影響，甚至改變流場結構的拓撲形態。噴流總溫增高時，噴管出口靜溫增高，由于噴流總壓固定，噴管出口靜壓不變，根據狀態方程，則噴管出口密度降低，噴流噴出后，進一步膨脹的能力減弱，即噴流的穿透力減弱。因此，M＝0.6時，噴流總溫增高，噴流馬赫盤減小，噴流總溫達900K時，馬赫盤即已消失，成為斜激波相交形態，噴流總溫進一步增大，則斜激波相交點前移；M＝2.0時，噴流總溫增大，斜激波相交點前移。

（2）噴流總溫雖對流場結構有一定改變，但局限于噴管以后的噴流尾跡區域，因此，噴流總溫變化對全機氣動力特性的影響甚小，幾乎可忽略不計。

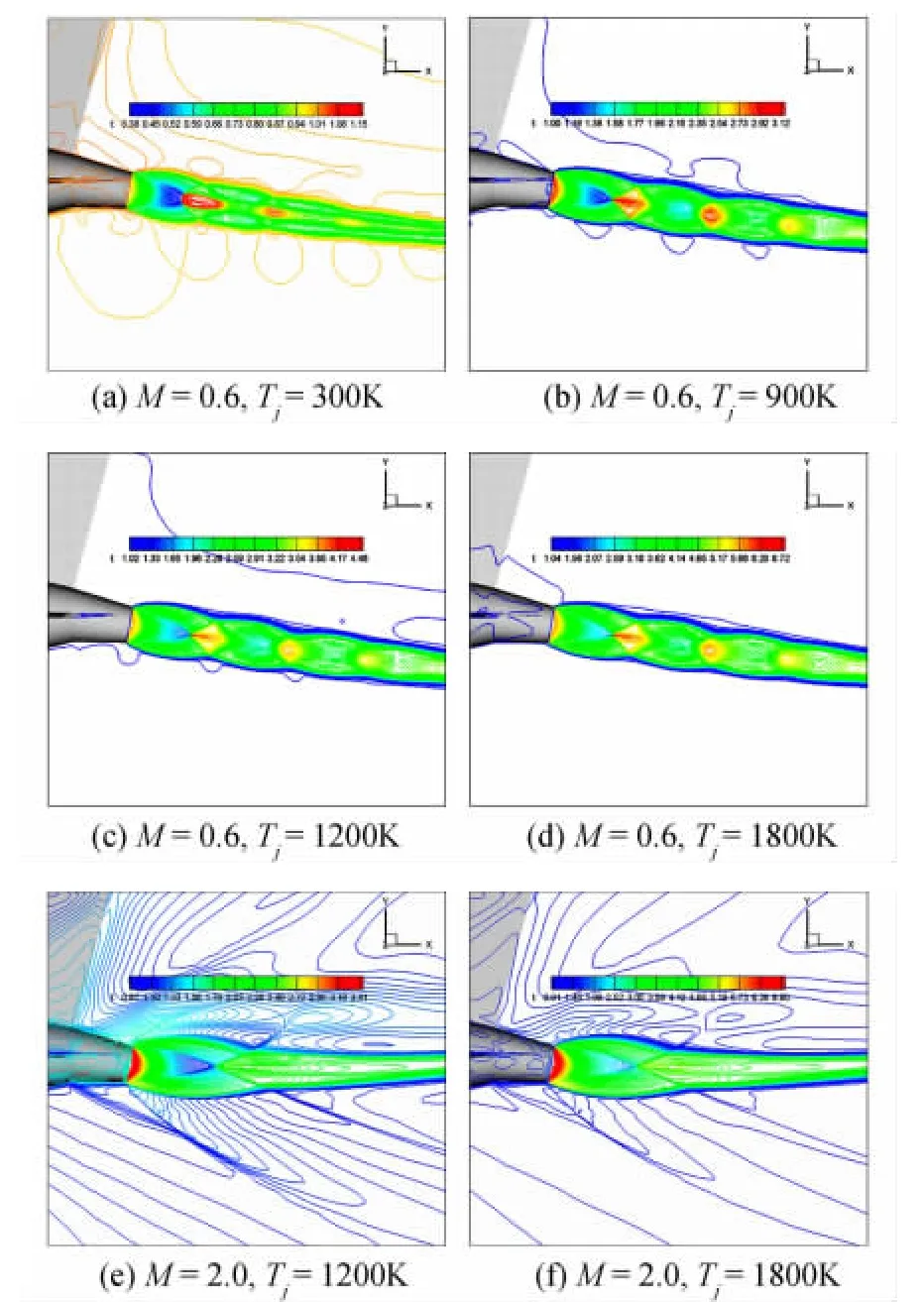
圖11 δj＝－10°時溫度等值線分布圖Fig.11 Temperature contours forδj＝－10°

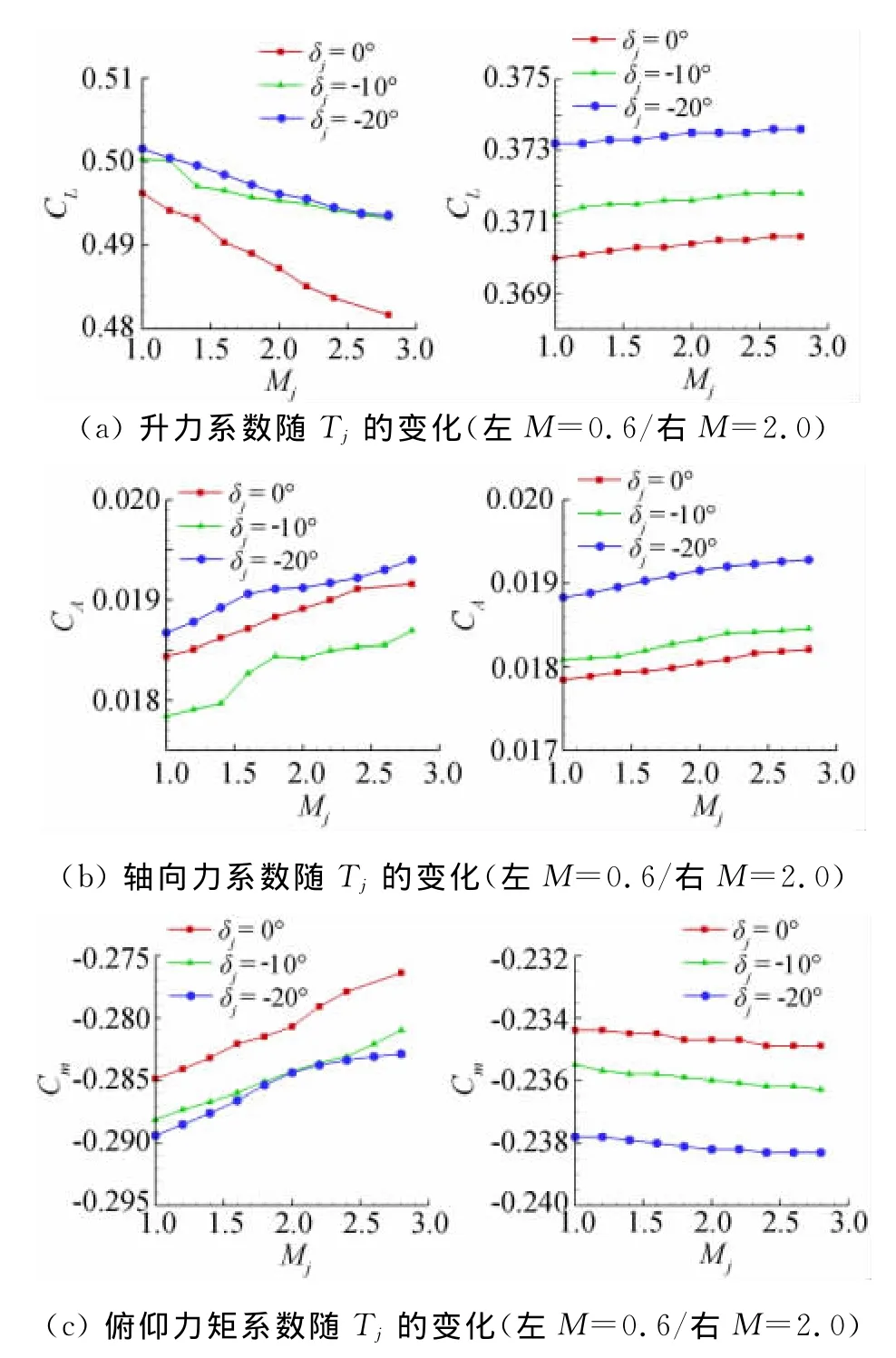
圖12 氣動力系數隨Tj變化Fig.12 Aerodynamic coefficient variation with Tj

3 結 論

本章針對一種簡化戰斗機風洞試驗模型，開展了推力轉向噴流與高速主流干擾的數值模擬研究，較為系統地研究了來流馬赫數、飛行攻角、噴流總壓、噴流馬赫數、噴流總溫、推力轉向噴管偏轉角等參數對流場結構和全機氣動特性的影響規律。根據研究結果和研究體會，可小結如下：

（1）主要的影響參數是來流馬赫數、飛行攻角、推力轉向噴管偏轉角和噴流落壓比，其它參數的影響較小。

（2）對流場結構影響最大的參數是來流馬赫數，其次是攻角和推力轉向噴管偏轉角。在來流馬赫數為0.6時，在大攻角下，推力轉向噴流的引射效應誘導出一定的超環量效應，但還需要進一步的驗證。

（3）對推力矢量角損失影響最大的參數也是來流馬赫數，其次是推力轉向噴管偏轉角和攻角。推力矢量角損失隨馬赫數、噴管偏轉角和攻角的增大而增大。在超聲速情況下，推力矢量角損失可超過噴管偏轉角的一半以上，使得推力矢量技術效率降低。因此，在超聲速條件下，推力矢量技術實際上并不可行。

（4）對全機氣動特性影響最大的參數是攻角，其次是來流馬赫數和推力轉向噴管偏轉角。但總的來說，由于簡化戰斗機的主翼為平板翼、尾噴管離主翼距離偏大，導致推力轉向噴流／高速主流干擾效應對全機氣動力系數的影響較小，對試驗測量提出了很高的挑戰。

以上結論對后續風洞試驗有一定的指導意義，本文計算研究也需要進一步與試驗研究相結合，相互校核，以提高計算結果的置信度。

［1］HILEY P E，WALLACE H W，BOOZ D E.Study of nonaxisymmetric nozzles installed in advanced fighter aircraft［J］.J.of Aircraft，1976，13（12）：1000－1006.

［2］司芳芳.推力轉向噴流與高速主流干擾的數值模擬研究［D］.［碩士學位論文］.中國空氣動力研究與發展中心，2010.

［3］FRED K，HARVEY S.X－31flight test update［R］.AIAA－92－1035.

［4］BOWERS A H，PAHLE J W.Thrust vectoring on the NASA F－18high alpha research vehicle［R］.NASA TM 4771，1996.

［5］CAPONE F，SMERECZNIAK P，SPETNAGEL D.Comparative investigation of multiplane thrust vectoring nozzles［R］.AIAA－92－3263.

［6］DEERE K A.Summary of fluidic thrust vectoring research conducted at NASA langley research center［R］.AIAA 2003－3800.

［7］連永久.射流推力矢量控制技術研究［J］.飛機設計，2008，28（2）：19－24.

［8］張群鋒，呂志詠.軸對稱矢量噴管外流對內流干擾研究［J］.航空動力學報，2003，18（3）：322－326.

［9］李棟，焦予秦，宋科.噴流－外流干擾流場數值模擬［J］.航空動力學報，2008，29（2）：292－296.

［10］王延奎，張永生.矢量噴流對細長體大迎角非對稱流動影響研究［J］.力學學報，2007，39（3）：289－296.