水面艦船附近氣泡運動數值模擬

王詩平 張阿漫 程瀟歐 姚熊亮 陳海龍

哈爾濱工程大學船舶工程學院，黑龍江哈爾濱 150001

0 引言

當在自由面與水中結構物附近產生氣泡時，需要同時計入兩者對氣泡脈動的影響［1-2］。水下爆炸被廣泛應用于國防和工業等領域，其生成氣泡的運動特性由于浮力和邊界的特性而非常復雜。當氣泡在剛性壁面附近運動時，剛性壁面會對氣泡產生吸引而誘導其產生朝向剛性壁面方向的射流；當氣泡在自由面附近運動時，自由面會對氣泡產生排斥而使射流方向遠離自由面，浮力的存在會使氣泡的運動形式更加復雜［3］。在數值模擬中描述在壁面、自由面和浮力共同作用下氣泡運動特性的研究較少，為此，本文將以計入自由面效應的格林函數替代基本格林函數，采用邊界元法研究水面艦船附近氣泡的運動特性，同時計入浮力的影響。

在對自由面進行建模時，需要將自由面區域設置得較大，或者將自由面建成封閉的四面體，這就導致自由面網格劃分較多［4］，嚴重影響計算速度。因此，本文將采用修正格林函數，在不對自由面進行建模的情況下考慮自由面對氣泡脈動的影響。

在考慮水下爆炸氣泡與水面艦船的相互作用時，由于藥包在水下爆炸生成的氣泡與自由面較近，因此需要考慮自由面對氣泡運動的影響，此時，在建立氣泡運動模型時，需要同時考慮氣泡表面、自由面和艦船水線面以下的部分。如此，就會產生一系列的問題：首先，自由面需要大量的三維網格，這樣會增加數值計算量；其次是自由面與結構的交界，這不僅會導致數值的不穩定，而且在處理結構與自由面的交界處時會帶來復雜的數值步驟。因此，本文將采用一種新的方法計算自由面與水面艦船附近氣泡的運動，通過在氣泡和水面艦船鏡像位置分布點匯，使得在計算過程中避免了對自由面建模的必要，從而提高計算速率。

1 數值模型及有效性驗證

假定水下爆炸氣泡周圍的流場為無粘、無旋且不可壓縮的理想流體，滿足拉普拉斯方程［5-7］：

下面，建立此鏡像法的數學模型。按照此方法，只需建立水面艦船的水下部分，艦船水面以上的部分則可忽略。圖1所示為水面艦船（水下部分）、爆炸氣泡及其鏡像，其中水面艦船的船長為L，船寬為B，吃水為H。在數值計算中，將水面艦船及其鏡像劃分為3個區域：水面艦船自由面以下部分（S＋）、水線面結點（I）以及水面艦船自由面以下部分的鏡像（S-）。氣泡表面及氣泡表面的鏡像分別表示為B＋和B-。在此種情況下，可將拉普拉斯方程表示成如下邊界積分方程：

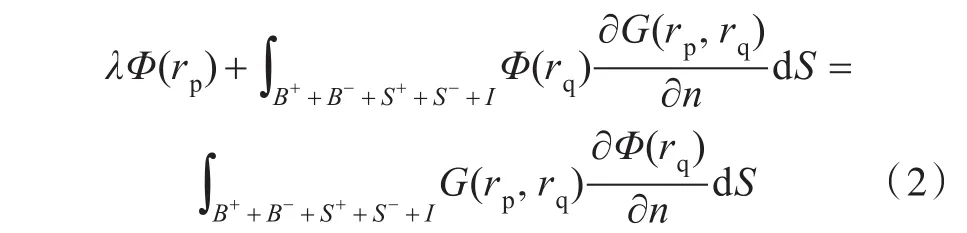
式中，rp為固定點；rq為積分點；λ為流場中的立體角。方程（2）聯系速度勢Φ和法向速度

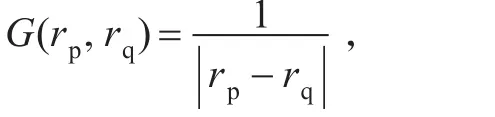
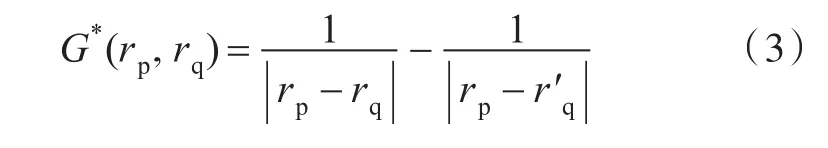
式中，r′q表示rq關于水平面z=0的鏡像點。則此時邊界積分方程可表示為：

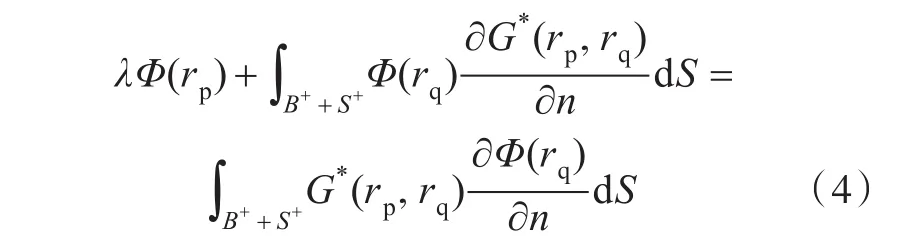
從方程（4）中可以看出，采用考慮自由面效應的格林函數取代基本格林函數后，邊界積分方程得到了簡化，僅需在船體水線以下部分和氣泡表面分布源和偶極即可得到計入自由面效應的邊界積分方程。

氣泡脈動過程滿足如下伯努利方程：

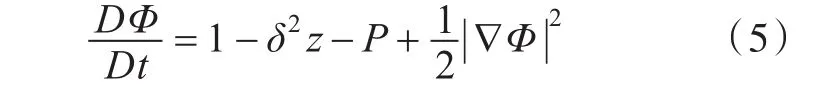
式中，δ為無量綱浮力參數，伯努利方程的無量綱化參考。本文將均采用無量綱變量，上述方程的無量綱化過程參考文獻［9］。

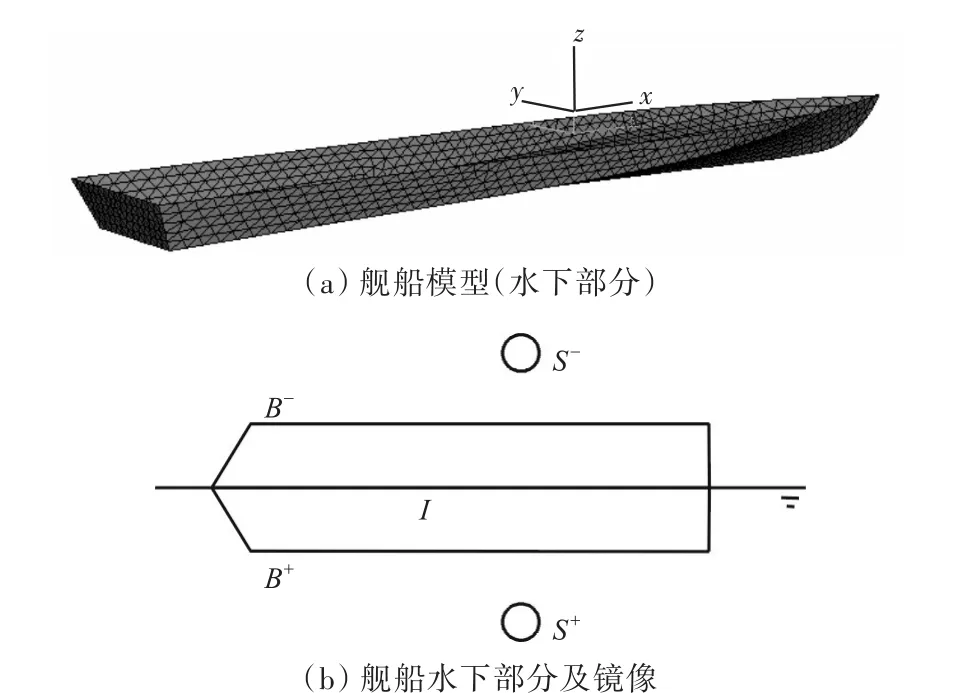
圖1 艦船模型和水下部分及其鏡像Fig.1 Ship model’s underwater part and its image

采用此格林函數可以計及自由面對氣泡動態特性的影響，下面將檢驗該方法在不建立自由面網格的基礎上考慮自由面效應的有效性。采用本文的格林函數運用三維模型進行計算，并將計算結果與自由面附近軸對稱氣泡運動特性的數值結果進行了比較。本文選取初始無量綱距離d＝1.4，強度參數 ε＝200，浮力參數 δ＝0，比熱比 γ＝1.25，對應氣泡初始半徑 R0＝0.116。將氣泡表面劃分成642個結點，1 280個單元。兩種結果的對比如圖2所示。圖2（a）～圖2（c）是采用考慮了自由面效應的三維氣泡脈動結果，在計算過程中沒有對自由面進行建模，圖中，z＝0的位置即為自由面的位置。圖 2（e）～圖 2（f）是在相同參數下采用軸對稱程序的計算結果。對于三維數值模擬，氣泡初始為球形，然后迅速膨脹，在t＝0.75時刻膨脹至最大體積（圖2（a）），隨后，氣泡開始坍塌，并在 t＝1.53時刻形成向下的射流（圖2（b）），在t＝1.64時刻，形成扁平的寬射流（圖2（c））。在整個計算過程中，氣泡的整體位置是向下移動的，其計算結果與圖2（d）～圖2（f）中列出的軸對稱結果相似。由圖中可看到，采用考慮了自由面效應的格林函數的結果與采用基本格林函數的二維軸對稱氣泡的結果基本相同，氣泡都在自由面的Bjerknes力作用下產生了遠離自由面的射流。在基于不同方法的氣泡脈動過程中，無量綱體積隨無量綱時間的變化曲線如圖3所示。由圖3可看出，采用考慮了自由面效應的格林函數計算的體積與軸對稱模型吻合較好，驗證了本文數值方法的有效性。

在處理水面艦船問題時，水面艦船被自由面分割成水上部分和水下部分，忽略水上部分后，邊界不再封閉，因此，在計算奇異積分時，Hii=4π-Hij的性質不再成立。邊界上立體角的求解可以通過如下2種方法求解。

圖2 自由面附近單個氣泡三維結果與軸對稱結果對比Fig.2 Comparison of three dimensional and axisymmetrical single bubble near free surface

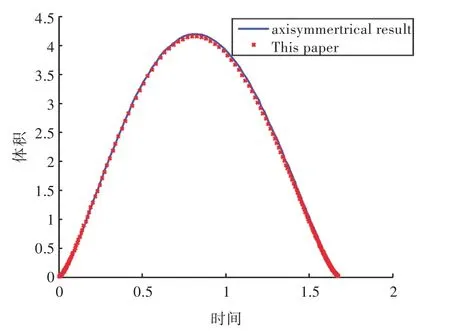
圖3 三維與軸對稱氣泡無量綱體積隨無量綱時間的變化曲線Fig.3 Time history of bubble dimensionless volume of 3D and axisymmetrical result

1）每個小的球三角形（例如，球三角形NBC）的面積可以通過下面的積分求得［10］：

其中φ0和θ的關系可以從圖4中找出。圖中，點O′為邊界上的結點，ON是點O′的單位法向量，弧AB，BC，CD，DE和EA分別是以 O′點為原點的單位圓與線性單元（延長線）的交界線。這樣，點O′的立體角λ便可以表示為弧ANB，BNC等球三角形的面積之和。

2）邊界立體角可通過如下方法求解［11］：

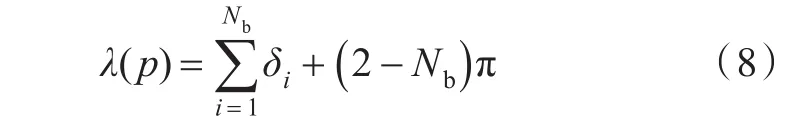
式中，Nb為結點 p周圍三角形的個數；δi為兩個相鄰三角形單元的角度。

2 數值結果

本文計算氣泡的代碼采用Fortran語言編寫，采用有限元軟件ABAQUS進行后處理，以實現計算過程可視化。考慮初始質量為N kg TNT的藥包安置在船體正下方0.4L的位置。氣泡脈動過程如圖5所示。圖5（a）為初始氣泡，在氣泡內部充滿了高溫高壓氣體，隨后氣泡迅速膨脹，在船體表面中部壓力最大。在t＝0.51時刻，氣泡體積達到最大然后便開始坍塌，在t＝1.04時刻，氣泡開始產生向上的射流，在t＝1.08時刻，環狀氣泡形成，并在t＝1.11時刻體積達到最小。不同時刻艦船表面的壓力分布如圖6所示。由圖中可看出，在t＝0的初始時刻和環狀氣泡體積最小的時刻（t＝1.11）附近，短時間內船體表面承受的垂向載荷數值很大，對艦船表面產生了類似“中拱”的巨大力矩，這時，結構處于危險狀態。在其余的絕大部分時間內，艦船表面的垂向載荷均很小。

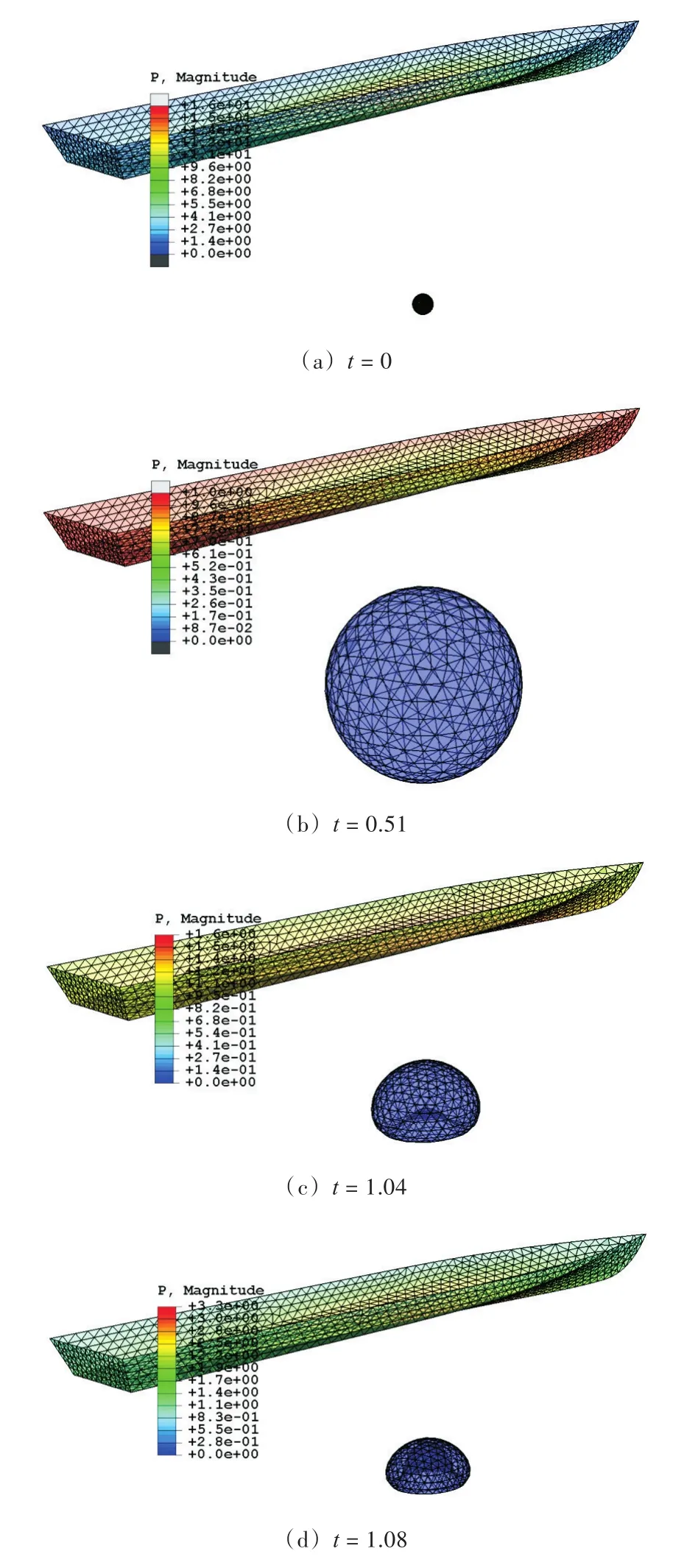
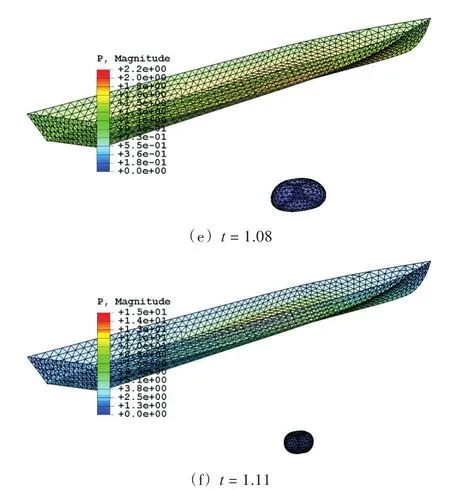
圖5 N kg TNT藥包距離水面0.4L爆炸生成氣泡的動態特性Fig.5 Bubble dynamics generated by N kg TNT at 0.4L depth

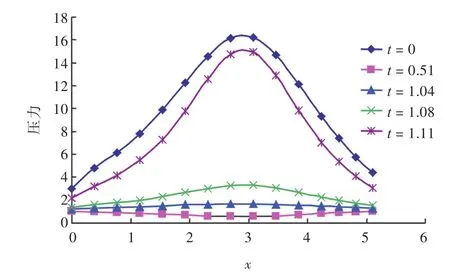
圖6 艦船表面沿船長方向的無量綱垂向載荷分布Fig.6 Dimensionless vertical load distributing on ship surface

艦船表面中點的氣泡載荷時歷曲線如圖7所示。艦船遭受氣泡作用的載荷與氣泡本身的運動息息相關，在氣泡脈動的絕大部分時間內，氣泡為近似球形，氣泡脈動速度較慢，艦船表面始終維持著低于靜水壓力的壓強值；在氣泡初始時刻和環狀氣泡體積最小時刻附近，艦船遭受著危險載荷，且射流在沖破氣泡壁的瞬間還會對艦船表面產生較大的射流沖擊載荷，計算值為14.83。射流沖擊主要是對結構造成局部性損傷，并有可能在流場中產生空化，射流沖擊的特性還有待進一步的探索。

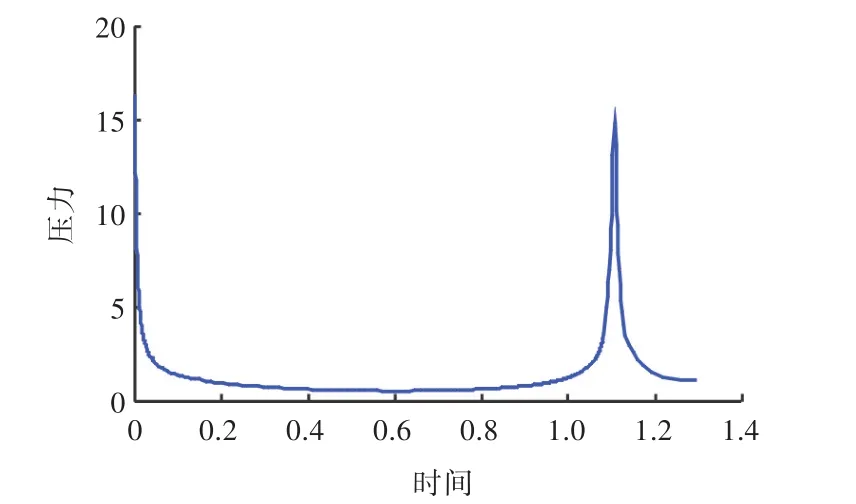
圖7 艦船表面中點無量綱垂向載荷時歷曲線Fig.7 Dimensionless vertical load of bubble on middle ship surface

當水下爆炸不是發生在艦船正下方，例如，發生在舷側與水面附近時（圖8），舷側的存在使得氣泡產生朝向舷側曲面的射流，而自由面的存在又使得氣泡產生朝向遠離自由面的射流，在這兩股影響下，氣泡便產生斜向下的射流，具體實驗過程參見文獻［12］。因此，當藥包在自由面和舷側附近爆炸時，氣泡的攻擊效果會被削弱。下面，將模擬水下爆炸氣泡在舷側和自由面附近的情況，在計算過程中，采用鏡像方法考慮了自由面對氣泡脈動的影響。

圖8 自由面附近氣泡對舷側的攻擊效果Fig.8 Attack effect of bubble near shipboard and free surface

初始質量為N kg TNT的藥包安置在船體正下方0.3L，左側0.55B的位置處。氣泡脈動過程如圖9所示，其中，圖中云圖表示壓力。此工況為靠近水面艦船和自由面的情況，艦船和自由面對氣泡脈動的影響都很大。在此算例中，藥包距離船體較近，在氣泡膨脹至最大體積的過程中，艦船對氣泡有阻礙作用，而在氣泡坍塌的過程中，船體對其的吸引較劇烈，氣泡在靠近船體一側較大，形成了遠離自由面和靠近艦船的斜射流。

初始質量為N kg TNT的藥包安置在船體正下方0.3L、左側0.8B的位置處。氣泡脈動過程如圖10所示，其中，圖中云圖表示壓力。在此算例中，藥包距離船體較遠，受船體的吸引較小，氣泡在膨脹至最大體積附近時受到了艦船輕微的排斥，而在坍塌過程中則受到了艦船的吸引。與上一算例相比，氣泡被船體吸引較小，氣泡射流向下。

如果水下爆炸氣泡出現在水中結構物附近，通常會形成一股朝向水中結構物的射流，這股射流非常大（速度將達到100 m/s，甚至更大），并有可能會對水中結構物造成毀傷。根據氣泡與水中結構物的相對位置，由于近自由面和浮力的影響，氣泡射流可能會作用在水中結構物上，也有可能不會直接作用在結構上。

3 結 語

對于水面艦船，自由面的存在不僅增加了網格的數量，而且在自由面與結構的交界處也增加了數值處理的難度。本文采用考慮了自由面效應的格林函數來取代基本格林函數，計入自由面的存在對氣泡運動的影響，并將計算結果與軸對稱數值模擬結果進行了對比，數值結果吻合良好。

通過數值模擬和實驗發現，當藥包在舷側和自由面附近爆炸時，氣泡射流可能不會完全作用在艦船上，自由面效應的存在削弱了氣泡的打擊能力。因此，在指導常規武器攻擊水面艦船時，為充分發揮氣泡射流的威力，應盡量避免其在自由面附近爆炸。

［1］KLASEBOER E，KHOO B C，HUNG K C.Dynamics of an oscillating bubble near a floating structure［J］.Journal of Fluid and Structures，2005，21（4）：395-412.

［2］COLE R H.Underwater explosion［M］.New Jersey：Princeton University Press，1948：118-127.

［3］張阿漫，王詩平，汪玉，等.水下爆炸對艦船結構損傷特性研究綜述［J］.中國艦船研究，2011，6（3）：1-7.ZHANG A M，WANG S P，WANG Y，et al.Advances in the research of characteristics of warship structural damage due to underwater explosion［J］.Chinese Journal of Ship Research，2011，6（3）：1-7.

［4］張阿漫，姚熊亮.近自由面水下爆炸氣泡的運動規律研究［J］.物理學報，2008，57（1）：339-353.ZHANG A M，YAO X L.The law of the underwater explosion bubble motion near free surface［J］.Acta Physica Sinica，2008，57（1）：339-353.

［5］WANG Q X，YEO K S，KHOO B C，et al.Unstructured MEL modelling of unsteady nonlinear ship waves［J］.Journal of Computational Physics，2005，210 （1）183-224.

［6］ZHANG Y L，YEO K S，KHOO B C，et al.3D jet impact and toroidal bubbles［J］.Journal of Computational Physics，2001，166（2）：336-360.

［7］宗智，何亮，孫龍泉.水下爆炸氣泡對水面艦船載荷的數值研究［J］.船舶力學，2008，12（5）：733-739.ZONG Z，HE L，SUN L Q.Numerical study of loading on the surface ship near an underwater explosion bubble［J］.Journal of Ship Mechanics，2008，12（5）：733-739.

［8］WANG C，KHOO B C.An indirect boundary element method for three-dimensional explosion bubbles［J］.Journal of Computational Physics，2004，194（2）：451-480.

［9］戴遺山，段文洋.船舶在波浪中運動的勢流理論［M］.北京：國防工業出版社，2008.

［10］ZHANG Y L，YEO K S，KHOO B C，et al.Three-dimensional computation of bubbles near a free surface［J］.Journal of Computational Physics，1998，146（1）：105-123.

［11］WANG Q X.Numerical modelling of violent bubble motion［J］.Physics of Fluids，2004，16（5）：1610-1619.

［12］張阿漫，王詩平，白兆宏，等.不同環境下氣泡脈動特性實驗研究［J］.力學學報，2011，43（1）：71-83.ZHANG A M，WANG S P，BAI Z H，et al.Experimental study on bubble pulse features under different circumstances［J］.Acta Mechanica Sinica，2011，43（1）：71-83.