一道典型力學習題的新解
蔣 濤 (長江大學工程技術學院,湖北 荊州 434020;長江大學地球物理與石油資源學院,湖北 荊州 434023)
朱 科 (長江大學工程技術學院,湖北 荊州 434020)
一道典型力學習題的新解
蔣 濤 (長江大學工程技術學院,湖北 荊州 434020;長江大學地球物理與石油資源學院,湖北 荊州 434023)
朱 科 (長江大學工程技術學院,湖北 荊州 434020)
在求解力學問題的過程中,建立適當的參考系與坐標系將給解題帶來極大方便。從一道典型力學習題出發 ,介紹了2種新解法,分別在非慣性系中建立直角坐標系、在慣性系中利用直角坐標系下的運動約束方程進行了求解。并對新解法的求解思路和方法作了簡單點評。
慣性系;非慣性系;慣性力;運動約束方程
如圖1所示,一輕繩2端分別連接小球A和小環B,球與環質量相等,環B可在拉緊的水平鋼絲上作無摩擦的滑動。現使小球在鋼絲所在的豎直平面內擺動,求小球擺離鉛垂線最大角度時小環B和小球A的加速度aB和aA[1]。
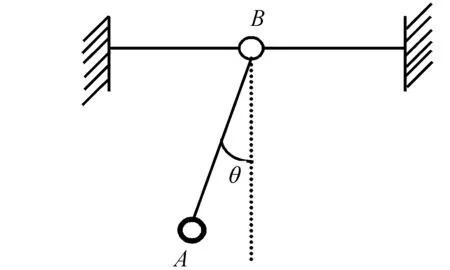
圖1 球A和環B 組成的系統
文獻[2]中介紹了3種典型的解法:第1種采用非慣性系求解,利用了小球A的法向(沿A、B連線方向)加速度為零這樣一個輔助條件;后2種解法采用地面參考系求解,利用了在地面參考系中A和B的加速度在它們連線的方向上的分量相等這個輔助條件。通觀這些解法,一方面深感這些輔助條件不太容易被人想到,另一方面覺得這些解法都稍顯麻煩。筆者經過深入思考,提出2種簡便新穎的解法。
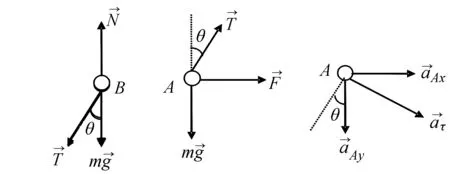
圖2 球A的受力分析、加速度分解及環B的受力分析圖
于是有:
由以上方程可解得:
所以A相對于地面的加速度為:
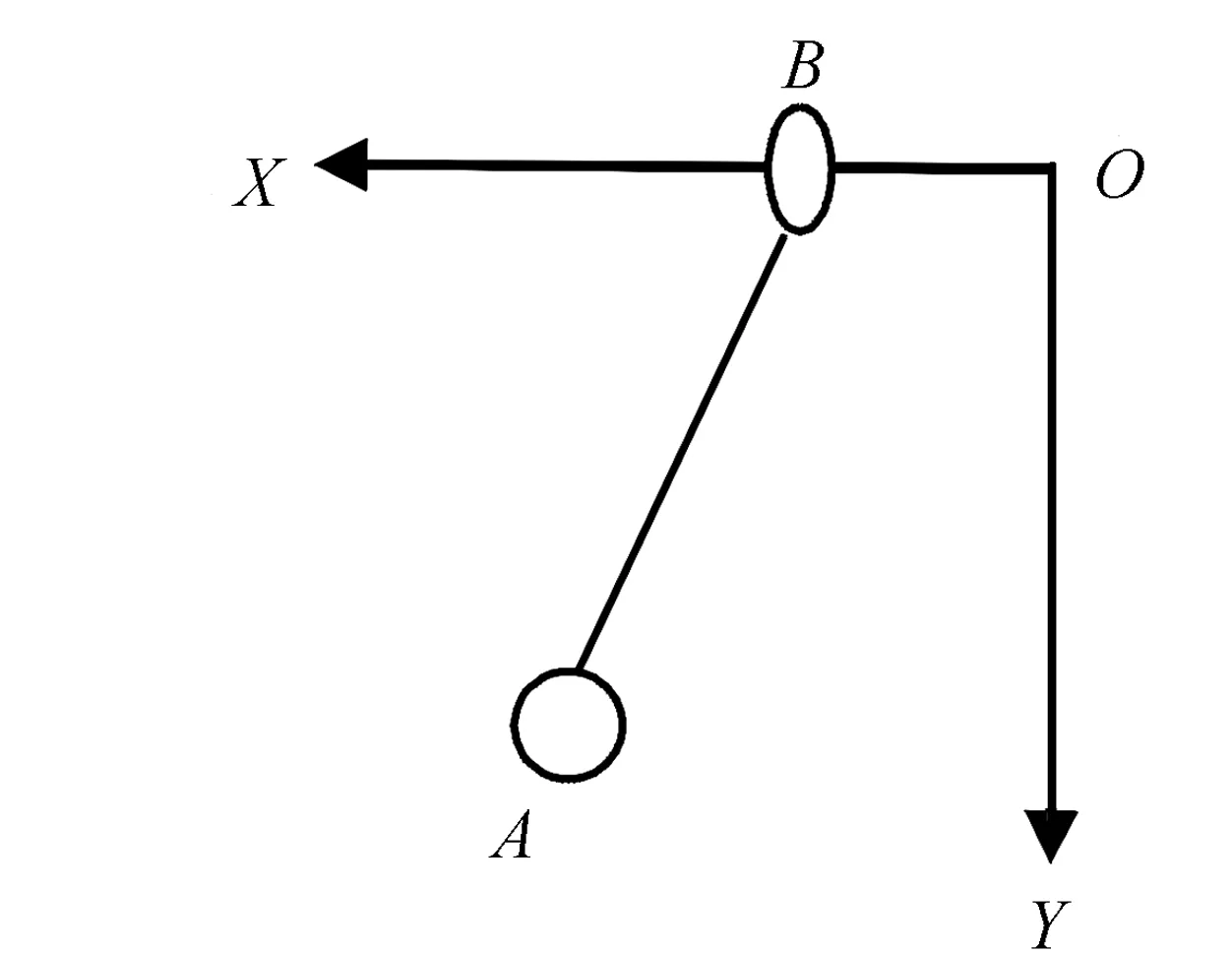
圖3 A、B在 XOY坐標中的位置
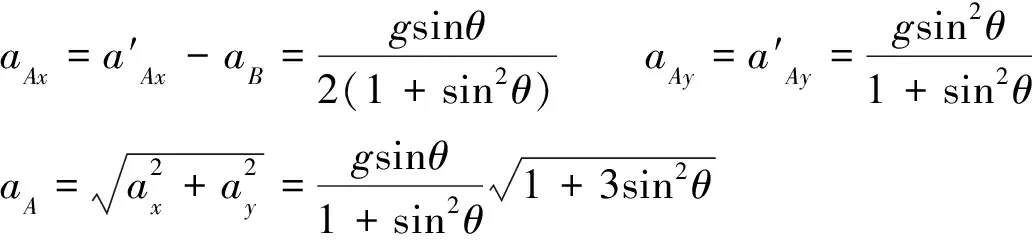
從上述可見,筆者的方法是在非慣性系中建立直角坐標系求解,這里關鍵的一點是得到加速度與偏角的關系式。較之文獻[2]中標準解法是在非慣性系中建立自然坐標系求解,顯然筆者的方法更簡單。這表明不同坐標系的選擇對求解的繁簡程度有很大的影響,選擇適當的坐標系能使求解過程更簡單。
解法2選擇輕繩為參考系,在慣性參考系中求解。建立如圖3直角坐標系,其中輕繩長度為l,A、B任意時刻在鉛錘面XOY坐標系中的坐標分別為(xA,yA)、(xB,yB)。
可得到如下的運動約束方程:
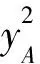
方程兩邊對時間求導,整理后得:
(1)
當小球擺離鉛垂線最大角度時有:
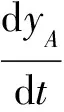
(2)
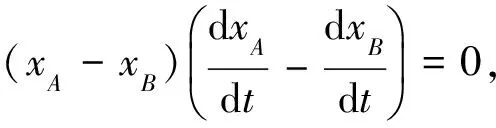
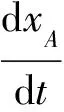
(3)
即:
υAx=υBx
(4)
再將方程(1)兩邊對時間求導,整理得:
(5)
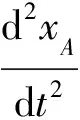
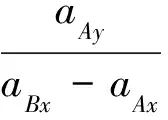
(6)
對環A、球B受力分析如圖4所示,其中T為繩子中的張力,N為水平鋼絲對B的支撐力。列出如下動力學方程:
Tsinθ=maBxTsinθ=-maAxmg-Tcosθ=maAy
可以解出:
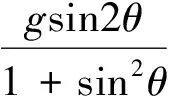
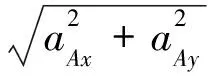
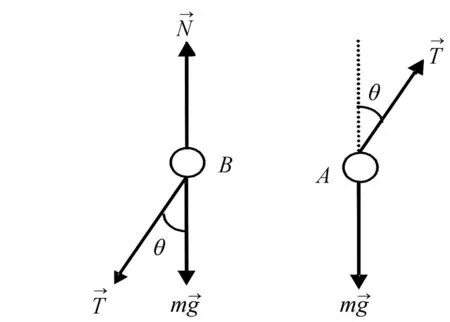
圖4 球A、環B的受力分析圖
從上述可見,筆者的方法是在慣性系中建立直角坐標系求解,這里關鍵利用了運動約束方程得到一個加速度與偏角的關系式(6),比文獻[2]解法2、3的輔助條件來得簡單直接,后者必須加以詳細闡述(事實上利用從運動約束方程導出的式(4)及向心力公式能夠滿意地得出文獻[2]中解法2、3的輔助條件)。雖然看上去解答過程似乎有點長,但是思路簡單。
綜合上述,筆者給出了文獻[2]之外的2種新穎簡便的解法,由此可以看出深入發掘題目內涵、建立適當的參考系與坐標系將給解題帶來極大方便。
[1]吳錫瓏.大學物理教程(第2冊)[M].第2版.北京:高等教育出版社,1999.
[2]李銅忠,董占海,袁曉忠,等.一道典型力學習題的多種解法[J].物理與工程,2007,17(3):59-60.
[編輯] 洪云飛
10.3969/j.issn.1673-1409(N).2012.02.045
O3-4
A
1673-1409(2012)02-N134-02
2011-10-25
蔣濤(1978-),男,2002年大學畢業,講師,博士生,現主要從事大學物理方面的教學與研究工作。

