熱層大氣密度變化特征與太陽輻射和地磁指數的相關性分析

苗 娟，劉四清，李志濤，黃文耿，唐歌實

（1中國科學院空間科學與應用研究中心，北京100190；2航天飛行動力學技術重點實驗室，北京100094）

1 引言

大氣密度與低軌道航天器所受的大氣阻力緊密相關，是影響衛星軌道的重要因素。要準確預測航天器的軌道，就要對大氣密度做出精確的預報。從20世紀50年代開始，發展了多種半經驗的高層大氣模型，形成了 CIRA 系列[1]、Jacchia 系列[2]、DTM 系列[3，4]、MSIS 系列[5，6，7]等各種參考大氣模型，為空間活動提供服務。但由于高層大氣的變化極其復雜，幾十年來雖然大氣模型在不斷地改進和發展，但一般情況下模型仍存在15%～30%左右的誤差，在空間環境擾動期間可達100%甚至更高[8，9]。在航天器測定軌中，大氣密度模型誤差將轉化為軌道誤差，影響操控計劃、精密定軌、碰撞規避及航天器再入等。因此，如何提高大氣模型的預報精度是衛星和航天服務一直致力解決的重要問題。

2000年Tobiska[10]提出在模型中直接用E10.7來替代傳統的F10.7能提高SEM衛星軌道衰減的預報精度、2006年Bowman[11]等人建立了兩種新的太陽輻射指數S10.7和M10.7，建立了改進的大氣密度模型JB2006。2008年Bowman再次增加了一個新的太陽輻射指數Y10.7，并且引入了地磁指數Dst，建立了新模型JB2008[12]。

本文利用CHAMP衛星加速度儀資料反演的大氣密度數據，分析大氣密度變化與五種輻射指數和兩種地磁指數的變化關系，及發生磁暴時大氣密度的變化特征，并利用Dst指數對密度變化整體態勢進行預報和評估，為大氣密度模型的改進奠定基礎。

2 大氣密度與太陽輻射和地磁指數變化分析

CHAMP衛星是德國地球科學研究中心組織研制的一顆科學小衛星，于2000年7月15日發射，初始高度為454km、運行于傾角為87.3°近圓極軌道上，繞地周期約為90min。本文所采用的數據為美國科羅拉多大學CHAMP研究小組發布的2001年－2008年400km標準高度上的大氣密度，此段時間包括了第23太陽活動周峰年及整個下降階段，為開展大氣密度與太陽輻射、地磁暴的變化特征分析提供了充足的數據。

由于緯度、地方時的不同都能引起大氣密度的變化，為了突出地磁活動對密度的影響，消除地方時和緯度對密度的影響，文中對衛星運行一個軌道周期內的大氣密度進行了平均，以便更加清楚地分析大氣密度整體變化特征，并采用一個地方時周期為一個密度平均周期。

分別選擇2005年8月27日（F10.7為94，地磁ap指數均小于10）和2001年11月5－7日（F10.7最大為230，ap最大為300）作為平靜期和磁暴期的代表，圖1、圖2分別給出地磁平靜和磁暴兩種狀態下經過平均之后的大氣密度變化情況。由圖1可以看到，在同一天內，衛星運行各個軌道上的平均密度值變化不大，比較穩定，密度值維持在 1.3×10－12kg/m3，可以推算出密度對衛星軌道衰減的平均影響也比較穩定。圖2顯示，平均密度能夠清晰地反映出密度對磁暴響應的整個過程，并能給出密度的最大變化值和時間，可為軌道衰減幅度分析提供參考。因此可以說，一個軌道周期的平均密度，可以清晰反映密度的整體變化特征和趨勢，同時對軌道的平均變化也具有一定意義。

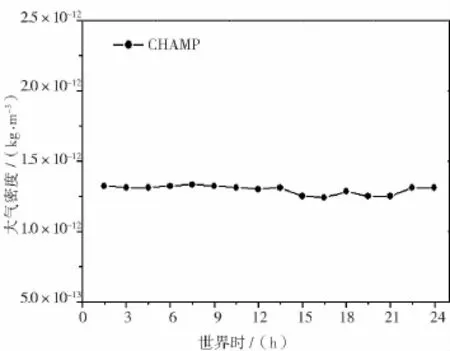
圖1 地磁平靜時平均密度變化

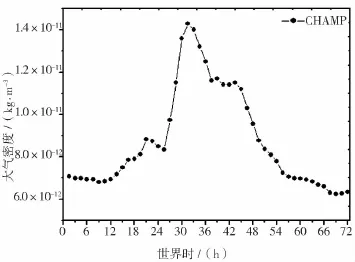
圖2 磁暴時平均密度變化

2.1 大氣密度隨太陽輻射指數的變化

以F10.7作為太陽輻射能量參數的大氣模型已經過了幾十年的發展，模型的誤差始終未能得到很好的改善，研究者開始尋求能夠表征太陽輻射能量的新參量，這比改變百萬行的原始大氣模型代碼容易得多[13]。對此，曾有研究者提出 E10.7，S10.7，M10.7，和 Y10.7等新的太陽輻射指數來改善大氣模型[10，11，12]。

新的輻射指數是否比傳統的F10.7能更好地表征太陽輻射對大氣密度的影響，本節對五種輻射指數和密度的變化關系進行統計分析。圖3給出了F10.7，E10.7，M10.7，S10.7，Y10.7五種太陽輻射指數的月均值比較，為了圖形能更清楚地展示各曲線的關系，本圖只給出了部分數據（2001－2004年）。明顯看出，五種指數的變化規律基本一致，E10.7整體略高于其它幾個指數，特別是在太陽活動高年期間更加明顯。圖4～圖8分別給出了大氣密度與五種輻射指數分布關系，可以看到密度的變化與五種指數變化趨勢一致，相關系統Ro0.97以上。同時也可以看到，在150sfu以下的相關性符合更好，這可能是由于在太陽活動低年，太陽上的突然爆發事件較少，大氣密度和太陽輻射相對都比較穩定。

從幾種太陽輻射指數與密度都具有很好相關性也可以得到，若不考慮每一種輻射指數的物理含義，單從數據統計意義上來表征輻射對密度的影響的時，任何一種輻射指數均能很好地反映密度的變化，這也可能是為什么長期以來大量模式采用易于獲取的F10.7來表征太陽輻射大小的原因之一。

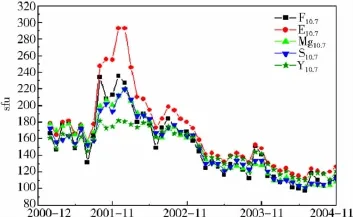
圖3 五種輻射指數的比較

圖4 大氣密度與F10.7

圖5 大氣密度與E10.7

圖6 大氣密度與M10.7

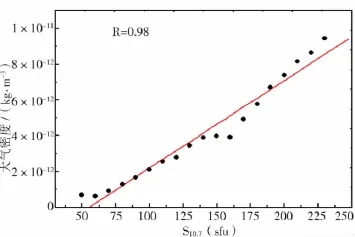
圖7 大氣密度與S10.7

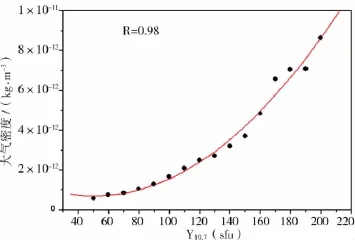
圖8 大氣密度和Y10.7

2.2 大氣密度隨地磁指數的變化

除太陽輻射指數外，一直以來地磁指數被作為大氣模式的輸入來表征地磁活動狀態對高層大氣的影響。在JB2008模式之前，各類參考大氣模式中主要采用Ap/ap/Kp指數作為模式輸入參數。2008年，Bowman在新建的JB2008模式中用Dst代替了ap指數[12]。

大氣密度與這兩種地磁指數的變化關系如何？本文對2001年－2008年400km高度的CHAMP衛星大氣密度與ap、Dst兩者的變化關系分別進行統計，圖9為密度和ap的變化關系，圖10為密度和Dst的變化關系。從圖可以看到，ap和Dst與密度的變化關系都分為兩個階段。對于ap指數，當ap≥50nT時，ap與密度呈線性相關，相關系數為0.84，而當ap<50nT時，兩者的關系更符合指數函數，其相關性為0.99；而對于Dst指數，當Dst≤0時，密度與其有很好的負相關性，線性相關系數達-0.95，而對于Dst＞0，兩者關系很難用一個線性或者指數函數表示。通過對Dst大于0的數據進行分析，除了在地磁平靜期Dst＞0之外，Dst的突然增加往往都是出現在磁暴前的急始階段。

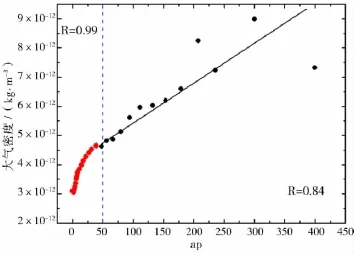
圖9 大氣密度與ap指數變化

圖10 大氣密度和Dst指數變化

從與密度的線性關系來看，Dst與密度變化更一致。這可能是由于ap指數是由Kp指數等效得到的，屬于分級指數，其值并不連續，在最小值0與最大值400之間分為28個等級，導致最多只能有28個格點對其進行統計，而Dst指數屬于無級指數，沒有人為設定的上下限和間斷，這也可能是導致ap指數與密度的線性相關性不如Dst的原因。

2.3 磁暴期間大氣密度變化特征

為了進一步分析磁暴對高層大氣的影響，本文對2001年－2008年Dst≤-50的60個磁暴事件中的密度及地磁指數ap、Dst進行了統計分析。主要分析磁暴的發生時間、大小和密度變化之間的關系。

事實上，一次典型磁暴的過程往往會伴隨太陽輻射的變化，而大氣密度的變化中必然包含了這部分影響。要分析不同地磁暴對密度的程度影響，就應剔除密度中太陽輻射變化帶來的影響，在同一輻射標準下比較才有意義。這就需要對60個磁暴的進行統一輻射水平“標準化”，即在其它條件不變的情況下把密度都標準化到同一個F10.7情況下，具體做法如下：

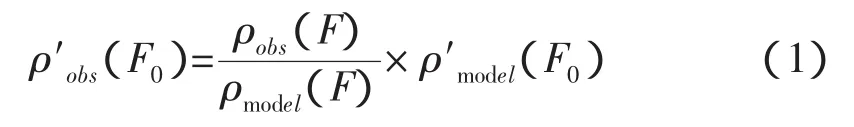
其中，ρobs（F）為實測密度，ρmodel（F）為實測太陽輻射指數下的模式計算密度，本文中采用的是NRLMISISE-00國際參考大氣模式，ρ′model（F0）為太陽輻射指數標準值情況下的模式計算密度，ρ′obs（F0）為標準后的大氣密度。

本文中把60個磁暴都標準化到同一太陽輻射水平150sfu后，分析密度、Dst、ap指數之間的變化關系。圖11（a）—（d）給出了4個較大磁暴事件的例子，圖中的藍色豎直虛線分別表示密度開始增長和恢復到磁暴前水平。通過比較密度、Dst和ap之間變化，可以看到：1）密度的變化和兩種地磁指數的變化時間都比較一致，但相比于ap，密度的開始上升時間與Dst的開始時間更加吻合；2）密度的恢復時間要比ap的恢復時間慢；但要比Dst恢復的快，對60個磁暴事件統計表明，大部分磁暴在Dst恢復至60%～80%時，密度就已恢復到磁暴前水平。3）圖11（b）給出的是 ap 指數同為 300，Dst分別為－373、－289的連續兩個磁暴過程，可以看到，兩個磁暴中的密度變化有較大差別，從變化幅度來看，密度的變化與Dst更加一致。

為了更進一步分析磁暴時密度的變化，對輻射指數標準化之后的60個磁暴事件進行統計，具體規定與做法如下：1）磁暴之前的水平：密度出現連續上升之前的幾點平均值密度值作為磁暴前的密度水平，對應的幾個點的平均Dst/ap為磁暴前的地磁水平，分別表示為 ρbegin，Dstbegin，apbegin；2）對一個磁暴事件，密度的最大值作為這個磁暴時的最大密度，Dst/ap的極值表征此次磁暴強度，分別表示為ρmax，Dstmax，apmax；3）當密度再次回到磁暴前的水平，表示磁暴對大氣密度的影響結束。對60個磁暴事例分別進行了 ρbegin，Dstbegin，apbegin，ρmax，Dstmax，apmax統計，圖12、13給出分別用Dst和ap表征最大磁暴與密度最大值之間的關系。

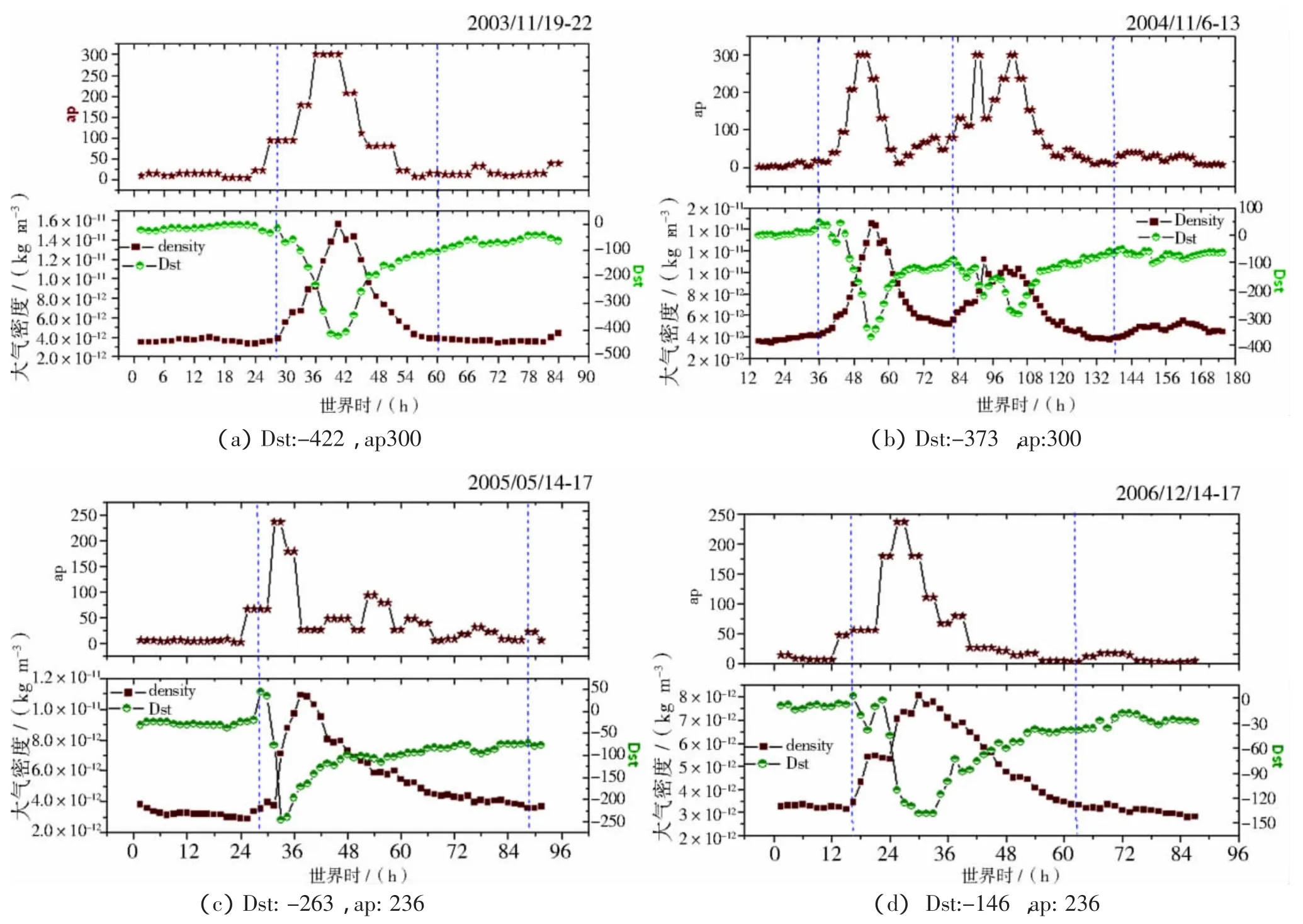
圖11 （a）－（d）大氣密度與 Dst、ap 的變化比較

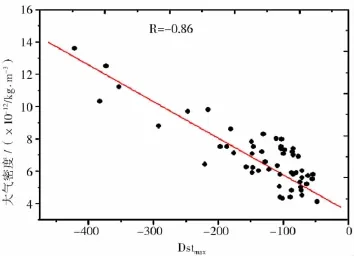
圖12 Dst與密度變化關系

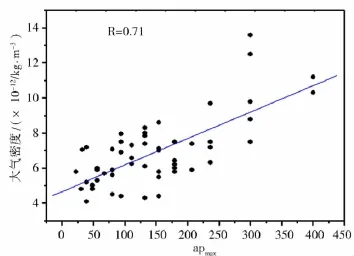
圖13 ap與密度變化關系

比較可以看到，無論用Dst還是用ap來表征磁暴程度，從總體趨勢來看，磁暴的大小與密度的變化是一致的，磁暴越大，密度增加幅度越大，這與前面總的統計結果一致；同時從個例來看，并非一個大磁暴對應的大氣密度一定大于一個小磁暴的密度，這個結論與陳光明的研究結果一致。分析其原因可能是由于磁暴對大氣密度的影響是一個復雜的過程，用一個地磁指數可能無法全面地描述它的變化；如果只用地磁指數表征磁暴期大氣密度的變化，兩個指數相比，Dst與密度之間的線性相關系數為-0.86，ap與密度之間的線性相關系為0.71，Dst與密度的相關性好于ap。

2.4 大氣密度和Dst的一元線性擬合

上面分析可以看到，無論是一般情況下，還是在磁暴事件中，密度的整體變化與ap、Dst指數都有很好的相關性，并且密度與Dst變化更一致。基于Dst和密度變化關系，可以建立一個密度、Dst之間的一元線性回歸方程，驗證是否可以通過Dst指數的變化就可以較好地預測、特別是磁暴時大氣密度的整體態勢變化，一元回歸方程如下：

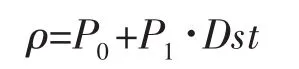
其中，ρ密度，Dst為地磁指數，P0，P1為待定系數。

預留出2003年的數據作為驗證之外，利用2001－2008年的其它所有CHAMP大氣密度數據和Dst進行P0、P1系數擬合，再用所擬合得到的系數及實際的Dst指數對2003年的密度進行計算，并與CHAMP實測結果及NRLMSISE-00模式計算結果進行比對。圖14是為2003年11月18－23日的一次磁暴過程，比較看出，模式對磁暴的反映很不足，而直接采用Dst值擬合的密度能很好地反映密度的整體態勢變化。為了進一步驗證擬合結果的適應性，用CHAMP擬合的系數對GRACE-A進行驗證，圖15為GRACE-A衛星2003年8月16－22日的一次磁暴過程，同樣可以看到，擬合結果比模式計算更接近于實測結果。

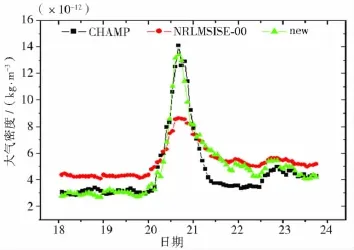
圖14 CHAMP驗證

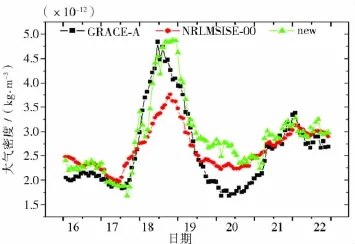
圖15 GRACE-A驗證

3 結論與討論

本文利用CHAMP衛星加速度儀資料反演的大氣密度數據，分析了 F10.7，E10.7，Mg10，S10，Y10 五種太陽輻射指數和兩種地磁指數Dst、ap與密度之間的變化關系，得到如下結論：

1）密度的變化與五種指數變化一致，相關程度都在0.97以上。若不考慮輻射指數的物理含義，如從數據統計意義上來表征輻射對密度的影響，任何一種輻射指數均能很好地反映密度的變化。

2）密度與地磁指數ap、Dst的變化都具有很好的相關性，通過對60個磁暴事例的統計，可看到在磁暴期，無論從上升時間及增加幅度上，密度的變化與Dst更加一致，這可以為今后模式的建立和改進提供參考。

3）在密度與Dst變化關系的基礎上，建立一種簡單的利用Dst指數預測大氣密度整體態勢變化的擬合關系，通過對CHAMP和GRACE-A兩個衛星的驗證，可以看到大氣密度整體態勢的變化能夠通過Dst指數的變化很好地反映出來，并且比利用國際參考大氣NRLMSISE-00計算的結果更接近觀測值，這可以為航天器測定軌提供參考。

本文研究的數據是以CHAMP為基礎，通過GRACE-A數據進行了適應性驗證，但因這兩顆衛星同屬于極軌衛星，對于其它軌道傾角衛星的適用性還有待于進一步的分析。同時，本文中只構建了密度和Dst的一元線性回歸關系，暫時未考慮ap指數，而鑒于ap指數的通用性和對Dst的互補性特征，后期將進一步開展大氣密度與兩種指數的加權分析。

［1］H.Kallmann-Bijl，R.L.F.Boyd，H.Lagow，S.M.Poloskov，and W.Priester （eds.）.Cira 1961:Cospar International Reference Atmosphere 1961，North-Holland Publishing Company，Amsterdam，1961.

［2］Jacchia，L.G..New static Models of the thermosphere and exosphere with empirical temperature models.Technical Report 313，Smithsonian Astrophysical Observatory，1970.

［3］Berger，C.，Biancale，R.，Ill，M.，Barlier，F.Imporvement of th empirical thermosphere model DTM:DTM-94—a comparative review of various temporal variations and prospects in space geodesy applications.Journal of Geodesy 72（3），161-178，1998.

［4］Bruinsma，S.，Thuillier，G.，Barlier，F..The DTM-2000 empirical thermosphere model with new data assiminlation and constraints at lower boundary:accuracy and properties，Journal of Atmosphere and Solar-terriestrial Physics65，1053-1070，2003.

［5］Hedin，A..MSIS-86 thermosphereic model.Journal of Geophysical Research 92（A5），4649-4662，1987.

［6］Hedin，A.E.Extention of the MSIS thermospheric model into the middle and lower atmosphere.Journal of Geophysical Research 96（A2），1159-1172，1991.

［7］Picone，J.，Hedin，A.，Drob，D.，Aikin，A..NRLMSISE-00 empirical model of the atmophere:statistical comparisons and scientific issues.Journal of Geophysical Research 107（A12），2002.

［8］Marcos，F.，Bass，J.，Baker，C.，Boner，W..Neutral density models for aerospace applications.In:32nd Aerospace Sciences Meeting and Exhibit，January 10－13，1994/Reno，NY，1994

［9］Rhoden，E.，Forbes，J.，Marcos，F..The influence of geomagnetic and solar variabilities on lower thermosphere density.J.Atmos.Sol.-Terr.Phys.62，999－1013，2000

［10］Tobiska W K..Validating the solar EUV proxy E10.7.J Geophys Res，2001，106（A12）:29969—29978

［11］Bowman，B.R..The JB2006 empirical thermospheric density model，Journal of Atmospheric and Solar-Terrestrial Physics 70（2008）774-793.

［12］Bowman，B.R..A New Empirical Thermospheric Density Model JB2008 Using New Solar and Geomagnetic Indices，AIAA/AAS Astrodynamics Specialist Conference 18-21 August 2008，Honolulu，Hawaii

［13］Tobiska，W.K..Forecast E10.7 for Improved LEO Satellite Operations，American Institute of Aeronautics and Astronautics，2002