京新高速上地斜拉橋抗震設計分析

辛 兵 王克海 徐升橋

(1.中鐵工程設計咨詢集團有限公司，北京 100055;2.交通運輸部公路科學研究所，北京 100088)

斜拉橋由于跨越能力大，造型優美流暢，布局較容易與周圍環境相協調統一，近年來在城市橋梁建設中被廣泛采用。斜拉橋既能滿足結構要求，又具有景觀效果，往往成為城市具有標志性的建筑。大跨徑斜拉橋作為城市交通路線上的樞紐工程和生命線工程，若遭受地震災害破壞，無論重建還是改線繞行都較為困難，并影響救災工作的順利進行，造成重大的經濟損失。因此，對大跨徑斜拉橋進行合理、有效的抗震設計，以確保其在大震中的安全性，具有十分重要的社會和經濟意義。

1 工程概況

京包高速公路工程上地鐵路分離式立交公路大橋位于京包高速公路(北京市五環路—六環路)上，本橋采用(46+46+230+98+90)m五跨連續獨塔單索面預應力混凝土半漂浮體系斜拉橋，全橋長510m。主塔為倒Y形塔，采用塔、墩固結體系，主梁支承于塔墩上，塔高99m，索塔高度與中跨比為0.38，主梁主跨的跨高比為1/68(如圖1所示)。

本橋需跨越城鐵13號線、既有京包鐵路以及京張城際鐵路，抗震安全問題顯得尤為重要。根據《中國地震參數區劃圖》(GB 18306—2001)，本區地震動峰值加速度為0.20g，地震基本烈度為Ⅷ度，按Ⅸ度設防。按照現行《公路橋梁抗震設計細則》(JTG/TB02—01—2008)，其抗震設防類別為A類，抗震設防目標既要保證橋梁的抗震安全性，又不致使造價增加太多，需要在經濟性與安全性之間進行合理平衡，這是橋梁抗震設防的合理原則。

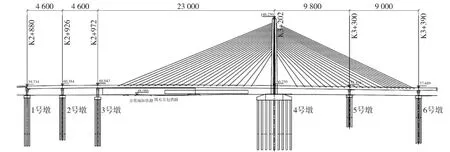
圖1 全橋結構形式(單位:cm)

根據本橋橋梁結構各部分的重要性，以及地震破壞后橋梁結構的性能要求、修復(搶修)的難易程度，主橋采用50年超越概率10%(E1)、2%(E2)地震作用輸入作為設防標準，見表1。

表1 橋梁抗震校核準則

2 全橋空間有限元模型

采用MIDAS有限元程序，建立三維有限元動力計算模型進行抗震性能分析，計算模型均以順橋向為X軸，橫橋向為Y軸，豎向為Z軸;主梁采用單梁模擬，拉索采用桁架單元模擬，主塔采用三維梁單元模擬，承臺按梁單元模擬;進入土體的樁基礎部分考慮樁—土—結構相互作用，采用六自由度土彈簧進行模擬，土彈簧剛度采用“m”法確定(如圖2所示)。

本橋在所有橋墩墩頂及橋塔處分別設置了縱向或多向活動盆式橡膠支座，根據《公路橋梁抗震設計細則》(JTG/T B02—01—2008)，有限元建模時應考慮活動盆式支座的影響，活動盆式支座可用雙線性理想彈塑性彈簧單元模擬，其初始剛度k按下式計算

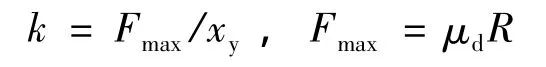
式中，μd為滑動摩擦系數，一般取0.02;R為支座承擔的上部結構重力;xy為活動盆式支座屈服位移，一般取0.002～0.005m。

圖2 斜拉橋動力計算有限元模型示意

3 自由振動特性分析

分析和認識橋梁的動力特性是進行橋梁抗震性能分析的基礎。在小震作用下考慮盆式支座水平摩擦力提供的初始剛度，對本橋(模型一)進行模態分析得到全橋前100階周期與振型，取前10階模態的頻率與振型，如表2所示，前4階振型圖如圖3～圖6所示。在大震作用下主梁與盆式支座在活動方向發生滑動，支座不能提供水平剛度約束，按不考慮支座的影響(模型二)對本橋進行模態分析得到全橋前100階周期與振型，取前10階模態的頻率與振型，如表2所示，前4階振型圖如圖3～圖6所示。

從以上斜拉橋自振特性分析可知，對于模型一，考慮盆式支座的影響，在振動時對主梁提供水平約束，因此表現出斜拉橋的第1階模態為主梁的豎向彎曲振型，第2階振型才出現全橋縱漂振型，表明斜拉橋全橋豎向剛度小于縱向剛度;第3階仍為主梁的豎向振動振型，第4階為主梁反對稱側彎振型，第9階為主塔側彎振型，說明斜拉橋橋塔橫橋向剛度大，對抵抗地震動作用非常有利。對于模型二，是基于大震作用下，盆式支座在活動方向主梁與支座發生相對滑動，支座不能提供水平約束，縱向剛度小于全橋的豎向和橫向剛度，其第1階模態表現為全橋縱漂振型，第2階模態為主梁豎彎振型，第3階模態為主梁側彎振型，表明主梁橫向剛度大于豎向剛度;第7階模態出現橋塔的側彎振型，表明橋塔橫向剛度大。

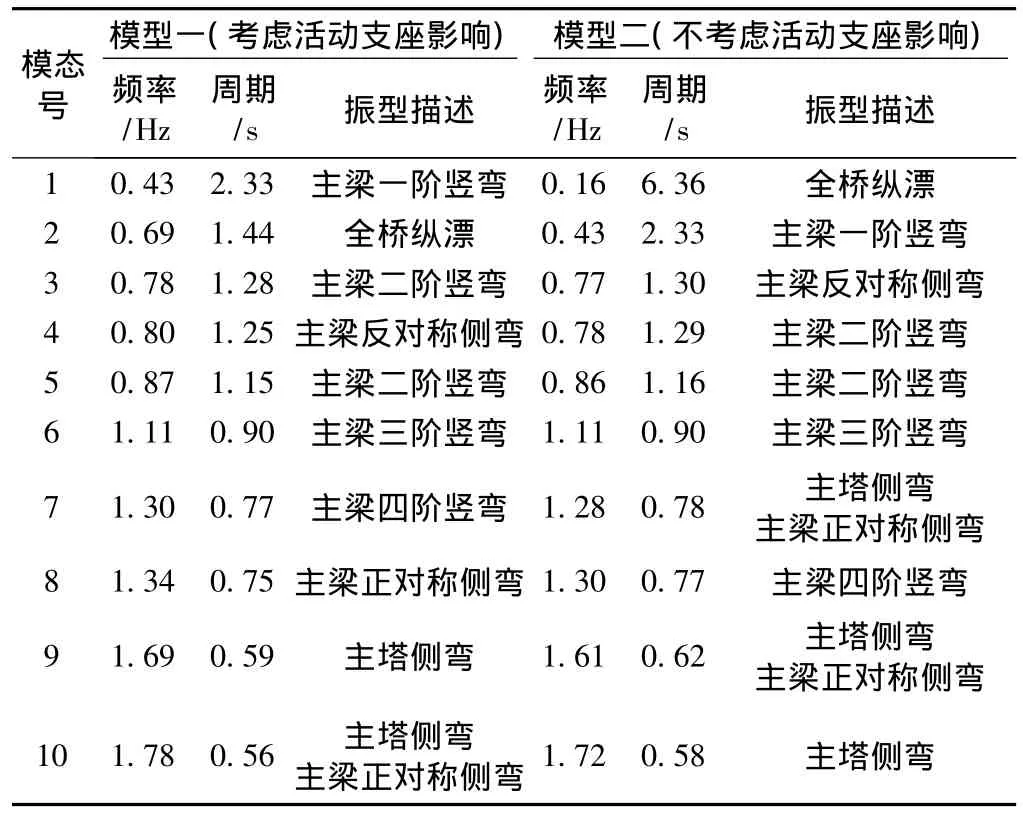
表2 前10階頻率及振型

圖3 主梁一階豎彎(模型一第1階模態、模型二第2階模態)

圖4 全橋縱漂(模型一第2階模態、模型二第1階模態)

圖5 主梁二階豎彎(模型一第3階模態、模型二第4階模態)

圖6 主梁反對稱側彎(模型一第4階模態、模型二第3階模態)

4 反應譜分析

4.1 反應譜輸入

反應譜理論也稱動力法，是目前世界各國應用最為廣泛的抗震分析方法，其優點是考慮了地震時地面的運動特性與結構物自身的動力特性，計算量少，且加速度反應譜值是加速度反應的最大值，用它來控制設計一般是安全的。

本橋位處地震基本烈度為Ⅷ度，按Ⅸ度設防，地震動峰值加速度為0.20g，E1地震作用下水平設計加速度反應譜最大值Smax=0.45g，E2地震作用下水平設計加速度反應譜最大值Smax=0.765g，對于豎向地震系數取水平向的0.67倍(如圖7所示)。

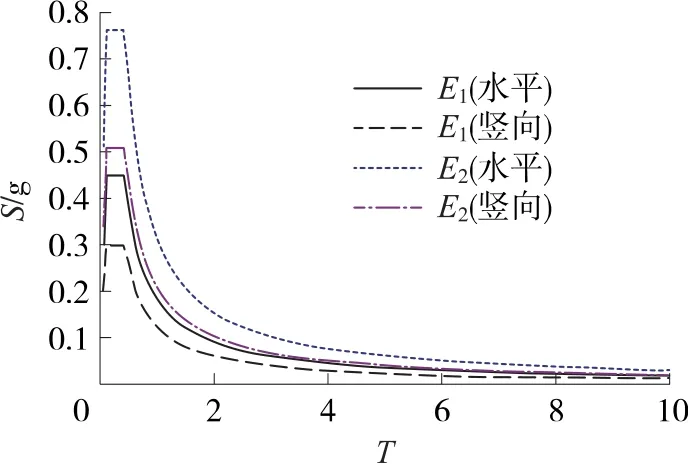
圖7 反應譜

采用多振型反應譜法計算，所考慮的振型階數應在計算方向獲得90%以上的有效質量。本文計算了前100階自振周期和振型參與系數，其累積振型參與質量見表3，其中順橋向X、橫橋向Y，豎向Z。

表3 累積振型參與質量_

從表3中數據可知，各振動方向在第100階模態的累積振型參與質量到達95%以上，滿足反應譜分析模態數量的要求。結構的振型組合采用CQC法，同時考慮順橋向X、橫橋向Y與豎向Z的地震作用，方向組合采用SRSS法。

4.2 計算結果分析

(1)模型一(考慮活動支座的影響)

本斜拉橋在地震作用下驗算的關鍵截面主要是兩側橋塔根部和邊跨各橋墩墩底截面，以及驗算盆式支座的位移和水平承載力(如表4、表5、表6所示)。

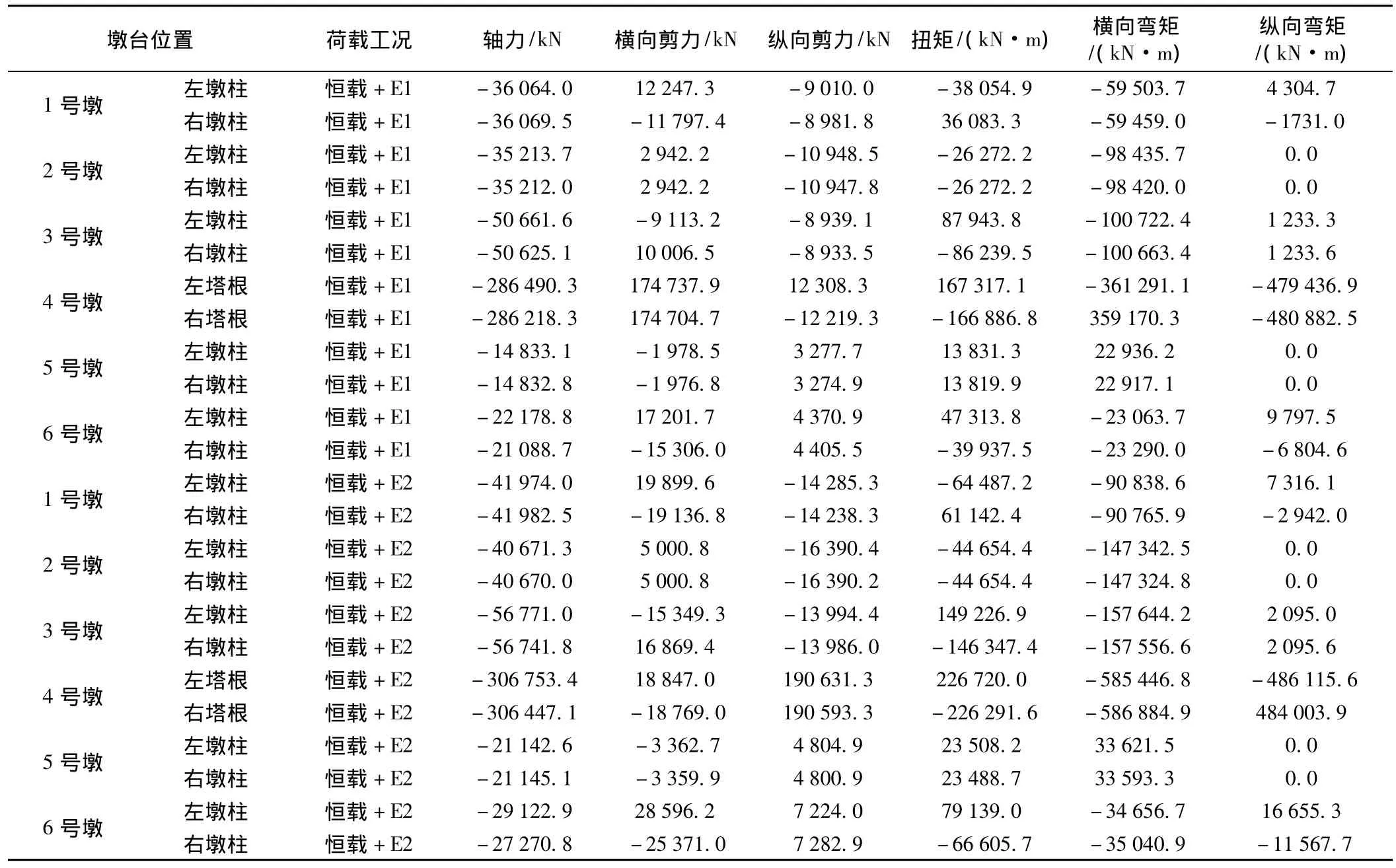
表4 關鍵截面內力(模型一)

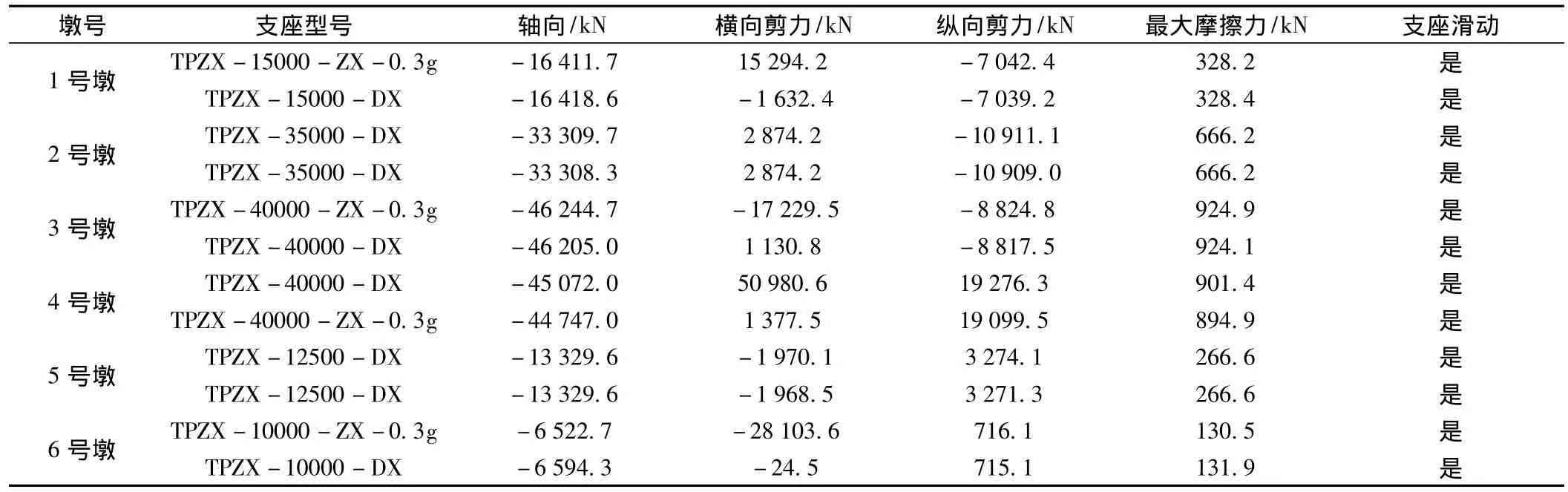
表5 恒載+E1地震作用下支座反力(模型一)

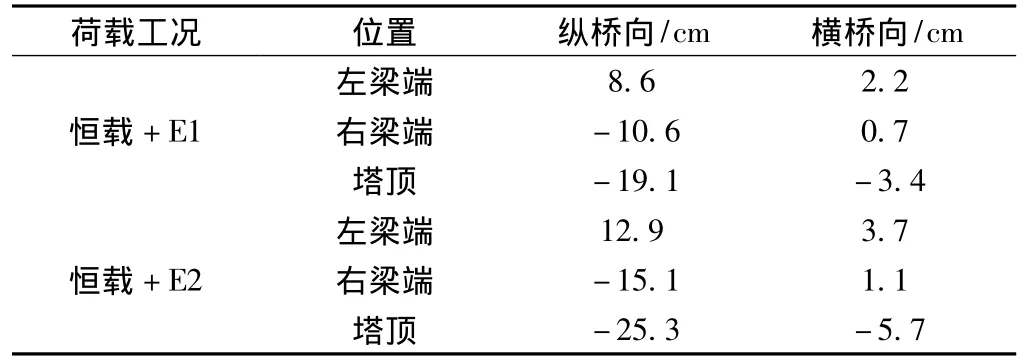
表6 地震作用下梁端及塔頂位移

從表5可知，在E1地震作用下，盆式支座的活動方向所受的水平力大于支座能提供的最大靜摩擦力，主梁體與支座在活動方向發生相對滑動，因此在E1地震作用下不應考慮盆式支座的水平剛度影響。

(2)模型二(不考慮活動支座的影響)

不考慮盆式支座活動方向的水平剛度影響，重新計算全橋結構關鍵截面內力，計算結果如表7～表9所示。

(3)計算結果分析

通過對比模型一和模型二的模態分析和反應譜計算結果，可以看出:

①模型一的剛度比模型二大，因此其基頻比模型大，對應于相同的反應譜函數，模型一所受到的地震加速度大于模型二。

②考慮盆式支座活動方向主梁與支座之間靜摩擦影響所產生的水平剛度，將增大全橋結構縱向剛度，導致大跨柔性的斜拉橋體系第一階模態表現為主梁豎彎振型，其次是由縱向剛度引起的縱漂振型。模型二的結構縱向剛度完全由主塔提供，其剛度一般小于全橋豎向和橫向剛度，表現出第一階模態為縱漂振型，其次是主梁豎向彎曲振型。

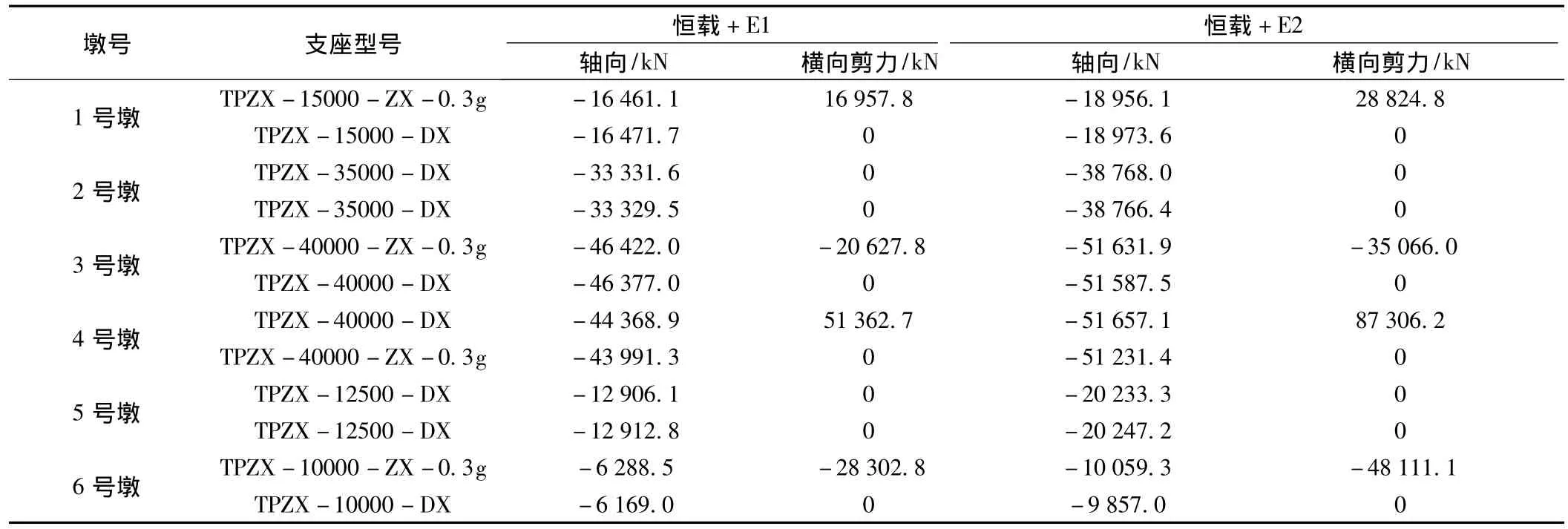
表8 地震作用下支座反力(模型二)

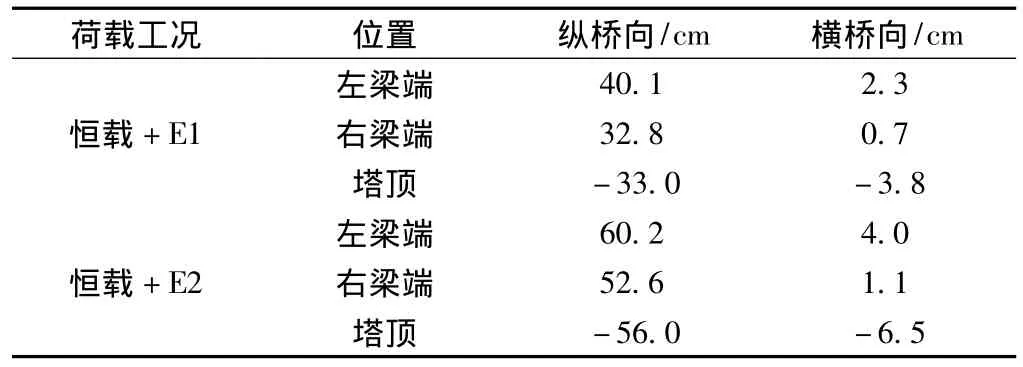
表9 地震作用下梁端及塔頂位移(模型二)

③模型一在地震作用下，由于考慮了盆式支座的影響，在支座活動方向將有水平力通過支座傳遞到下部結構，引起墩底相應方向的水平力和彎矩;而模型二不考慮支座活動方向剛度的約束，其墩底剪力和彎矩比模型一小。對于橋塔結構兩側的根部截面，由于縱向活動支座不分擔由地震荷載引起的水平力，因此模型二在該截面處的縱橋向剪力和彎矩均大于模型一。

④地震作用下支座的水平反力，模型一在支座縱向活動方向承擔了部分水平力，減小了主塔的縱向受力，在橫向活動方向支座的水平剛度減小了橫向固定的盆式支座水平剪力，有利于保護橫向固定支座不被剪壞;模型二的縱向水平力全部由橋塔承受，橫向水平力則由橫向固定支座及橋塔承受。

⑤大跨度斜拉橋在地震作用下的梁端及塔頂位移，橫向位移基本相同，而對于縱向位移，不考慮支座影響的模型二的位移量是考慮支座影響的模型一的位移量的3倍。

⑥在E1地震動作用下，采用彈簧單元模擬的盆式支座活動方向臨界滑動摩擦力Fmax=μdR的計算結果小于彈簧單元的水平剪力，表明主梁與盆式支座活動方向發生相對滑動，因此活動盆式支座不能采用規范推薦的雙線性理想彈塑性彈簧單元來模擬，即在E1地震作用下應不考慮支座的影響來建立全橋模型模擬在地震作用下的反應譜響應。

5 結束語

(1)考慮活動支座影響的斜拉橋模型比不考慮活動支座影響的模型基本振動周期短、剛度大，兩模型之間前4階自振模態變化大，第5階之后的振型基本相同。

(2)考慮地震作用下支座的影響，能夠減小盆式支座固定方向的水平力，也能減小橋塔根部截面的剪力和彎矩，但增加了其他橋墩墩底的內力。因此在設計時應平衡考慮上部結構和下部結構之間的受力關系，在確保橋墩地震安全的前提下合理選用和布置支座，盡量減小橋塔的受力，保證主塔在大震作用下發生局部輕微損傷或不發生損傷。

(3)在小震作用下，盆式支座在活動方向受到的水平力小于臨界滑動摩擦力，則需要考慮活動支座對全橋結構的影響。在大震甚至設計地震時，盆式支座的活動方向受到的水平力大于臨界滑動摩擦力，應將支座活動方向的剛度完全釋放。

(4)不考慮支座影響的斜拉橋結構，在地震作用下以縱漂振型為主，導致全橋縱向位移較大，需要采取相應的措施來減小全橋的縱向位移，防止主梁與附近橋跨發生碰撞損壞。

［1］王克海．橋梁抗震研究［M］．北京:中國鐵道出版社，2006

［2］鄒立華，王克海，趙人達．大跨RC斜拉橋的非線性地震響應分析［J］．鐵道學報，2004，26(6):95 －99

［3］王克海，朱晞．斜拉橋基于模態分析的滑動狀態減震控制研究［J］．橋梁建設，2001，6:1 －4

［4］范立礎．橋梁抗震［M］．上海:同濟大學出版社，1997

［5］孫利民，張晨南，潘龍，等．橋梁樁土相互作用的集中質量模型及參數確定［J］．同濟大學學報，2002，30(4):409 －415

［6］戴鵬，郝憲武，狄謹．大跨徑P斜拉橋地震響應非線性分析［J］．鄭州大學學報(工學版)，2006，27(4):79 －83

［7］葉愛君，胡世德，范立礎．斜拉橋抗震結構體系研究［J］．橋梁建設，2002(4):1－4