風力發電機組輪轂高應力區抗拉強度特性評估

魏錚 上海電氣集團股份有限公司中央研究院 (200270）張天明 上海電氣風電設備公司 (200241）

蔣毓良 上海宏鋼電站設備鑄鍛有限公司 (2002400）

0 引言

風力發電機組中的輪轂系球墨鑄鐵件，它將三個葉片所受的風載荷傳遞給主軸。風載荷是一種非穩定載荷，輪轂的受力狀況比較復雜。按有關風機輪轂設計規范規定，風機輪轂除作靜態強度計算外，還需作動態強度(即疲勞強度)計算，而輪轂材料的抗拉強度是輪轂靜態強度和疲勞強度計算的重要計算依據，因此，輪轂材料的抗拉強度被認為是一個重要的材料特性值。

由于輪轂形狀復雜，幾何尺寸大，輪轂各部位壁厚也不盡相同，以及球墨鑄鐵件的致密性等原因，若從輪轂本體不同部位上截取多個樣品作抗拉強度試驗，其試驗值會在一定的范圍內波動而呈離散分布，很難用某個樣品實測的試驗數據較客觀地描述出輪轂本體的抗拉強度特性。為此，須研究輪轂本體的抗拉強度離散分布規律后，才能評估輪轂本體抗拉強度特性。評估工作應首先在輪轂本體不同部位上隨機截取一定數量的樣品，并對樣品作抗拉強度性能測試，然后用數理統計方法，研究和確定樣品的全部抗拉強度測試值之間的關系和參數，按一定的數學模型，把這些樣品實測值轉化成可評估輪轂樣品的數學公式或圖表。當樣品是在輪轂本體不同部位上獲取時，樣品的抗拉強度特性就代表了輪轂本體的抗拉強度特性，對輪轂樣品的評估，就代表了對輪轂本體的評估，因此，這些用于評估輪轂樣品的數學公式或圖表可用于評估輪轂本體的抗拉強度特性。

1 輪轂樣品和抗拉強度性能測試

為了能夠充分的了解輪轂本體各項性能和對輪轂制造工藝的驗證，特意鑄造了2MW風機輪轂一個。輪轂壁厚在40～130mm之間，重量大約10t。輪轂設置了40、70、100mm厚度的附鑄試塊各1塊（見圖1），按國家風電標準規定，40mm和70mm附鑄試塊性能分別代表壁厚在30～60mm和60～200mm之間的球墨鑄鐵件的本體性能，100mm附鑄試塊為項目科研用。然后對輪轂作全面解剖，在輪轂不同部位上截取了多個樣品，分別對這些樣品作拉伸強度、沖擊韌性和微觀組織等方面的測試，得到了大量的測試數據。

圖1 2MW風機輪轂及附鑄試塊布置

其中高應力區輪轂樣品（壁厚在60～120mm之間）抗拉強度測試值（以下簡稱樣品值）列于表1（未將壁厚在40～60mm之間的樣品值列在該表中），樣品值代表了高應力區且壁厚在60～120mm之間的輪轂本體的抗拉強度特性。從輪轂本體不同部位取出樣品并對樣品作抗拉強度性能測試是評估輪轂高應力區抗拉強度特性的第一步基礎工作。

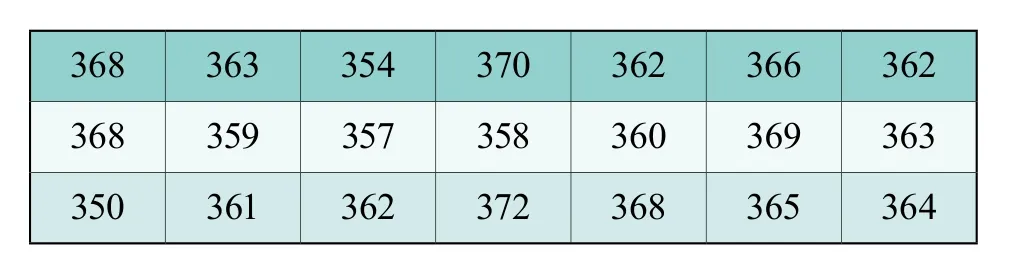
表1 輪轂高應力區樣品抗拉強度實測值（MPa）

從表1可知，從輪轂高應力區上截取的樣品上共得到21個抗拉強度測試數據，其中最大值為372 MPa，最小值為350 MPa，它們的算術平均值為363 MPa。另外，根據國家有關風電標準規定，用附鑄試塊性能代表球墨鑄鐵件性能，為了研究需要，在該輪轂上設置40、70、100mm厚度的附鑄試塊各1塊，其中70mm厚度的附鑄試塊的抗拉強度實測值為380MPa，高于表1列出的所有樣品值，試驗結果表明輪轂本體的抗拉強度將低于附鑄試塊的抗拉強度。

2 輪轂樣品抗拉強度評估步驟

2.1 樣品值分級

表1提供的樣品抗拉強度測試數量（以下稱樣品數量）有21個，將21個樣品值從小到大排序后，可知樣品抗拉強度最大值為372 MPa，最小值為350 MPa。取樣品區間為[349，373]，則樣品值區間的長度為373～349=24。將樣品區間分為6個小區間，每個樣品值分級區間為24/6=4 MPa。統計在各分級區間內出現的樣品值和樣品值個數，統計結果見表2。

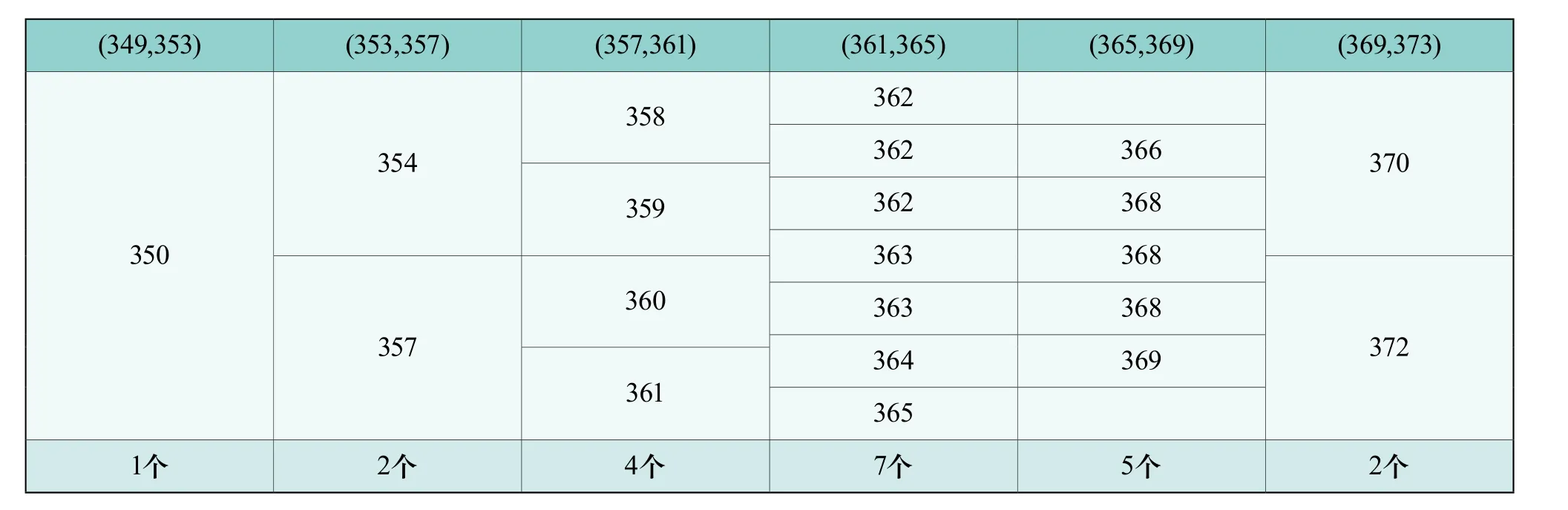
表2 樣品分級區間和樣品值個數

2.2 確定分級頻次，計算分級頻率

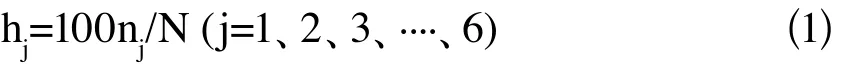
計算每個樣品分級區間中的分級頻率后，得到不同區間內的分級頻次和分級頻率的關系表，見表3。

表3 樣品分級區間分級頻次和分級頻率

2.3 離散樣品頻率分布圖

依據表3的數據，用直方圖表示各樣品分級區間中的分級頻次nj與分級頻率hj的關系見圖2（縱軸為的值，橫軸為樣品分級區間），所有的直方圖構成了一個階梯圖，該階梯圖稱為離散樣品頻率分布圖。該階梯圖表示出輪轂樣品在各分級區間內抗拉強度值的分布頻率。每個直方圖中的矩形面積表示出占階梯圖總面積的比例（用hj值表示）。從圖2可看出，離散樣品頻率呈“中間大，兩頭小”，近似于鐘型分布的特點。

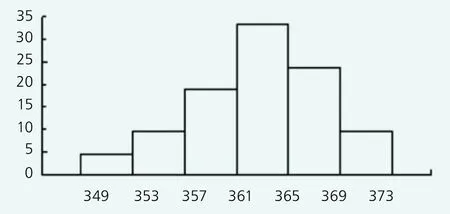
圖2 離散樣品頻率分布

2.4 確定累加分級頻次，計算累加分級頻率

部分分級頻率之和定義為累加分級頻率，累加分級頻率描述了樣品值在j分級頻次范圍以下的總頻率分布情況。

累加分級頻次計算公式為：

由表3可得，N1=n1=1，N2=n1+n2=1+2=3，N3=n1+n2+n3=1+2+4=7，其余可依次類推。

累加分級頻率的計算公式為：

由式3可得到：h1=N1/N=1/21=4.76%，h2=3/21=14.28%，其余可依次類推。

6個樣品分級區間內累加分級頻次與累加分級頻率的關系見表4。

表4 樣品分級區間內累加分級頻次與累加分級頻率

2.5 離散樣品累加頻率分布

為能較直觀地表示累加分級頻次與累加分級頻率的關系，可根據表4的數據，繪制出輪轂離散樣品累加頻率分布，見圖3。圖3回答了在j分級頻次范圍以下出現的頻率，如樣品值小于等于365MPa的頻率為66.64%。

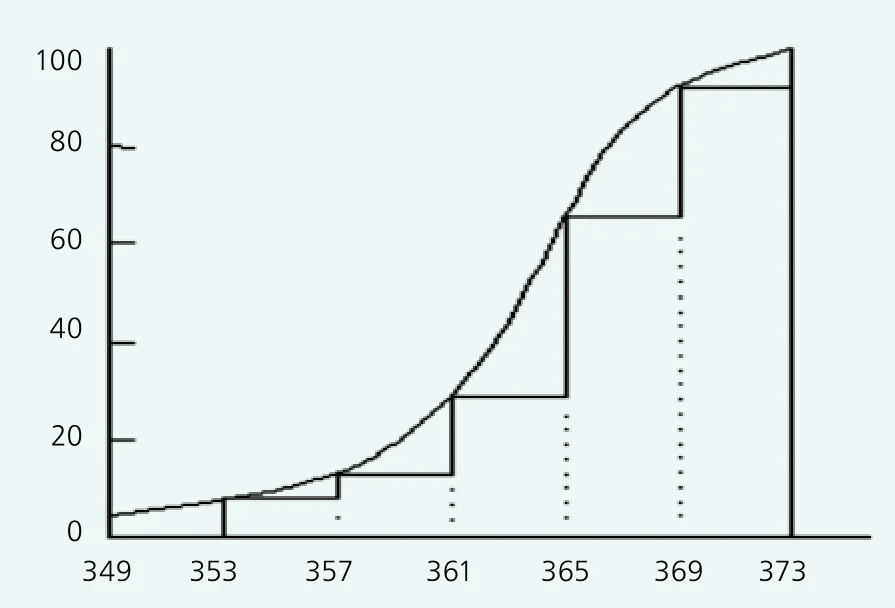
圖3 輪轂離散樣品累加頻率分布

2.6 概率密度函數

圖2 所示的離散樣品頻率分布（即階梯圖）確定了輪轂樣品值頻率分布情況，樣品值頻率呈鐘型分布態勢。在評估樣品抗拉強度特性時，需要根據離散樣品頻率分布圖建立一個數學模型，用一個連續的概率密度函數來代替輪轂離散樣品的頻率分布，該函數可指出，當在輪轂本體高應力區上重新取樣作抗拉強度試驗時，所有的樣品值將服從的概率分布。可選用的概率密度數學模型有許多種，而呈鐘型分布態勢的概率密度函數f（x）通常是正態分布的概率密度函數。已知正態分布概率密度函數的一般公式為

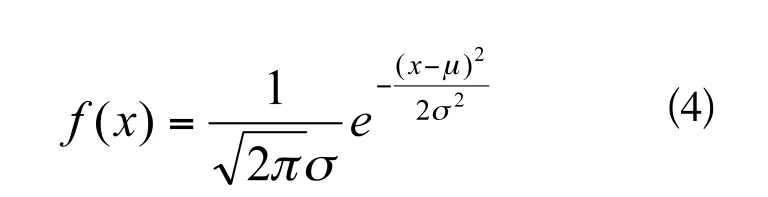
其中μ，σ為待定參數，若求得μ，σ，便可以求得f(x)。取μ為樣品的算術平均值，σ2為樣品的方差，σ為樣品的標準差，則μ，σ2按如下公式計算：

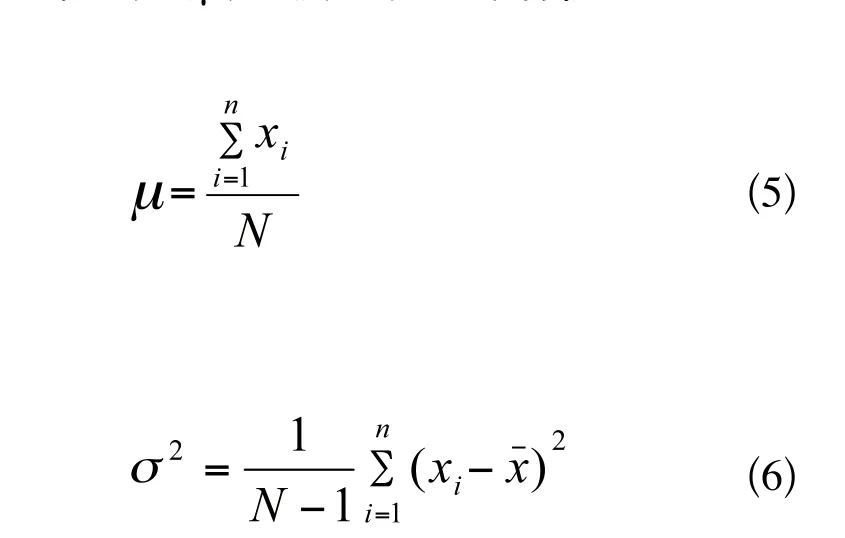
將表1中的每個樣品值作出標記列于表5，計算樣品的算術平均值μ、方差σ2和標準差σ：

表5 給輪轂樣品值作出標記

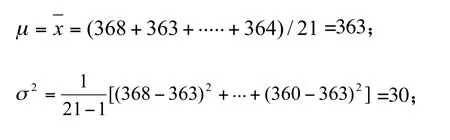
σ=5.5,

代入式4，輪轂樣品的概率密度函數f(x)為：

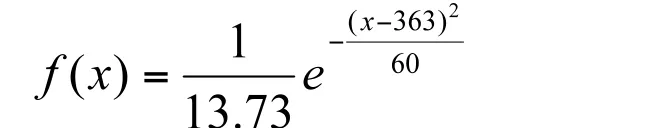
f(x)函數的曲線圖如圖4所示，它用連續的樣品概率分布曲線代替了離散樣品頻率分布階梯圖，并由此可推斷出所有在輪轂高應力區上的樣品值概率密度情況。

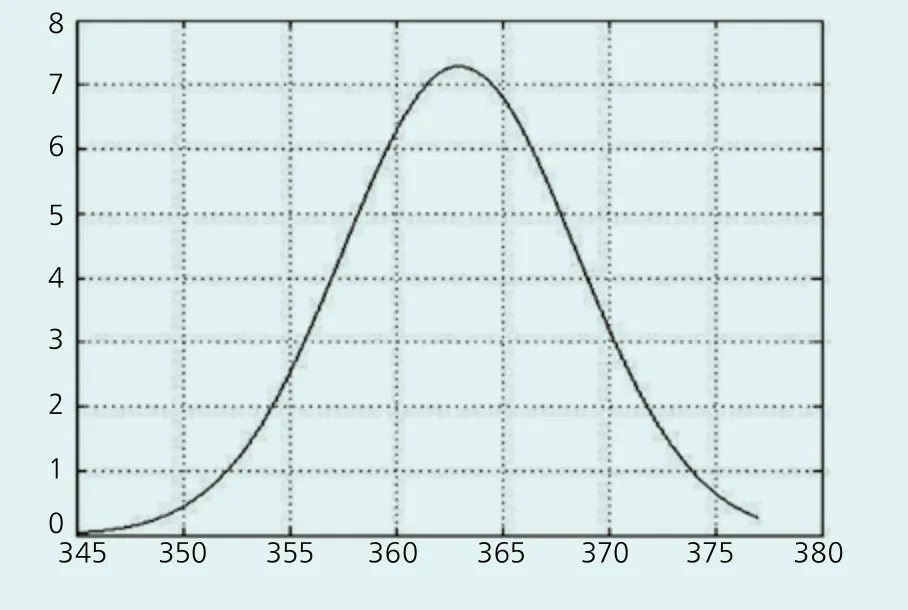
圖4 輪轂樣品連續概率密度函數曲線

2.7 樣品分布概率函數和穿越概率函數

已知輪轂樣品連續概率密度函數則樣品在 [a,b] 區域內的分布概率函數

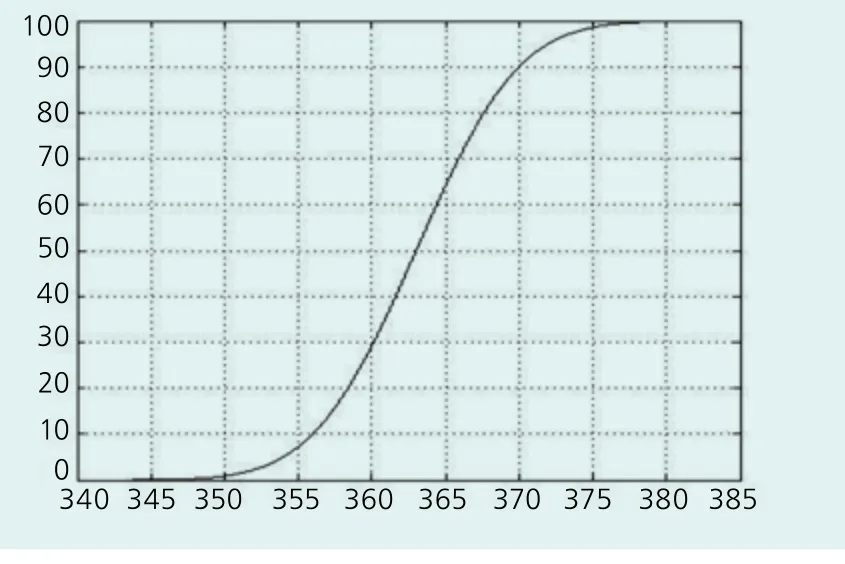
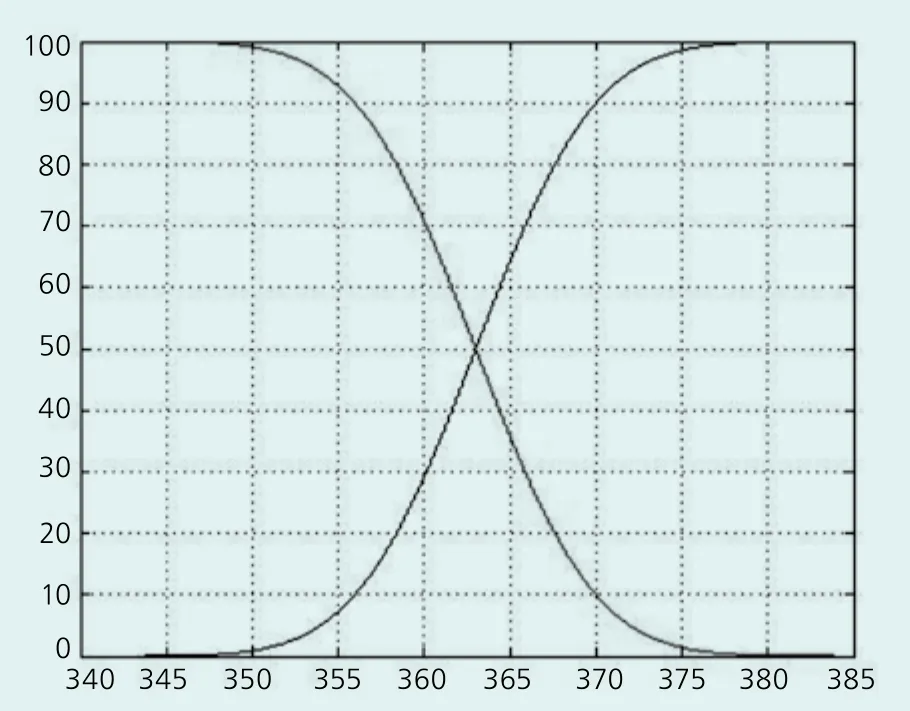
如圖5所示，在a至b區域內，樣品分布概率函數F（x）是f(x)曲線與x軸構成的面積，它表示了樣品值在a至b區域內的分布概率，其中0

圖5 輪轂樣品抗拉強度分布概率曲線

樣品分布概率函數F（x）需要對進行積分才能求解，而* MERGEFORMAT沒有解析解，通常用Malab軟件，對其進行數值積分求解，然后根據這些數值，擬合成一條輪轂樣品分布概率曲線，輪轂樣品分布概率曲線如圖5所示。

圖5 輪轂樣品抗拉強度分布概率曲線

輪轂樣品分布概率函數F（x）或輪轂樣品分布概率曲線圖反映了凡從輪轂本體上取出的樣品作抗拉強度試驗，樣品值小于某個值的概率，即所有取自于輪轂本體的樣品值分布規律將服從輪轂樣品分布概率函數F（x）或輪轂樣品分布概率曲線圖所指出的分布概率。

若令Fu(x)=1-F(x)，則Fu(x)反映出所有取自于輪轂本體的樣品值大于某個值的概率，它被稱為輪轂樣品穿越概率函數。根據輪轂樣品分布概率函數F（x）和穿越概率函數Fu(x)擬合的曲線見圖6。

輪轂樣品分布概率函數F（x）和輪轂樣品分布概率曲線圖或輪轂樣品穿越概率函數Fu(x)和穿越概率曲線圖是工程上評估該輪轂抗拉強度水平的數學公式和圖表。如由圖6可很容易地推斷出該輪轂抗拉強度小于等于370MPa的概率為90%（分布概率），或≥370MPa的概率為1-90%=10%（穿越概率）；輪轂本體抗拉強度出現在363MPa(輪轂樣品平均值)和370MPa之間的概率為90%-50%=40%。

圖6 F(x)與Fu(x)擬合曲線圖

3 輪轂本體高應力區抗拉強度評估

根據圖5或圖6所示概率分布曲線，可對輪轂本體高應力區的抗拉強度進行如下評估：

(1)以平均值μ為中軸，在正負標準差σ范圍內，輪轂本體的抗拉強度值出現在357～368 MPa范圍內的概率為 68.72 %。

(2)輪轂本體抗拉強度值在分布概率為10%以下時，在工程上可認為是小概率事件。根據圖6，可得到其分布概率為2.5%，5%和10%時所對應的抗拉強度值分別為352.3MPa、354MPa和356MPa，這意味著，輪轂本體抗拉強度值達到352.3MPa、354MPa和356MPa時的可信度為97.5%、95%和90%。因此，從輪轂件安全性和經濟性考慮，可選用不同小概率所對應的抗拉強度值作為精確設計計算的起算值；另外，它也可以作為供需雙方確定輪轂本體抗拉強度考核指標的依據。

(3)輪轂本體抗拉強度值在分布概率為90%以上（或穿越概率在10%以下）時，在工程上也認為是小概率事件。根據圖6，計算出穿越概率為2.5%、5%和10%時所對應的抗拉強度值分別為373.8MPa、372MPa和370MPa。因此，輪轂70mm附鑄試塊實測的380MPa抗拉強度值在輪轂本體上屬于不可能發生的事件，換言之，輪轂在壁厚為60～120mm范圍內的高應力區的樣品值將低于附鑄試塊抗拉強度實測值，甚至低于球墨鑄鐵材料名義值（370MPa）。所以，附鑄試塊抗拉強度不可籠統地認為能代表輪轂本體的抗拉強度。在穿越概率為2.5%時，即在可信度為97.5%時，輪轂本體的抗拉強度僅為附鑄試塊抗拉強度的92%，為輪轂球墨鑄鐵材料的名義抗拉強度值的95%。

其他試驗結果表明，輪轂在壁厚為30～60mm范圍內的高應力區的樣品值與40mm附鑄試塊抗拉強度實測值相當，因此，40mm附鑄試塊抗拉強度實測值可代表輪轂本體抗拉強度特性。

4 結語

從大型球墨鑄鐵件不同部位取出樣品，樣品的抗拉強度測試值通常是在一定的范圍內波動，當樣品值呈離散分布時，可通過用一個特定的數學公式或相關的圖表來描述大型球墨鑄鐵件樣品值的分布概率，以此來評估該球墨鑄鐵件的抗拉強度特性。

制作一個大型球墨鑄鐵件是開展評估工作的最基本的條件，從大型球墨鑄鐵件隨機抽樣并得到一定數量的測試數據是評估工作的前提條件，在上海市科委的資助下，通過開展有關科研項目，使以上二個條件均得到了滿足，才使輪轂抗拉強度特性的評估工作得以順利開展成為可能，在此，特向上海市科委對項目的資助表示感謝！

GB/T25390-2010 風力發電機組 球墨鑄鐵件

Guideline for the Certification of Wind Turbines(Edition 2010)

德國鋼鐵工程師協會，工作強度計算手冊——推薦用于機械結構件壽命評估（第四版）