一般化通用可組合安全框架研究

張 妤，彭 亮

（1.解放軍信息工程大學 電子技術學院，河南 鄭州450004；2.63850部隊，吉林 白城137001）

0 引 言

Ran Canetti 2001年提出的通用可組合安全框架［1］（UC框架）是用組合方法分析密碼協議的成功范例，也是近年來密碼協議分析領域的研究熱點。國內外對于UC框架的研究主要是針對特定密碼學任務提出具有UC安全性的協議方案，如UC安全的零知識證明［2］、不經意傳輸［3］、簽密［4］、安全多方計算［5］、數字簽名［6］、認證及 密鑰交換［7－9］等。UC框架擔保的任意組合及并發執行時的安全性雖然在最大程度上滿足了人們的安全需求，但也正因為如此高的要求使得大部分UC安全協議的存在性需要一個全局可信的建立階段。為了使UC框架更加適應全局可信建立，Canetti于2007年提出了一般化通用可組合安全框架［10］（GUC框架）。目前對GUC框架的研究剛剛起步，姚期智先生對GUC框架的可行性進行了相關研究［11］。受此啟發，本文沿著UC框架到GUC框架的發展脈絡，首先對提出GUC框架的本質原因 （GUC框架解決的關鍵問題）進行深入分析，然后研究了GUC框架的機理和可實現性，并將GUC框架與UC框架及其改進版本進行了比較，最后討論了GUC框架仍然存在的問題。

1 GUC框架解決的關鍵問題分析

UC框架使用基于仿真的證明方法：如果對于攻擊現實協議π（由通信方P1和P2執行）的任何PPT敵手A，都存在攻擊理想協議 （由虛通信方P’1和P’2調用理想功能F來執行）的PPT仿真器S，使得無論PPT環境Z使用任何協議輸入作為測試，π和 的輸出都是計算上不可區分的。則πUC－仿真了 ，或者說π具有F要求的UC安全性。公鑰加密、數字簽名、密鑰交換等原語在樸素模型中是可以UC安全實現的［1］。圖1給出了樸素模型中的UC仿真示意圖。

圖1 樸素模型中的UC仿真

然而在樸素模型中絕大多數安全計算 （現實中有意義的安全計算）不能被UC安全實現［12］。考慮一個UC安全的兩方安全計算協議，如果通信方之一P1與環境串通，則環境Z可以代替通信方P1來執行P1的協議程序與誠實通信方P2照常完成協議 （由敵手A中轉雙方的消息）。這種情況下，一方面，安全計算的秘密性要求沒有PPT算法能夠提取誠實方P2的輸入，并且除了環境之外沒有PPT算法能夠提取P1的輸入。另一方面，UC安全性要求存在PPT仿真器S使得理想協議也能被完成。現在就出現問題了：完成理想協議時P1的輸入是由S轉交給F的，則S一定可以從P1的發送消息中提取P1的輸入，即除了環境之外還存在PPT算法能夠提取P1的輸入。可見，UC安全計算既要求安全計算的秘密性，又要求通用可組合性，而通過上面的分析這兩個要求是矛盾的。這正是在樸素模型中有意義的安全計算不能被UC安全實現的根本原因。

文獻 ［13－14］展示了假定存在一個全局可信建立階段，可以使得UC安全計算存在。UC框架將所需要的全局可信建立假定抽象為特定的理想功能M，使用這些假定的協議被描述為可以訪問M的混合協議，其UC仿真示意圖如圖2所示。在現實協議中M的程序由一個可信方來執行（文獻 ［14］的防篡改硬件令牌是可信方的另一種抽象，只不過無論對于多么可信的可信方，人們都害怕他有失信的時候；而對于防篡改硬件令牌卻不會擔心它會變為可篡改的），在理想協議中在需要M的時候由仿真器來執行。在UC安全計算方案中使用陷門函數，執行M的過程中可以生成陷門信息。由于現實世界的可信方并不泄露該陷門信息，所以可以實現安全計算；由于理想世界的仿真器知道該陷門信息，所以可以實現UC仿真。綜合這兩方面的結果是，在全局可信建立混合模型中安全計算可以被UC安全實現了。

圖2 使用全局可信建立M的UC仿真

但是事情并沒有就此結束。按照仿真證明方法的本意，若理想協議具有某個性質，則仿真該理想協議的現實協議也應該具有。然而當使用全局建立的時候 （比如文獻 ［13］中的公共參考串CRS），這種情況不再成立：存在這樣的協議π［15］，它UC仿真了一個具有可否認性的理想協議，然而π卻不具有可否認性 （說一個協議是可否認的是指，協議參與者可以否認他們參與了一個協議會話，通過爭辯說他們參與的任何證據都可以被偽造）。GUC框架要解決的關鍵問題就是使得UC框架更好地處理全局可信建立，使得仿真證明方法的本意得以保持，即仿真成功擔保現實協議具有理想協議的所有性質 （稱此為完全可仿真性）。

2 GUC框架研究

2.1 GUC框架機理研究

當不使用全局可信建立的時候，GUC框架與UC框架（確切地說是JUC框架）是一樣的，GUC框架對UC框架的改進在于使用全局可用建立的時候。此時，GUC框架使環境Z也可以訪問建模全局可信建立的理想功能M。由于Z可以直接訪問真正的M，仿真器S就不能用仿真的M來應對Z，因此GUC框架要求使用全局可信建立時的成功仿真由仿真器調用真正的M來完成，其GUC仿真示意圖如圖3所示。

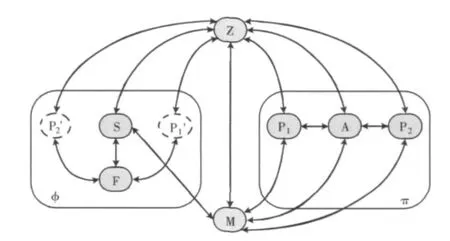
圖3 使用全局可信建立M的GUC仿真

我們來研究GUC框架既保證通用可組合安全計算的可實現性、又保證完全可仿真性的機理。在UC框架樸素模型中實現不了通用可組合的安全計算，本質原因通用可組合性的要求和安全計算的要求是矛盾的，而在仿真器與現實敵手擁有同樣的能力時這個矛盾是無法解決的；UC框架使用全局可信建立時候，雖然通用可組合性要求和安全計算要求的矛盾仍然存在，但是通過讓仿真器擁有比現實敵手更強的能力 （可以使用仿真的M），這個矛盾是可以解決的，因此通用可組合的安全計算得以實現。可見樸素模型中要求仿真器在與現實協議同樣的基礎上UC仿真成功，使用全局可信建立的混合模型中要求仿真器在比現實協議更高的基礎上UC仿真成功，這實際上是全局可信建立的使用降低了通用可組合性要求使得通用可組合的安全計算得以實現，這個要求的降低使得使用全局可信建立的UC安全的協議喪失了完全可仿真性。GUC框架中環境Z也可以訪問建模全局可信建立的理想功能M，這迫使仿真器S只能使用真正的M，也就不能從仿真M的過程中取得需要的陷門信息，因此GUC框架要求仿真器在與現實協議同樣的基礎上UC仿真成功，這使GUC安全的協議恢復了完全可仿真性。總結起來，GUC框架使用全局可信建立假定來保證通用可組合的安全計算的可實現性，同時使用 “仿真器只能使用與現實敵手同樣的 （真正的）全局可信建立”來保證完全可仿真性。

2.2 GUC框架可實現性研究

文獻 ［10］基于密鑰注冊模型KR［16］（使用FKR作為可信建立）提出了擴充的CRS模型ACRS（使用FACRS作為可信建立），并且提出了在ACRS模型中GUC仿真FCOM的一個協議UAIBC（文獻 ［14］展示了FCOM的可實現性蘊含通用可組合安全計算的可實現性）。下面給出了FACRS［10］。

Functionality FACRS

初始化階段：首次激活時，計算公共參考串PK←Setup（MSK），MSK是隨機選擇的 （比特的值。記錄對兒（PK，MSK）。

提供公鑰：當一個通信方索要該公共參考串，將PK返回給索要方和敵手。

休眠階段：當從一個腐敗通信方P收到一個消息 （retrieve，sid，P），將SK←Extract（PK，P，MSK）返回給P。如果這個消息是從誠實通信方收到的則忽略該消息。

協議UAIBC描述如下，其中承諾方為Pi，接收方為Pj，Pi要向Pj承諾一個比特b。方案中的Com是一個具有這個性質的承諾方案：知道接收方私鑰的承諾方可以給出模糊的承諾。EK是一個密集的OT－PRC安全的加密方案。

承諾階段：

（1）Pi向Pj發送 （commit，sid，Pi，Pj）；

（2）Pj生成隨機的k1←r｛0，1｝λ，計算 （ck，dk）＝Com（Pi，k1），并向Pi發送ck；

（3）Pi生成隨機的k2←r｛0，1｝λ，并將k2發送給Pj；

（4）Pj計算K＝k1／k2，并向Pi發送dk；

（5）Pi計算 （c，d）＝Com（Pj，b），并Pj向發送c和e。其中e的值是這樣確定的：如果b＝1，則e是一個隨機數；如果b＝0，則e＝EK’（r；d），K’＝k1’／k2，k1’＝Open（Pi；ck，dk）。

開啟階段：

（6）如果b＝0，則Pi向Pj發送b＝0，d，r；如果b＝1，則Pi向Pj發送b＝1，d。

（7）Pj驗證b＝Open（Pj；c，d）是否成立，如果b＝0還要驗證e＝EK（r；d）是否成立。

經仔細研究，UAIBC的原理是：

方案的隱藏性由E的安全性和Com的隱藏性擔保，當Pj不知道Pi的私鑰時成立。因為當Pj不知道Pi的私鑰時，Pj在計算 （ck，dk）＝Com（Pi，k1）時就不能給出模糊的k1，所以步驟 （2）～步驟 （4）的硬幣投擲協議所生成的密鑰K’＝K就是一個隨機的值，所以Pj無法從e求出d，也就無法求出b的值。

方案的綁定性由Com的綁定性擔保，當Pi不知道Pj的私鑰時成立。因為當Pi不知道Pj的私鑰時，Pi在計算 （c，d）＝Com（Pj，b）時就不能給出模糊的b。

方案的仿真可模糊性由Com的可模糊性和E的密文偽隨機性擔保，當Pj腐敗時成立。因為當Pj腐敗時，Pj從FACRS知道自己的私鑰，仿真器 （代替Pi運行程序）可以在此過程中知道Pj的私鑰，它就可以在計算 （c，d）＝Com（Pj，b）時給出模糊的b。

方案的仿真可提取性由E的可解密性擔保，當當Pi腐敗時成立。因為當Pi腐敗時，Pi從FACRS知道自己的私鑰，仿真器 （代替Pj運行程序）可以在此過程中知道Pi的私鑰，它就可以在計算 （ck，dk）＝Com（Pi，k1）時給出模糊的k1，進而可以在收到k2以后使K是那個它知道私鑰的K，當仿真器收到一個承諾c、e，它計算d＝D－1K（e），然后驗證 （c，d）＝Com（Pj，0）是否成立，若成立則b＝0，若不成立則b＝1，用這種方法就實現了仿真可提取性。

由以上研究可見，UAIBC使用全局可信建立FACRS的方式非常巧妙：

在現實協議中，若接收方腐敗了，則他想要破壞的是承諾的隱藏性，此時他需要知道承諾方的私鑰；若承諾方腐敗了，則他想要破壞的是承諾的綁定性，此時他需要知道接收方的私鑰；而理想功能FACRS只讓腐敗方知道自己的私鑰，而不能知道對方的私鑰，所以現實協議中的隱藏性和綁定性都不會被破壞，即現實協議具有隱藏性和綁定性，符合承諾的安全需求。

在理想協議中，若接收方腐敗了，則GUC框架需要擔保承諾的仿真可模糊性，此時仿真器需要知道接收方的私鑰；若承諾方腐敗了，則GUC框架需要擔保承諾的仿真可提取性，此時仿真器需要知道承諾方的私鑰；而理想功能FACRS正好讓腐敗方知道自己的私鑰，在此過程中仿真器可以知道腐敗方的私鑰，所以理想協議具有仿真可模糊性和仿真可提取性，符合GUC仿真的要求。

結合上面兩點，文獻 ［10］中的方案以完全可仿真的方式實現了通用可組合的承諾，進而可以以完全可仿真的方式實現安全計算。

2.3 GUC框架與UC框架及其改進版本的比較

由上節的研究可見，雖然GUC框架要求理想協議與現實協議使用同一個全局可信建立理想功能M，但是從可實現的GUC安全計算的情況來看，理想協議與現實協議對M的利用程度是不同的：FACRS使腐敗方知道自己的私鑰對現實協議是沒有幫助的，但是這點卻可以被理想協議大加利用，這實際上使仿真器比現實敵手擁有更強的能力。這使我們聯想到文獻 ［17］和文獻 ［18］中的框架，二者也是UC框架的改進版，下面我們比較這些框架。

文獻 ［17］中的框架允許仿真器擁有超多項式 （或者說準多項式）計算的能力，該能力通過調用超多項式時間的預言機來體現。文獻 ［17］證明了在其計算假定之下、在樸素模型中、針對非自適應主動敵手，任何良好形式的理想功能都可在該框架之下實現，當然也包括安全計算。

文獻 ［18］中的框架中現實敵手是均勻的PPT，而仿真器是非均勻的PPT。文獻 ［18］證明了在其計算假定之下、在沒有任何全局可信建立的情況下，在該框架中實現任何良好形式的理想功能都是可能的，當然也包括安全計算。

通過比較以上各框架我們得出，雖然各框架的建模技術多種多樣，但是能使包括安全計算在內的所有良好形式的理想功能以通用可組合的方式實現的框架都有一個共同的特點：仿真器的能力比現實敵手的能力強！表1給出了比較的結果，其中的可實現性是指對于任何良好形式的理想功能存在通用可組合的實現方案。

表1 GUC框架與UC框架及其改進版本的比較

3 結束語

本文分析了GUC框架解決的關鍵問題，研究了GUC框架解決問題的機理，還研究了實現GUC框架的方法，最后將GUC框架與UC框架及其改進版進行了比較。現存的所有通用可組合安全的承諾協議 （其存在性蘊含通用可組合安全計算的存在性）都以一種必要的方式使用了框架的這一特點：仿真器擁有比現實敵手更強的能力。是否任意良好形式的理想功能的可實現性蘊含仿真器擁有比現實敵手更強的能力是本文下一步研究的問題。

當前的全局可信建立FACRS是作為GUC框架的可行性證據而設計的。然而，為了使方案的常規安全性和通用可組合性同時成立，FACRS被故意設計為只讓腐敗通信方知道與其身份相關的私鑰。可是FACRS既然是由可信方執行的，那么，可信方讓腐敗的通信方比誠實的通信方知道更多的信息有悖常理；另一方面，腐敗的通信方向一個全局都信任的可信方告知自己腐敗的事實也有悖常理。研究能否找到GUC框架可行性的更現實、更有說服力的證據是本文未來的另一研究問題。

［1］RAN Canetti.Universal composable security：A new paradigm for cryptographic protocols ［C］.42nd Annual Symposium on Foundations of Computer Science.IEEE Computer Society，2001：136－145.

［2］Aggelos Kiayias，ZHOU Hongsheng.Trading static for adaptive security in universally composable zero－knowledge ［C］.34th International Colloquium，Automata，Languages and Programming，2007：316－327.

［3］Matthew Green，Susan Hohenberger.Universally composable adaptive oblivious transfer ［C］.International Crytology Conference，2008：179－197.

［4］SU Ting.Theory and application study on universally composable security［D］.Jinan：Shandong University，2009 （in Chinese）.［蘇婷.UC安全理論及應用研究 ［D］.濟南：山東大學，2009.］

［5］LEI Feiyu.Studies on UC secure multiparty computation and its applications［D］.Shanghai：Shanghai Jiaotong University，2007（in Chinese）.［雷飛宇.UC安全多方計算模型及其典型應用研究 ［D］.上海：上海交通大學，2007.］

［6］HONG Xuan.Studies on universally composable digital signature and its key problems［D］.Shanghai：Shanghai Jiaotong University，2008（in Chinese）. ［洪璇.通用可組合數字簽名模型及其關鍵問題研究 ［D］.上海：上海交通大學，2008.］

［7］GUO Yuanbo，WANG Chao，WANG Liangmin.Universally composable authentication and key exchange protocol for access control in spatial information networks ［J］.Acta Electronica Sinica，2010，38 （10）：2358－2364 （in Chinese）. ［郭淵博，王超，王良民.UC安全的空間網絡雙向認證與密鑰協商協議［J］.電子學報，2010，38 （10）：2358－2364.］

［8］LI Yahui，MA Jianfeng.Universally composable secure roaming authentication protocol for interworking networks ［J］.Computer Science，2010，37 （1）：47－50 （in Chinese）.［李亞暉，馬建峰.一種基于融合網絡通用可組合安全的漫游認證協議 ［J］.計算機科學，2010，37 （1）：47－50.］

［9］JIA Hongyong，QING Sihan， GU Lize，et al. Universally composable group key exchange protocol［J］.Journal of Electronics＆Information Technology，2009，31 （7）：1571－1575 （in Chinese）.［賈洪勇，卿斯漢，谷利澤，等.通用可組合的組密鑰交換協議 ［J］.電子與信息學報，2009，31 （7）：1571－1575.］

［10］RAN Canetti，Yevgeniy Dodis，Rafael Pass，et al.Universal composable security with global setup ［G］.LNCS 4392：Theory of Cryptography.Springer－Verlag，2007：61－85.

［11］Andrew C C Yao，Frances F Yao，ZHAO Yunlei.A note on the feasibility of generalized universal composability ［C］.Proceedings of The 4th International Conference on Theory and Applications of Models of Computation，2007：474－485.

［12］RAN Canetti，Eyal Kushilevitz，Yehuda Lindell.On the limitations of universally composable two－party computation without set－up assumptions ［G］.LNCS 2656：Advances in Cryptology，2003：68－86.

［13］RAN Canetti，Yehuda Lindell，Rafail Ostrovsky，et al.Uni－versally composable two－party and multi－party computation［C］.Proceedings of The Thiry－Fourth Annual ACM Symposium on Theory of Computing，2002：494－503.

［14］Jonathan Katz.Universally composable multi－party computation using tamper－proof hardware ［C］.Proceedings of the 26th Annual International Conference on Advances in Cryptology，2007：115－128.

［15］Rafael Pass.On Deniabililty in the common reference string and random oracle models ［C］.Proceedings of CRYPTO，2003：316－337.

［16］BOAZ Barak，RAN Canetti，Jesper Buus Nielsen，et al.Universally composable protocols with relaxed set－up assumptions［C］.Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science，2004：186－195.

［17］Manoj Prabhakaran，Amit Sahai.New notions of security：Achieving universal Composability without trusted setup ［C］.Proceedings of The Thirtysixth Annual，2004：242－251.

［18］LIN Huijia，Rafael Pass，Muthuramakrishnan Venkitasubramaniam.A unified framework for concurrent security：Universal composability from stand－alone non－malleability ［C］.Proceedings of the 41st Annual ACM Symposium on Theory of Computing，2009：179－188.