基于歷史頻繁模式的交通流預測算法

鐘慧玲，鄺朝劍，黃曉宇，蔡文學

（1.華南理工大學 經濟與貿易學院，廣東 廣州510006；2.中國移動，廣東 東莞523129）

0 引 言

交通流預測是利用交通流信息選擇最合適的模型和方法來預測未來一段時間的交通狀況，預測結果可廣泛應用于交通誘導、出行路線規劃等領域。根據預測時段的長短，分為短時交通流預測 （15分鐘內）和中長期預測［1］。

目前，常用的預測模型有時間序列模型［2］、卡爾曼濾波模型［3］、非參數回歸模型［4］、神經網絡模型［5］、支持向量機［6］以及這些模型的組合模型［7－8］。隨著研究的深入，有學者將數據挖掘方法引入交通流預測［9－10］。文獻［10］提出了基于K近鄰的非參數回歸方法，通過挖掘歷史數據中的K最近鄰，擬合成預測值，然而該方法需要維護龐大且有代表性的歷史數據庫。文獻［11］通過研究發現道路交通流具有自身的規律，通過挖掘這些規律，可對道路的交通流進行預測。總結國內外研究，主要存在以下兩個問題：一是通過增加模型的復雜性來提高預測精度，計算量大，不能很好滿足實時要求；二是研究集中于短時交通流預測，支持中長期交通流預測的模型較少。

針對這兩個問題，在張濤和戢曉峰的研究基礎上，本文提出基于歷史頻繁模式的交通流預測算法，通過挖掘道路交通流的歷史頻繁模式，結合道路實時的交通信息，進行交通流預測。與基于K近鄰的非參數回歸方法不同，本文提出算法使用歷史數據中頻繁出現的交通流模式進行預測，而不是簡單使用歷史數據擬合成預測值，更強調交通流出現的規律性；而且，預測模型更簡單。經實例證明，算法具有較高預測精度、且支持交通流短時和中長期預測。

1 基于歷史頻繁模式的交通流預測算法

1.1 算法框架

基于歷史頻繁模式的交通流預測算法是一種數據驅動的預測方法，通過挖掘交通流歷史數據的頻繁模式，與當前獲取的實時交通信息進行模式匹配，預測未來一段時間內道路的交通狀況。算法的關鍵因素是交通流歷史頻繁模式的挖掘和預測算法的構建，其流程如圖1所示。

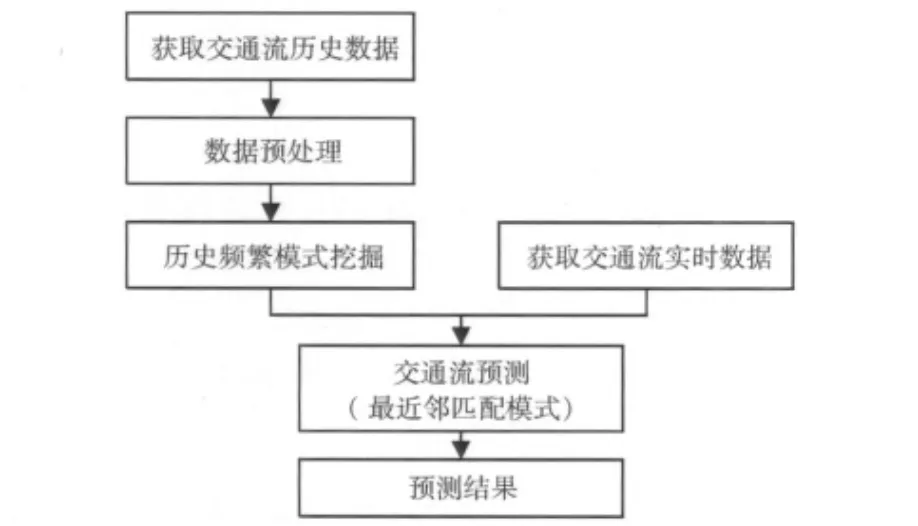
圖1 基于歷史頻繁模式的交通流預測算法流程

1.2 交通流歷史頻繁模式挖掘

頻繁模式挖掘是數據挖掘領域一個重要的研究內容，廣泛應用于商業分析、Web數據挖掘和生物序列分析，然而，在交通流預測中還沒有相關應用。目前，國內外學者提出了許多挖掘頻繁模式的算法，如Apriori算法、GSP算法、SPADE算法、FreeSpan算法等［12－14］，然而，這些算法在挖掘頻繁模式時，大多采用精確匹配，要求相同的模式在數據庫中重復出現，且算法效率低，挖掘的模式有冗余。在實際應用中，絕對相同的模式很少，因此，挖掘近似的頻繁模式更有意義。H.C.Kum等［15］提出了挖掘數據庫中近似頻繁模式的ApproxMAP算法，該算法有效且高效，能挖掘出長頻繁模式。這里，結合ApproxMAP算法挖掘交通流歷史頻繁模式。

1.2.1 相關定義

設I＝ ｛i1，i2，…，in｝是由n個不同的項組成的集合，I的子集稱為項集。序列就是由若干個項集組成的有序列表，一個交通流時間序列S表示為＜s1，s2，…，sn＞，其中si為項集 （即交通狀況），可表示為 （x1，x2，…，xn），當si只包含一項時，可省略括號。長度為L的序列記為L－序列。

定義1 對于交通流時間序列數據庫中的序列X，X的支持度定義為序列X在數據庫中出現的次數，記為support（X）。

定義2 給定最小支持度閾值min＿sup，如果序列X的支持度support（X）≥min＿sup，則稱序列X為頻繁序列。

定義3 給定最小距離閾值min＿dist，序列X的近似支持度定義為數據庫中與X的編輯距離不超過min＿dist的另一序列Y的數目；如果序列X的近似支持度不小于給定的min＿sup，則稱序列X為近似頻繁序列。

1.2.2 挖掘算法

結合ApproxMAP算法的交通流歷史頻繁模式挖掘算法主要包含兩個階段。一是交通流歷史數據分類，通過聚類算法，把相關性較強的交通流歷史數據分成一類；二是在交通流歷史數據分類的基礎上，對每一分類的數據進行多序列比對，挖掘出交通流歷史頻繁模式。

為了對交通流歷史數據進行有效分類，原始數據經噪聲數據處理和缺失數據填充預處理之后，以5分鐘劃分間隔，使用符號累積近似 （SAX）技術［16］按5級把交通流歷史數據轉化成交通流歷史數據時間序列，計算序列間交通流的相似性。這里，使用編輯距離來度量兩交通流序列之間的相似性，編輯距離越小，相似性越大。給定序列X＝＜x1，x2，…，xn＞和Y＝＜y1，y2，…，ym＞的編輯距離可用以下動態規劃算法求解。

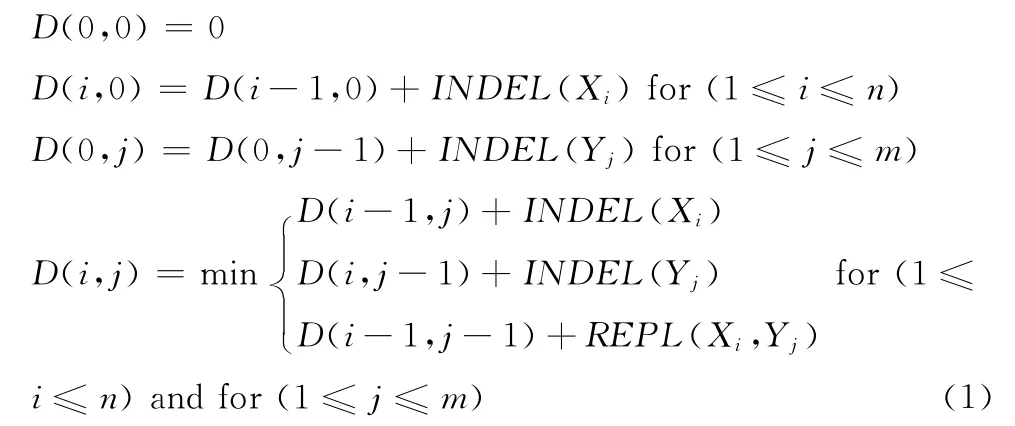
然后，使用基于密度的K最近鄰聚類算法將這些交通流歷史數據時間序列根據交通流的相似程度劃分到不同的類中，其主要步驟如下。

（1）初始化每一交通流序列為一類。對每一類中的序列Si，令Density（CSi）＝Density（Si）；

（2）基于序列密度合并近鄰。對于每一個交通流序列Si，設Si1，…，Sin為其編輯距離不大于dk的近鄰；對于每一個交通流序列Si∈ ｛Si1，…，Sin｝，如果Density（Si）＜Density（Sj）且 不 存 在S′j滿 足：dist（Si，S′j） ＜dist（Si，Sj）且Density（Si）＜Density（S′j），合并Si和Sj所在類CSi和CSj，令新類密度為：max ｛Density（CSi），Density（CSj）｝；

（3）基于類密度合并。對交通流時間序列中所有序列Si，如果不存在序列密度大于其的近鄰，但存在一些密度等于Density（Si）的近鄰Sj，如果Density（CSi）＞Density（CSj），合并Si和Sj所在類CSi和CSj。

其中，交通流序列Si的密度為

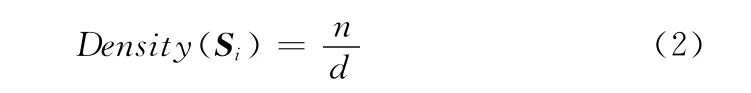
式中，d＝max｛d1，d2，…，dk｝——交通流序列Si與其他序列的編輯距離的第k最小值，k——用戶定義參數，n＝ ｛Sj∈S｜dist（Si，Sj）≤d｝ ——所有交通流序列中與序列Si的編輯距離不大于d的序列的數目。

對交通流歷史數據進行分類后，可使用多序列比對方法，挖掘每一分類的交通流歷史數據的近似頻繁模式。定義 “交通狀況加權序列”結構為 “WS＝＜X1：v1，…，Xl：vl＞：n”，一個交通狀況加權序列包含以下信息：

（1）當前類中包含n個交通流序列，且n是交通狀況加權序列的全局權重；

（2）當前類中，有vi個交通流序列在位置i包含交通狀況項目集Xi（1≤i≤l）；

（3）交通狀況加權序列中每個交通狀況項目集格式為Xi＝ （xj1：wj1，…，xjm：wjm），表示在當前類中，有wjk個交通流序列在位置i包含xjk（1≤i≤l且1≤k≤m）。

對于交通狀況加權序 列WS＝＜ （x11：w11，…，x1m1：w1m1）：v1，…，（xl1：wl1，…，xlm1：wlm1）：vl＞：n，位置i的交通狀況項目集xij：wij的支持度定義為

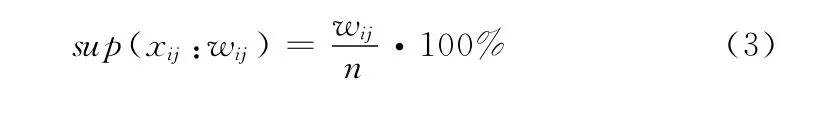
交通狀況項目集的支持度越大表示該交通狀況在交通流歷史數據中被更多的序列包含。通過定義最小支持度閾值min＿sup（0≤min＿sup≤1），從交通狀況加權序列中移除支持度小于min＿sup的項目，得到滿足支持度要求的近似頻繁模式。

假設聚類后交通流序列S1＝＜1，1，2，2，3＞、S2＝＜1，2，1，3，2＞和S3＝＜2，1，3，2，2＞合成一類，其交通狀況加權序列計算如表1所示。定義最小支持度閾值min＿sup＝0.5，則類中近似頻繁模式為＜1，1＞和＜2，2＞。

表1 加權序列計算

1.3 預測算法

結合ApproxMAP算法可以有效地挖掘出交通流歷史頻繁模式，在此基礎上，通過結合獲取的實時交通信息，可對交通狀況進行預測。利用滑動窗口技術，通過逐項計算實時交通信息序列與等長的歷史頻繁子模式的相似性，根據最近鄰匹配原則，選擇交通流相似度最大時的最佳點進行預測。交通流預測算法流程如圖2所示。

2 實驗與分析

交通流預測要求預測結果有效、準確，以保證交通誘導、出行路線規劃等應用的可行性。為了驗證本文提出的基于歷史頻繁模式的交通流預測算法的有效性和準確性，使用從珠海市城市路網中采集的真實的GPS浮動車數據，隨機選取實驗路段和預測時間，對提出的算法進行重復實驗，統計預測值與實際值的平均誤差。

2.1 數據來源

實驗數據來自于珠海市城市路網采集的GPS浮動車數據，如表2所示。隨機選取路網中的10條路段作為實驗樣本，使用的實驗數據見 “歷史數據”和 “測試數據”所示。其中，“歷史數據”是用于挖掘交通流歷史頻繁模式的數據，“測試數據”為用于預測與對比的隨機選取的某天數據。

2.2 結果分析

實驗對不同的預測時長，隨機選取100個時段進行交通流預測，以全面考慮在不同交通狀況 （高峰、閑時）下算法的有效性和準確性，以及算法的穩定性。實驗內容包括算法準確性分析、參數影響、以及與基于K近鄰的非參數回歸預測算法的對比。

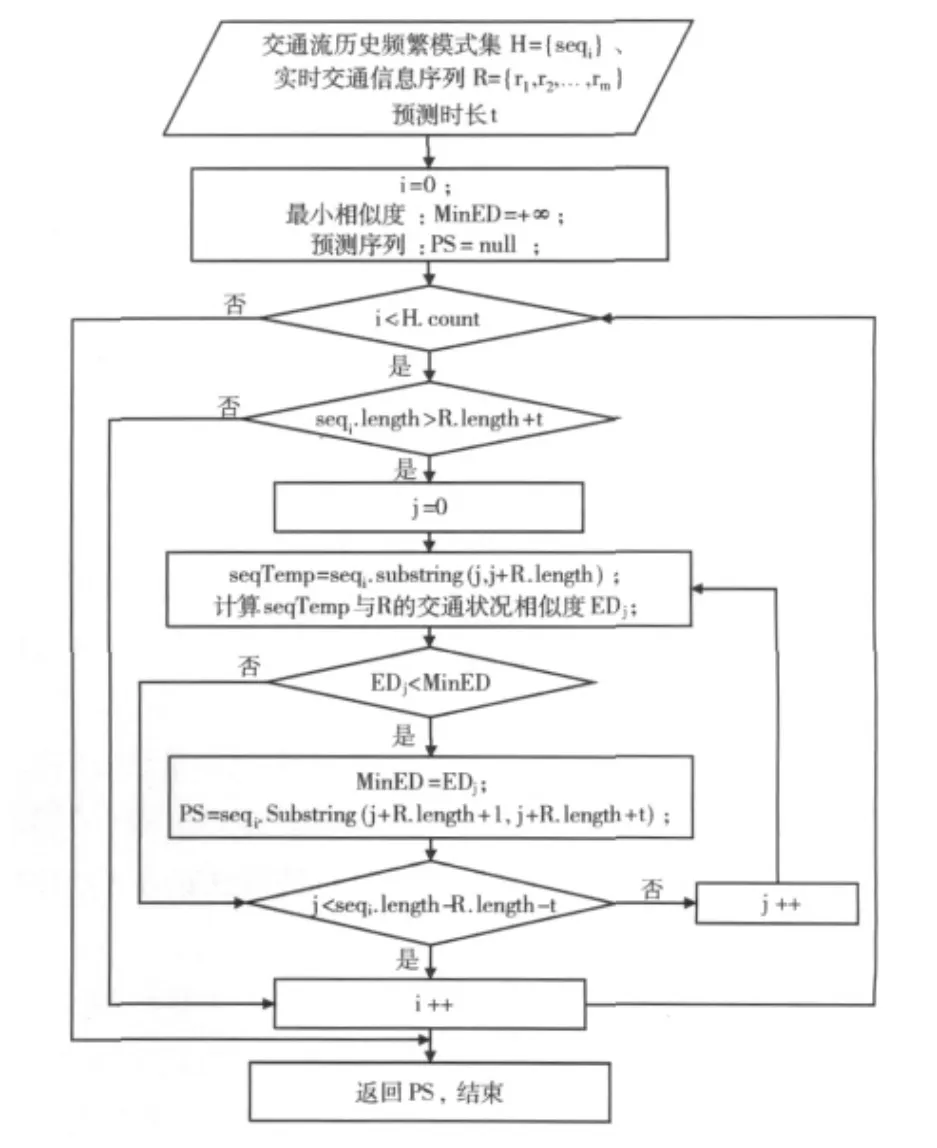
圖2 預測算法流程

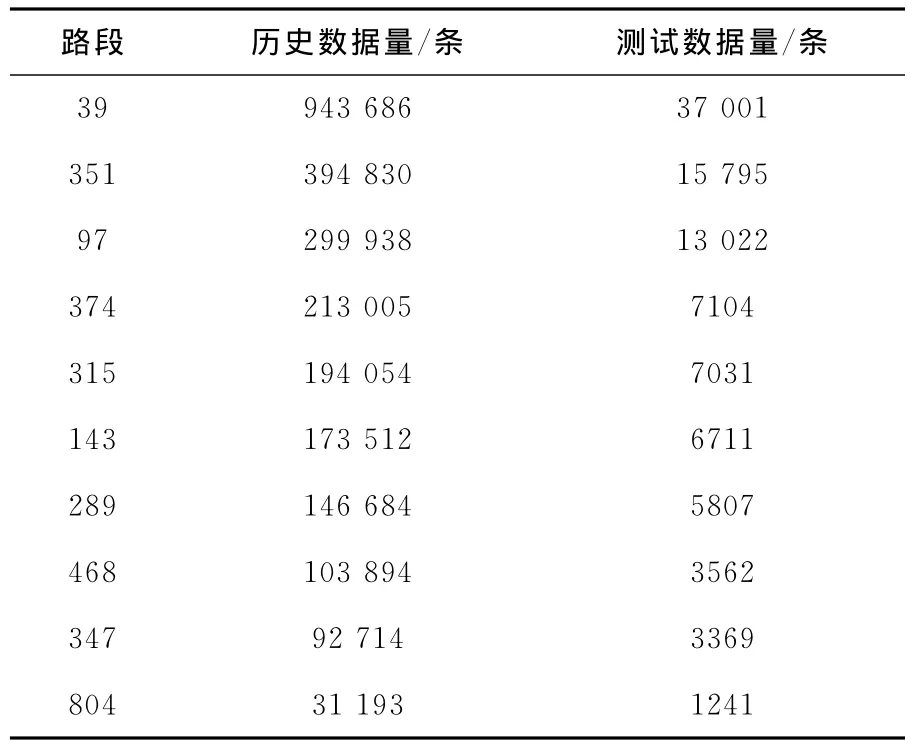
表2 實驗數據量

2.2.1 算法準確性分析

為了驗證算法的有效性和準確性，實驗選取近鄰參數K＝5，最小支持度參數min＿sup＝0.5，分別設置預測時長為15分鐘、30分鐘、45分鐘和60分鐘，對于每個預測時長，隨機選取起止時間預測100次，計算真實值與預測值標準差的均值。實驗結果如圖3所示。

圖3 交通流預測誤差結果

結合實際路網拓撲和圖3結果，發現算法對交通狀況平穩的道路預測精度較高，而對交叉路口 （特別是存在信號燈路口）上的道路，由于其交通狀況波動較大，預測精度稍差。

從圖3還知，算法對隨機選取的10條道路的平均誤差約為0.35。為了驗證算法的平均預測誤差不超過0.3，我們進行t檢驗 （假設H0：μ≤0.3，H1：μ＞0.3），設置顯著性水平α＝0.05，分別對各個預測時長的統計量進行右邊檢驗，得到的P值分別為0.495、0.495、0.444和0.393，均大于α＝0.05，因此，接受假設H0，即算法的平均預測誤差不超過0.3。

此外，為了說明算法對中長期交通流預測和短時交通流預測 （15分鐘內）具有同樣的預測精度，我們對預測時長為15分鐘與30分鐘、15分鐘與45分鐘、15分鐘與60分鐘的實驗結果進行了配對t檢驗，設置顯著性水平α＝0.05，得到雙尾檢驗的P值分別為1.00、0.718和0.537，均大于α＝0.05，因此，算法對交通流進行中長期預測具有與短時預測同樣高的預測精度。

2.2.2 參數影響

算法具有兩個關鍵參數，最近鄰參數K和最小支持度參數min＿sup，H.C.Kum已經通過實驗確定最佳參數K的選取范圍為 ［3，10］，可根據歷史數據的規模進行設置。因此，這里主要討論最小支持度參數min＿sup對算法的影響。

通過固定參數K取值，選取不同的min＿sup值進行實驗來分析參數min＿sup對算法的影響。實驗設置近鄰K取值范圍為 ［4，7］，對于每一個預測時長和每條隨機選取實驗路段，隨機選取起止時間預測100次，計算預測值與真實值的標準差，然后統計所有道路預測誤差的均值。實驗結果如圖4所示。

由圖4可知，固定參數K時，參數min＿sup在 ［0.3，0.7］范圍內取值對預測結果的精度影響不大。然而，如果最小支持度參數min＿sup設置過大，會減少挖掘到的交通流歷史頻繁模式的數量，因此，在實際應用中，為了保證挖掘到更多的交通流歷史頻繁模式用于預測，建議min＿sup取值范圍為 ［0.3，0.5］。

2.2.3 算法對比

使用本文提出的算法與張濤等提出的基于K近鄰的非參數回歸方法進行實驗對比，本文算法選取參數K＝5，min＿sup＝0.5，基于K近鄰的非參數回歸方法近鄰K取值范圍為 ［1，20］。對于每一個預測時長，和每條隨機選取實驗路段，隨機選取起止時間預測100次，計算預測值與真實值的標準差，然后統計所有道路預測誤差的均值，實驗結果如圖5所示。

計算不同預測時長 （5－60分鐘）下各算法預測誤差均值的方差，本文算法的方差為0.0003，而基于K近鄰的非參數回歸方法當K＝20時方差最小，為0.0048，遠大于本文算法。結合圖5中實驗結果可以發現，本文提出算法的預測性能比基于K近鄰的非參數回歸方法穩定，且中長期預測與短時預測具有同樣高的精度，預測誤差波動不大，而基于K近鄰的非參數回歸方法預測誤差波動較大，預測性能不穩定。

3 結束語

通過深度挖掘交通流歷史數據的規律，本文提出的基于歷史頻繁模式的交通流預測算法能有效地對交通流進行短時和中長期預測，且具有中長期預測與短時預測具有同樣高的預測精度、受參數影響小的優點。最后，與基于K近鄰的非參數回歸預測方法進行對比，結果表明基于歷史頻繁模式的預測方法具有更高的預測精度和預測性能，預測誤差波動更小。通過實驗還發現，算法要求有足夠的數據量支持以有效地挖掘出用于預測的交通流歷史頻繁模式，道路數據量越豐富，預測精度越高，因此，可以將浮動車數據與環形感應線圈數據進行融合，提高數據的數量和質量，進而提高算法的適用性。此外，還可以進一步考慮路網中道路間的空間相關性，從時空角度挖掘交通流規律，增加預測結果的準確性。

圖4 參數min＿sup取不同值時實驗結果

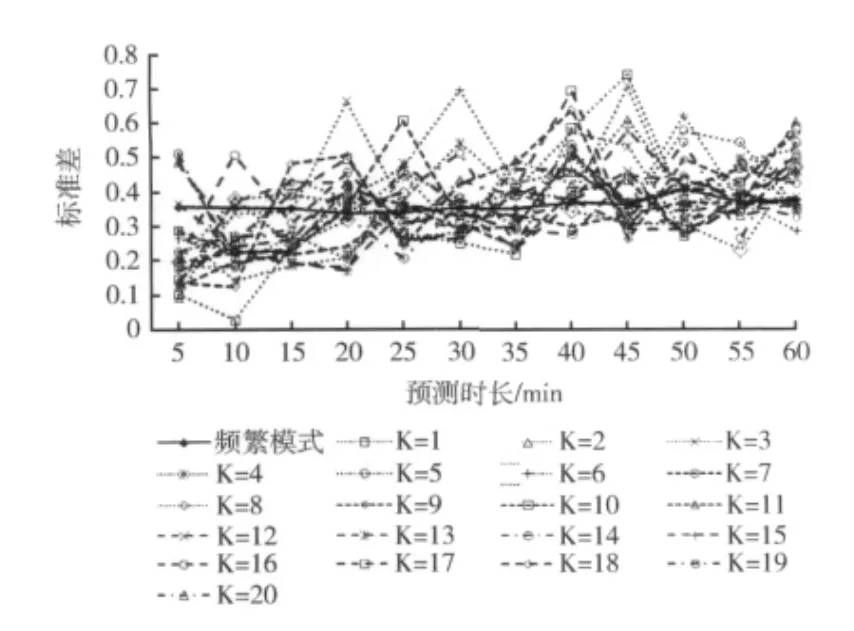
圖5 與基于K近鄰的非參數回歸方法對比結果

［1］LU Haiting，ZHANG Ning，HUANG Wei，et al.Research progress of short term traffic flow prediction methods ［J］.Journal of Transportation Engineering and Information，2009，7 （4）：84－91 （in Chinese）.［陸海亭，張寧，黃衛，等.短時交通流預測方法研究進展 ［J］.交通運輸工程與信息學報，2009，7 （4）：84－91.］

［2］DONG H H，JIA L M，SUN X L，et al.Road traffic flow prediction with a time－oriented ARIMA model ［C］.International Joint Conference on INC IMS and IDC，2009.

［3］Abdi J，Moshiri B，Jafari E，et al.Traffic state variables estimating and predicting with extended Kalman filtering ［C］.International Conference on Power Control and Embedded Systems，2010.

［4］ZHANG T，HU L F，LIU Z X，et al.Nonparametric regression for the short－term traffic flow forecasting ［C］.International Conference on Mechanic Automation and Control Engineering，2010.

［5］Gültekin Cetiner B，Murat Sari，Oˇguz Borat.A neural network based traffic－flow prediction model［J］.Mathematical and Computational Applications，2010，15 （2）：269－278.

［6］SUN D Z，WANG Q X，JIANG X Q.The application of support vector machines （SVM）for traffic condition prediction using ITS data ［C］.Proceedings of the Conference on Traffic and Transportation Studies，2010.

［7］GUO X，DENG F Q.Short－term of intelligent traffic flow based on BP neural network and ARIMA model［C］.International Conference on E－Product E－Service and E－Entertainment，2010.

［8］YE Yan，LU Zhilin.Neural network short－term traffic flow forecasting model based on particle swarm optimization ［J］.Computer Engineering and Design，2009，30 （18）：4296－4298（in Chinese）.［葉嫣，呂智林.基于粒子群優化的神經網絡短時交通流量預測 ［J］.計算機工程與設計，2009，30 （18）：4296－4298.］

［9］YAN Wei，LIU Yungang，WANG Guihua，et al.Data mining using in a novel traffic flow forecasting model［J］.Systems Engineering－Theory ＆ Practice，2010，30 （7）：1320－1325 （in Chinese）.［閆偉，劉云崗，王桂華，等.基于數據挖掘的交通流預測 模 型 ［J］. 系 統 工 程 理 論 與 實 踐，2010，30 （7）：1320－1325.］

［10］ZHANG Tao，CHEN Xian，XIE Meiping，et al.K－NN based nonparametric regression method for short－term trafficflow forecasting ［J］.Systems Engineering－Theory ＆ Practice，2010，30 （2）：376－384 （in Chinese）.［張濤，陳先，謝美萍，等.基于K近鄰非參數回歸的短時交通流預測方法［J］.系統工程理論與實踐，2010，30 （2）：376－384.］

［11］JI Xiaofeng.An overview on methods of urban road traffic state analysis and their prospect ［J］.Road Traffic ＆Safety，2008，9 （6）：11－15 （in Chinese）.［戢曉峰.城市道路交通狀態分析方法回顧與展望 ［J］.道路交通與安全，2008，9（6）：11－15.］

［12］Aaron Ceglar，John F Roddick.Association mining ［J］.ACM Computing Surveys， 2006， 38 （2 ）： DOI 10. 1145／1132956.1132958.

［13］HAN J，CHENG H，XIN D，et al.Frequent pattern mining：Current status and future directions ［J］.Data Min Knowl Disc，2007，15 （1）：55－86.

［14］PEI Jian，HAN Jiawei，WANG Wei.Constraint－based sequential pattern mining：The pattern－growth methods ［J］.Journal of Intelligent Information Systems，2007，28 （2）：133－160.

［15］KUM H C，CHANG J H，WANG W.Benchmarking the effectiveness of sequential pattern mining methods ［J］.Data and Knowledge Engineering，2007，60 （1）：30－50.

［16］Jessica Lin，Eamonn Keogh，LI Wei，et al.Experiencing SAX：A novel symbolic representation of time series ［J］.Data Mining and Knowledge Discovery，2007，15 （2）：107－144.