基于增量Kalman濾波的GPS多路徑效應系統誤差研究

伍錫銹

（廣州市城市規劃勘測設計研究院，廣東 廣州 510060）

GPS高精度定位應用中，多路徑效應誤差是一個最主要的誤差來源，近年來很多對GPS接收機信號處理的方法，如窄相關技術、多路徑消減技術等都可有效地消減多路徑效應的影響，但是其殘余多路徑效應誤差對高精度GPS應用仍具有很大的影響，且由于其本身的復雜性，所以該研究一直以來均是GPS數據處理研究的熱點。多路徑效應誤差其主要表現為系統性誤差，但是其特性復雜，既具有延續性，又具有偶然性，因而很難用統一的確定的模型來準確描述它。目前，對于該類系統誤差通常采用的方法是將其視為平差模型的模型誤差，利用函數模型或隨機模型或二者之間綜合作用來予以補償，從整體上減弱或消除其影響，以保證平差結果的高精度。具體有以下幾種：附加系統參數的參數平差法、附加系統權法、附加系統參數和系統法、選群擬合法和半參數法［1－4］。

Kalman濾波方法是一種從帶有噪聲干擾的信號中提取有用信號的參數最優估計方法，目前廣泛應用于信號處理和導航定位等領域，并經過諸多學者的研究和改進發展了一系列的濾波方法，包括擴展Kalman濾波、抗差自適應Kalman濾波、粒子濾波等等［5－8］。但是，Kalman濾波最優估計是建立在動態噪聲和觀測噪聲均為白噪聲的假設條件下推得的一種遞推濾波方法，即觀測不含系統性誤差影響。在GPS高精度定位應用中，由于多路徑效應系統誤差的干擾，將會很大程度上影響Kalman濾波估計值的精度和可靠性，乃至使濾波結果發散，但是實際應用中相鄰2個觀測向量的系統誤差大小比較接近，即認為在較短的觀測時間段內，觀測系統誤差有微小的變化，那么相鄰觀測向量之差即觀測向量增量中所含的系統誤差較小，其能夠滿足Kalman濾波觀測噪聲為白噪聲的假設條件。從而在本文中對利用觀測向量的增量Kalman濾波極其在GPS多路徑效應系統誤差的應用進行研究。

1 增量Kalman濾波

在標準Kalman濾波中設系統狀態方程和觀測方程分別為

式中：Xk為狀態向量，Φk，k－1為狀態轉移矩陣，Lk為觀測值向量，Ak為設計矩陣，Wk和ek均是均值為0且協方差矩陣分別為∑Wk和∑k的正態白噪聲。假設ΔLk＝Lk－Lk－1為觀測向量增量，則增量Kalman濾波的增量觀測方程可以表示為

其中：vk＝ek－ek－1，由于諸多實際中相鄰觀測向量Lk和Lk－1的測量系統誤差大小比較接近，所以ΔLk的系統誤差相對較小，并假設其服從均值為0協方差矩陣為Rk的正態白噪聲。

增量Kalman濾波的狀態向量Xk的最佳估值可以由下面一組遞推公式實現：

1）計算預測狀態向量：

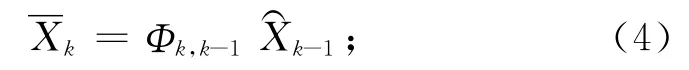
2）計算預測狀態協方差矩陣：

3）計算信息向量：

4）計算增益矩陣：

5）計算新的狀態估值：

6）計算新的狀態向量協方差矩陣：

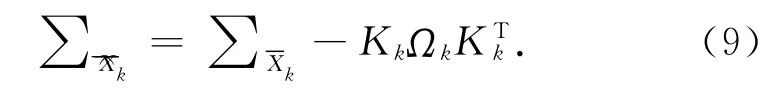
經過該遞推公式實現的增量Kalman濾波估計，其得到的狀態估計具有無偏性，即E（）＝E（Xk），具體可參考文獻［9］。

2 實例計算分析

試驗地點選在香港理工大學的教學樓上，基準站使用Topcon雙頻接收機，天線類型為Topcon CR3扼流圈天線，流動站為Septentrio接收機和普通測地型天線，基線長度約3.997m，數據采樣頻率為1Hz，測站周圍有較多的玻璃幕墻高樓，多路徑效應影響比較嚴重。數據預處理過程如下：首先通過對較長時間的靜態觀測解算得到基線向量信息；然后利用該基線先驗信息逐歷元解算出測點的動態軌跡，從而得到局部坐標系下相對于該基線信息的三維坐標殘差序列，解算軟件為GPSSM軟件［10］。由于基線距離非常短，在雙差觀測方程中，衛星鐘差和接收機鐘差能夠比較好地得到消除，電離層、對流層、衛星軌道誤差影響可以被忽略，其主要誤差來源為多路徑效應和接收機的高頻噪聲。下面從中提取X方向100min的觀測數據進行處理，為對比分析本文方法處理效果，現采用2種方案分別進行處理。方案1：標準Kalman濾波方法，處理效果如圖1所示；方案2：增量Kalman濾波處理方法，處理效果如圖2所示。分別繪出濾波處理前后的觀測殘差序列圖、觀測向量增量坐標序列圖（見圖3）和誤差統計結果見表1，圖1中RAW表示為濾波處理前的坐標序列數據，SKF、IKF分別表示為經過標準Kalman濾波和增量Kalman濾波處理之后的坐標序列。

表1 誤差統計結果 mm

圖3 觀測向量增量坐標序列

從計算結果可以看出：

1）觀測殘差中不僅含有較強的偶然噪聲，而且還含有比較嚴重的多路徑低頻系統性誤差。

標準Kalman濾波對于觀測誤差中的偶然噪聲具有較好的去噪作用，但是對于其中的系統誤差的作用效果較小。

2）從圖2和誤差統計結果可以看出增量Kalman濾波能夠比較有效地消除多路徑效應系統誤差的影響，從而提高濾波精度，證明本方法具有一定的可行性和有效性。

3）圖3中可以看出，相鄰2個量測向量的測量觀測系統誤差大小比較接近，其增量向量所含的系統誤差相對很小，并且其更能夠滿足Kalman濾波所假設的觀測向量服從相互獨立、期望為零的高斯分布條件。

3 結束語

在實際應用中尤其是對于短基線，在雙差觀測方程中，衛星鐘差和接收機鐘差能夠比較好的得到消除，電離層、對流層、衛星軌道誤差影響可以被忽略，其主要誤差來源為多路徑效應和接收機的高頻噪聲，而相鄰觀測歷元多路徑誤差相差較小，從而利用增量Kalman以提高濾波估計的精度和可靠性，以及本文方法對于該類型的系統誤差具有較好的處理效果，并且計算簡單，便于工程應用。

［1］李萬年，王振杰.基于半參數模型的高精度GPS基線處理中系統誤差的分離［J］.山東理工大學學報：自然科學版，2005，19（6）：18－24.

［2］王振杰，盧秀山.利用半參數模型分離GPS基線中的系統誤差［J］.武漢大學學報：信息科學版，2007，32（4）：316－318.

［3］歐吉坤，王振杰.精密測量中系統誤差的分離方法［J］.數據采集與處理，2003，18（4）：365－368.

［4］周江文.系統誤差的數學處理［J］.測繪工程，1999，8（2）：1－4.

［5］楊元喜，張雙成.導航解算中的系統誤差及其協方差矩陣擬合［J］.測繪學報，2004，33（3）：189－194.

［6］楊元喜.自適應動態導航定位［M］.北京：測繪出版社，2006.

［7］Yang Y，He H，Xu G.Adaptively robust filtering for Kinematic geodetic positioning［J］.Journal of Geodesy，2001，75（2）：109－116.

［8］Yang Yuanxi，Xu Tianhe.An Adaptive Kalman Filter Based on Sage Windowing Weights and Variance Components［J］.The Journal of Navigation，2003，56（2）：231－240.

［9］傅惠民，吳云章，婁泰山.欠觀測條件的增量Kalman濾波方法［J］.機械強度，2012，34（1）：43－47.

［10］戴吾蛟.GPS精密動態變形監測的數據處理方法研究［D］.長沙：中南大學，2007.