衛(wèi)星重力梯度恢復地球重力場的頻譜分析

蔡 林，周澤兵，祝 竺，高 防，許厚澤

1 華中科技大學電子與信息工程系，武漢 430074

2 華中科技大學物理學院，武漢 430074

3 華中科技大學地球物理研究所，武漢 430074

4 中國科學院測量與地球物理研究所，武漢 430077

衛(wèi)星重力梯度恢復地球重力場的頻譜分析

蔡 林1，3，周澤兵2，3＊，祝 竺2，3，高 防2，3，許厚澤3，4

1 華中科技大學電子與信息工程系，武漢 430074

2 華中科技大學物理學院，武漢 430074

3 華中科技大學地球物理研究所，武漢 430074

4 中國科學院測量與地球物理研究所，武漢 430077

根據(jù)儀器功率譜密度和重力位系數(shù)階方差的定義，本文建立了衛(wèi)星重力梯度測量噪聲功率譜密度與重力場模型的誤差階方差的直接對應關(guān)系，并基于此討論了重力梯度測量精度、衛(wèi)星軌道高度以及運行時間對地球重力場恢復精度的影響.相比于傳統(tǒng)的基于最小二乘法評估衛(wèi)星載荷噪聲對地球重力場恢復精度的影響而言，本文提出的方法簡單、直接，有助于快速設計和確定衛(wèi)星重力測量計劃的有關(guān)參數(shù).

衛(wèi)星重力梯度測量，地球重力場，頻譜分析

1 引 言

衛(wèi)星重力測量技術(shù)公認為是當今獲取全球高精度高分辨率地球重力場及其時變信息最有效的技術(shù)手段之一.于2000年7月15日和2002年3月17日分別發(fā)射升空的CHAMP衛(wèi)星［1］和GRACE衛(wèi)星［2］采用的是衛(wèi)衛(wèi)跟蹤（SST）觀測技術(shù)，測量了地球重力場的中長波分量.2009年3月17日成功發(fā)射的GOCE衛(wèi)星［3－4］結(jié)合了高低衛(wèi)－衛(wèi)跟蹤模式和衛(wèi)星重力梯度測量（SGG）兩種技術(shù)模式.相對于CHAMP和GRACE而言，GOCE能更為精確地測量地球重力場的中短波分量，對地球的位系數(shù)測量能達到200階以上.

地球重力場的恢復精度取決于衛(wèi)星的測量模式、衛(wèi)星高度、軌道傾角、衛(wèi)星載荷的測量精度等參數(shù).目前在衛(wèi)衛(wèi)跟蹤（SST）測量的數(shù)據(jù)處理和誤差分析中廣泛采用的是利用基于軌道攝動分析理論的時域法，包括動力學積分法［5－6］、能量守恒法［7－8］和短弧邊值法［9］等.對于衛(wèi)星重力梯度數(shù)據(jù)的處理和評估，一般是基于將重力梯度觀測值作為衛(wèi)星位置或者時間的函數(shù)，在此基礎上利用相應的空域最小二乘法［10－11］或時域最小二乘法［10，12－13］來確定重力場模型并進行誤差分析.以上這些方法本質(zhì)上都是利用最小二乘法評估重力場恢復精度［14－15］，能夠在得到重力位系數(shù)的同時給出相應重力場恢復的精度，以及可以把不同測量數(shù)據(jù)組合進行聯(lián)合求解，得到優(yōu)化的結(jié)果.這類方法不僅需要消耗大量計算資源，且難以直接評估某些單一參數(shù)的影響.另外，當前和未來的重力場研究都面臨著解算模型的分辨率越來越高、階數(shù)越來越大的問題.如果使用傳統(tǒng)方法研究誤差分析和恢復能力，則在階數(shù)較大時，每增加一階都會使計算量急劇增長并帶來嚴重的數(shù)值不穩(wěn)定性問題［16］.所以，高效、穩(wěn)定的評估重力場精度的方法對高分辨率重力場模型的研究有著重要意義.

為了快速評估和確定衛(wèi)星重力測量計劃有關(guān)參數(shù)，以及評估不同類型載荷噪聲功率譜的影響，本文根據(jù)儀器功率譜密度和重力位模型階方差的定義，討論了重力梯度測量噪聲與地球重力場的頻譜關(guān)系，建立起地球重力場恢復精度與儀器噪聲水平的直接表達式，這有助于項目設計初期選取和確定相應載荷指標，以及分析部分載荷指標調(diào)整的影響.最后，本文利用該方法對衛(wèi)星重力梯度測量中儀器技術(shù)指標、衛(wèi)星高度和運行時間與恢復地球重力場的精度之間的關(guān)系作了模擬分析.

2 理論分析

地球引力場擾動位函數(shù)T的球諧展開如下［10］：

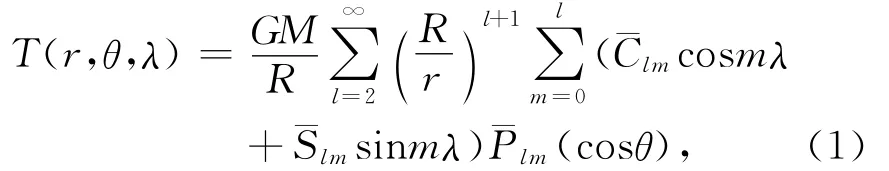
其中GM為地心引力常數(shù)，R為地球平均半徑，l和m分別為球諧展開的階和次，與為相對于正常重力位的擾動球諧系數(shù)，（cosθ）為歸一化的勒讓德函數(shù)，r、θ和λ分別為地心參考系下觀測點的半徑、余緯和經(jīng)度，r＝R＋H，H表示衛(wèi)星軌道高度.

對（1）式求導并利用相關(guān)坐標關(guān)系，可得擾動位函數(shù)T在局部指北坐標系下沿z方向的梯度分量Tzz為

從上式可看出，若能精確測定重力梯度張量分量Tzz，則可以恢復高精度的地球重力場，得到相應的位系數(shù)和.同時（2）式也意味著，和的不確定度與取決于Tzz的測量噪聲.根據(jù)球諧函數(shù)的正交性，由（2）式得到Tzz的測量噪聲總功率為［17］

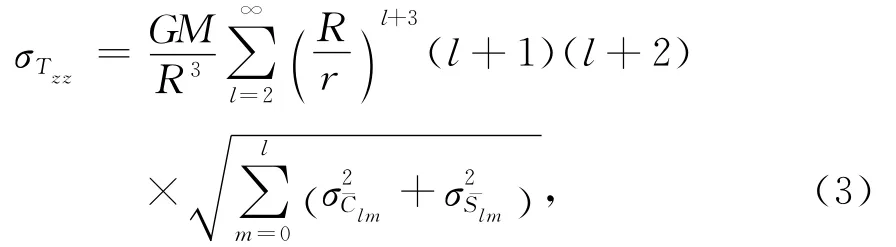
如果已知梯度測量噪聲功率譜密度Szz（f）（單位：E2／Hz），則第l階m次對應頻帶引入的噪聲功率為

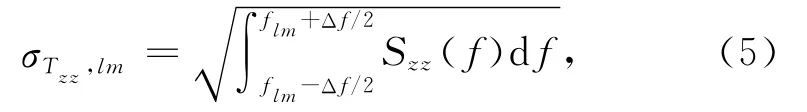
其中flm為第l階m次重力位系數(shù)對應的測量頻率，由傅里葉級數(shù)和球諧系數(shù)的對應關(guān)系來確定［18－19］，Δf為flm對應的測量頻率間隔，取決于測量頻率的分辨率和信號頻率的穩(wěn)定度.重力梯度測量水平或者分辨率取決于測量噪聲的功率譜密度，工程上習慣用噪聲功率譜密度的開方來表示，其單位為E／Hz1／2.若忽略實際重力衛(wèi)星無法覆蓋極軌區(qū)域的影響，同時假定測量頻帶內(nèi)梯度測量噪聲為白噪聲（例如對于GOCE計劃而言，在測量頻帶內(nèi)重力梯度儀噪聲譜密度可看作是白噪聲）.在此假設條件下，再考慮到l階內(nèi)獨立球諧系數(shù)ˉClm和ˉSlm的個數(shù)為（2l＋1），可以得出第l階對應頻帶內(nèi)引入的梯度測量噪聲功率為

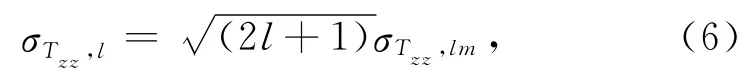
把（5）和（6）式帶入（4）式，整理得到

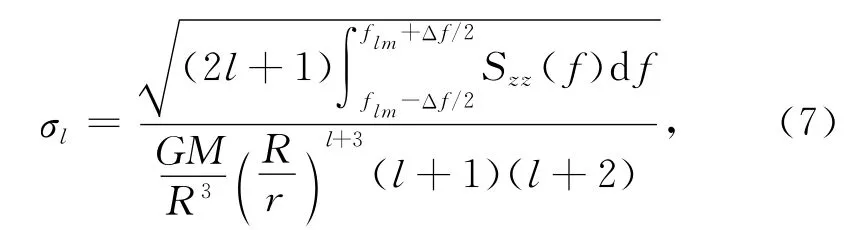
當衛(wèi)星的運行時間為T時，忽略重力信號的時變影響（即忽略信號頻率的漲落影響），則每階次位系數(shù)所對應的梯度測量的頻率間隔為Δf＝1／T［13］，若梯度測量噪聲在測量頻帶內(nèi)為白噪聲，對每階次的影響都為第l階的總貢獻為由（7）式可得到：

為了分析重力位系數(shù)的恢復精度對應的大地水準面起伏和重力異常，我們使用大地水準面累積誤差σN和重力異常累積誤差σΔg評定其影響，表達式分別為［10］

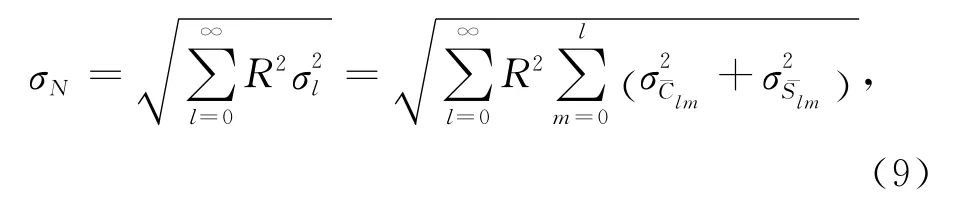
和

3 結(jié)果分析

根據(jù)（8）、（9）和（10）式，我們對不同的梯度測量噪聲功率譜密度、衛(wèi)星高度和衛(wèi)星運行時間的影響進行分析和討論.

3.1 梯度測量精度影響分析

當衛(wèi)星運行時間和高度一定時，重力場恢復精度主要依賴于重力梯度的測量精度.重力梯度測量精度依賴于梯度儀以及衛(wèi)星平臺角速度的測量精度.由（8）式可知，若其它因素不變時，重力梯度測量精度提高N倍，重力場的恢復精度會相應提高N倍.若衛(wèi)星軌道高度H為250km，運行時間T為6個月，梯度測量水平分別為4、7和10mE／Hz1／2，得到相應的誤差階方差估計如圖1所示.需要說明的是，GOCE計劃建議立項前最先確定梯度測量精度為4mE／Hz1／2［3］，GOCE計劃第三次研討會將其調(diào)整為7mE／Hz1／2［20］，GOCE衛(wèi)星在軌運行時重力梯度測量水平約為10mE／Hz1／2甚至更差［20］.另外，本文利用Kaula準則評定恢復重力場位系數(shù)的最大階數(shù)［21］，其具體表達式如下：

圖1 不同梯度測量噪聲情況下的誤差階方差估計Fig.1 Errors degree variance with different precision of gravity gradient measurements

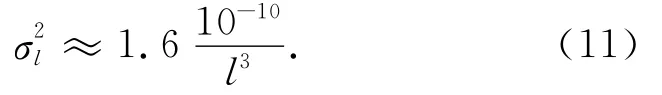
從圖1中可以看到，基于Kaula準則，梯度測量水平為4、7和10mE／Hz1／2所對應的恢復重力場位系數(shù)的最大階數(shù)分別為245、231和221階，這表明提高重力梯度的測量精度可有效提高恢復地球重力場的精度.

相應的大地水準面累積誤差估計如圖2a所示，當階數(shù)為100階時，梯度測量水平為4、7和10mE／Hz1／2所對應的大地水準面精度分別約為0.22、0.39和0.56cm.從150階左右開始大地水準面精度隨階數(shù)升高而明顯地變差，當階數(shù)為200階時，對應的大地水準面精度分別為2.11、3.69和5.27cm.相應的重力異常累積誤差估計如圖2b所示，梯度測量水平為4、7和10mE／Hz1／2，對應前50階的重力異常累積誤差分別為0.0038、0.0067和0.0095mGal，前200階的累積誤差分別為0.59、1.04和1.48mGal.表1給出不同梯度測量噪聲情況下大地水準面累積誤差以及重力異常累積誤差與恢復階數(shù)的關(guān)系.

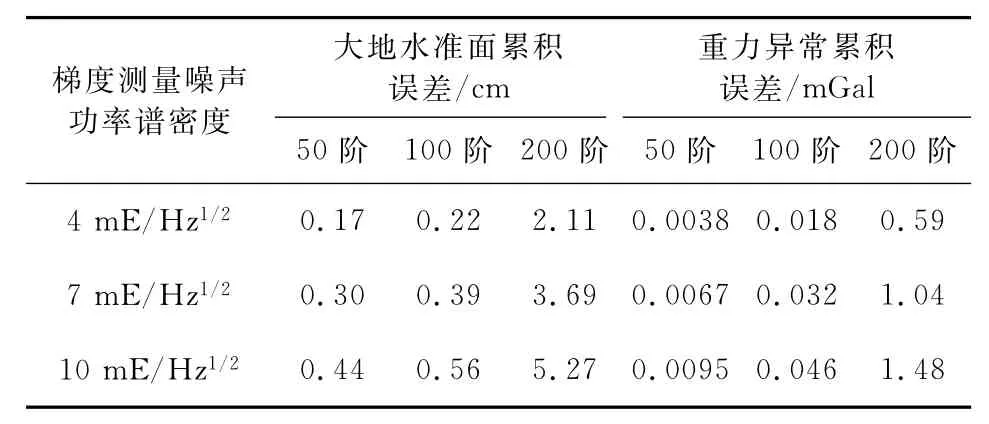
表1 不同梯度測量噪聲情況下的大地水準面累積誤差以及重力異常累積誤差估計比較Table 1 Cumulative geoid height errors and gravity anomaly errors with different precision of gravity gradient measurements

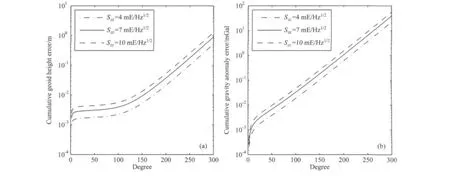
圖2 不同梯度測量噪聲情況下的大地水準面累積誤差（a）以及重力異常累積誤差（b）估計Fig.2 Cumulative geoid height errors（a）and cumulative gravity anomaly errors（b）with different precision of gravity gradient measurements

3.2 衛(wèi)星軌道高度影響分析

軌道高度是重力衛(wèi)星的關(guān)鍵參數(shù)之一，其選擇直接影響到衛(wèi)星重力恢復精度.當衛(wèi)星運行時間和重力梯度測量精度一定時，不考慮大氣密度變化等因素時，降低軌道高度有利于提高恢復重力場的精度.假設在重力梯度測量衛(wèi)星的梯度測量噪聲不變的情況下，梯度測量水平為7mE／Hz1／2，運行時間為6個月，衛(wèi)星軌道高度H分別為200、250和300km，得到相應的誤差階方差估計如圖3所示，重力場位系數(shù)的最大恢復階次數(shù)分別為287、230和191階，即軌道高度每降低50km，恢復重力場系數(shù)的最大階數(shù)提高約40～50階.因此，降低軌道高度可以大幅提高地球重力場恢復的精度和空間分辨率.

相應的大地水準面累積誤差估計如圖4a所示，當階數(shù)小于100階時，恢復的大地水準面精度在不同衛(wèi)星軌道高度情況下差異不大，分別為0.31、0.39和0.58cm，這意味著降低衛(wèi)星軌道高度對階數(shù)小于100階的大地水準面精度的恢復影響較小.隨著階數(shù)增加，降低衛(wèi)星軌道高度對大地水準面精度的恢復有非常大的影響，當階數(shù)為200階時，對應的大地水準面精度分別為0.96、3.69和15.16cm，分別相差約4倍.相應的重力異常累積誤差估計如圖4b所示，從中可得重力異常累積誤差估計隨衛(wèi)星軌道高度增加而變差.由重力異常累積誤差估計同樣可以得到，階數(shù)較低時，衛(wèi)星軌道高度對重力異常的作用不明顯，當軌道高度為200、250和300km時，前50階的重力異常累積誤差分別為0.0050、0.0067和0.0090mGal；而階數(shù)較高時，衛(wèi)星軌道高度的作用隨階數(shù)增加越來越明顯，前200階的重力異常累積誤差分別為0.25、1.04和4.35mGal，也是分別相差約4倍.表2給出了不同高度情況下的大地水準面累積誤差以及重力異常累積誤差估計與恢復階數(shù)的關(guān)系.由此可看出，在衛(wèi)星實際運行條件下，降低衛(wèi)星運行軌道高度有利于提高地球重力場中短波段系數(shù)的恢復精度和空間分辨率.

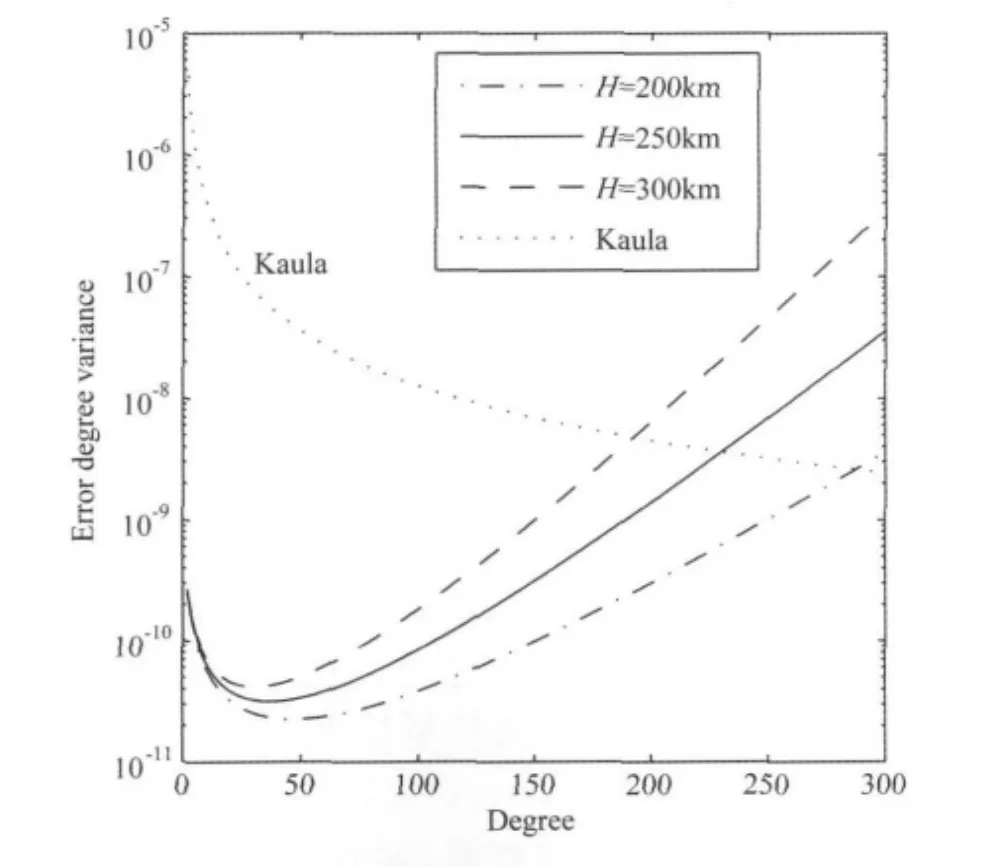
圖3 不同高度情況下的誤差階方差估計Fig.3 Errors degree variance with different altitudes

3.3 衛(wèi)星運行時間影響分析

重力場的恢復精度還取決于衛(wèi)星的運行時間.由（8）式可知，其他因素不變時，衛(wèi)星運行時間延長N倍，靜態(tài)重力場的恢復精度會提高倍.當然，考慮到重力場的時變效應，需選擇合適的運行時間進行模擬分析.若衛(wèi)星軌道高度為250km，梯度測量水平為7mE／Hz1／2，運行時間T為1、3和6個月得到相應的誤差階方差估計如圖5所示，對應恢復重力場位系數(shù)的最大階數(shù)分別為206、222和230階，表明增加運行時間可提高恢復地球重力場的精度.

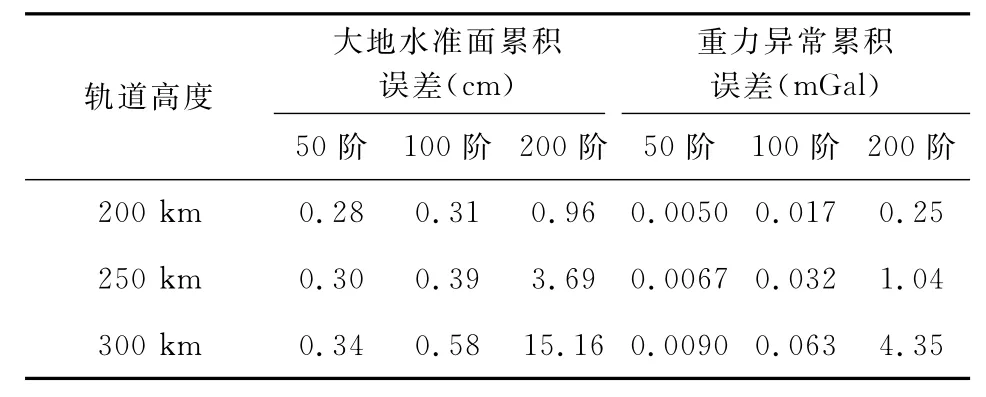
表2 不同高度情況下的大地水準面累積誤差以及重力異常累積誤差估計比較Table 2 Cumulative geoid height errors and cumulative gravity anomaly errors with different altitudes

相應的大地水準面累積誤差估計和重力異常累積誤差估計如圖6a和6b所示，從中可以看出，當階數(shù)為200階時，運行時間為1、3和6個月所對應的大地水準面精度分別為9.04、5.22和3.69cm，重力異常累積誤差估計分別為2.54、1.47和1.04mGal.大地水準面和重力異常恢復精度隨著衛(wèi)星運行時間增加而變好，表3給出了多種運行時間情況下的大地水準面累積誤差以及重力異常累積誤差估計，當重力梯度測量噪聲和衛(wèi)星軌道高度一定時，重力場恢復的空間分辨率依賴于衛(wèi)星的運行時間.值得強調(diào)的是，若考慮到實際情況中重力場的時變效應，衛(wèi)星運行時間進一步增加對地球重力場恢復精度和空間分辨率的改善不會太顯著.

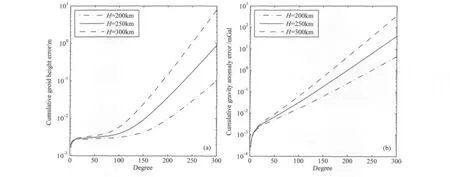
圖4 不同高度情況下的大地水準面累積誤差（a）以及重力異常累積誤差（b）估計Fig.4 Cumulative geoid height errors（a）and cumulative gravity anomaly errors（b）with different altitudes

表3 不同運行時間下的大地水準面累積誤差以及重力異常累積誤差估計比較Table 3 Cumulative geoid height errors and cumulative gravity anomaly errors with different operation duration

圖5 不同運行時間下的誤差階方差估計Fig.5 Errors degree variance with different mission duration

4 討論和結(jié)論

根據(jù)儀器功率譜密度和重力場模型階方差的定義，本文直接建立了梯度測量噪聲功率譜對位系數(shù)恢復精度的表達式，并在此基礎上討論了衛(wèi)星重力梯度測量中儀器技術(shù)指標、衛(wèi)星軌道高度和衛(wèi)星運行時間對重力場恢復的影響.結(jié)果分析表明，重力梯度測量精度越高、衛(wèi)星軌道高度越低以及運行時間越長，恢復地球重力場精度越高.其結(jié)果與國外學者用數(shù)值仿真方法得到的結(jié)果符合很好［10，22－23］.相對于傳統(tǒng)的研究衛(wèi)星重力測量誤差分析和恢復能力論證的方法，本文提出的方法具有簡單和直接等優(yōu)點，且不需要消耗大量計算資源.該方法特別適合項目建議初期對部分觀測量或者載荷指標進行快速評估和確定，也可以對衛(wèi)星重力測量系統(tǒng)數(shù)值模擬仿真中參數(shù)選擇和優(yōu)化設計提供指導.

需要指出的是，在本文的推導中采用的是極圓軌道，而實際重力測量衛(wèi)星的軌道是偏心率很小的橢圓，且軌道的傾角略大于或小于90°，這會導致數(shù)據(jù)采集不能覆蓋極區(qū)以及恢復的重力場模型精度與理想情況有一定偏差.此外，本文僅使用Vzz進行估計，未考慮Vxx和Vyy以及重力梯度衛(wèi)星中衛(wèi)衛(wèi)高低跟蹤模式的貢獻.本文討論中，假設了測量頻帶范圍內(nèi)梯度測量噪聲功率譜密度與頻率無關(guān)，即測量頻帶內(nèi)白噪聲的假設.下一步將對這些問題做進一步分析，特別是實際梯度測量中色噪聲的影響分析.

圖6 不同運行時間下的大地水準面累積誤差（a）以及重力異常累積誤差（b）估計Fig.6 Cumulative geoid height errors（a）cumulative gravity anomaly errors（b）with different operation duration

致 謝 感謝中國科學院測量與地球物理研究所鐘敏研究員、武漢大學測繪學院姜衛(wèi)平教授和徐新禹博士的有益討論，感謝審稿專家提出的修改意見和建議.

（References）

［1］ Reigber C，Balmino G，Schwintzer P，et al.A high－quality global gravity field model from CHAMP GPS tracking data and accelerometry（EIGEN－1S）.Geophysical Research Letters，2002，29：1692.

［2］ Jekeli C.The determination of gravitational potential differences from satellite－to－satellite tracking.Celestial Mechanics and Dynamical Astronomy，1999，75（2）：85－101.

［3］ European Space Agency.Gravity field and steady－state ocean Circulation Exploration Reports for Mission Selection.The Four Candidate Earth Explorer Core Missions，SP－1233（1）.European Space Agency，1999.

［4］ Rummel R，Colombo O L.Gravity field determination from satellite gradiometry.Bulletin Geodesique，1985，59（3）：233－246.

［5］ Reigber C.Gravity field recovery from satellite tracking data.∥SansòF，Rummel R eds.Theory of Satellite Geodesy and Gravity Field Determination.Lecture Notes in Earth Sciences，Vol.25.New York：Springer－Verlag，1989.

［6］ 周旭華，許厚澤，吳斌等.用GRACE衛(wèi)星跟蹤數(shù)據(jù)反演地球重力場.地球物理學報，2006，49（3）：718－723.Zhou X H，Hsu H，Wu B，et al.Earth＇s gravity field derived from GRACE satellite tracking data.Chinese J.Geophys.（in Chinese），2006，49（3）：718－723.

［7］ Han S C，Jekeli C，Shum C K.Efficient gravity field recovery using in situ disturbing potential observables from CHAMP.Geophysical Research Letters，2002，29：1789.

［8］ 徐天河，楊元喜.基于能量守恒方法恢復CHAMP重力場模型.測繪學報，2005，34（1）：1－6.Xu T H，Yang Y X.CHAMP gravity field recovery using energy conservation.Acta Geodaetica et Cartographic Sinica（in Chinese），2005，34（1）：1－6.

［9］ Mayer－Güerr T，Ilk K H，Eicker A，et al.ITG－CHAMP01：A CHAMP gravity field model from short kinematic arcs over a one－year observation period.Journal of Geodesy，2005，78（7－8）：462－480.

［10］ Rummel R，van Gelderen M，Koop R，et al.Spherical Harmonic Analysis of Satellite Gradiometry.Publications on Geodesy，New Series 39，Netherlands Geodetic Commission，1993.

［11］ Schuh W D.Tailored Numerical Solution Strategies for the Global Determination of the Earth＇s Gravity Field.Technical Report，Graz：Technical University Graz，1996.

［12］ Schrama E J O.Gravity field error analysis：Applications of GPS receivers and gradiometers on low orbiting platforms，NASA TM－100769，GSFC Greenbelt Md.20771，1990.

［13］ Sneeuw N.A semi－analytical approach to gravity field analysis from satellite observations.Munich：Technical University of Munich，2000.

［14］ Tscherning C C.Computation of spherical harmonic coefficients and their error estimates using least－squares collocation.Journal of Geodesy，2001，75（1）：12－18.

［15］ Baur O，Austen G，Kusche J.Efficient GOCE satellite gravity field recovery based on least－squares using QR decomposition.Journal of Geodesy，2008，82（4－5）：207－221.

［16］ Gruber C，Novák P，Sebera J.FFT－based high－performance spherical harmonic transformation.Studia Geophysica et Geodaetica，2011，55（3）：489－500.

［17］ Ilk K H，F(xiàn)lury J，Rummel R，et al.Mass transport and mass distribution in the earth system.Proposal for a German Priority Research Program，GeoForschungs Zentrum Potsdam.2004.

［18］ Kazhdan M，F(xiàn)unkhouser T，Rusinkiewicz S.Rotation invariant spherical harmonic representation of 3Dshape descriptors.∥Proceedings of the 2003Eurographics／ACM SIGGRAPH Symposium on Geometry Processing.Aachen，Germany：Eurographics Association Press，2003：156－16.

［19］ Novotni M，Klein R.3DZernike descriptors for content based shape retrieval.∥Proceedings of the Eighth ACM Symposium on Solid Modeling and Applications.Washington，USA：ACM Press，2003：216－225.

［20］ Drinkwater M R，Haagmans R，Muzi D，et al.The GOCE Gravity Mission：ESA′s First Core Earth Explorer.Proceedings of 3rd International GOCE User Workshop，6－8 November，2006，F(xiàn)rascati，Italy，ESA SP－627，ISBN 92－9092－938－3，2007：1－8.

［21］ Kaula W M.Theory of Satellite Geodesy.Massachusetts：Blaisdell Publishing Company Press，1966：34－35.

［22］ Koop R.Global gravity field modelling using satellite gravity gradiometry.Publications on Geodesy，New Series 38，Netherlands Geodetic Commission，1993.

［23］ Schrama E J O.Gravity field error analysis：applications of global positioning system receivers and gradiometers on low orbiting platforms.Journal of Geophysical Research，1991，96（B12）：20041－20051.

Spectral analysis for recovering the Earth′s gravity potential by satellite gravity gradients

CAI Lin1，3，ZHOU Ze－Bing2，3＊，ZHU Zhu2，3，GAO Fang2，3，HSU Houtse3，4
1 Department of Electronics and Information Engineering，Huazhong University of Science and Technology，Wuhan 430074，China
2 School of Physics，Huazhong University of Science and Technology，Wuhan 430074，China
3 Institute of Geophysics，Huazhong University of Science and Technology，Wuhan 430074，China
4 Institute of Geodesy and Geophysics，Chinese Academy of Sciences，Wuhan 430077，China

Direct relationship between the power spectrum density of the satellite gradiometry and the coefficients of the Earth′s gravity potential is established based on the definitions of the instrument′s power spectrum density and the Earth′s gravity field potential，and then the effect of gravity gradient measurement accuracy，the altitude of the satellite，and the operation duration on recovering of Earth＇s gravity field is analyzed by using this method.This method is simple and direct compared with the others based on the least square approach，and is very useful to design and verify the parameters for the Earth gravity recovery missions.

Satellite gravity gradiometry，The Earth＇s gravity potential，Spectral analysis

10.6038／j.issn.0001－5733.2012.05.014

P228

2011－10－18，2011－11－27收修定稿

國家自然科學基金項目（11075058）資助.

蔡林，男，1984年生，在讀博士研究生，主要從事衛(wèi)星重力測量方法研究.E－mail：mumu0202＠gmail.com

＊通訊作者周澤兵，男，1973年生，教授，主要從事衛(wèi)星重力測量和引力實驗研究.E－mail：zhouzb＠m(xù)ail.hust.edu.cn

蔡林，周澤兵，祝竺等.衛(wèi)星重力梯度恢復地球重力場的頻譜分析.地球物理學報，2012，55（5）：1565－1571，

10.6038／j.issn.0001－5733.2012.05.014.

Cai L，Zhou Z B，Zhu Z，et al.Spectral analysis for recovering the Earth′s gravity potential by satellite gravity gradients.Chinese J.Geophys.（in Chinese），2012，55（5）：1565－1571，doi：10.6038／j.issn.0001－5733.2012.05.014.

（本文編輯 胡素芳）