課堂教學評估的多層次貝葉斯網絡分類器方法

李蘭春，王雙成，王 輝

（1.上海立信會計學院外語學院，上海 201620；2.上海立信會計學院數學與信息學院，上海 201620；3.中央民族大學信息工程學院，北京 100081）

課堂教學評估的多層次貝葉斯網絡分類器方法

李蘭春1，王雙成2，王 輝3

（1.上海立信會計學院外語學院，上海 201620；2.上海立信會計學院數學與信息學院，上海 201620；3.中央民族大學信息工程學院，北京 100081）

課堂教學是為實現一定的教學目標而展開的信息傳遞、過程控制和策略實施過程.依據課堂教學的特點給出了課堂教學評估的指標體系，并在此基礎上建立了課堂教學評估的層次貝葉斯網絡分類器模型.為提高分類器的分類識別準確率，在連續屬性中引入形狀參數，實驗結果顯示，通過形狀參數的優化能夠顯著提高分類器的分類識別可靠性.

課堂教學；樸素貝葉斯網絡；分類器；評估

0 引言

課堂教學是為實現一定的教學目標，通過信息傳遞、過程控制和策略實施而展開的師生之間的雙邊活動.［1－2］課堂教學已經具有悠久的歷史，在相當長的一段時間內仍將是一種主要的教學方式，也是學生建立知識結構、發展認知結構和人格形成的主要途徑.課堂教學質量評估能夠為制定更科學的教學策略提供具有針對性的信息，有助于推動教學改革和提高教學質量.目前課堂教學評估主要采用三級指標體系［3－4］，在指標之間具有線性關系的假設下，根據三級指標計算出二級指標，再由二級指標最終確定一級指標的等級.這一等級判斷過程是一個層次分類問題（模擬人類概念學習與應用的技術），而且基于分類器的課堂教學質量等級判斷不需要線性關系的假設，因此在評價的可靠性方面具有優勢，并可開拓課堂教學評估的新思路.

現在已經有了許多著名的分類器，如神經網絡、支持向量機、決策樹、統計判別分析和貝葉斯網絡等，它們在許多領域得到了廣泛的應用.但這些分類器往往都需要許多例子數據進行學習.課堂教學方面的例子數據一般比較少，而且其中的連續數據也不適合于離散化（離散化會丟失過多的信息）.樸素貝葉斯網絡（naive Bayesian network，簡記為NBN）［5－6］分類器是目前最適合于小例子集分類預測的概率分類器，這種分類器不需要許多例子數據用于訓練，并且能夠直接處理連續屬性.在樸素貝葉斯網絡分類器中處理連續屬性的核心問題是條件密度估計，目前主要采用兩種方式來估計條件密度［7－8］：一種是使用高斯函數來估計屬性條件密度，而高斯函數可能與實際密度函數有較大的差距，從而影響分類器的分類準確性；另一種是采用高斯核函數估計屬性條件密度，高斯核函數又易于導致對例子的過度擬合，也同樣會降低分類器的泛化能力.

本文從課堂教學的信息傳遞、過程控制和教學策略三個方面來制定課堂教學質量評估的指標體系，并針對課堂教學質量評估的實際情況和需求建立多層次樸素貝葉斯網絡（mult－hierarchical naive Bayesian network，簡記為MHNBN）分類器模型.為避免使用高斯核函數估計屬性條件密度可能導致的對例子過度擬合問題，在高斯核函數中引入形狀參數，并通過形狀參數的優化來提高分類器的分類識別準確性.

1 MHNBN分類器學習

MHNBN分類器學習包括結構學習和參數學習兩部分.結構學習一般是依據專家的領域知識確定指標之間的層次關系；參數學習是使用例子數據進行邊緣和條件概率估計，以及在某種分布假設下的連續屬性條件密度估計.

1.1 MHNBN分類器結構

NBN分類器基于這樣的假設：當類變量給定時，屬性變量之間條件獨立.這一假設決定了NBN分類器結構是星形結構.MHNBN分類器是NBN分類器的層次組合，下面給出標準NBN分類器結構（用S表示）和一個三層次MHNBN分類器的層次樹，如圖1所示.

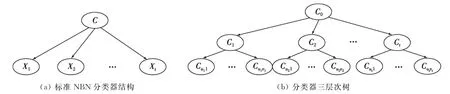
圖1 NBN分類器結構和分類器層次樹

在圖1（a）的標準NBN分類器結構中，類結點是所有屬性結點的唯一父結點；圖1（b）是將NBN分類器作為一個結點而得到的MHNBN分類器層次結構樹，將圖1（b）的上面兩層展開后的分類器結構如圖2所示.

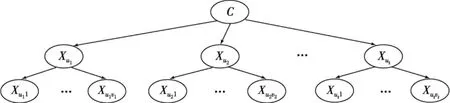
圖2 展開后的兩層次分類器結構

1.2 MHNBN分類器參數學習

MHNBN分類器參數學習是依據例子數據估計概率和密度的過程，以圖2所示的兩層次分類器（分別稱為上層分類器和下層分類器）為例給出參數學習方法.在由一級和二級指標構成的上層分類器中，C和X u1，…，X ut都是離散指標變量；而由二級和三級指標構成的下層分類器中，底層指標X u11，…，X u1v1，X u21，…，X u2v2，…，X ut1，…，X utvt可以是離散或連續指標.

1.2.1 一級和二級指標邊緣概率估計

采用最大似然估計方法，那么，一級和二級指標需要估計邊緣概率（先驗概率）.

一級指標邊緣概率估計：

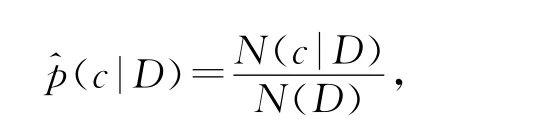
其中N（c｜D）為例子數據集D中第c類（C＝c）的例子數量，N（D）為所有例子數量.

二級指標邊緣概率估計：

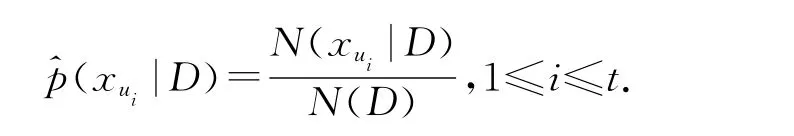
其中N（x ui｜D）為例子數據集D中第x ui類（X ui＝x ui）的例子數量.

1.2.2 二級和三級指標條件概率或密度估計

對于非葉子結點的二級或三級指標，只需要估計條件概率；而對作為葉子結點的二級或三級指標可能要估計條件概率（離散指標）和條件密度（連續指標）.

二級離散指標的條件概率估計：

其中N（x ui，c｜D）為第c類中X ui＝x ui的例子數量.

三級離散指標的條件概率估計：

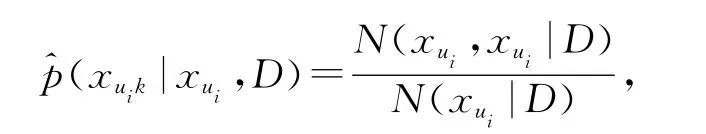
其中N（x ui k，x ui｜D）為第x ui類中X uik＝x uik的例子數量.

三級連續指標的條件密度估計：

2 MHNBN分類器表示形式與分類過程

以兩個層次的MHNBN分類器為例，給出MHNBN分類器的表示形式和分類過程.基于貝葉斯網絡理論和貝葉斯公式，以及圖2中所體現的條件獨立性關系，可得：

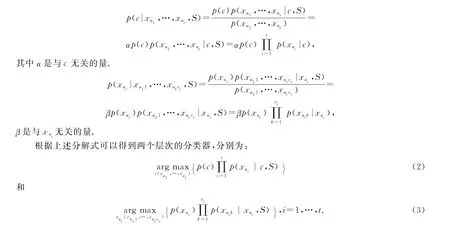
分類過程是：首先由下層分類器確定二級指標X u1，…，X ut的值，然后再基于上層分類器得到一級指標的值.多層次分類器的分類也是這樣的自下而上的過程.

3 課堂教學評估

首先建立課堂教學評估指標體系，然后結合指標體系與例子數據便能夠建立MHNBN分類器，并基于MHNBN分類器進行課堂教學評估.

3.1 課堂教學評估指標體系

指標體系是進行課堂教學評估的前提，依據教育控制論、系統科學原理和課堂教學機制等建立一個課堂教學評估三級指標體系，也可根據實際需要對指標體系進行層次擴展.

（1）一級指標

課堂教學等級（C）分4個級別，分別是：A級（優秀），B級（良好），C級（一般），D級（較差）.

（2）二級指標

課堂教學所屬的二級指標是：課堂信息傳遞（X1），課堂教學控制（X2），課堂教學策略（X3）.它們都分三個等級，分別是A級（好），B級（中）和C級（差）

（3）三級指標

課堂信息傳遞所屬的三級指標：教師向學生的信息傳遞（語法信息傳遞（X11），語義信息傳遞（X12），語用信息傳遞（X13）），學生向教師的信息傳遞（反饋信息（X14），前饋信息（X15），退饋信息（X16））.

課堂教學控制所屬的三級指標：知識結構控制（概念（X21），規則（X22），問題解決（X23）），認知結構控制（認知操作（X24），動力供給（X25），認知策略（X26）），方式控制（程序控制（X27），隨機控制（X28））.

課堂教學策略所屬的三級指標：講授式教學（X31），啟發式教學（X32），演繹式教學（X33），概括式教學（X34），回溯式教學（X35）.

3.2 課堂教學評估的分類器模型

根據上面的課堂教學評估指標體系可得到兩層次的MHNBN分類器結構，如圖3所示.

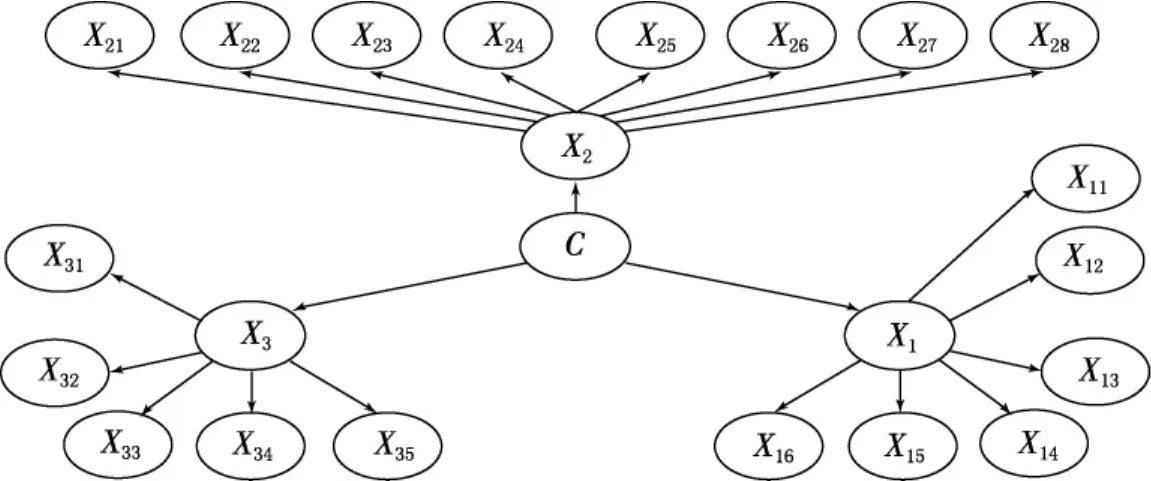
圖3 用于課堂教學評估的MHNBN分類器結構

基于分類器結構和例子數據進行參數估計，從而得到用于課堂教學評估的MHNBN分類器，輸入最新課堂教學信息，通過分類運算便可獲得課堂教學的等級.

3.3 NBN分類器可靠性實驗與分析

在UCI機器學習數據倉庫［9］中選擇12個具有連續屬性的分類數據集，分別使用對連續屬性離散化（DNBN）、高斯密度估計（GNBN）、高斯核密度估計（GKNBN）和引入形狀數的高斯核密度估計（GKSNBN）而得到的NBN分類器進行分類預測，采用10折交叉有效性（10－fold cross－validation）驗證方法進行分類器的分類準確性估計，如表1所示.

表1 分類預測準確率比較

從表1中可以看出，DNBN分類器具有良好的分類準確率，而GKNBN分類器要優于DNBN和GNBN分類器，GKSNBN分類器還要優于GKNBN分類器.這表明使用把DNBN分類器和GKSNBN分類器層次組合而得到的MHNBN分類器，進行課堂教學評估等級判斷將是比較可靠的.

4 小結

根據教育控制論、系統科學原理和課堂教學機制等給出了一個課堂教學評估的三級指標體系，在此基礎上，具有針對性地建立了用于課堂教學評估的動態層次樸素貝葉斯網絡分類器.為提高分類器層次組件的分類準確性，在連續屬性的條件密度估計中引入了形狀參數，并通過形狀參數的優化來提高分類器的泛化能力，實驗結果顯示，形狀參數的優化能夠顯著提高分類器的分類準確性，這表明將其用于課堂教學質量評估，所得到的評估識別結果會更加可靠.

［1］王黎.應用型本科經濟學課堂教學改革探索［J］.教育探索，2010，1：64－65

［2］楊金觀，聶建峰.課堂教學質量評價——一個在高校實際工作中被誤解的概念［J］.高教發展與評估，2010，1：15－20.

［3］陳弘，李幽錚，鄭鋼.基于AHP法的教師教學質量評估改進模型［J］.金陵科技學院學報，2010，26（1）：31－34.

［4］劉香芹，陳俠.模糊多層次多屬性高校教師教學質量評估［J］.沈陽航空工業學院學報，2010，27（2）：90－92.

［5］RAMONI M，SEBASTIANI P.Robust Bayes classifiers［J］.Artificial Intelligence，2001，125（1／2）：209－226.

［6］JING Y S，PAVLOVI C＇V，REHG J M.Boosted Bayesian network classifiers［J］.Machine Learning，2008，73（2）：155－184.

［7］JOHN G H，LANGLEY P.Estimating continuous distributions in Bayesian classifiers.［C］／／Proceedings of the 11th International Conference on Uncertainty in Artificial Intelligence，Bec Canada：Qu ＆Eacute，1995：106－143.

［8］PéREZ A，LARRANAGA P，INZA I.Bayesian classifiers based on kernel density estimation［J］.International Journal of Approximate Reasoning：Flexible Classifiers，2009，50（2）：341－362.

［9］MURPHY S L，AHA D W.UCI repository of machine learning databases［EB／OR］.［2009－12－04］.http：／／www.ics.uci.edu／～mlearn／MLRepository.Html.

The method of mult－hierarchical Bayesian network classifier for classroom teaching assessment

LI Lan－chun1，WANG Shuang－cheng2，WANG Hui3

（1.School of Foreign Studies，Shanghai Lixin University of Commerce，Shanghai 201620，China；2.School of Mathematics and Information，Shanghai Lixin University of Commerce，Shanghai 201620，China；3.School of Information Engineering，The Central University for Nationalities，Beijing 100081，China）

The classroom teaching is a process of teaching information transfer，classroom control and implementation of teaching strategies for realizing certain educational objectives.A index system of classroom teaching assessment is presented based on the features of classroom teaching.And a model of mult－hierarchical naive Bayesian network classifier is developed for classroom teaching assessment.In order to improve the classification accuracy of classifier，the shape parameter is pulled in continuous attributes.Experimental results show that the reliability of classifier can be significantly improved by shape parameter optimization.

classroom teaching；naive Bayesian network；classifier；assessment

TP 181

520·20

A

1000－1832（2012）01－0050－05

2011－02－04

國家自然科學基金資助項目（60675036）；教育部人文社科基金資助項目（10YJA630154）；上海市教委重點學科建設項

目（J51702）；上海市教委科研創新重點項目（09zz202）.

李蘭春（1959—），女，講師，主要從事教育原理與評估研究；王雙成（1958—），男，博士，教授，主要從事智能數據處理研究；王輝（1961—），男，碩士，教授，主要從事決策支持技術研究.

陶 理）