盾構掘進速度及非正常停機對地面沉降的影響

林存剛 ，吳世明，張忠苗 ，劉俊偉 ，李宗梁

（1. 浙江大學 巖土工程研究所，杭州 310058；2. 浙江大學 軟弱土與環境土工教育部重點實驗室，杭州 310058； 3. 杭州慶春路過江隧道有限公司，杭州 310002）

1 引 言

近些年，隨國內地鐵及水底隧道建設熱潮的興起，盾構法隧道施工技術越來越廣泛地在全國各大中城市應用。盾構隧道多穿越城市建筑物及地下管線密集區域，對隧道施工引起的地層位移控制較為嚴格，因此，國內外眾多學者對于盾構隧道施工引起的地層位移進行了廣泛深入的研究，主要有經驗公式法[1－3]、解析法[4－8]、模型試驗法[9]及數值模擬法[10]等。這些研究考慮了施工方法、地層條件、隧道埋深及直徑、盾構掘進參數的控制等多種因素對地面沉降的影響。然而，盾構掘進速度及非正常停機對盾構隧道施工引起的地面沉降的影響研究，國內外文獻中鮮有報道。

本文由盾構掘進速度及停機時間確定盾構壓重在其下臥土層中產生的附加應力的持續時間后，運用太沙基一維固結理論和單向壓縮分層總和法計算在該作用時間內的沉降，應用Peck 公式建立起盾構下臥土層沉降與地面沉降的關系，并以杭州慶春路過江隧道地面沉降的實測數據對該理論進行了驗證。

本文僅考慮盾構掘進速度及非正常停機時間對盾構隧道施工引起的地面沉降的影響，對隧道開挖基底土體回彈、掘進參數控制等其他因素不加以考慮。

2 相關研究

Rowe 等[6]、Clough 等[11]對美國第1 條土壓平衡盾構隧道施工引起的地面沉降分析認為，盾構長時間在某一斷面擱置，會加劇該斷面的地面沉降。盾構離開監測斷面5 個月之后的隧道軸線位置地面沉降如圖1 所示[6,11]。

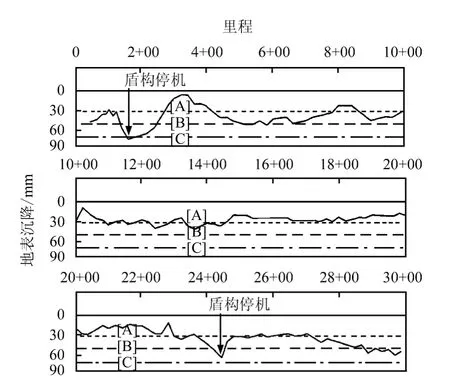
圖1 隧道軸線位置地面沉降 Fig.1 Surface settlement profile along centerline of tunnel alignment

由圖1 可見，沿隧道軸線位置里程1+60 和24+50 附近地面沉降最大，約為76 mm。盾構在里程1+160 位置停留15 d 進行動力系統與盾構機的連 接；盾構穿越木樁后有大量木屑殘留在刀盤縫隙中，在里程24+50位置停留進行清理。Clough等[11]認為，該兩處位置發生較大地面沉降和盾構在這兩處長時間停留有關。

Rowe 等[6]認為，盾構停機時，由于土體的固結或水土壓力的重分布，盾構土倉壓力逐漸減少，由此引起較大的開挖面地層損失，進而加劇地面沉降。

除此[6,11]之外，鮮有關于盾構掘進速度及非正常停機對地面沉降的影響研究，并缺少相關的理論解釋。

筆者認為，盾構長時間停機導致地面沉降加劇的原因，除盾構切口壓力損失引起開挖面地層損失外，還有盾構壓縮下臥土層引起固結沉降，該固結沉降持續時間由盾構掘進速度和停機時間確定。

3 計算模型的建立及求解

3.1 盾構下臥土層沉降計算

盾構在地層中掘進，計算模型縱剖面如圖2 所示。

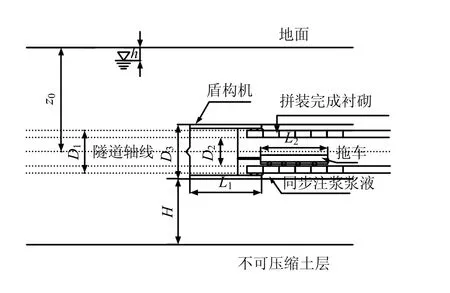
圖2 盾構地層中掘進計算模型（縱剖面） Fig.2 Calculation model of shield tunnelling in soils（longitudinal profile）

如圖2 所示，盾構在地層中掘進，z0為隧道軸線埋深(m)，D1為隧道外徑(m)，D2為隧道內徑(m)；D3為盾構機外徑（開挖直徑）(m)，L1為盾構機主機長(m)，L2為拖車長(m)，L 為盾構主機和拖車總長(m)，L=L1+L2，Wshield為盾構主機和拖車總重(kN)；h 為地下水位位于地表以下的深度(m)，H 為盾構機底部距離不可壓縮土層（卵石層、碎石層或基巖）的長度(m)；假定自地面至不可壓縮土層為均一地層，rsoil為土體重度(kN/m3)；rlining為襯砌管片重度(kN/m3)，rgrout為同步注漿漿液重度(kN/m3)，rw為地下水重度(kN/m3)。

圖2 計算模型對應橫斷面見圖3。

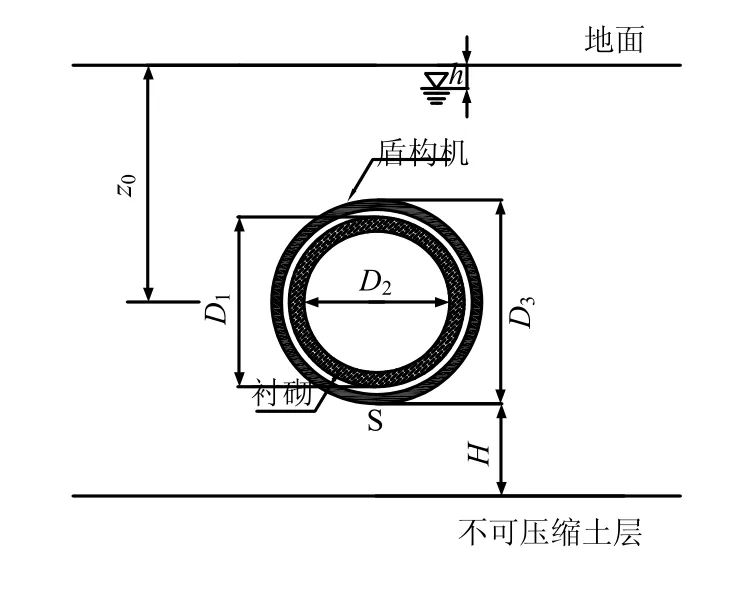
圖3 盾構地層中掘進計算模型（橫斷面） Fig.3 Calculation model of shield tunnelling in soils（transverse section）

Verruijt 等[12]認為，由于建成隧道的重量小于開挖土體的重量，會在隧道底部產生“浮力效應”，該“浮力效應”會對隧道開挖引起的地面沉降產生影響。通過建立隧道在均質各向同性土體中開挖的彈性半平面模型，僅考慮地層損失和“浮力效應”，通過復變函數方法求解得出隧道開挖引起的橫斷面地面沉降。計算結果顯示，“浮力效應”會對隧道開挖引起的地面沉降產生影響，建成隧道相對于開挖土體越輕，地面沉降將越小，且橫向地面沉降槽寬度較僅考慮地層損失時計算所得沉降槽要窄；考慮“浮力效應”后，計算所得沉降槽與實測值更吻合。Verruijt 等的分析不考慮擾動土體固結，土體發生彈性變形，瞬時完成，與時間因素無關。

筆者認為，不僅開挖土體與建成隧道的重量差會對隧道開挖引起的地面沉降產生影響，而且盾構與建成隧道的重量差也會對其產生影響，且該影響與盾構掘進速度和停機時間相關。

不計擾動土體超孔隙水壓力的消散，僅考慮開挖出土體與盾構及成型管片重量差引起的盾構下臥土體的應力釋放，短期內盾構機底部S 位置（見圖3）土體有效應力經歷了4 個階段：

（1）應力狀態0 為初始應力狀態0σ

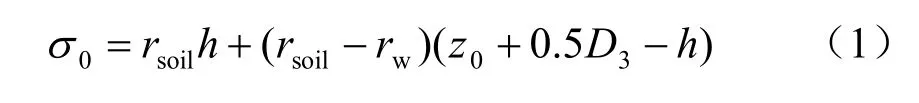
（2）應力狀態1 為土體挖出后土應力1σ

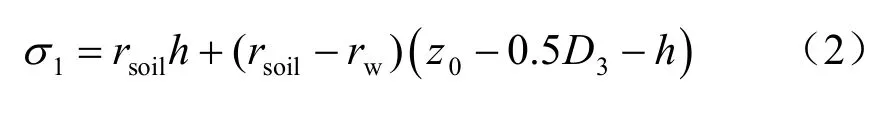
（3）應力狀態2 為盾構機置換開挖出土體后土應力2σ

盾構機置換土體重量為Wsoil

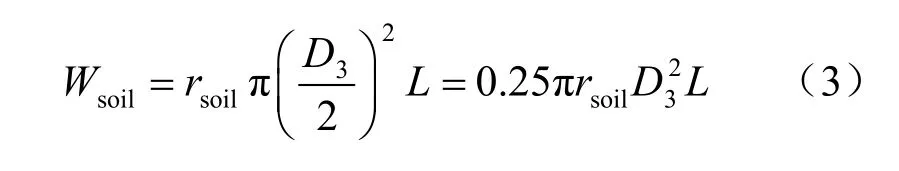
定義盾構機與其置換土體重量比為1λ ：

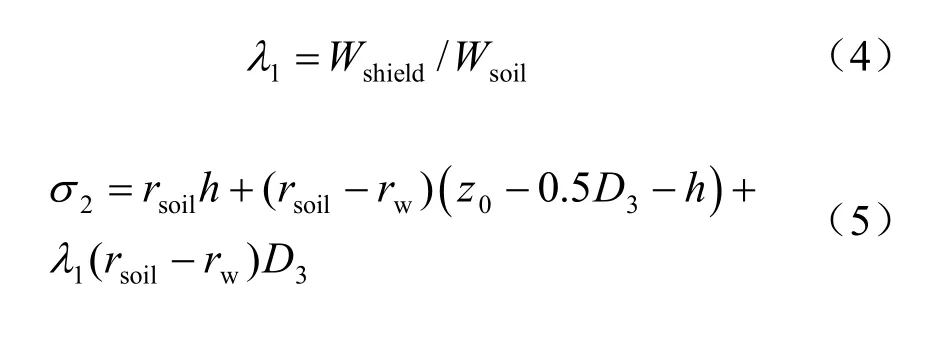
（4）應力狀態3 為盾尾脫離，拼裝成型管片和同步注漿漿液置換開挖出土體后土應力3σ

拼裝成型管片和同步注漿漿液沿隧道軸線方向L 長度重量為Wlining：

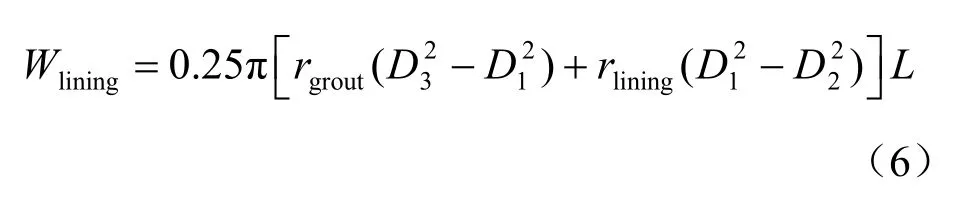
定義拼裝成型管片和同步注漿漿液重量與其置換土體重量比為2λ ：

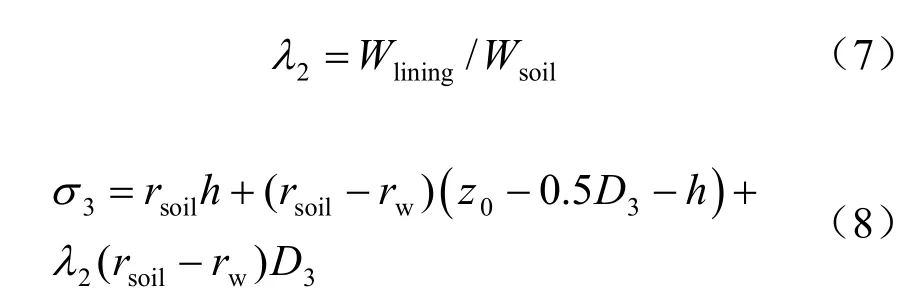
由于盾構機的重量及拼裝成型管片和同步注漿液的重量與置換出的土體重量不相等，即 λ1≠1，λ2≠1，所以盾構通過以及離開時，對其底部土體加載或卸載，土體瞬時發生彈性壓縮或回彈。該土體變形瞬時完成，可由彈性理論近似求得，與時間因素無關，與上述各有效應力狀態維持時間長短無關，因此，與盾構掘進速度及停機時間相關性不大。盾構掘進速度及停機時間不影響隧道下臥土層因加載或卸載（應力狀態σ0轉化為σ1，再轉化為σ2，最后轉化為 σ3）引起的土體彈性變形，因此，本文研究盾構掘進速度及停機對地面沉降的影響時，未考慮盾構底部土體因加載或者卸載引起的土體彈性變形。

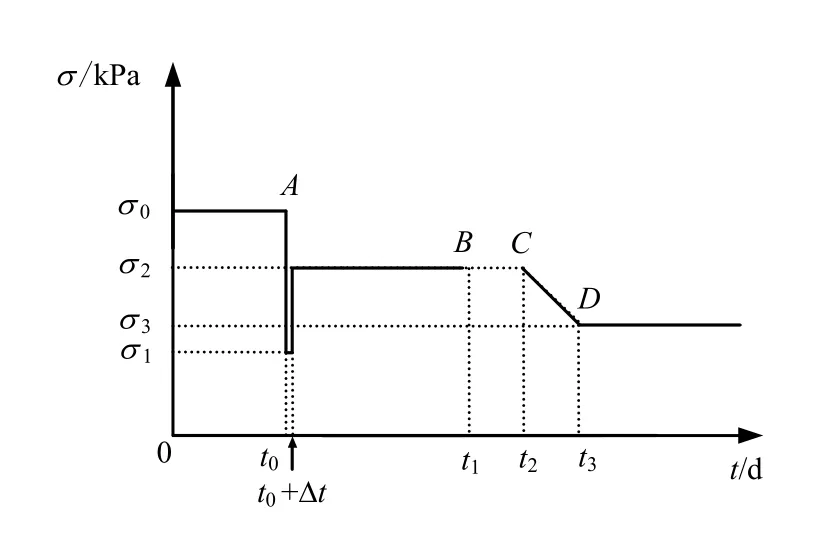
圖4 盾構底部土體有效應力變化 Fig.4 Changes of effective soil stresses beneath the shield

圖4 表示任一斷面X 盾構底部S 位置土體有效應力隨盾構機掘進的變化。圖中，t0時刻盾構切口到達該斷面，t2時刻盾構拖車尾部離開該斷面。

圖中Δt 相對較小，忽略不計。

考慮到附加應力的擴散，盾構拖車離開X 斷面時，其隧道下臥土層仍受到盾構壓重的影響；假定隨著盾構逐漸遠離土體有效應力線性遞減，至拖車尾部離開10 m 盾構壓重的影響已完全消失。即圖4中，t3時刻對應拖車尾部離開X 斷面10 m。

圖4 中虛線段BC 對應盾構在X 斷面停機時間tstop。

設盾構通過X 斷面前后掘進速度為v(m/d)，則：

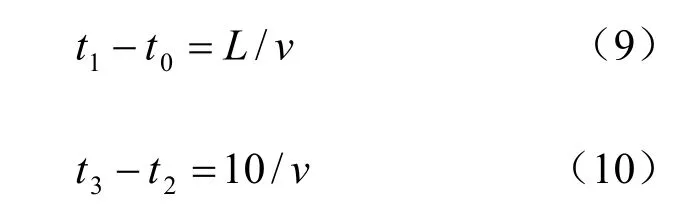
為簡化計算，圖4 轉化為圖5。

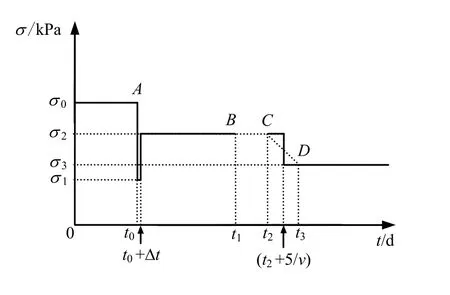
圖5 盾構底部土體有效應力變化(簡化后) Fig.5 Changes of effective soil stresses beneath the shield（simplified）

X 斷面2σ 持續時間 2tσ：

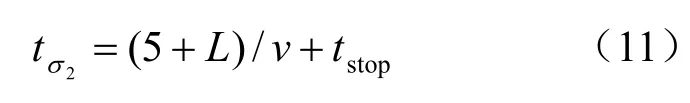
土體經開挖，由初始應力狀態0σ 轉變為1σ ，隨后盾構壓重相對于 1σ 應力狀態施加附加應力2σΔ ；盾構遠離后管片拼裝完畢，管片壓重相對于1σ 應力狀態施加附加應力 3σΔ 。由 2σΔ 和 3σΔ 共同作用t 時間段下盾構下臥土層沉降St：

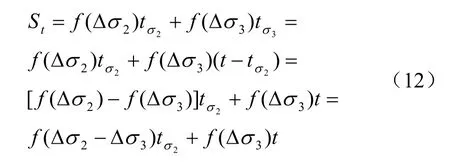
式中：f (Δ σi)tσi為附加應力 Δσi相對于應力狀態σ1作用時間 tσi產生的土體沉降，i=2、3；[ f ( Δσ2)- f (Δ σ3)]tσ2表示 tσ2時間段內附加應力 Δσ2與 Δσ3相對于應力狀態 σ1壓縮盾構下臥土層產生的土體沉降差，等價于 tσ2時間段內附加應力 Δσ2與 Δσ3之差相對于應力狀態 σ1壓縮盾構下臥土層產生的土體沉降，即 [ f (Δ σ2-Δσ3)]tσ2，亦等價于 tσ2時間段內應力狀態 σ2相對于應力狀態 σ3產生的附加應力壓縮盾構下臥土層產生的土體沉降。

由式（12）可見，從盾構切口到達開始，任意時刻t某一斷面盾構下臥土層的沉降，僅與 2tσ相關，即應力狀態2σ 持續時間。而由式（11）可見，2tσ取決于盾構掘進速度和停機時間。

一般情況下，Wshield>Wlining，故2σ >3σ ，相對于3σ 應力狀態，2σ 應力狀態相當于對盾構底部土體施加附加荷載Wload：

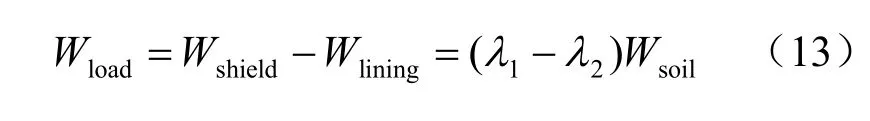
假定Wload均勻作用于盾構機在其底面投影面上，如圖6 所示。

圖中，Pload=Wload/(LD3)。盾構沿隧道軸線方向掘進，圖中矩形分布荷載以速度v 沿盾構前進方向移動。對于任一X 斷面盾構底面土體附加應力及沉降的計算，考慮到圖中矩形荷載將移動通過X 斷面前后，掘進速度均衡的情況下，各個斷面先后經歷的應力狀態基本相同，因此，可將圖6 所示計算模型進行簡化，將矩形均布荷載轉化為條形均布荷載。轉化后計算模型如圖7 所示。

Mindlin[13]給出豎向點荷載作用在彈性半無限空間內部時的應力彈性解；在Mindlin 解基礎之上，Skopek[14]和Poulos 等[15]推導得到條形均布荷載作用在彈性半無限空間內部時豎向應力的彈性解，見式（14），其計算模型見圖8。

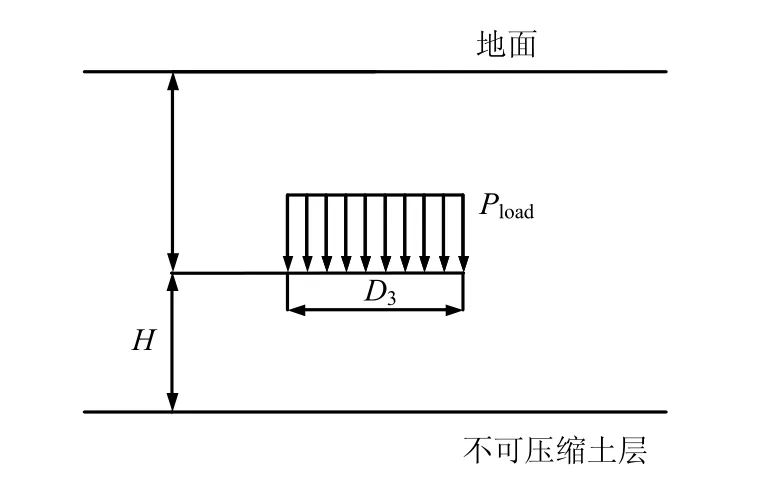
圖7 盾構機底面土體附加荷載示意圖（簡化后） Fig.7 Additional loads imposed on soils beneath the shield（simplified）

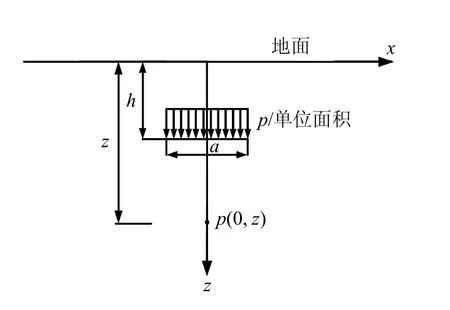
圖8 彈性半無限空間內部作用條形荷載 Fig.8 Strip load inside a semi-infinite mass

當x =0時

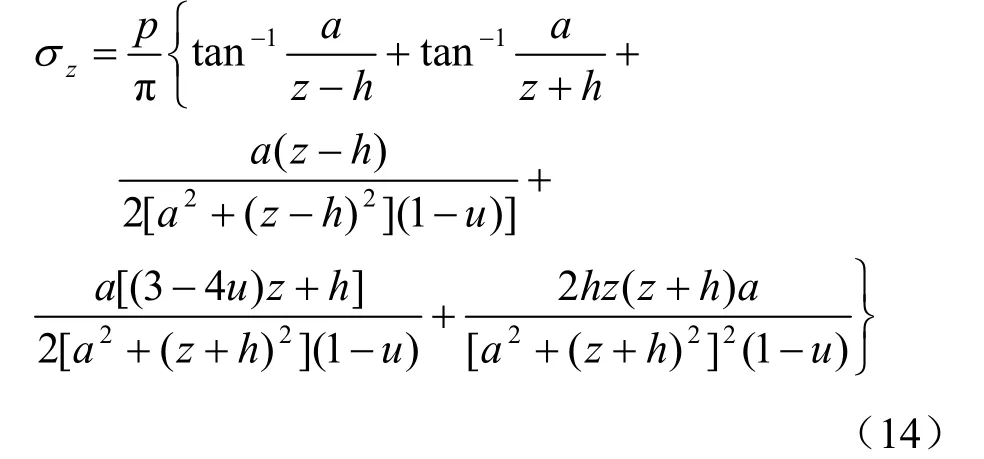
式中：u 為土體泊松比；zσ 為圖中P 點豎向附加應力。

將圖7 所示計算模型代入式（14），即可得盾構下臥土體軸線位置深度z 處豎向附加應力 σz。

計算得出盾構下臥土層 σ2狀態相對于 σ3狀態的附加應力之后，在獲取計算范圍內土體的初始孔隙比、壓縮系數等參數后，采用單向壓縮分層總和 法[16]即可算得盾構下臥土體因盾構產生的附加應力壓縮下臥土層產生的總固結沉降Sc。

在盾構產生的附加應力作用下，其下臥土體排水固結，引述太沙基一維固結理論[16－17]：

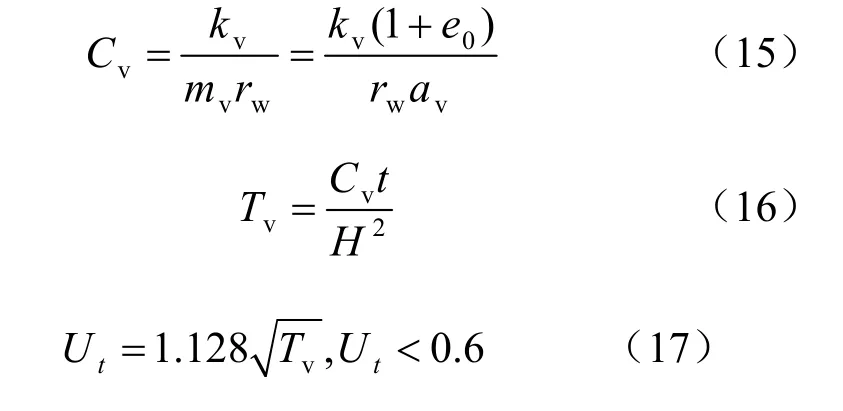
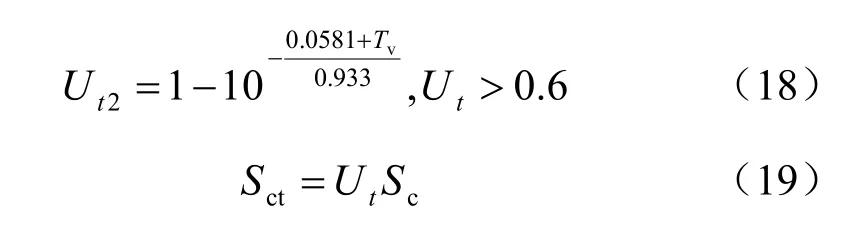
式中：Cv為固結系數（m2/s）；kv為豎向滲透系數（m/s）；mv為體積壓縮系數（kPa-1）；rw為水的重度（kN/m3）；av為豎向壓縮系數（kPa-1）；e0為土體初始孔隙比；Tv為豎向固結時間因子，無量綱；t 為固結沉降歷時（s）；H 為地基土層的最大豎向排水距離（m），對于雙面排水為土層厚度的一半，單面排水為土層厚度；Ut為t 時刻平均固結度；Sct為地基t 時刻的主固結沉降（mm）；Sc為地基的總固結沉降（mm）。

獲得盾構下臥土層的初始孔隙比、滲透系數、壓縮系數等參數后，代入式（15）～（19），即可得到任意時刻t 的固結沉降。

式（11）給出了盾構產生的附加荷載對下臥土層的作用時間，與式（15）～（19）聯立，則可算得相對于3σ 狀態，在盾構產生的附加應力作用下其下臥土層產生的固結沉降Sct。

3.2 地面沉降計算

盾構機作為一個剛性體，認為其整體位移Sshield與其下臥土層固結沉降相等，即Sshield=Sct。

筆者認為，盾構機下臥土層固結沉降將引起盾構機整體下沉，從而在盾構機頂部與其上部土層之間產生空隙，周圍土層填充該空隙引起地面沉降。計算模型如圖9 所示。

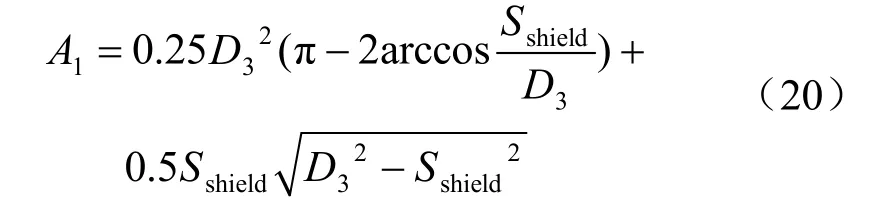
由盾構機位移產生的額外地層損失Vl-a：

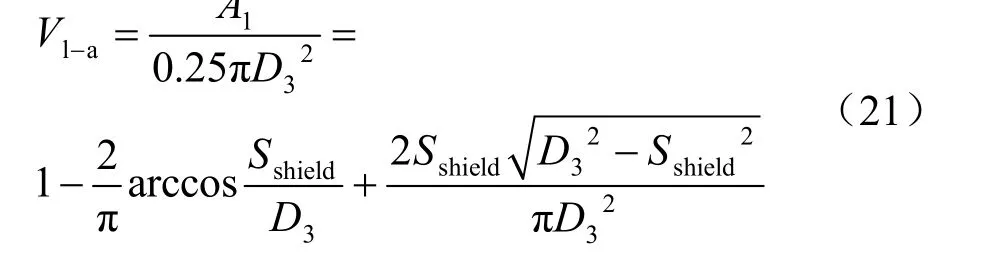
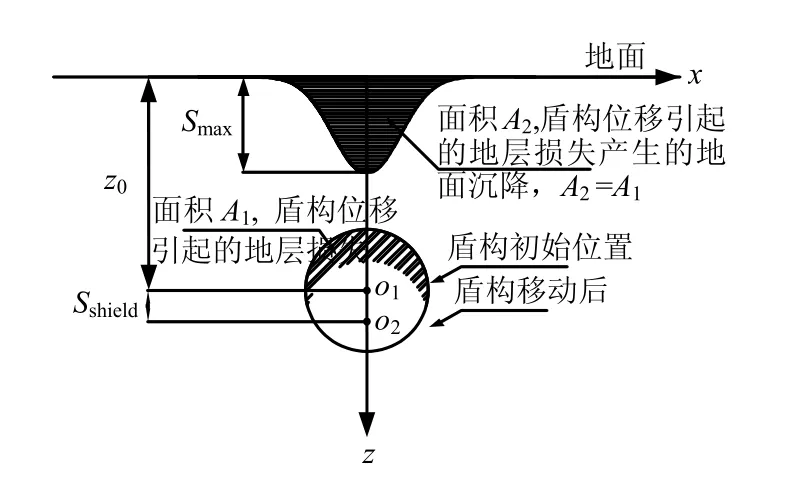
圖9 盾構機位移引起的地面沉降計算模型 Fig.9 Calculation model of ground surface settlements due to the shield’s movement

由地層損失引起的地面沉降，本文應用Peck公式[1,18]計算：

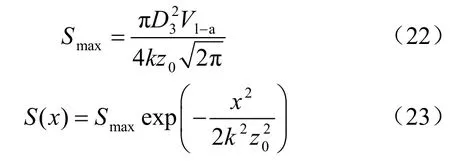
式中：S(x)為地面距離軸線x處地面沉降（mm）；x為距隧道軸線水平距離（m）；Smax為隧道軸線位置地面沉降（mm）；k為沉降槽寬度參數，無量綱。

求得盾構位移Sshield后，代入式（20）～（23），即可求得由于盾構機整體位移引起的地面沉降。

3.3盾構掘進速度及停機時間與地面沉降關系

（1）引入Mindlin解計算盾構下臥土層2σ狀態相對于3σ狀態的附加應力作用下引起的固結沉降，固結時間由盾構掘進速度及停機時間確定；

（2）盾構整體位移與其下臥土層固結沉降相等，聯立式（20）～（23），計算盾構位移引起的地面沉降。

通過以上2步，可以建立盾構掘進速度及停機時間與地面沉降的聯系。

4工程實例分析

4.1工程概況及地質條件

杭州市慶春路過江隧道是浙江省重點建設工程，已于2010年12月28日建成通車。該隧道南北方向垂直穿越錢塘江，盾構段總長為3532.442m，其中東線長為1765.478m，西線長為1766.924m。管片外徑為11.3m，內徑為10.3m，厚為50cm，環寬為2m。管片采用通用契型環，采用6標準塊+2鄰接塊+1封頂塊的分塊形式，錯縫拼裝，縱環向采用高強螺栓連接。

盾構隧道采用2臺泥水平衡盾構機掘進，2臺盾構機均從江南盾構工作井始發，始發段縱向坡度為-4.25%。盾構主機長為10.8m，總重為1170t，外徑為11.65m；盾尾后連接3節拖車，上載砂漿泵、電器液壓設備、主控室等，長約20m，重約2000t。

沿線場地地貌主要為錢塘江河床及兩岸的錢塘江河口沖海積平原，錢塘江南北兩岸已建成標準堤塘，岸區已不受潮汐影響，地貌上屬平原。擬建隧道與錢塘江垂直，該段河面寬度約為1200m，岸區標高為5.0～6.5m（85國家高程），北岸為錢江新城，已建成慶春路，道路兩側以綠化帶為主；南岸以苗木、魚塘為主，因人工魚塘開挖影響，微地貌有一定起伏。

盾構施工主要穿越③層粉砂夾粉土、④層淤泥質粉質黏土、⑤層粉質黏土、⑥層粉質黏土、⑦層粉細砂和⑧層圓礫。各土層物理力學指標見表1。

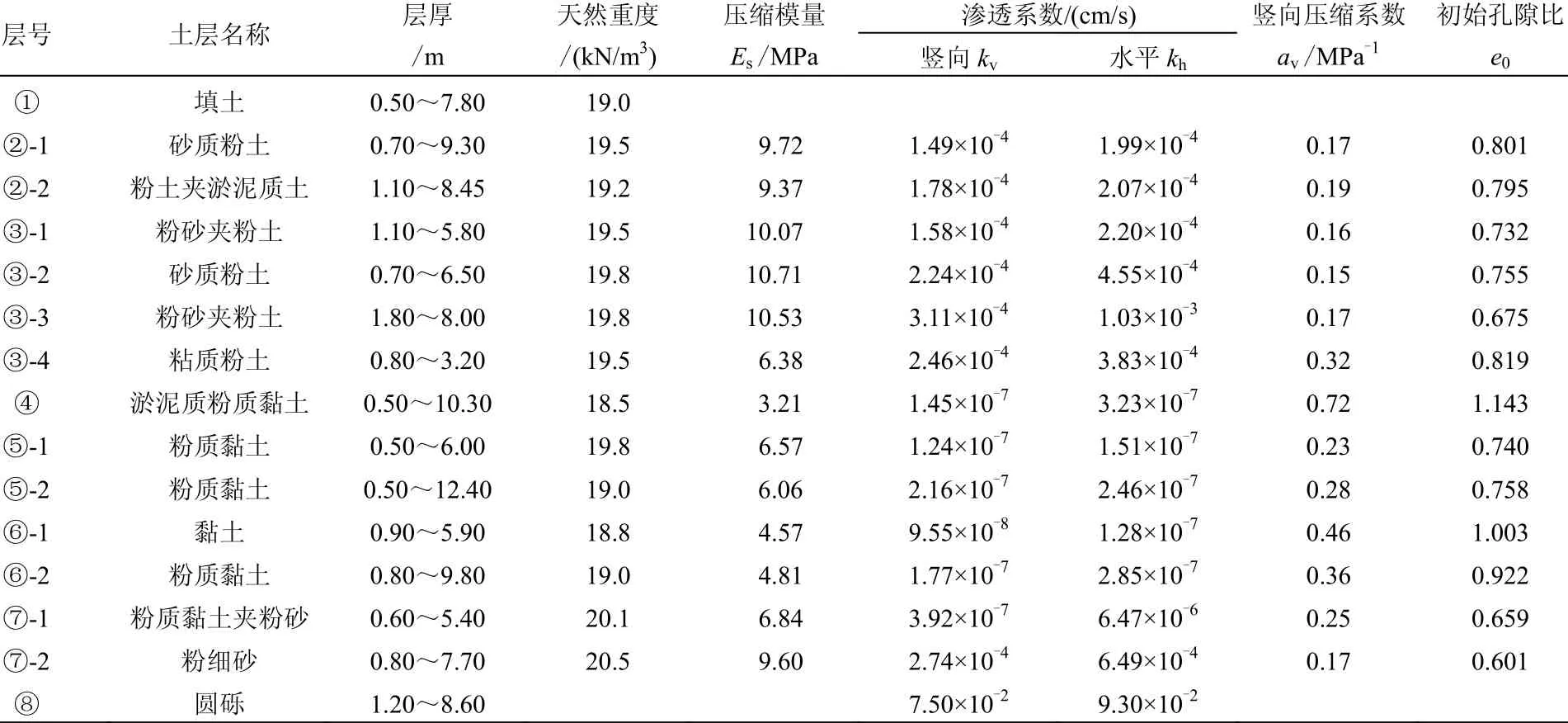
表1場地主要土層物理力學指標Table 1 Soil stratification and physico-mechanical properties

4.2盾構隧道施工引起的地面沉降

東西兩線隧道盾構均從江南工作井出發，穿越錢塘江南岸大堤進入錢塘江底。為控制地面沉降和優化盾構掘進參數控制，在江南工作井和大堤之間地面垂直于隧道軸線方向設置了15個地面沉降監測斷面，編號S1～S15。以示區分，西線監測斷面記為SW，東線記為SE。監測斷面布置如圖10所示。

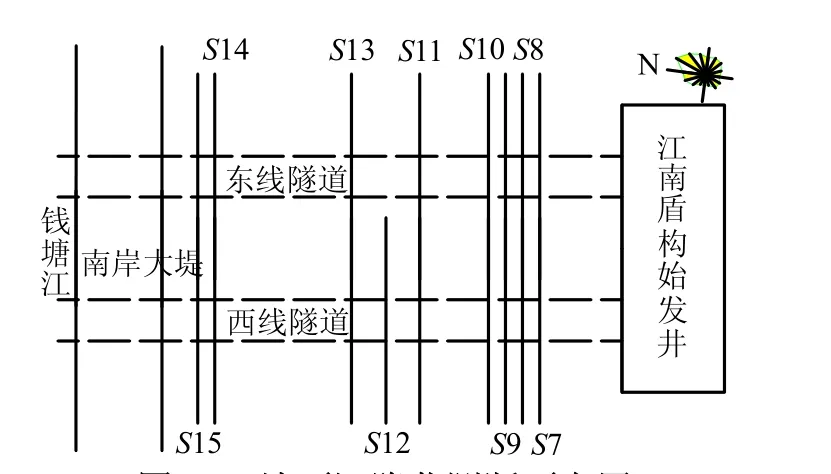
圖10 地面沉降監測斷面布置 Fig.10 Layout of surface settlements monitoring sections

S1～S6 監測斷面處于工作井加固區，地層經加固處理，其沉降已不能反映原狀土體位移受盾構施工的影響，故未加以分析。S7～S15 斷面隧道施工之前為農田，未曾有施工擾動。

圖11 為兩線盾構穿越監測斷面期間掘進進度曲線。圖中虛線自下而上依次代表S7～S15 斷面所處里程。

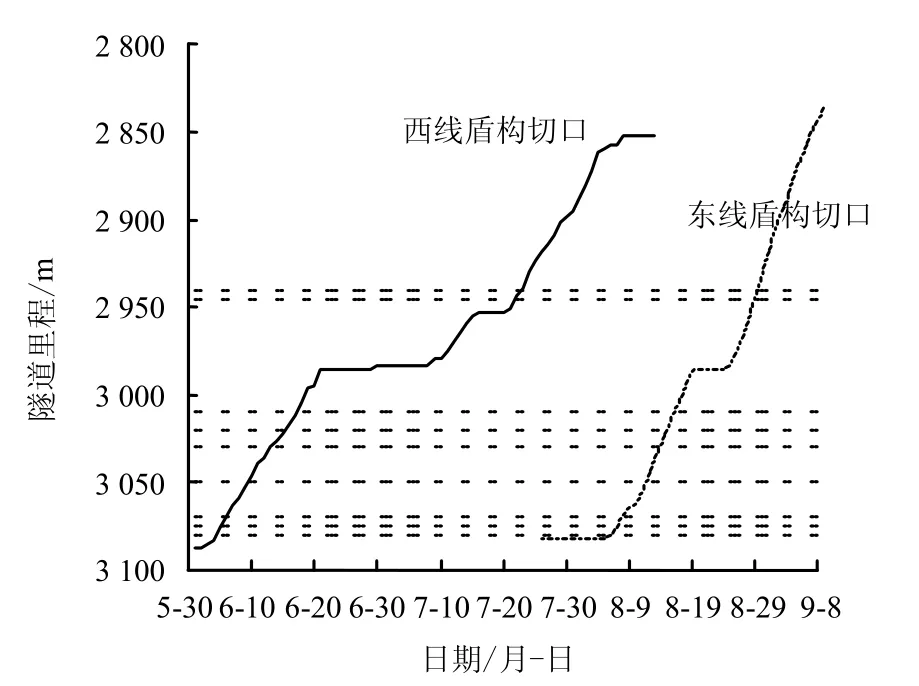
圖11 盾構掘進進度曲線 Fig.11 Advance-time curves of shield machines

由圖11 可見，兩線盾構穿越監測斷面期間掘進速度較均勻，西線盾構非正常停機2 次，東線1 次。若不計停機時間，東西線盾構平均掘進速度分別為8.59 m/d 和5.74 m/d。

圖12 為西線各監測斷面隧道軸線位置地面沉降隨盾尾離開時間的變化曲線。S14、S15 斷面靠近錢塘江南岸大堤堤腳，其地面沉降受大堤影響較大，與之前斷面地面沉降差別較大，未加以分析。t 為盾構盾尾離開監測斷面時間（d），正值表示盾尾已經脫離監測斷面，而負值表示盾尾尚未到達監測斷面；S 為地面位移值，地面隆起記為正值，地面沉降記為負值（mm）。

由圖12 可見，SW7～SW11 沉降規律基本一致：在盾尾脫離約10 d之后，各斷面沉降曲線基本平行，表明各斷面地面沉降速率基本相同，此時地面沉降主要為擾動土體固結引起，可見SW7～SW11 地面固結沉降速率基本一致。

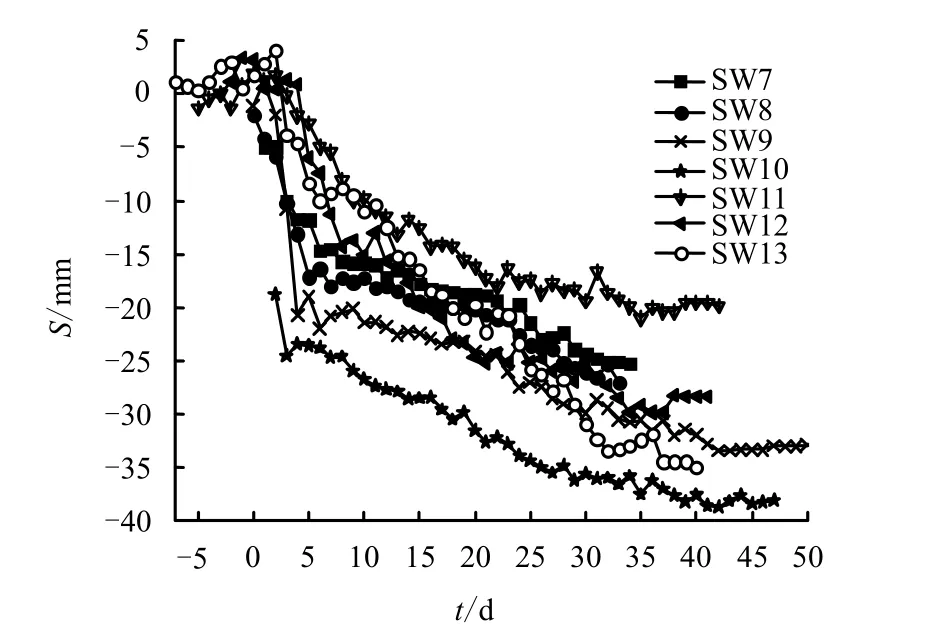
圖12 西線隧道軸線地面沉降隨盾尾離開時間變化曲線 Fig.12 Settlement-time curves of ground surface of west axis

而SW12 和SW13 沉降曲線與SW7～SW11 差別較大：t =10～23 d 期間，SW12 和SW13 沉降曲線基本平行，其斜率明顯大于SW7～SW11 沉降曲線；23 d 之后，SW12 沉降曲線與SW7～SW11 基本平行，而SW13 沉降曲線斜率還是明顯大于其他斷面。

如圖11 所示，西線盾構切口穿越SW12、SW13后停機長達18 d，此時，盾構拖車剛好位于SW13斷面正下方，拖車尾部離開SW12 斷面約2.9 m。

圖13 為東線各監測斷面隧道軸線位置地面沉降隨盾尾離開時間的變化曲線。同樣，S14、S15 斷面未加以分析。

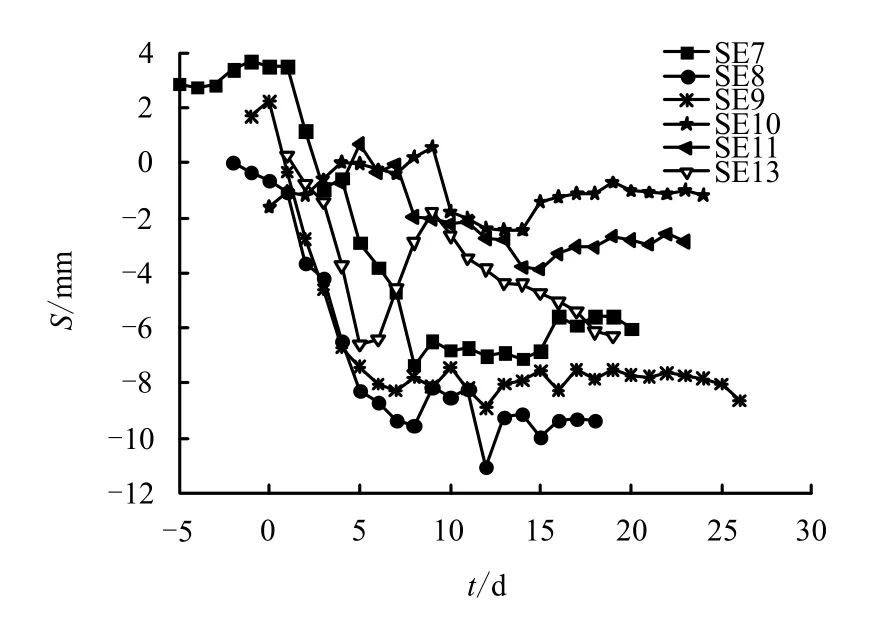
圖13 東線隧道軸線地面沉降隨盾尾離開時間變化曲線 Fig.13 Settlement-time curves of ground surface of east axis

由圖13 可見，盾尾脫離0～9 d 期間，各斷面沉降規律差別較大，主要受盾尾同步注漿控制差異所致；SE7～SE9 在盾尾脫離約8 d 之后地面沉降趨于穩定；SE10、SE11 在盾尾脫離約14 d 之后地面沉降趨于穩定；而SE13 斷面在盾尾脫離約19 d 時，地面仍保持較大的沉降速度。盾尾脫離約9 d 之后，SE13 沉降曲線斜率明顯大于其他斷面，反應了其固結沉降速度遠大于其他斷面。

由圖11 可見，東線盾構切口離開SE13 斷面23.85 m 后，由于設備故障停機7 d，此時盾構拖車剛好位于SE13 正下方。

4.3 理論驗證

由以上分析可見，盾構長時間停機后，所在斷面地面固結沉降速度往往大于其他斷面。現選取SW13 斷面，采用前面所述方法，建立盾構掘進速度及停機時間與地面沉降的聯系。

SW13 剖面如圖14 所示。

圖14 SW13 地質剖面及土中應力計算 Fig.14 Geological profile of monitoring section SW13 and calculation results of soil stresses

4.3.1 土中有效應力計算

計算參數選取：z0=23.26 m，D1=11.3 m，D2= 10.3 m，D3=11.65 m，L =30.8 m，Wshield=34 006 kN（盾構主機與后續拖車重量之和，并考慮到管片運輸行車、拖車長度范圍內拼裝完成管片重量、砂漿運輸行車及施工班組等產生的額外壓重300 t），h = 0.8 m，H = 7.525 m，各土層土體重度見表1，rlining= 25 kN/m3，rgrout=20 kN/m3，rw=9.8 kN/m3，土體泊松比u =0.45，依照施工經驗，取k =0.25。

圖中各個階段應力狀態計算結果見圖14。盾構底部土體有效應力狀態3 及盾構壓重相對于應力狀態3 在土體內部的附加應力詳見圖15。

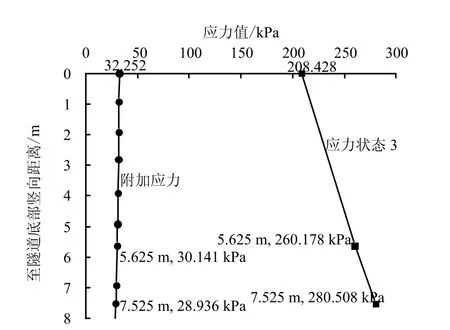
圖15 盾構機底部土體應力狀態3 及附加應力 Fig.15 Stress conditions 3 and additional stress in soils beneath the shield

4.3.2 固結沉降計算

（1）總固結沉降量計算

采用單向壓縮分層總和法[16]計算盾構底部土體固結沉降Sc。圖15 可見，盾構底部土層中附加應力曲線可近似以直線取代，故可取各土層中間位置附加應力值進行計算。

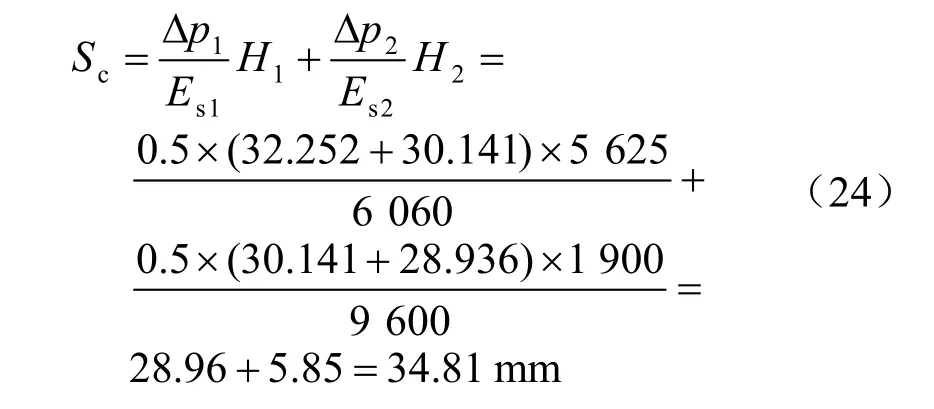
式中：Δp1、Δp2分別為盾構機底部⑤-2 粉質黏土層和⑦-2 粉細砂層中間位置附加應力值（kPa）；Es1、Es2分別為⑤-2 粉質黏土層及⑦-2 粉細砂層壓縮模量，取值見表1（kPa）；H1、H2分別為盾構機底部⑤-2 粉質黏土層及⑦-2 粉細砂層厚度（m）。

由式（24）計算可得，盾構下臥土體，⑤-2 粉質黏土層總固結沉降Sc1=28.96 mm，⑦-2 粉細砂層總固結沉降Sc2=5.85 mm。

（2）平均固結度的計算

國內外眾多工程實例表明，采用太沙基一維固結理論[16－17]計算所得固結沉降速率較實測值明顯要小，這主要因為太沙基一維固結理論僅考慮了孔隙水壓力的豎向消散，而實際問題中水平向的排水加速了超靜水壓力的消散[19－22]。

由表1 可見，本工程盾構穿越各土層水平向滲透系數kh遠大于豎向滲透系數kv，若采用僅考慮豎向滲流的太沙基一維固結理論計算固結度，計算結果將較實際情況偏小。

盾構勻速掘進時，盾構對其下臥土層的附加荷載可簡化為條形均布荷載；而盾構停機時，可簡化為矩形均布荷載，若仍按條形均布荷載計算，結果偏保守；而本文以盾構下方軸線位置的附加應力進行固結沉降計算，最終固結沉降量也偏大。考慮到采用一維固結理論計算固結度結果偏小，可與最終沉降量偏大的計算結果部分抵消，且一維固結理論較二維、三維固結問題簡單，便于工程應用，故本文仍采用太沙基一維固結理論計算盾構下臥土層固結度。

盾構底部有2 層土體，代入式（15）～（19），分別計算各土層的固結沉降，假定單面排水。計算參數取值見表1。計算結果如下：

⑤-2 粉質黏土層

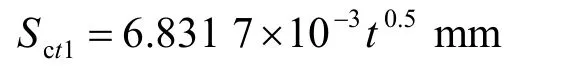
⑦-2 粉細砂層

Ut2=0.99 時，t =2 441.728 s=0.678 3 h 可見，盾構底部⑦-2 粉細砂層孔隙水壓力消散較快，可認為其瞬時完成壓縮沉降，盾構掘進速度快慢及停機時間對該土層沉降不會產生影響。

綜上所述，

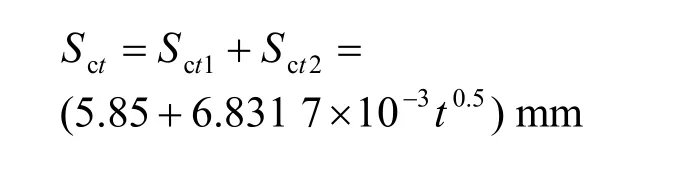
4.3.3 地面沉降計算

應用式（20）～（23）建立盾構下臥土體固結沉降與其引起的地面沉降的關系。計算結果見圖16、17。

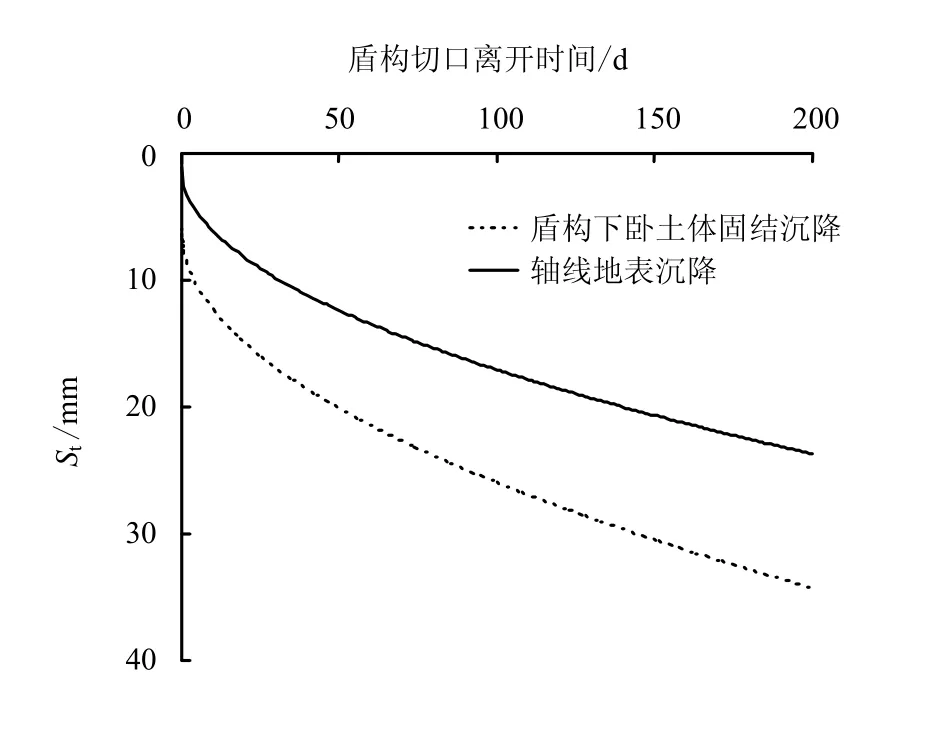
圖16 SW13 斷面盾構底部土體固結沉降及軸線地面沉降 Fig.16 Settlements-time curves of soils beneath the shield machine and ground surface above centerline of the tunnel

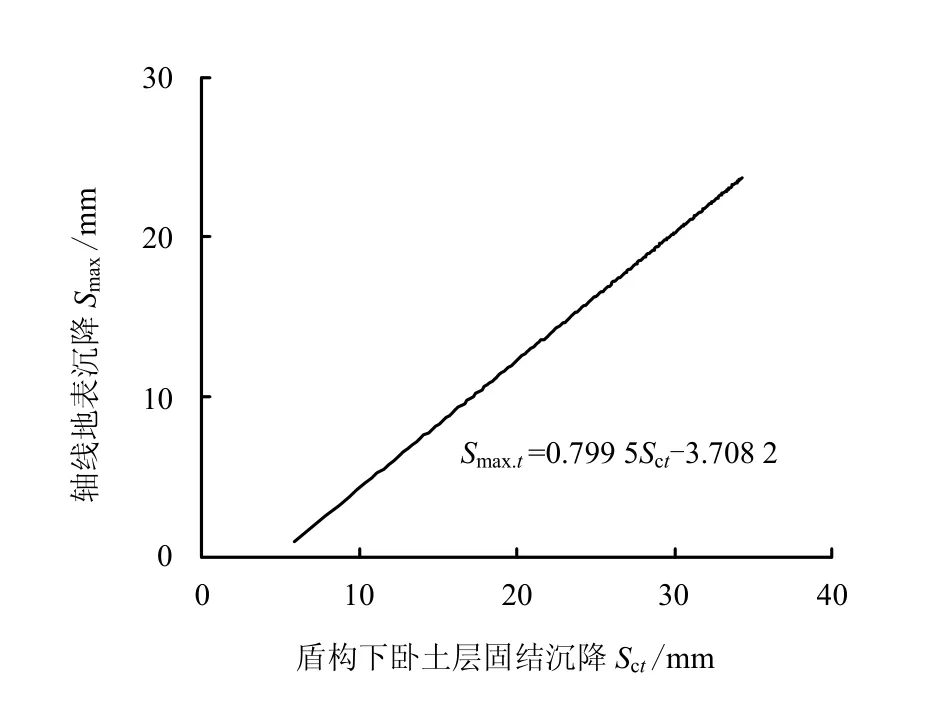
圖17 Smax.t 與Sct 關系曲線 Fig.17 Relation between Smax.t and Sct

由圖17 可見，軸線地面沉降Smax.t和盾構下臥土層沉降Sct近似呈線性關系：

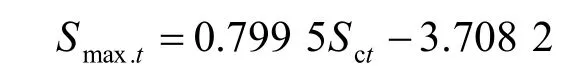
4.3.4 地面沉降比較

（1）西線地面沉降

西線盾構下臥土層受盾構壓重影響時間 2tσ：

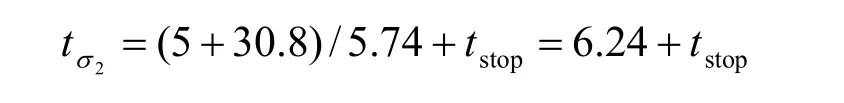
盾構主機長為10.8 m，盾構切口到達某斷面至盾尾離開的時間約為1.88 d，故以盾尾離開監測斷面時間表示，盾構壓重在各監測斷面影響時間為[-1.88 d，4.36 d+tstop]。

盾構盾尾離開SW13 斷面2 d 后，因設備故障停機18 d，之后恢復正常掘進。

SW13 盾構壓縮下臥土層時間為24.24 d，時間段為[-1.88 d，22.36 d]，SW12 斷面盾構壓縮下臥土層時間段為[-1.88 d，22.36 d]，其他斷面盾構壓縮下臥土層時間段為[-1.88 d，4.36 d]。

t =[-1.88 d，4.36 d]，各監測斷面盾構下臥土層均受到盾構產生的附加應力的影響，隨后[4.36 d，22.36 d]期間，僅SW12、SW13 還受其影響。

由于各監測斷面地質剖面及隧道埋深不盡相同，因此，盾構下臥土層固結沉降及固結沉降與地面沉降的關系不盡相同。考慮到各監測斷面相離較近，土層及隧道埋深情況基本一致，近似用圖16曲線計算其他斷面盾構壓縮下臥土層固結沉降及引起的地面沉降。

圖18 為各斷面沉降比較。圖中，Sstop為計算所得由盾構停機引起的地面沉降，SW12-Sstop、SW13-Sstop分別為SW12 和SW13 地面實測沉降與由盾構停機引起的地面沉降之差。

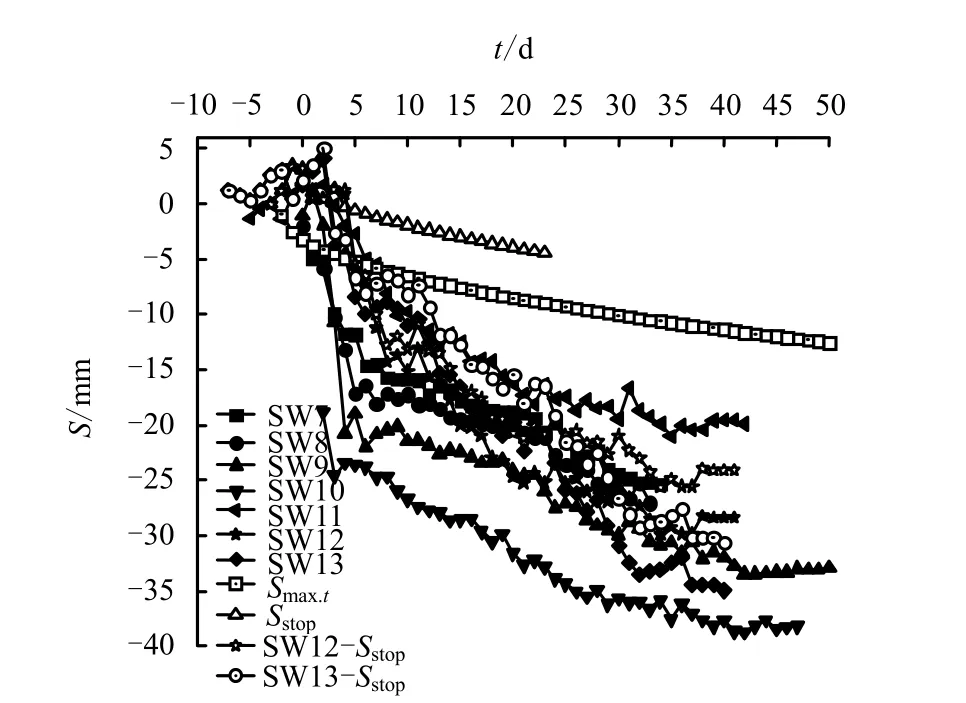
圖18 西線各斷面沉降情況 Fig.18 Ground settlements of monitoring sections for west route

由圖18 可見，去除盾構停機引起的地面沉降之后，SW12 斷面沉降與其他斷面沉降規律基本相同。而SW13 斷面，去除盾構停機引起的地面沉降之后，在停機時間段內（t=[4.36 d，22.36 d]）的地面沉降規律與其他斷面基本一致，而隨后監測時間內的地面沉降速度還是較其他斷面要大。

造成以上差別的原因，筆者認為，由于盾構機停機時產生較大沉降，再次掘進時姿態較難控制，由于拖車尾部已經離開SW12 斷面約2.9 m，掘進不會對SW12 產生顯著擾動；而SW13 斷面剛好位于拖車中部，對其擾動較大，這是圖18 所示SW13斷面地面沉降雖已不受盾構壓重影響但仍保持較大沉降速度的原因。

（2）東線地面沉降

東線盾構下臥土層受盾構壓重影響時間 1tσ：

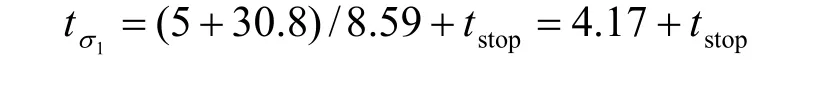
盾構機切口到達某斷面至盾尾離開的時間約為1.26 d，故以盾尾離開監測斷面時間表示，盾構壓重在各監測斷面影響時間為[-1.26 d，2.91 d+tstop]。

盾尾離開SE13 斷面約13.05 m 后（拖車剛好位于SE13 正下方），因設備故障停機7 d，之后恢復正常掘進。

SE13 斷面盾構壓縮下臥土層時間為11.17 d，時間段為[-1.26 d，9.91 d]，其他斷面盾構壓縮下臥土層時間段為[-1.26 d，2.91 d]。

SE13 斷面地質情況及隧道埋深與SW13 基本一致，因此，可近似使用圖16 結果。對于其他斷面，盾構壓縮下臥土層引起的地面沉降仍近似用圖16曲線表示。

圖19 為各斷面沉降比較。

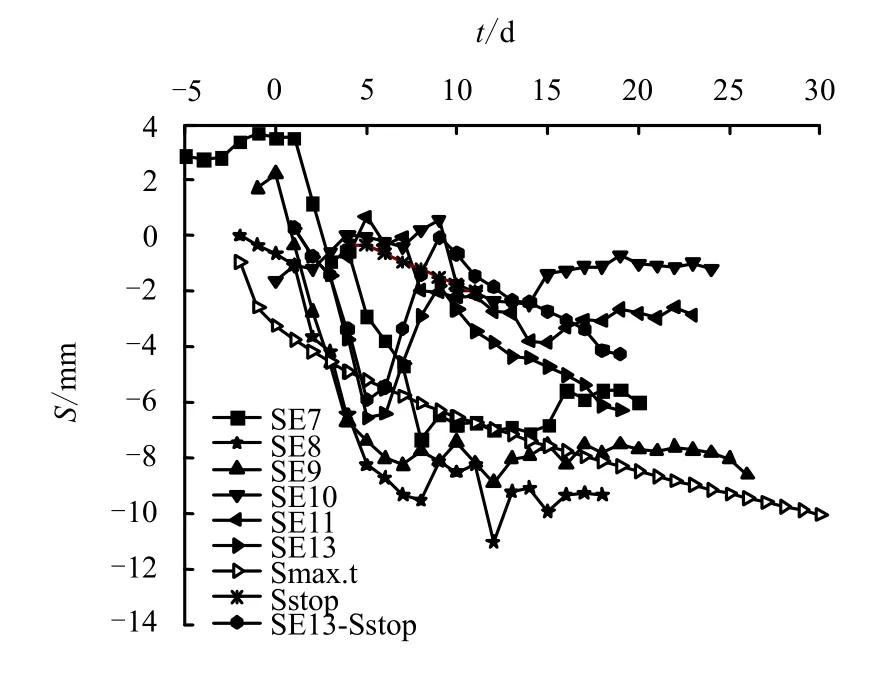
圖19 東線各斷面沉降情況 Fig.19 Ground settlements of monitoring sections for east route

由圖可見，扣除時間段[2.91 d，9.91 d]內由盾構停機引起的地面沉降之后，在該時間段內SE13斷面沉降規律與其他斷面仍不一致。究其原因，主要為該段時間盾尾注漿差異引起的。SE8 和SE9 斷面該時間段內地面持續沉降，而SE10、SE11 斷面則發生隆起，SE13 斷面先是持續沉降后又較大隆起。由于盾尾注漿壓力作用差異，各個監測斷面總沉降在時間段[0，10 d]差異較大，所以SE13 扣除盾構停機引起的地面沉降后，其沉降規律在該時間段內與其他斷面仍不同。

盾尾脫離10 d 之后，SE13 已不受盾構附加荷載影響，但其地面沉降速度仍較其他斷面要大，而其他斷面較一致。該差別主要為盾構恢復掘進時對SE13 斷面的施工擾動所致。

（3）兩線地面沉降

綜上可見，西線盾構各監測斷面地面沉降受盾尾同步注漿引起的差異較小，總沉降規律基本相同，扣除盾構停機影響后，本文所述理論較好地解釋了盾構停機期間地面沉降較大的原因，盾構下臥土層固結沉降及其引起的地面沉降計算理論基本正確。

東線盾構各監測斷面地面沉降受盾尾同步注漿引起的差異較大，總沉降規律在盾尾剛脫離初期(0～10 d)差別較大，所以扣除盾構停機影響后，各斷面沉降規律仍難一致。

兩線隧道地面沉降可以看出，盾構長時間在某一斷面擱置時，由于壓縮下臥土層引起盾構整體下沉，在恢復掘進時，盾構姿態較難控制，會引起較大施工擾動，加劇地面沉降。

5 結 論

（1）引入Mindlin 解計算盾構壓重在其下臥土層產生的附加應力，采用單向分層總和法計算下臥土層總固結沉降，使用太沙基一維固結理論計算盾構壓重影響時間內的沉降量，并用Peck 公式建立起該固結沉降與地面沉降的聯系。杭州慶春路越江隧道地面沉降的實測數據驗證表明，上述理論基本可以建立盾構掘進速度與停機時間和盾構壓縮下臥土層引起的地面沉降的聯系。

（2）當盾構下臥土層為黏性土，黏土層下臥砂土或圓礫等透水層時，盾構壓重引起的地面沉降較大。盾構下臥土層的固結沉降和其引起的地面沉降基本呈線性。

（3）盾構附加荷載在其下臥土層的作用時間取決于盾構掘進速度和停機時間；掘進速度越快，正常停機或非正常停機時間越短，盾構附加應力作用下其下臥土層固結沉降越小，進而其引起的地面沉降越小。因此，在其他掘進參數控制一致的前提下，提高掘進速度，避免非正常停機或降低停機時間，有利于減少盾構施工引起的地面沉降。

（4）盾構長時間停機后整體下沉，恢復掘進時，姿態較難控制，會加大地層擾動，加劇地面沉降。

本文在建立計算模型時，應用了許多假定，附加應力、固結沉降及固結度的計算受計算公式和土體參數選取的影響較大，且計算結果僅在本工程中得到驗證。因此，對于本文理論的普遍適用性有待在更多的工程實踐中加以驗證和改進。

[1] PECK R B. Deep excavations and tunneling in soft ground[C]//Proceedings of 7th International Conference on Soil Mechanics and Foundation Engineering. Mexico City: Thomas Telford, 1969: 225－290.

[2] YOSHIKOSHI WATARU, WATANABE OSAMU, TAKAGI NOBUO. Prediction of ground settlements associated with shield tunnelling[J]. Soils and Foundations, 1978, 18(4): 47－59.

[3] 朱才輝, 李寧, 柳厚祥, 等. 盾構施工工藝誘發地表沉降規律淺析[J]. 巖土力學, 2011, 32(1): 158－164. ZHU Cai-hui, LI Ning, LIU Hou-xiang, et al. Analysis of ground settlement induced by workmanship of shield tunnelling[J]. Rock and Soil Mechanics, 2011, 32(1): 158－164.

[4] LEE K M, ROWE R KERRY, LO K Y. Subsidence owing to tunneling. I. Estimating the gap parameter[J]. Canadian Geotechnical Journal, 1992, 29: 929－940.

[5] ROWE R KERRY, LEE K M. Subsidence owing to tunneling. II. Evaluation of a prediction technique[J]. Canadian Geotechnical Journal, 1992, 29: 941－954.

[6] ROWE R KERRY, LEE K M. Subsidence owing to tunneling. II. Evaluation of a prediction technique:1Reply[J]. Canadian Geotechnical Journal, 1994, 31: 467－469.

[7] PARK K H. Elastic solution for tunnelling-induced ground movements in clays[J]. International Journal of Gemechanics, 2004, 4(4): 310－318.

[8] WEI-I CHOU, ANTONIO BOBET. Predictions of ground deformations in shallow tunnels in clay[J]. Tunnelling and Underground Space Technology, 2002, 17(1): 3－19.

[9] NOMOTO TOSHI, IMAMURA SHINICHIRO, HAGIWARA TOSHIYUKI, et al. Shield tunnel construction centrifuge[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(4): 289－300.

[10] FINNO RICHARD J, CLOUGH G WAYNE. Evaluation of soil response to EPB shield tunneling[J]. Journal of Geotechnical Engineering, 1985, 111(2): 155－173.

[11] CLOUGH G WAYNE, SWEENEY BRYAN P, FINNO RICHARD J. Measured soil response to EPB shield tunneling[J]. Journal of Geotechnical Engineering, 1983, 109(2): 131－149.

[12] VERRUIJT A, STRACK O E. Buoyancy of tunnels in soft soils[J]. Géotechnique, 2008, 58(6): 513－515.

[13] MINDLIN R D. Force at a point in the interior of a semi-infinite solid[J]. Journal of Applied Physics, 1936, 7(5): 195－202.

[14] SKOPEK J. The influence of foundation depth on stress distribution[C]//Proceedings of the 5th International Conference on Soil Mechanics and Foundation Engineering. Paris: [s. n.], 1961.

[15] POULOS H G, DAVIS E H. Elastic solutions for soil and rock mechanics[M]. New York, London, Sydney, Toronto: John Wiley & Sons, inc., 1974.

[16] 龔曉南. 土力學[M]. 北京: 中國建筑工業出版社, 2002: 99－114.

[17] 龔曉南. 高等土力學[M]. 杭州: 浙江大學出版社, 1996: 92－111.

[18] O’REILLY M P, NEW B M. Settlements above tunnels in the United Kingdom-their magnitude and prediction[C]// Tunneling 82. Papers Presented at the third International Symposium. London: Institution of Mining and Metallurgy, 1982: 173－182.

[19] 李廣信. 高等土力學[M]. 北京: 清華大學出版社, 2004.

[20] 顧曉魯, 錢鴻縉, 劉惠珊, 等. 地基與基礎(第三版)[M]. 北京: 中國建筑工業出版社, 2003: 138－198.

[21] CRAWFORD C B. State of the art: evaluation and interpretation of soil consolidation tests[R]// Consolidation of Soils: Testing and Evaluation. Lauderdale: the ASTM Symposium on Consolidation Behavior of Soils, Ft., 1985: 71－101.

[22] DAVIS E H, POULOS H G. The use of elastic theory for settlement prediction under three-dimensional conditions[J]. Géotechnique, 1968, 18(1): 67－91.