嚴(yán)寒地區(qū)鐵路路基凍融沉降數(shù)值模擬研究

趙 歡,李東升

(1.陜西鐵路工程職業(yè)技術(shù)學(xué)院,陜西渭南 714000； 2.石家莊鐵道大學(xué)土木工程學(xué)院, 石家莊 050043)

1 概況

某鐵路客運(yùn)專線地處我國嚴(yán)寒地區(qū)，年平均氣溫-12.4～10.9 ℃，極端最高溫度39.8 ℃，極端最低氣溫達(dá)-40 ℃，最大積雪厚度30 cm，最大季節(jié)凍土深度達(dá)205 cm，冬季寒冷而漫長，每年從10月底開始凍結(jié)，翌年5～6月全部融化，沿線穿越軟土、季節(jié)性凍土等地區(qū)，地質(zhì)情況復(fù)雜。在高速車輛沖擊荷載以及季節(jié)性凍土熱融沉降和凍脹變形的長期作用下，路基的沉降變形是不可避免的，故建立路基凍融循環(huán)和列車動荷載耦合作用下的路基沉降模型，對路基沉降進(jìn)行長期預(yù)測，具有重要的工程意義。

2 模型的建立

本文在線路上選取DK503+580路基典型斷面進(jìn)行數(shù)值模擬研究，模型建立如下。

(1)斷面情況，見表1。

(2)軌道板，0.3 m厚；路基填筑材料層：①上層級配碎石和中粗砂，0.6 m厚；②下層非凍脹土和A、B組填料2.4 m厚。為了方便計算，這里把路基填筑部分的材料簡化為填土3 m一層材料。

(3)地基土可分為2層：①上層為粉黏土，厚度在3 m左右；②下層為砂土，厚度大于20 m。

表1 某客運(yùn)專線DK503+580路基斷面情況

(4)可影響范圍：縱向從天然地表向下延伸20 m，橫向從路堤邊界向左右各延伸10 m。

(5)網(wǎng)格劃分：沿鐵路縱向取50 m做為分析單元，50 m內(nèi)共分成20份網(wǎng)格。

建立的模型見圖1。

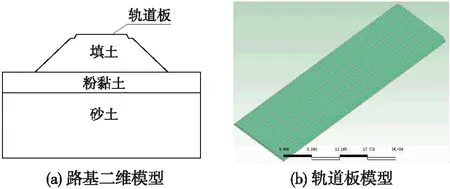
圖1 路基模型

3 介質(zhì)參數(shù)的選取

根據(jù)工程實(shí)況，可以把一個凍融循環(huán)下的路基凍融狀態(tài)劃分為如下幾個階段：

(1)凍結(jié)時間設(shè)定為11月15日至12月15日，該過程按變溫凍結(jié)過程計算，溫度變化范圍-5～6 ℃；

(2)從12月15日至次年3月15日，該過程按恒溫-4℃凍結(jié)過程計算；

(3)從次年3月15日至次年4月15日，該過程按變溫融化過程計算，溫度變化范圍-4～12 ℃；

(4)從次年4月15日至次年5月15日，該過程按恒溫12℃融化過程計算；

(5)從次年5月15日至次年11月15日，認(rèn)為土體處于未凍結(jié)狀態(tài)。

實(shí)際上路基土體的物理力學(xué)性質(zhì)隨溫度的變化而變化，這里為了計算方便，作如下假設(shè)。

(1)在一個凍融循環(huán)內(nèi)，每個階段內(nèi)的路基土體物理力學(xué)性質(zhì)是不變的，即變溫凍結(jié)、恒溫凍結(jié)、變溫融化、恒溫融化和未凍結(jié)5個階段各對應(yīng)不同的土體物理力學(xué)性質(zhì)不變，這是基于每個階段溫度的變化不是太大，故對土體力學(xué)性質(zhì)的影響不太明顯的基礎(chǔ)上作出的假設(shè)。

(2)根據(jù)實(shí)際工程路基地溫的監(jiān)測數(shù)據(jù)[3]，在地基土體中，由于監(jiān)測數(shù)據(jù)表明凍深不超過3 m，故受凍融影響的主要是地基粉黏土部分，從而可以認(rèn)為砂土的材料參數(shù)在模擬過程中保持恒定，見表2。

(3)路堤部分簡化為一種材料即填土。填土和地基粉黏土都受凍融的影響，根據(jù)前面對一個凍融循階段的劃分可知，兩種土體在每個凍融循環(huán)過程中都要經(jīng)歷5個階段，這5個階段分別為：變溫凍結(jié)、溫恒凍結(jié)、變溫融化、恒溫融化和未凍結(jié)。在不同的階段土體的力學(xué)參數(shù)是不一樣的，故每一個凍融循環(huán)下土體力學(xué)參數(shù)也是不一樣的，從而地基土體的力學(xué)參數(shù)要依據(jù)每個階段每個凍融循環(huán)來確定，具體過程如下。

表2 砂土的力學(xué)參數(shù)

①首先確定初始凍融循環(huán)每個階段的材料力學(xué)參數(shù)。根據(jù)相關(guān)試驗(yàn)數(shù)據(jù)[1]，初始凍融循環(huán)的不同階段填土和粉黏土的力學(xué)參數(shù)見表3和表4。

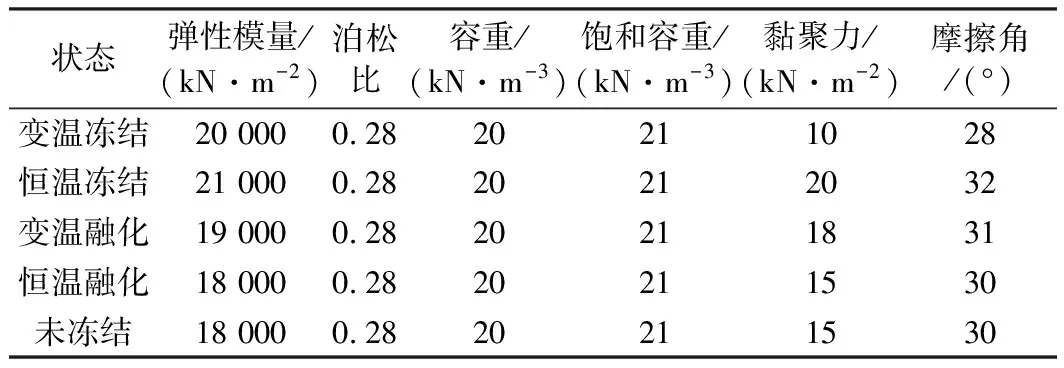
表3 初始凍融循環(huán)填土的力學(xué)參數(shù)特征值

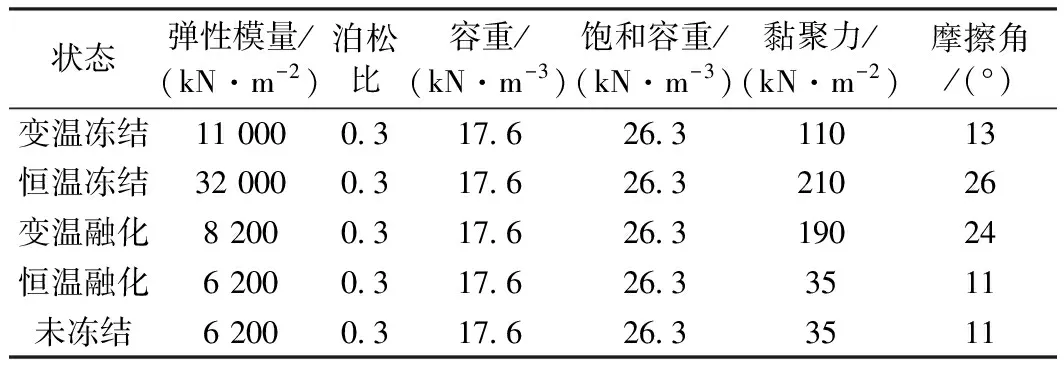
表4 初始凍融循環(huán)粉黏土的力學(xué)參數(shù)特征值

②在數(shù)值計算過程所輸入的參數(shù)按照凍融循環(huán)中每個階段來確定，即以第1個階段(變溫凍結(jié))的數(shù)值計算結(jié)果作為第2個階段計算的材料特征值，依次類推就能得出填土和粉黏土在各個凍融期間的材料特征值。

在模型定義的約束條件下有

(1)

式中σi——第i階段的初始軸向應(yīng)力值；

εi——第i階段地基土初始軸向應(yīng)變；

λi、ζ——受圍壓、含水量影響參數(shù)，分別取1.4和0.3；

A1、B1——含水量影響參數(shù)，分別取1.85和1.97。

如果不考慮蒸發(fā)因素，則土體中含水量在路基的沉降過程中不發(fā)生變化，故式(1)中的參數(shù)ζ，A1，B1在模擬中取定值，但λi是變化的，因?yàn)閲鷫翰还潭ǎ实趇+1階段的λi+1可由式(2)變形得到

(2)

式中，σi+1為第i+1階段初始軸向應(yīng)力；εi+1為第i+1階段初始軸向應(yīng)變。它們分別為第i階段末的應(yīng)力應(yīng)變值，從數(shù)值模擬中得出。

各種材料特征值確定的具體過程如下。

①泊松比、容重和飽和容重在凍融循環(huán)中取定值，分別為0.3、17.6 kN/m和26.3 kN/m；

②變形模量的確定：根據(jù)式(1)和式(2)得出每個階段的初始應(yīng)力、應(yīng)變值，然后利用公式E=σ/ε就可以計算出變形模量。

③內(nèi)摩擦角和黏聚力的確定：在式(1)中，將σ看作主應(yīng)力差，在每個階段中選取3個應(yīng)變值，其中2個應(yīng)變值分別為該階段的初始應(yīng)變和結(jié)束應(yīng)變，另外一個應(yīng)變值處于兩者之間的任意一個值，把3個應(yīng)變值代入到式(1)中就可以計算出相對應(yīng)的主應(yīng)力差，有了3個主應(yīng)力差值就可以繪制出摩爾庫侖圓，通過摩爾庫侖圓的包絡(luò)線就能得到該階段土體的內(nèi)摩擦角和黏聚力。

因?yàn)镸idas軟件只接受離散點(diǎn)的材料特征參數(shù)，對函數(shù)形式的材料特征值尚無相應(yīng)的輸入程序，故本次模擬中對參數(shù)特征值按階段逐步進(jìn)行輸入。

4 沉降量的計算分析

4.1 列車動荷載下的豎向位移

根據(jù)文獻(xiàn)[2]，高速鐵路動荷載可按下式計算

Pd=Ps(1+0.003ν)(3)

式中Ps——活載，取為1 100 kN；

ν——列車速度，取線路設(shè)計速度350 km/h。

所以高速鐵路動載為

Pd=1 100×(1+0.003×350)=2 255 kN(4)

假定動荷載在基礎(chǔ)板上均勻分布，路基板寬度3.5 m，荷載縱向作用深度為10 m，擴(kuò)散系數(shù)取0.96，則作用在路基面上的動應(yīng)力為

qd=0.96×2 255/35=61.6 kPa(5)

故列車動荷載值取為61.8 kPa，根據(jù)Y225K型旅客列車的各軸間距(同節(jié)列車軸間距18 m，相鄰兩節(jié)列車軸間距7.5 m)，列車運(yùn)行速度按設(shè)計值350 km/h計算，得到列車平均軸頻率為28 Hz。

根據(jù)文獻(xiàn)[2]，振動波型模型見公式

σd=40[1-cos(2π×20)t](6)

根據(jù)上述的材料參數(shù)、荷載輸入以及阻尼，利用Midas計算出列車經(jīng)過一次對應(yīng)的Z方向(豎向)位移，分析結(jié)果見圖2～圖7。

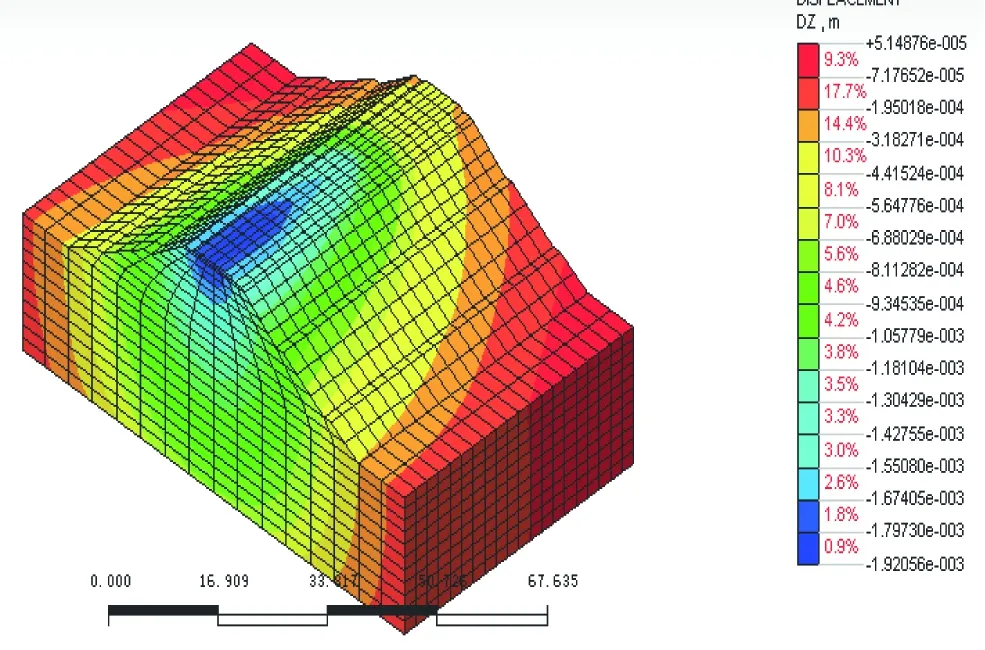
圖2 列車進(jìn)入0.7 s時的Z方向位移

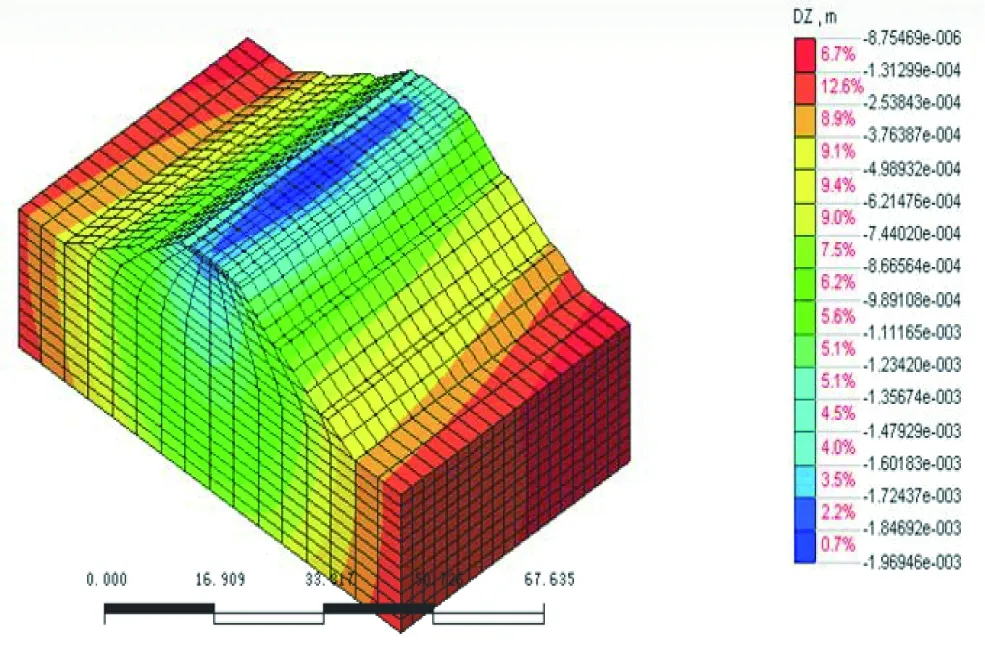
圖3 列車進(jìn)入1.0 s時的Z方向位移

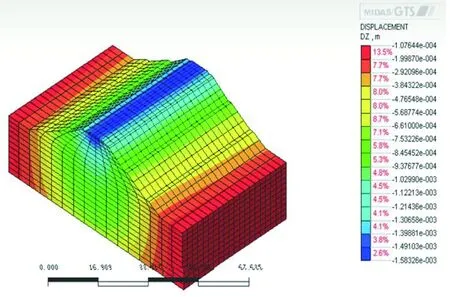
圖4 列車進(jìn)入1.7 s時的Z方向位移

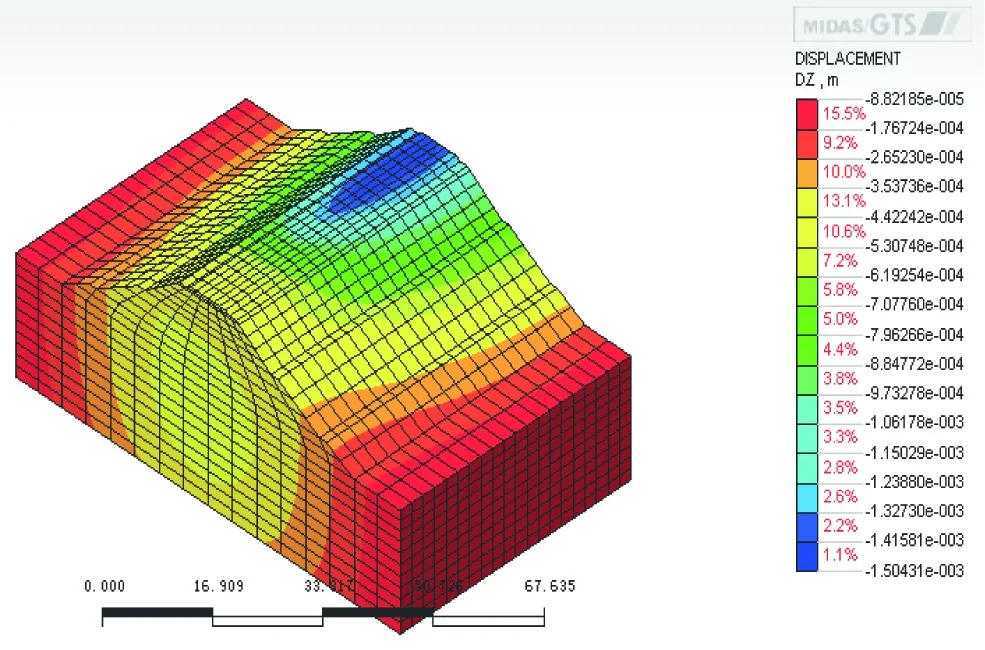
圖5 列車進(jìn)入2.4 s時的Z方向位移

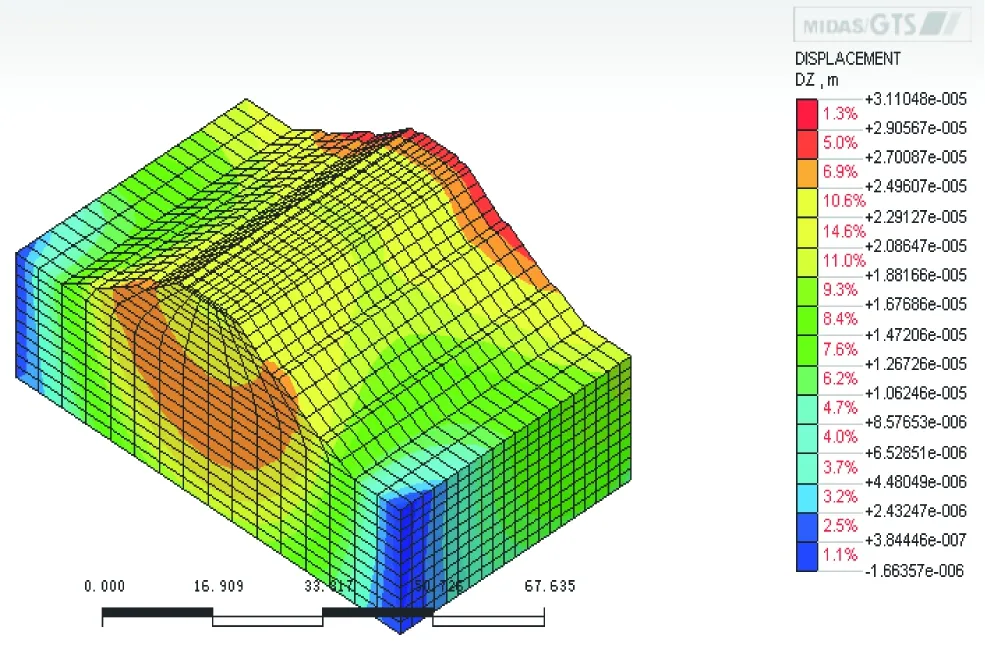
圖6 列車進(jìn)入3.5 s時的Z方向位移

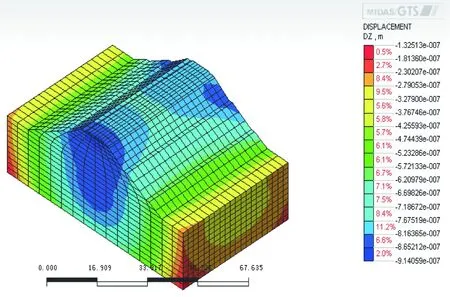
圖7 列車進(jìn)入5.0 s時的Z方向位移

4.2 沉降量計算

根據(jù)計算模型設(shè)定長度(50 m)及Y225K型旅客列車軸間距(同節(jié)列車軸間距18 m，相鄰兩節(jié)列車軸間距7.5 m，共25.5 m)可以將上述計算結(jié)果看作是由2次振動產(chǎn)生，據(jù)此，按如下步驟計算動載與凍融循環(huán)耦合下地基沉降量。

(1)將一個凍融循環(huán)過程按變溫凍結(jié)、恒溫凍結(jié)、變溫融化、恒溫融化和未凍結(jié)劃分為5個階段，根據(jù)前面溫度變化時間設(shè)定，各階段對應(yīng)的時間為：

①變溫凍結(jié)階段歷時30 d；

②恒溫凍結(jié)階段歷時90 d；

③變溫融化階段歷時30 d；

④恒溫融化階段歷時30 d；

⑤未凍結(jié)階段歷時為185 d。

假設(shè)每天通車10次，結(jié)合列車的軸頻率28 Hz，則可以確定振次為280次/d，每個階段中以10 d為一個計算周期，則每個計算周期的振次為2 800次。根據(jù)實(shí)驗(yàn)室里動三軸試驗(yàn)結(jié)果可以知道[5]：當(dāng)圍壓較大時，可以認(rèn)為軸向應(yīng)變值與振動次數(shù)成正比。故每個計算周期中的累積沉降量為該周期中第一次振動所產(chǎn)生的殘余位移值與周期內(nèi)振動次數(shù)的乘積。

(2)根據(jù)第i個計算階段的累積沉降量來計算第i+1個計算階段的材料力學(xué)參數(shù)特征值。本文具體列出模擬5次凍融循環(huán)，其相對應(yīng)的具體材料力學(xué)參數(shù)特征值見表5、表6。

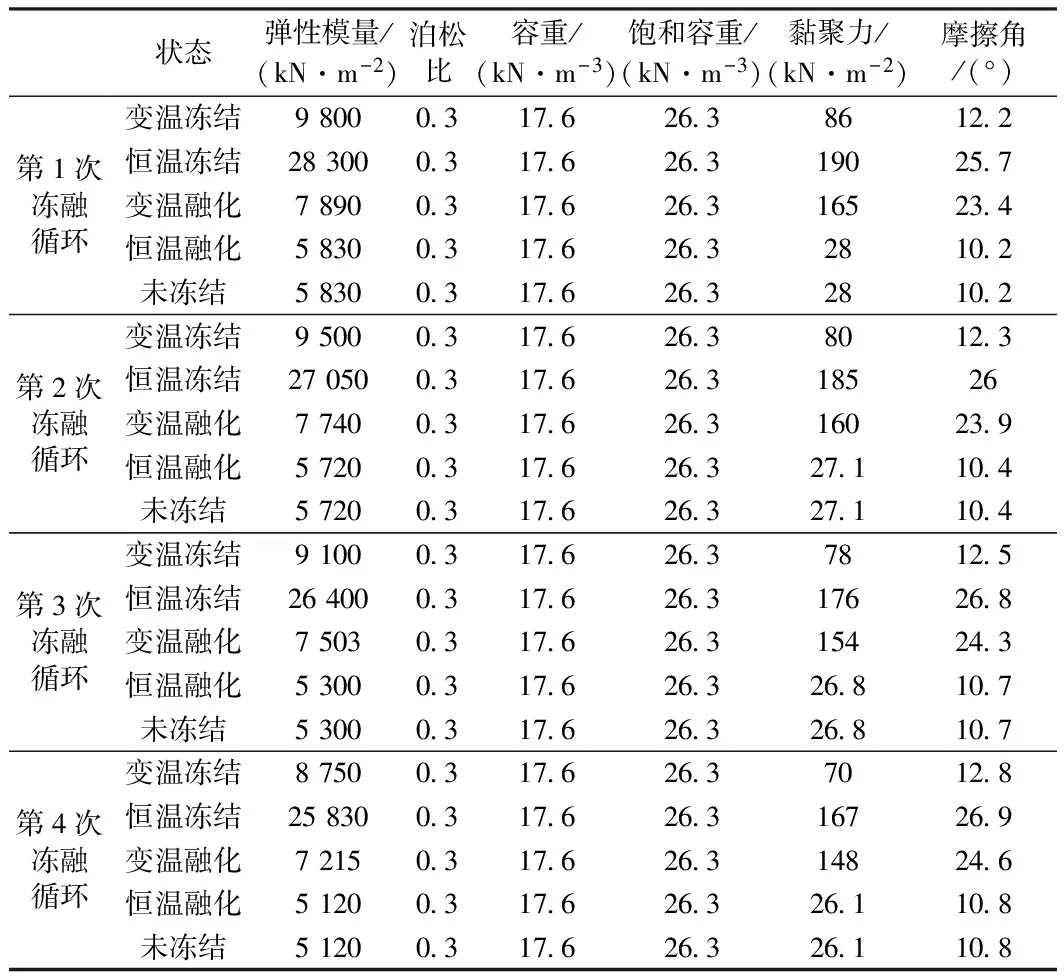
表5 粉黏土的力學(xué)參數(shù)特征值

從上面的材料力學(xué)參數(shù)可以看出，路堤填土的防凍性能較好，凍結(jié)期和融化期內(nèi)的力學(xué)性質(zhì)變化很小；地基粉黏土容易受凍融作用的影響，凍結(jié)狀態(tài)和融化狀態(tài)的力學(xué)性質(zhì)相差很大，須采取一定的地基加固措施。在凍融循環(huán)的影響下，可以發(fā)現(xiàn)材料的變形模量和黏聚力是減小的，但摩擦角是增大的。

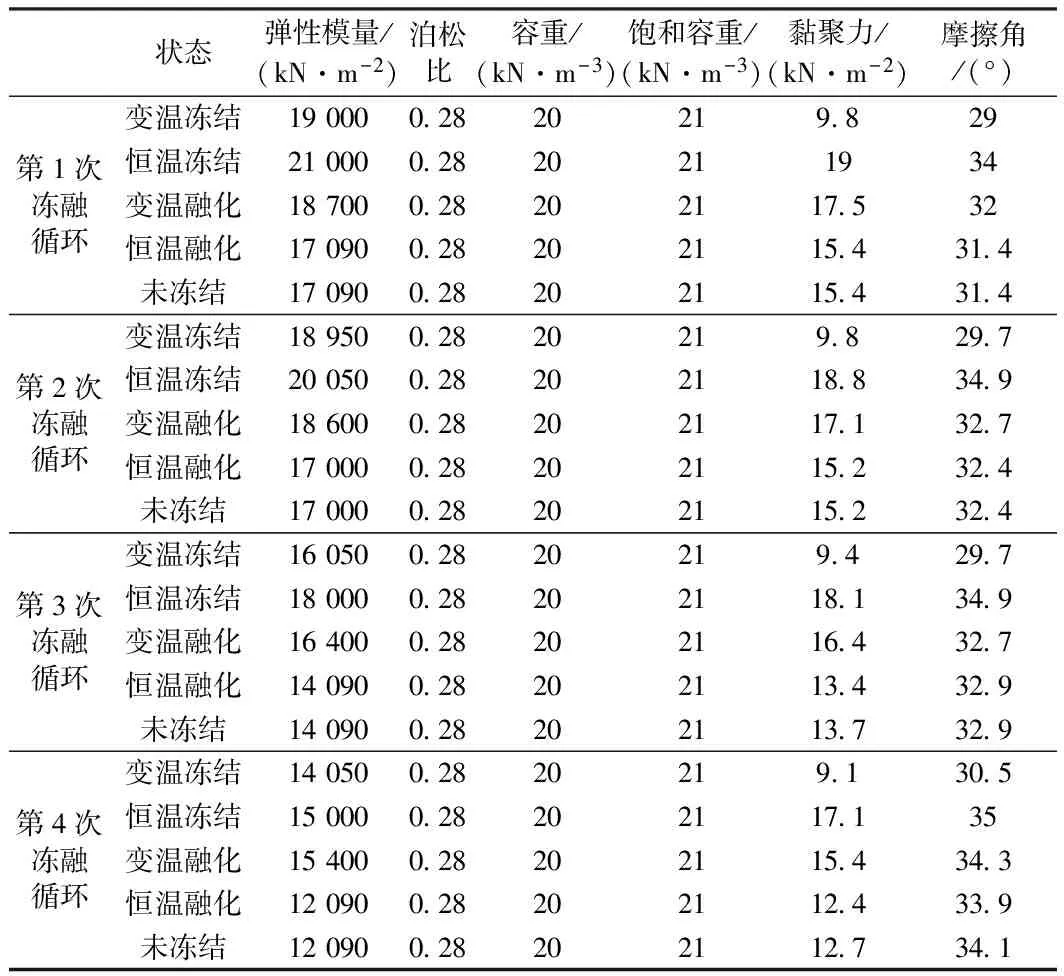
表6 填土的力學(xué)參數(shù)特征值

(3)根據(jù)確定的材料力學(xué)參數(shù)特征值，利用Midas計算第i+1計算周期中第1次振動所產(chǎn)生的沉降量。然后利用其殘余沉降值乘以這個周期的振次，就得到了這個周期的沉降量，進(jìn)而可以得到該階段沉降量和這個凍融循環(huán)的沉降量。

(4)重復(fù)(2)～(3)步可計算出多次凍融循環(huán)下高速鐵路地基的沉降量。

根據(jù)上述計算步驟，10次凍融循環(huán)作用下路基累積沉降值的計算結(jié)果如圖8所示。

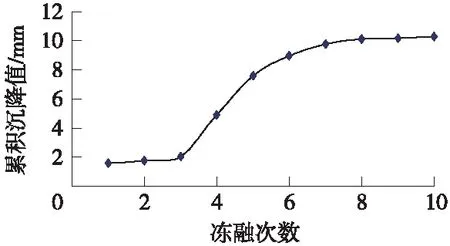
圖8 10次凍融循環(huán)作用下路基累積沉降曲線

從模擬計算結(jié)果中可以看出，在前3個凍融循環(huán)過程中，路基沉降量增長緩慢，累積沉降值為2.08 mm，這說明所選用的材料已經(jīng)消除了凍融所造成的豎向位移，其增長的數(shù)值源于粉黏土在動荷載作用下不可避免的沉降性，須采取一定工程措施。當(dāng)超過3個凍融循環(huán)時，路基沉降量明顯增長，原因在于凍融造成的直接變形雖然已經(jīng)被消除，但凍融作用的強(qiáng)烈風(fēng)化作用卻依然存在，隨著凍融循環(huán)次數(shù)的增加，填筑材料的風(fēng)化效果逐漸顯現(xiàn)，導(dǎo)致結(jié)構(gòu)發(fā)生變化，結(jié)構(gòu)強(qiáng)度降低，路基沉降量明顯增長，到達(dá)第5個凍融循環(huán)結(jié)束時，累積沉降值已經(jīng)達(dá)到7.6 mm。為了避免出現(xiàn)或推遲該現(xiàn)象的出現(xiàn)，應(yīng)該做好路基的防水準(zhǔn)備，隨著時間的推移，累積沉降值逐漸趨于一穩(wěn)定狀態(tài)。

5 結(jié)論

本文利用數(shù)值分析軟件Midas研究預(yù)測了嚴(yán)寒地區(qū)某鐵路線路基在凍融循環(huán)和列車荷載作用下10年內(nèi)的累積沉降量，得出以下幾點(diǎn)結(jié)論。

(1)對于地基粉黏土來說，很容易受凍融的影響，凍結(jié)期和融化期的物理力學(xué)性質(zhì)相差很大，需在修筑時采取地基加固措施；而填土受凍融影響較小，這說明路基填筑材料具有較好的防凍性能；隨著凍融次數(shù)的增加對于地基粉黏土和填土來說，其變形模量和黏聚力是減小的，其摩擦角是增大的。

(2)路基累積沉降值隨凍融次數(shù)的增加而增大，前3次凍融循環(huán)路基沉降量增長緩慢，從第4次凍融循環(huán)開始，路基沉降量明顯增長，故建議路基在修筑完成后第3年時加強(qiáng)對路基的養(yǎng)護(hù)和維修。

(3)路基融化狀態(tài)下的沉降值比凍結(jié)狀態(tài)下的沉降值大，這與理論相符，在路基融化時期更要加強(qiáng)對道路的養(yǎng)護(hù)。

[1] 徐學(xué)祖，鄧友生.凍土中水分遷移的實(shí)驗(yàn)研究[M].北京:科學(xué)出版社，1991．

[2] 張婷.人工凍土凍脹融沉特性研究[D].南京：南京林業(yè)大學(xué)，2004．

[3] 李東升.嚴(yán)寒地區(qū)客運(yùn)專線路基穩(wěn)定性的研究[D].石家莊：石家莊鐵道大學(xué)，2012．

[4] 何平，程國棟，楊成松，等.凍土融沉系數(shù)的評價方法[J].冰川凍土，2003，25(6):608-613．

[5] 王建平，王文順.人工凍結(jié)土體凍脹融沉的模型試驗(yàn)[J].中國礦業(yè)大學(xué)學(xué)報，1999，28(4)：303-306．

[6] 尚松浩，雷志棟，楊詩秀.凍結(jié)條件下土壤水熱耦合遷移的數(shù)值模擬的改進(jìn)[J].清華大學(xué)學(xué)報，1997，37(8):62-64．

[7] 孔祥輝，蔣關(guān)魯.循環(huán)荷載下紅層泥巖路基土的變形特性研究[J].鐵道標(biāo)準(zhǔn)設(shè)計，2013 (2):1-4．

[8] 王鐵行，胡長順.考慮多種因素的凍土路基溫度場有限元方法[J].中國公路學(xué)報，2000，13(4):8-11．

[9] 王平.青藏鐵路多年凍土區(qū)凍脹丘發(fā)展特征及其對路基穩(wěn)定性的影響[J].鐵道標(biāo)準(zhǔn)設(shè)計，2013 (5):1-4．

[10] 胡和平，楊詩秀.土壤凍結(jié)時水熱偶爾遷移的數(shù)值模擬[J].水利學(xué)報，1992(7):1-8．

[11] 喻文兵，賴遠(yuǎn)明，牛富俊，等.多年凍土區(qū)鐵路通風(fēng)路基室內(nèi)模型試驗(yàn)的溫度場特征[J].冰川凍土，2002，24(5):601-607．

[12] 張學(xué)富，賴遠(yuǎn)明，喻文兵，等.寒區(qū)隧道三維溫度場的數(shù)值分析[J].鐵道學(xué)報，2003，25(3):84-91．