樁基礎支撐的周期性高架橋結構的缺陷態研究

陸建飛,雷 力

(江蘇大學土木工程系,江蘇鎮江 202013)

高速鐵路是一個地區乃至整個國家的生命工程線。高速鐵路對地基沉降有嚴格的要求,而高架橋恰能有效解決軟土地基不均勻沉降的問題,因此,高架橋結構在高速鐵路建設中得到了廣泛應用。例如,京滬高速鐵路中多數路段均采用高架橋結構[1]。為便于施工,高架鐵路的常規路段常設計成由相同的橋跨構成,因此,上述高架鐵路可簡化為周期性結構。然而,由于地理環境等因素的影響,在工程實際中也常使得高架橋結構的某一跨或相鄰幾跨在材料或幾何參數與標準跨不一致。根據周期性理論,上述與標準跨不一致的跨為高架橋結構的一種缺陷。在本文中,將不同于標準跨的跨定義為缺陷跨,稱包含缺陷跨的周期性高架橋為缺陷周期性高架橋。

波在周期性結構中傳播可追溯到1883年Floquet對一維Mathieus’s方程的研究。Mead、Lin等人對波在周期性梁類結構中傳播的研究表明,規則的周期性結構具有“通頻”和“禁頻”特性[2-5]。通常缺陷能改變周期性結構的波動特性,因此,波在含缺陷周期性結構中傳播比在標準周期性結構中傳播更為復雜。例如,Sigalas[6]的研究表明缺陷使得周期性結構產生了額外的能帶,且其波動局域在缺陷處。吳福根[7]對二維周期性結構的研究表明,當頻率為缺陷頻率時,缺陷態壓強在結構的缺陷處呈現出極大值。后來,Khelif[8]從理論和實驗上研究了周期性結構的缺陷態特性,均得到與上述理論相吻合的結果。

雖然目前存在一些關于周期性結構缺陷態的文獻[5-8],但現存的研究均局限于周期性連續梁結構,對簡支梁型的周期性結構缺乏研究。正如工程實際中的高架橋由單獨梁組成,并通過橋墩和樁基礎支撐,因而把高架橋結構簡化為連續梁是不合理的。再者,由于目前尚未建立缺陷周期性梁類結構的超原胞方法,故對其超原胞的缺陷態也缺少研究。

本文主要目的是建立一個數值計算模型,求解簡支梁型周期性高架橋結構缺陷態。本文的主體框架如下所述：為獲得樁基礎的柔度,首先利用邊界元方法處理樁-土相互作用問題；然后,利用所得樁基礎的柔度,梁和墩的傳遞矩陣及梁-梁-墩接頭的聯結條件,推導高架橋單跨的傳遞矩陣。基于超原胞的思想,建立了求解高架橋結構缺陷態的超原胞方法。最后,文中給出了樁基礎支撐的周期性高架橋結構的缺陷態。

1 樁-土相互作用的邊界元模型

在工程實際中,高架橋的每跨包含一個或多個橋墩,而每個橋墩由群樁基礎支撐。為了簡化,假設高架橋的每跨只包含一個橋墩,且高架橋的樁基礎由單樁組成,高架橋的樁與橋墩之間為剛性聯結,高架橋每跨中的梁與梁及梁與橋墩之間均通過彈簧連接。基于上述假設,周期性高架橋的每跨可簡化為由單根樁基礎,1個橋墩,左、右橫梁及3根聯結彈簧所組成的單元(圖1)。另外,本節將建立樁-土耦合邊界元模型處理樁-土相互作用問題。

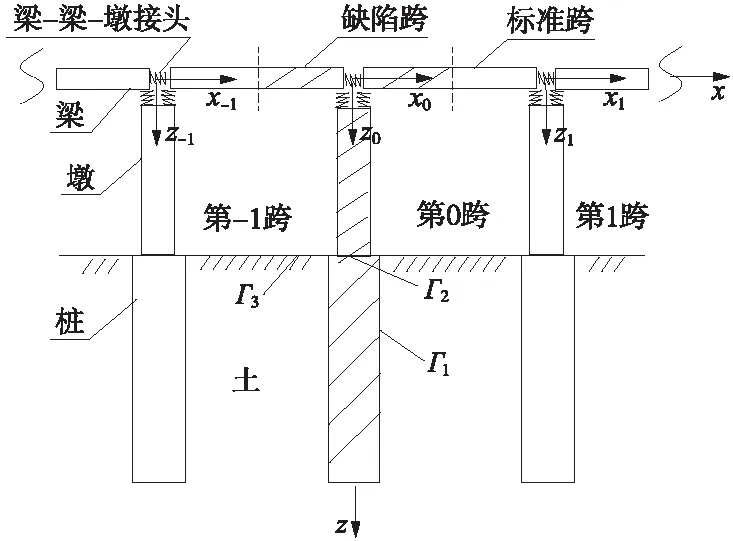
圖1 含缺陷周期性高架橋結構示意

1.1 彈性介質的邊界積分方程

在本文中,把樁和土體均處理成彈性介質。彈性介質在頻域內的運動方程為[9]

μui,jj+(λ+μ)uj,ji=-ρω2ui(1)

式中,λ和μ為彈性介質的拉梅常數；ui和ρ分別為彈性介質的位移和密度；ω為角頻率。另外,彈性介質的本構關系為[9]

σij=2μεij+λδije(2)

式中,σij和εij分別為彈性介質的應力和應變分量；e和δij分別為體積應變和內羅內克符號。基于動力互易定理, 彈性介質在頻域內的邊界積分方程為[10]

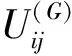
1.2 樁-土耦合邊界元模型

在本節中,依據彈性介質的邊界積分方程推導了樁和土體的邊界元公式,并基于上述公式建立了樁-土耦合邊界元模型。在如圖1所示的樁-土耦合系統中存在3種邊界面：樁和土體相交的界面為邊界面Γ1；樁頂部為邊界面Γ2；土體表面為邊界面Γ3。

利用樁的邊界積分方程,可得樁的邊界元公式為

H(p)u(p)=G(p)t(p)(4)

式中,上標p代表樁；u(p)和t(p)分別為樁邊界面上單元節點的位移向量和面力向量；G(p)和H(p)代表系數矩陣。公式(4)可重新推導為

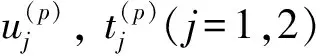
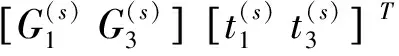
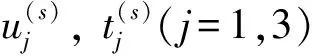
在樁和土體的邊界面Γ1和Γ3上,有如下連續性和邊界條件成立

(7)

基于公式(5)到(7),可得樁-土耦合邊界元模型為

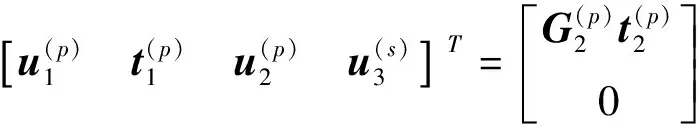
高架橋結構發生面外振動時,樁頂部有扭矩,剪力和彎矩作用。設高架橋第n號樁頂部的位移向量和力向量可分別表示為

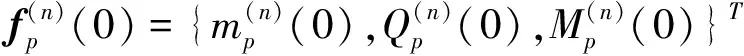
(10)

式中,Cp為樁基礎的柔度矩陣。

2 周期性高架橋單跨的傳遞矩陣

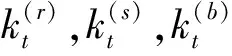
為便于描述高架橋第n跨的響應,在第n跨上建立如圖1所示的局部坐標系。由于本文只考慮高架橋結構的面外振動,這里的梁和墩將產生扭轉及面外彎曲振動,因此,梁和墩的傳遞矩陣可利用桿件的扭轉振動和Bernoulli-Euler梁的彎曲振動理論推導。高架橋第n跨中的梁在扭轉和面外彎曲振動下的控制方程分別為[11]

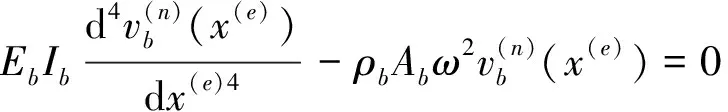
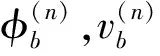
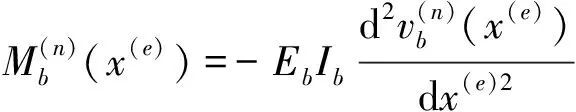
高架橋第n跨任意梁截面的狀態向量可表示為

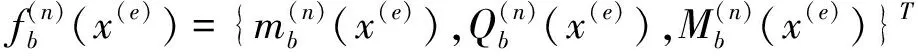
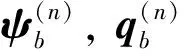
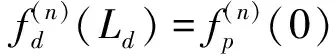
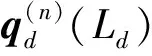
(15)

式中,Ld為橋墩的高度。

忽略3根聯結彈簧質量,并利用公式(13)到(15)、梁-梁-墩接頭處的平衡條件、彈簧的本構關系及墩的傳遞矩陣,可得高架橋第n跨梁-梁-墩(BBP)接頭的左、右兩端梁截面的狀態向量所滿足的關系式為

(16)

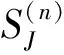
利用梁和BBP接頭的傳遞矩陣及傳遞矩陣方法[13],可得高架橋第n跨左、右兩端梁截面的狀態向量所滿足的關系式為

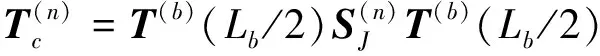
3 含缺陷周期性高架橋的超原胞方法及缺陷態

由連續介質組成的聲子晶體中的缺陷會使其產生缺陷態[5-8],這里的周期性高架橋結構可認為是一種聲子晶體結構。值得指出的是,目前尚未有文獻研究簡支梁型周期性結構的缺陷態。因此,本文基于超原胞的思想,建立缺陷高架橋結構的超原胞方法,求解周期性梁類結構的缺陷態。

為實施缺陷高架橋結構的超原胞方法,首先須選定含缺陷跨的超原胞,且超原胞包含的跨數必須使得缺陷態模態所對應的響應在超原胞的端部趨于零。設含缺陷周期高架橋的超原胞由2n+1跨組成,且中間跨為缺陷跨(第0跨),利用高架橋標準跨及缺陷跨的傳遞矩陣,可得超原胞兩端的狀態向量所滿足的關系式為

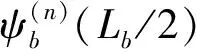
基于Bloch定理[14]和公式,可得高架橋超原胞的特征方程為

(19)

式中,LS=2nLb+L0為超原胞的長度；L0為缺陷跨的長度；κ為高架橋超原胞中的特征波波數。

4 數值結果和分析

基于公式(19),可得含缺陷周期性高架橋超原胞的缺陷態。在算例中,將考慮缺陷跨的梁和橋墩存在缺陷對高架橋的影響。假設樁和橋墩的橫截面均為圓形,梁的橫截面為矩形。對于標準跨,各參數的取值如表1所示。對于缺陷跨,與標準跨不一致參數的取值如下所示：橋墩的半徑為0.5 m；右梁橫截面高、寬分別為0.6 m和2.0 m,右梁的楊氏模量為2.2×1010Pa。

表1 樁、土、橋墩、梁和彈簧剛度等參數取值

注：BBP接頭把梁為左、右梁

如圖1所示的周期性高架橋在面外振動下存在3種特征波,由于第一、二種特征波是衰減波,因此,本文僅給出第三種特征波的結果。圖2為高架橋超原胞中第三種特征波的能帶。從圖2(b)可知,頻率5.0 Hz位于標準超原胞(15跨均為標準跨)的禁帶內,但其又位于缺陷超原胞(由15跨組成,且中間一跨為缺陷跨)的通帶內,這表明頻率5.0 Hz為缺陷高架橋超原胞的缺陷態頻率。顯然,這個附加的通帶頻率由高架橋結構中含缺陷跨所引起。對于標準和缺陷超原胞,圖2(b)還顯示第三種特征波的虛部在高頻范圍內均很大。

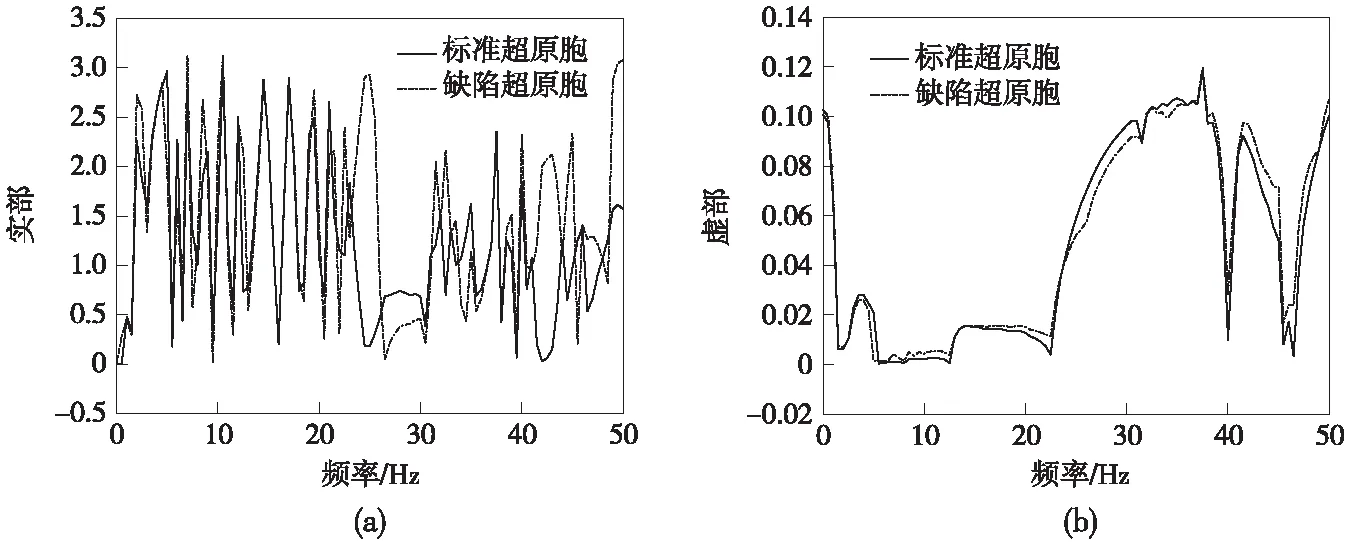
圖2 超原胞中第三種特征波的能帶

圖3給出了超原胞內各跨梁左端和墩底在缺陷頻率處的模態。圖3(a)顯示扭轉角在缺陷跨兩端的響應明顯大于超原胞的其他跨,且遠離缺陷跨的響應很小。對于超原胞內各跨墩底的扭轉角,上述現象表現更為明顯(圖3(b))。此外,缺陷超原胞的模態還表明：波動局域在缺陷跨附近,并通過缺陷跨放大,類似于固體力學中的應力集中現象。

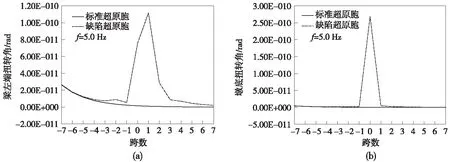
圖3 超原胞在缺陷頻率5.0 Hz處的模態

5 結論

本文建立了簡支梁型周期性高架橋結構缺陷態計算模型,建立了計算高架橋結構缺陷態的超原胞方法。在模型中,引入聯結彈簧把高架橋的梁-梁-墩接頭處理成彈性接頭。本文的計算結果表明，缺陷會使周期性高架橋結構產生額外的能帶,即缺陷態；當頻率為缺陷態頻率時,超原胞的缺陷態模態在高架橋的缺陷跨處產生了顯著的應力集中現象,顯然,這對周期性高架橋結構的受力是極為不利的。本文所建立的模型可應用于求解高架橋支撐在層狀地基上的缺陷態,還可推廣用于處理高架橋結構含多個相鄰缺陷跨的情形。

附錄A：公式(16)的表達式

公式(16)中矩陣A和B的表達式為

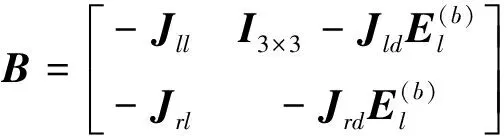
式中,

其中,Cd為橋墩的柔度矩陣,即

(A.2)

[1] 孫樹禮.京滬高速鐵路橋梁工程[J].鐵道標準設計,2008(6)：1-4．

[2] Mead D J. Free wave propagation in periodically supported infinite beams[J]. Journal of Sound and Vibration, 1970,11(2):181-197．

[3] Mead D J, Markus S. Coupled flexural longitudinal wave motion in a periodic beam [J]. Journal of Sound and Vibration, 1983,90(1):1-24．

[4] Lin Y K. Free vibrations of a continuous beam on elastic supports [J]. International Journal of Mechanical Sciences, 1962,4(5):409-423．

[5] 溫熙森,等.聲子晶體[M].北京：國防工業出版社,2009．

[6] Sigalas M M. Elastic wave band gaps and defect states in two-dimensional composites[J]. Journal of Acoustical Society of America, 1997,101(3):1256-1261.

[7] 吳福根,劉有延.二維周期性復合介質中聲波帶隙結構及其缺陷態[J].物理學報,2002,51(7)：1434-1438．

[8] Khelif A, et al. Trapping and guiding of acoustic waves by defect modes in a full-band-gap ultrasonic crystal[J]. Physical Review B, 2003,68(1):214301．

[9] Achenbach J D. Wave Propagation in Elastic Solids[M]. Amsterdam: North-Holland, 1973．

[10] Banerjee P K, Butterfield R. Boundary Element Methods in Engineering Science[M]. UK: McGraw-Hill, 1981．

[11] Graff K F. Wave Motion in Elastic Solids[M]. Oxdord: Clarendon Press, 1975．

[12] Lu J F, Jeng D S. Energy bands of a periodic viaduct in out-of-plane vibration: Coupling with a half-space[J]. Europuean Journal of Mechanics-A/Solids, 2012,31(1):21-36．

[13] Dowling J P. Sonic Band structure in fluids with periodic density variations[J]. Journal of the Acoustical Society of America, 1992,91(5):2539-2543．

[14] 閻守勝.固體物理基礎[M].北京：北京大學出版社,2011．