大樁帽軌道梁不同支承條件的受力分析

陶桂蘭，卜美飛

（河海大學港口海岸與近海工程學院，江蘇 南京 210098）

1 問題的提出

隨著裝卸設備的大型化及碼頭向外海發展，為滿足結構的使用要求及抵抗施工期的波浪作用，縱、橫梁節點處的樁數增多，工程上常在節點處采用大樁帽結構，樁帽上擱置預制梁并現澆梁節點，因此梁的支座寬度較以往大大增加，有些碼頭軌道梁的支座寬度已達到梁中到中跨度的0.6倍左右[1]。JTJ267—98《高樁碼頭設計與施工規范》（以下簡稱98規范）在梁內力計算中，將縱梁簡化為彈性支承連續梁或剛性支承連續梁計算，彈性支承連續梁法支座處采用點支承，無法考慮支座寬度的影響。現行JTS167-1—2010《高樁碼頭設計與施工規范》（以下簡稱2010規范），考慮到目前高樁碼頭的發展趨勢，在規范中提出了軌道梁寬支座計算方法，采用支座內的分布彈簧模擬寬支座的影響。但寬支座梁的受力特性如何，新老規范不同支承條件對軌道梁內力的影響仍是工程界極為關心的問題。本文以某大樁帽碼頭為例，模擬高樁碼頭中的縱向軌道梁排架，利用Ansys軟件對模型進行有限元模擬，得到縱梁在采用大樁帽時的一些受力特性，并對軌道梁不同支承條件下的受力特性進行了比較分析，以供類似工程設計參考[2-3]。

2 計算模型

2.1 工程概況

本文計算結構以上海某碼頭后門機軌道梁為例，縱梁全長78 m，共6個排架，排架間距12 m，兩端各有3 m長的懸臂段，縱梁使用期截面尺寸為1.6 m×2.75 m，樁帽尺寸為6.3 m×5.4 m×2.1 m。縱梁及樁帽材料為混凝土C45，彈性模量E=3.35×104MPa，泊松比μ=0.167。樁基為鋼管樁，樁自由長度為12.4 m，外徑1.2 m，壁厚0.02 m，彈性模量E=2.1×105MPa，泊松比μ=0.3。每個樁帽下設有3根斜樁，斜樁傾斜度為6∶1。軌道梁結構示意圖見圖1。

圖1 軌道梁結構示意圖（單位：m）

2.2 計算模型

本文考慮《98規范》及《2010規范》中軌道梁的3種支承方式及寬支座梁空間有限元模型對寬支座軌道梁進行計算分析，計算模型均采用ANSYS有限元軟件建模。

1）剛性點支承連續梁模型

該計算模型中的軌道梁采用beam188單元，支座處節點的豎向自由度約束，3個轉動自由度自由。有限元模型見圖2。

圖2 剛性點支承連續梁有限元模型圖

2）彈性點支承連續梁模型

模型中的軌道梁采用beam188單元，支承處用彈簧單元combin14模擬彈性點支承，彈簧與梁單元連接點處進行節點耦合，彈簧底端全部固定。彈簧常數取所在支座處的剛性系數，計算得k=1.303×106kN/m。有限元模型見圖3。

圖3 彈性點支承連續梁有限元模型圖

3）分布彈性支承計算模型

當以支座寬度范圍內有限個等間距布置的彈簧代替均勻分布彈簧時，單個彈簧的剛性系數可按下式計算：

式中：kn為單個彈簧剛性系數，kN/m；K為支座豎向剛性系數，kN/m，取樁帽在支座中心處產生單位豎向位移時所需豎向作用力的數值；n為支座寬度范圍內等間距布置的彈簧個數。

模型中的縱梁選取beam188單元，選取彈簧單元combin14來模擬彈性支承，每個支座寬度范圍內均勻布置28個彈簧，每個彈簧常數相同。經計算取支座豎向剛性系數為k=1.303×106kN/m，可得單個彈簧常數為k=46 530 kN/m。彈簧與梁單元連接點處進行節點耦合，彈簧底端全部固定，模型有限元圖見圖4[4-5]。

4）空間有限元計算模型

為便于比較不同計算模型對內力的影響，本文同時建立了縱向排架空間有限元計算模型。縱梁采用beam188單元，樁帽選用實體單元solid45模擬，樁基采用管單元pipe16，樁與樁帽采用固接連接，樁端與土之間彈性嵌固，經計算，嵌固深度取4.6 m。梁單元和樁帽實體單元連接處采用節點耦合，樁端與土之間用彈簧單元combin14來模擬，樁與彈簧單元連接點處除樁軸向自由度外，其他自由度全部約束，彈簧底端固接。有限元模型見圖5[4-5]。

圖5 縱向排架空間有限元模型圖

3 計算結果分析

計算時采用均布荷載，荷載值取q=151kN/m。各計算模型彎矩、剪力圖對比見圖6、圖7，考慮到模型以及荷載的對稱性，文中只給出半梁彎矩、剪力圖。（圖中坐標軸黑線部分表示樁帽段）：

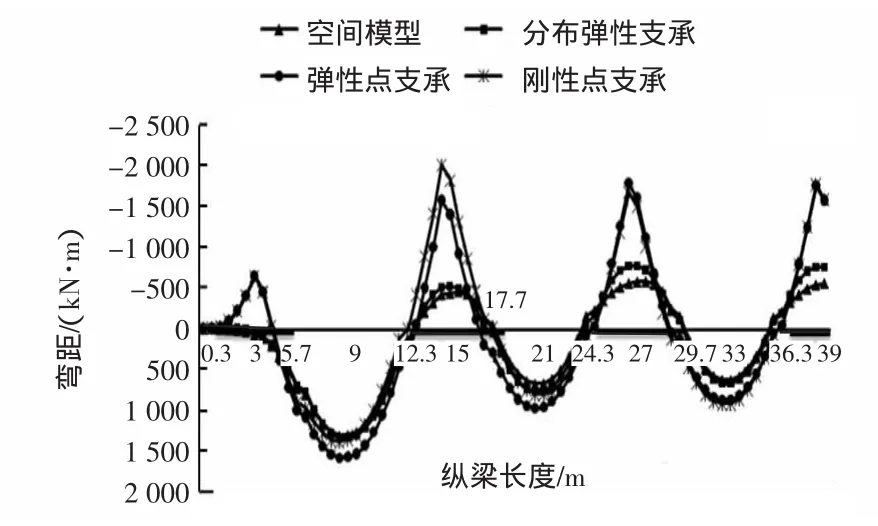
圖6 不同計算模型軌道梁彎矩比較

圖7 不同計算模型軌道梁剪力比較

各模型的最大正負彎矩以及最大剪力見表1。

3.1 彎矩分布特性

由彎矩圖及表1可知：彈性點支承連續梁計算所得的最大負彎矩小于剛性點支承連續梁，而最大正彎矩大于剛性點支承連續梁。彈性點支承模型計算所得的最大正彎矩、最大負彎矩、最大剪力要比分布彈性支承計算所得結果要大的多，特別是最大負彎矩達到2.3倍，表明支承寬度對連續梁的內力有明顯的削峰作用，特別是最大負彎矩。

表1 各計算模型最大正負彎矩以及剪力

從支座邊緣處的彎矩比較可以看出，兩種點支承模型與分布彈性支承模型以及空間模型在支座左邊緣處的彎矩符號完全相反，表明如果樁帽寬度比較大時，對點支承模型進行支座處彎矩削峰后取支座邊緣處彎矩作為控制彎矩有可能產生較大的誤差。

從分布彈性支承與空間模型彎矩圖比較可知，兩種模型的計算結果比較接近，本例計算結果表明，空間模型計算所得支座邊緣處的最大負彎矩比分布彈性支承模型略大，而支座中心處的最大負彎矩比分布支承模型略小，即空間模型的支座彎矩在支座范圍內更為均勻。

3.2 剪力分布特性

從剪力值計算結果可以看出，剛性點支承模型計算所得最大剪力大于其它3種模型，剛性點支承模型支座邊緣處的剪力值最大，空間模型和分布彈性支承模型計算結果比較接近，4種計算模型支座邊緣處的剪力差別不大。

3.3 支座反力分布特性

分布彈性支承、空間模型各支座反力分布見圖8，考慮到結構的對稱性，文中給出前四個樁帽處的支座反力分布圖。

從各支座反力分布圖可知，分布彈性支承與空間模型支座處反力分布差距較大，分布彈性支承支座處的反力分布基本呈均勻分布，而空間模型支座兩端反力較大，支座中間反力較小，呈拋物線分布。支座反力分布應與支承模型假定有關，有待于進一步討論。

圖8 各支座反力分布圖

4 主要結論

本文以某寬支座梁為例，通過ANSYS軟件對寬支座梁的4種模型：彈性點支承，剛性點支承，分布彈性支承以及空間模型進行有限元模擬，得出不同模型下的連續梁內力以及支座反力的分布特性，并對不同模型的計算結果進行比較，得到以下主要結論：

1）對于大樁帽軌道梁，按彈性點支承模型及剛性點支承連續梁模型計算彎矩與寬支座梁分布模型計算其支座邊緣處的彎矩有較大差異，對寬支座梁采用彈性點支承模型連續梁計算彎矩后再削峰的方法將可能產生較大的誤差。

2）計算表明支座寬度對連續梁的內力有明顯的削峰作用，特別是最大負彎矩，因此對大樁帽梁計算時有必要考慮寬支座的影響。

3）對于大樁帽梁，按彈性和剛性點支承連續梁模型計算支座中心截面剪力與分布彈性支承模型及空間模型計算值差異較大，支座邊緣處剪力值與分布彈性支承模型及空間模型的計算結果比較接近。

4）分布彈性支承模型與空間模型的內力計算結果比較相近，但空間模型與分布彈性支承模型在各支座處的反力分布相差較大，對于支座反力計算模型，有待于進一步討論。

[1] 周偉才.大樁帽碼頭排架計算方法及模型試驗研究[D].南京：河海大學，2005.

[2] 曹稱宇.寬支座條件下梁的內力計算研究[D].南京：河海大學，2005.

[3] 周偉才，陶桂蘭.考慮節點域和剪切變形影響的高樁碼頭橫向排架的內力計算[J].水利水運工程學報，2005（1）：56-59.

[4] 王新敏.ANSYS工程結構數值分析[M].北京：人民交通出版社，2007：230-407.

[5] 陸東漢.用寬支承方式計算高樁梁板式碼頭上的軌道梁[J].水運工程，2003（12）：36-39.