高速鐵路軌道基準網平面網精度指標合理性研究

林遠胡，劉成龍，蒲星鋼，楊雪峰

(西南交通大學地球科學與環境工程學院，四川成都 610031)

高速鐵路軌道基準網平面網精度指標合理性研究

林遠胡，劉成龍，蒲星鋼，楊雪峰

(西南交通大學地球科學與環境工程學院，四川成都 610031)

介紹國外對高速鐵路軌道基準網平面網精度的評定方法，通過試驗和客運專線實測數據研究軌道基準點相對點位精度指標的合理性，并結合某客運專線實測數據對平面網外業數據的限差指標進行統計分析。研究結果表明：將軌道基準網平面網相鄰點相對點位精度定為0.2 mm偏高，現有的測量方法難以達到，合理值應為0.4 mm;外業測量時還應增加各點多次測量間坐標較差作為控制指標，以彌補目前平面網只有內業數據處理限差指標的不足。

軌道基準網 軌道基準點 相對點位中誤差 精度評定

軌道基準網(TRN)是軌道控制網(CPⅢ)下的一級加密控制網，由一系列的軌道基準點(TRP)組成。TRP布設于6.5 m間隔的軌道板板縫之間，為軌道板的精調提供基準，因此，其精度將直接影響到軌道板的精確定位。TRN的精度要求極高，國外要求其平面網相鄰TRP間的相對點位中誤差應＜±0.2 mm，高程網相鄰TRP間的高差中誤差應＜±0.1 mm。

國外關于TRN平面網精度要求0.2 mm有如下定義：在一測站內測量TRP平面坐標時，各TRP是相對于測站本身的離散支點，視其多次測量坐標的均值為真值，各次TRP坐標重復測量值與其均值之最大橫向偏差規定為0.3 mm，即限差為0.3 mm。一般取限差的1/2為中誤差，即中誤差為0.15 mm，因此本測站內相鄰TRP間的相對點位中誤差為×0.15=0.21 mm。由于縱向偏差對平順性的影響相對較小，故各次重復測量值與其均值之最大縱向偏差規定為0.4 mm。

國外宣稱通過嚴格控制外業測量中的偏差，精度要求就能達到。由于缺少相應的精度評定方法和模型，能否達到這么高的精度要求值得探討。

本文首先介紹一種國外TRN平面網精度評定方法，然后通過仿真試驗及對試驗數據進行處理與分析，以檢驗TRN平面網精度＜0.2 mm這一要求的合理性，最后統計了某客運專線120 km長TRN平面網的實測數據及其精度，對TRN平面網的精度指標進行分析，并據此提出了合理的TRN平面網的精度指標。

1 相鄰TRP間相對點位中誤差計算原理

國外的TRN平面網平差計算之前，需對外業成果進行檢核：即計算TRP單次坐標觀測值與多次坐標均值的較差，其限差要求如表1所示。

表1 TRP平面坐標值與其均值較差的限差 mm

當一測站所測量3次的n個TRP的坐標滿足表1所示限差要求后，可在一個測站范圍內進行相鄰TRP間相對點位中誤差的計算，計算原理如下：

根據每站的各n個TRP在站心坐標系下的坐標，按照坐標反算公式可計算出這個測站n－1段相鄰TRP間的3個距離Sij和3個坐標方位角αij(i=1，2，…，n－1;j=2，3，…，n);接著可計算它們兩兩間的距離較差ΔSij和坐標方位角較差Δαij，由于每相鄰TRP間獨立的距離較差和坐標方位角較差各有2個，則一個測站內就有2(n－1)個距離較差ΔSij和2(n－1)個坐標方位角較差Δαij。

根據測站離相鄰TRP間的測段越遠，則由該測站測量該測段的距離和方位角的精度就越差這一規律，可確定各測段距離和方位角測量的權。由于每測站TRP平面坐標測量時，測站至最遠TRP的距離一般不會超過100 m，故可假設TRP平面坐標測量時測站到100 m處的相鄰TRP間的距離和方位角測量為單位權觀測，則各相鄰TRP間距離和方位角測量的權Pij可按下式計算

式中，Si，Sj分別為測站到相鄰的第i和第j個TRP的距離，m。

根據同一測站內的2(n－1)個距離較差ΔSij和2(n－1)個坐標方位角較差Δαij及其權Pij，就可按單位權中誤差計算公式，計算該測站距離測量的單位權中誤差μ距和方位角測量的單位權中誤差μ方。

由于同一測站同一段相鄰TRP間的距離和方位角各次測量的方法完全相同，因此可認為同一測站相鄰TRP間的距離和方位角各次測量的中誤差是相同的，故可按照下式計算相鄰TRP間距離測量中誤差msij和方位角測量的中誤差mαij：

由于最終是取3次TRP測量坐標的均值，作為本測站各TRP的最后坐標，因此還應計算相鄰TRP間最后距離均值測量的中誤差msij和方位角均值測量的中誤差

最后可由式(3)計算相鄰TRP間的相對點位中誤差［2］

2 試驗及結果分析

為分析判斷平面網相鄰TRP間的相對點位中誤差＜0.2 mm這一精度指標的合理性，在模擬高鐵的試驗場地上進行了平面網測量的試驗，并對試驗數據進行處理分析，同時還統計分析了某客運專線120 km長軌道基準網實測數據的精度。

2.1 試驗概況

試驗場地上TRN嚴格按照高速鐵路的規定布設，左右線共布設有5對CPⅢ點及20對TRP，CPⅢ點間距為60 m左右，TRP點間距為6.5 m左右，為確保試驗精度，CPⅢ點和TRP均采用強制對中標志。試驗場地點位布設如圖1所示。

圖1 試驗場地點位布設示意

試驗所用全站儀型號為徠卡TCRA1201+，其標稱精度為：方向中誤差±1″和測距中誤差±(1 mm+2D×10－6)，其中D為距離，km。本試驗只對右線一個測站的10個TRP進行多次坐標測量，測量過程為：儀器設在右線軌道中心線上，然后由遠及近對14個TRP進行正鏡位半盤位觀測，每3次半盤位作為1組，試驗重復進行10組，測量過程中全站儀始終保持不動且保證最遠點離測站距離在100 m內。

2.2 試驗結果分析

按照上文介紹的相鄰TRP間的相對點位中誤差計算方法對試驗觀測數據進行精度評定計算，得到10組測量的精度數據，統計結果見表2。

由表2可以看出，在重復觀測的10組數據的相鄰點相對點位精度中：僅有3組的相鄰點位中誤差滿足±0.20 mm的精度指標要求，最小值為0.11 mm;其余各組數據中，離測站最遠兩點間的相對點位精度均超出0.20 mm，最大值達到0.31 mm;各組的相鄰點位精度的平均值最大值為0.26 mm，最小值為0.14 mm。試驗結果說明相鄰TRP的相對點位精度不能完全滿足0.20 mm精度要求。

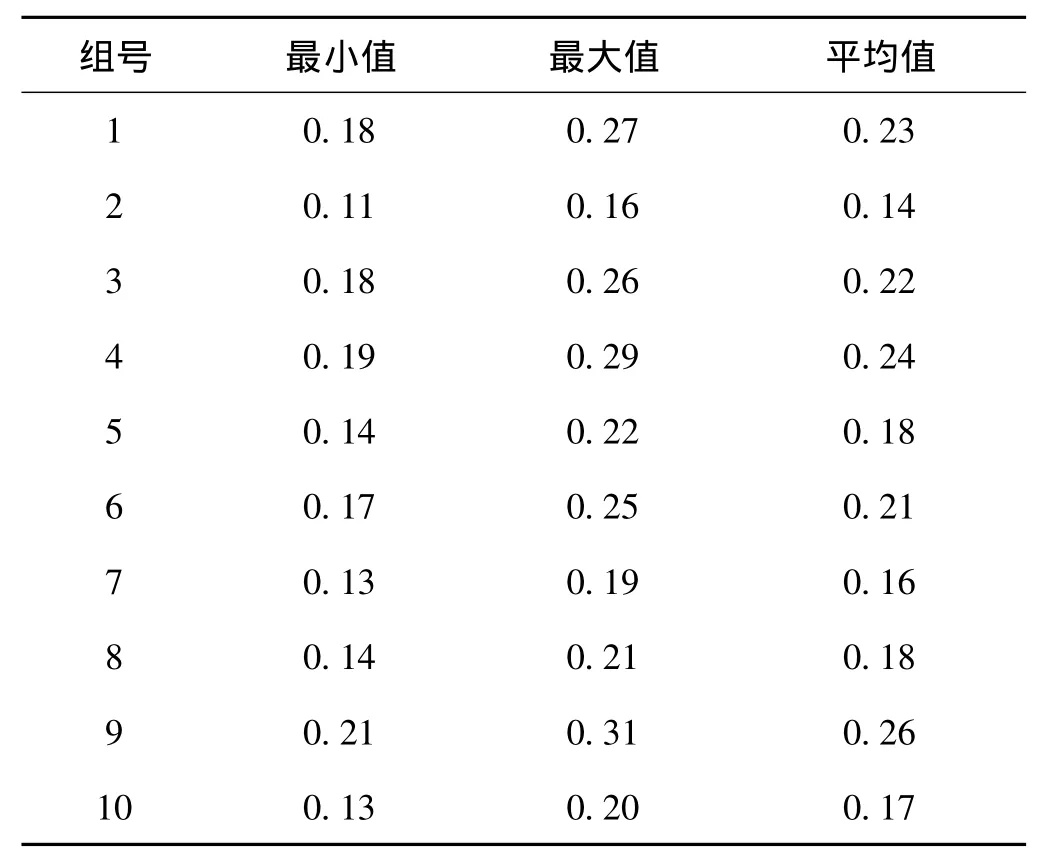
表2 相鄰TRP間相對點位中誤差統計 mm

2.3 實測數據分析

根據國外平面網坐標測量的精度要求，按照前文介紹的方法，對某客運專線120 km長的TRN平面網實測數據進行了精度計算，統計結果見表3。

表3 實測數據相鄰TRP相對點位中誤差統計

從表3中可以看出，在統計的21 552個相鄰點的相對點位中誤差中，在0.2 mm以內的數據只占總數的66.61%，而在0.3 mm內和0.4 mm內的數據分別占總數的94.73%和98.87%。可見，將相鄰點相對點位精度定為0.2 mm偏高，現有的軌道基準網測量方法難以達到要求。根據試驗結果和對實測數據精度的統計分析，該值定為0.4 mm較為合理。

3 多次測量坐標與其均值較差分析

TRN內業數據處理時，各TRP均需滿足表1所示限差要求，可見TRP多次測量坐標與其均值較差的限差，應當作為內業數據處理的依據。下面將從相鄰點的相對點位中誤差出發并結合某客運專線實測數據的統計分析，對TRP多次測量坐標與其均值較差的限差指標的合理性進行驗證。

在一測站內，假設離測站最遠的TRP為P1，坐標為(x1，y1)，次遠 TRP 為 P2，坐標為(x2，y2)，這兩點的相對位置可通過坐標差Δx12和Δy12來表示，即

由式(4)，根據協因數傳播律，可得P1和P2在x，y 方向坐標差的協因數 QΔxΔx和 QΔyΔy分別為

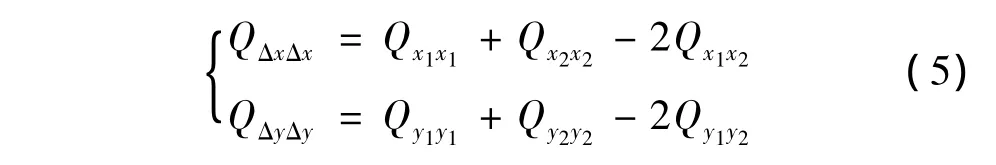
式中，Qx1x1和Qx2x2分別為P1和P2在x方向的坐標協因數;Qy1y1和Qy2y2分別為P1和P2在y方向的坐標協因數;Qx1x2和Qy1y2分別為P1和P2在 x方向和y方向的互協因數。

式中，σ0為驗后單位權中誤差。

由于同一測站觀測的所有TRP均為相對于該測站的散點，在忽略二者與測站距離不相等的情況下，可認為P1與P2坐標誤差不相關且點位中誤差與MP2相等(記為MP)，則由式(6)可得

則P1點多次測量坐標差的中誤差MΔP1為

由于MΔP1受P1點的x坐標差和y坐標差共同影響，假設兩者影響相同，則P1的多次測量x坐標差和y坐標差的中誤差MΔP1X和MΔP1Y為

以2倍中誤差為限差，則P1點多次測量x坐標差dPX的限差ΔPX和y坐標差dPY的限差ΔPY分別為

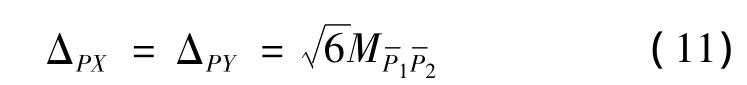
由于TRP通常觀測3次，則由式(11)可得P13次測量x，y坐標與其均值較差Δ'PX、Δ'PY的允許值為

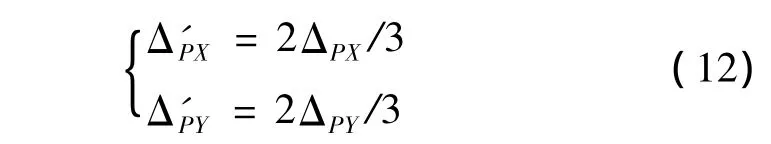
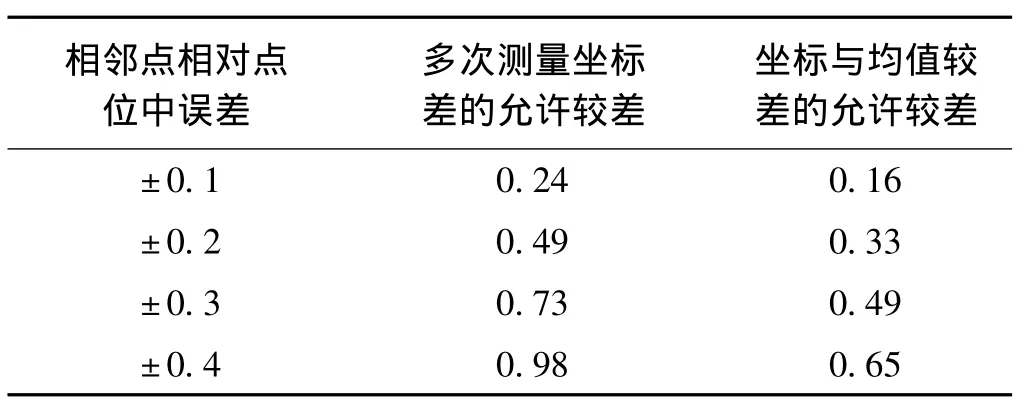
表4 多次測量坐標差的允許較差和坐標與均值較差的允許較差估值 mm

從表4可看出：當相鄰TRP相對點位中誤差為±0.2 mm時，對應的多次測量坐標與均值較差的允許較差為0.33 mm。而國外規定的多次測量x，y坐標與其均值較差限差分別為0.30 mm和0.40 mm，這與估算的0.33 mm吻合得較好。下面依據某客運專線實測數據多次測量坐標與均值較差的統計結果，來進一步探討這一指標的合理性。

基于表4計算的估值數據，對某客運專線120 km TRP實測數據的多次測量x，y坐標與其均值較差(絕對值)進行統計，見表5。

表5 實測數據多次測量坐標與其均值較差統計

可見，在統計的83 364個多次測量x，y坐標與其均值較差絕對值數據中：x較差和y較差在0.33 mm以內的數據分別有80 648個和80 683個，占總數的96.74%和96.78%。綜上可知：國外規定的多次測量x，y坐標與其均值較差限差這一指標較為合理，可以采用表1作為內業數據處理的依據。

國外TRP外業觀測過程中并沒有實時的控制指標，這不利于觀測數據的質量控制，也不符合我國的測量習慣，應該增加各點多次測量間坐標較差這項指標，下面將探討該項指標的合理取值。

基于表4計算的估值數據，采用與表5相同的實測數據，對各點多次測量縱橫坐標差絕對值進行統計，統計結果如表6所示。

表6 實測數據多次測量坐標差絕對值統計

可見，在統計的83 364個多次測量x坐標差和y坐標差絕對值數據中：x坐標差在0.24 mm內和0.49 mm內的數據分別只占總個數的74.22%和93.96%，而在0.73 mm內和0.98 mm內的數據分別占總個數的99.18%和99.86%;y坐標差在0.24 mm內和0.49 mm內的數據分別只占總個數的73.22%和93.74%，而在0.73 mm內和0.98 mm內的數據分別占總個數的99.38%和99.84%，且相同區間的x坐標差和y坐標差統計結果基本一致。考慮到測量過程中現場環境及棱鏡安裝誤差等的影響，可采用表7所示限差指標指導TRP外業采集。

表7 各點多次測量間坐標較差限差 mm

4 主要結論

1)TRN平面網的精度評定模型彌補了國外在精度評定方面的不足，完善了TRN平面網的數據處理過程。

2)相鄰點相對點位精度定為0.2 mm偏高，現有的TRN測量方法難以達到，其合理值應為0.4 mm。

3)國外TRP各次測量坐標值與其均值較差的限差指標較合理，可以作為內業數據處理的依據，但還應增設外業測量各點多次測量間坐標較差這項控制指標。

［1］鄭健，劉成龍，楊雪峰．軌道基準網高程測量及其數據處理方法的探討［J］．鐵道建筑，2011(8)：121-124．

［2］龔辛，劉成龍，何永軍，等．高鐵軌道基準網三角高程網構網及數據處理方法研究［J］．鐵道建筑，2012(6)：118-122．

［3］武漢大學測繪學院測量平差學科組．誤差理論與測量平差基礎［M］．武漢：武漢大學出版社，2003．

［4］陳海軍，劉成龍，楊峰，等．高速鐵路軌道基準網平面網構網測量及嚴密平差方法研究［J］．鐵道科學與工程學報，2011，8(4)：55-60．

［5］中華人民共和國鐵道部．TB 10601—2009 高速鐵路工程測量規范［S］．北京：中國鐵道出版社，2009．

［6］賀挨寬．無碴軌道施工平面控制主要技術標準的研究［J］．鐵道工程學報，2006(9)：27-30．

［7］石德斌，王長進，李博峰．高速鐵路軌道控制網測量和數據處理探討［J］．鐵道工程學報，2009(4)：26-30．

U212．24;U238

A

10．3969/j．issn．1003-1995．2013．05．42

1003-1995(2013)05-0141-04

2012-07-06;

2013-02-18

西南交通大學專題研究項目(SWJTU12ZT07)

林遠胡(1988— )，男，廣東普寧人。

(責任審編 李付軍)