窄帶Rayleigh快衰落信道中改進的MMSE-SIC檢測算法

蔡 黎，代妮娜，戴閩魯，2

(1.重慶三峽學院 信息與信號處理重點實驗室，重慶404000;2.數字電視國家工程實驗室(北京)，北京101000)

責任編輯:薛 京

在無線通信系統，如CMMB(China Mobile Multimedia Broadcasting，中國移動多媒體廣播)系統中，無線信號需要在建筑物密集的城市環境中傳播，傳輸過程中信號會受到電離層和對流層反射的影響。窄帶Rayleigh快衰落信道假設信號通過無線信道之后，信號幅度隨機，即“衰落”，且其包絡服從瑞利分布，因此其通常在理論研究中被作為城市傳播環境的統計模型。

窄帶Rayleigh快衰落信道模型的廣泛應用使得針對它的無線信號檢測算法研究越來越成為熱點，常見的有ZF(Zero Forcing，迫零)、MMSE(Minimum Mean-Square Error，最小均方誤差)、ZF-SIC(Zero Forcing-Serial Interference Cancellation，迫零-串行干擾消除)和MMSE-SIC(Minimum Mean-Square Error-Serial Interference Cancellation，最小均方誤差-串行干擾消除)算法，已有文獻表明MMSE-SIC在上述算法中表現最優[1]。

實際應用中MMSE-SIC算法存在大量偽逆運算導致檢測復雜度增加[2]、惡劣情況下品質惡化情況嚴重、誤碼率較高等缺點，因此本文提出一種改進的MMSE-SIC算法。

1 常規MMSE-SIC算法

1.1 算法原理

常規MMSE-SIC算法檢測采用貝爾實驗室提出的V-Blast(Vertical-BLAST，垂直Blast)模型，模型中天線與層直接對應，即編碼后的第k個子流直接送到第k根天線，數據流與天線之間的對應關系無周期改變。因此在檢測過程中，只要知道數據來自哪根天線即可判斷其來源于哪層，檢測過程非常簡單。

設窄帶Rayleigh快衰落信道模型是空間復用MIMO系統，系統中有NR根發射天線，NT根接收天線(NR≥NT)，無線信道呈漫散射和準靜態平坦衰落，每根發射天線與接收天線之間經歷的衰落相互獨立，且接收機能夠進行理想信道估計[3]，得到MIMO系統的常規MMSE-SIC檢測模型如圖1所示。

圖1所示系統的常規MMSE-SIC檢測算法基本步驟表示如下，初始化令i=1，G1=H+(其中Gi為第i次迭代的生成矩陣，H為校驗矩陣)，而后循環執行以下矩陣迭代運算:

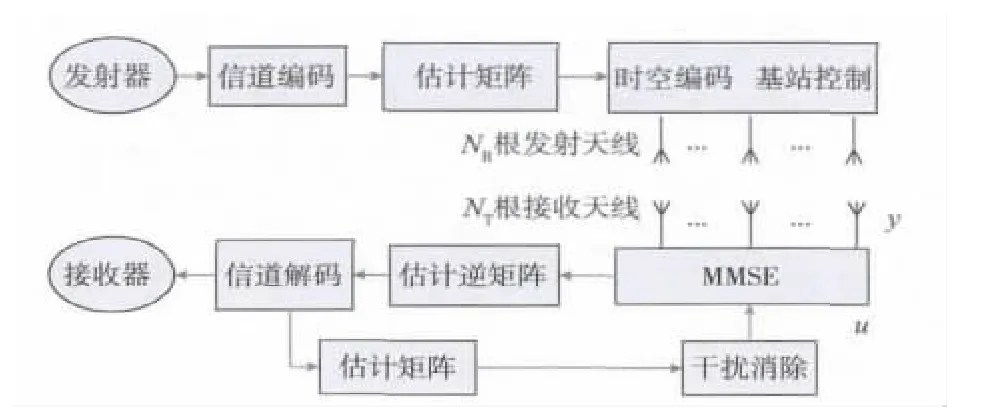
圖1 MIMO系統常規MMSE-SIC檢測模型

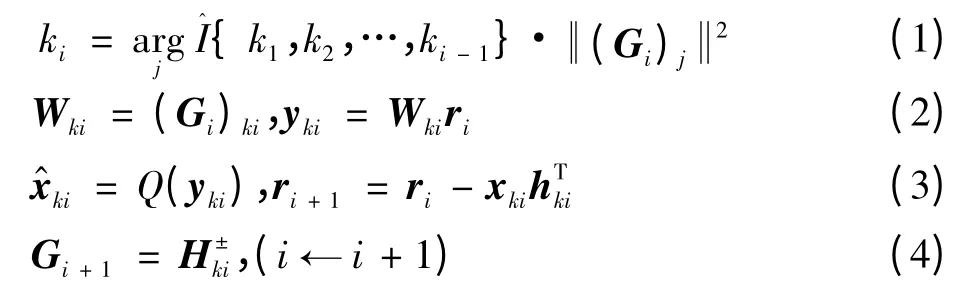
式中:ki表示第k根天線經過第i次迭代;Wki表示第ki根天線生成矩陣;yki表示第ki根天線接收到的信號;ki為經過MMSE檢測后的信號;檢測信號與校驗矩陣hki進行干擾消除得到較好的接收信號ri。

1.2 算法分析

由1.1節的MMSE-SIC原理可知，常規MMSE-SIC檢測算法是根據一定的順序依次檢測每層的發射信號，并從接收信號中消除這一層信號造成的干擾，逐次迭代，最后完成對整個信號矢量的檢測。因為后檢測的信號中干擾已經大大降低，能夠獲得較好的性能[4-5]。但是這種檢測方式需要反復進行排序和矩陣求逆操作，復雜度較高。從1.1中的迭代式可知:MMSE-SIC求解時沒有約束，直接得出檢測系數矩陣。因此算法的關鍵在于檢測時要進行反復的矩陣求逆運算。

然而在實際通信環境下，隨著通信環境惡化導致的系統參數改變，如發射、接收天線增多，信號源數據幀長增加，信噪比范圍改變等，都會增加矩陣求逆運算量，從而增加MMSE-SIC算法的復雜度和運算時間，最終降低算法的誤比特率。

2 MMSE-SIC算法的改進

2.1 核心思路

1.2 節已分析得:常規MMSE-SIC算法的最大工作量在于檢測時需要進行反復的矩陣求逆運算，因此可以思考從反復的矩陣求逆運算中尋求突破。

在此引入廣義預測控制矩陣求逆的快速算法，即在通過預測矩陣的存在改進矩陣預算的速度，從而改善整個MMSE-SIC算法的性能，改進核心思路如圖2所示。

2.2 快速矩陣和求逆算法

步驟如下:

1)構造模型

考慮如下CARIMA(Autoregressive Integrated Moving Average，差分自回歸移動平均)模型

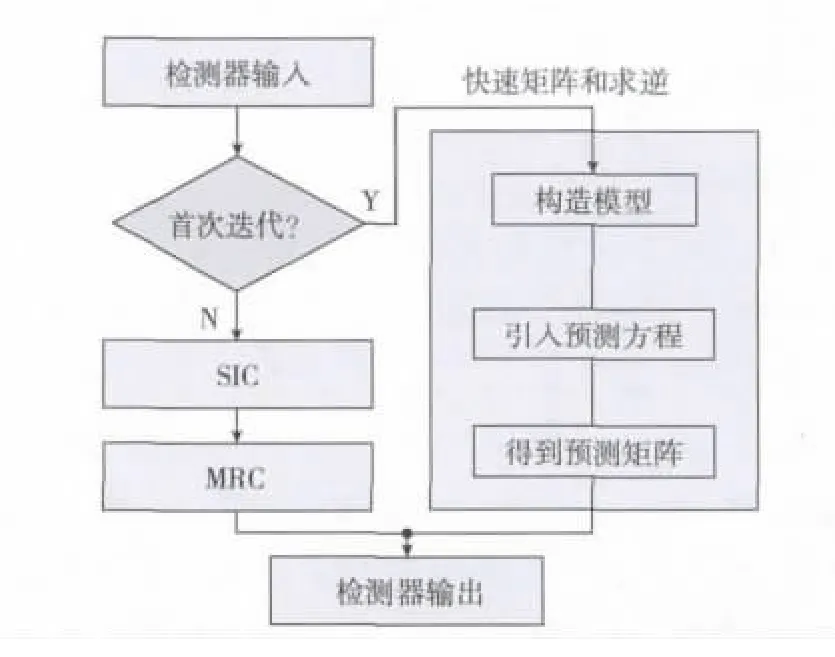
圖2 MMSE-SIC算法改進核心流程圖

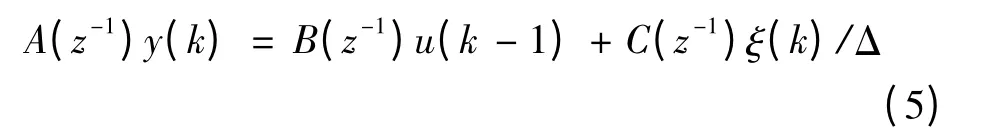
式中:y為系統輸入;u為系統輸出;ξ(k)為假設的高斯白噪聲(均值為0、方差為1);引入的差分算子Δ=1-z-1，且A(z-1)=1+a1z-1+a2z-2+…+anz-n，B(z-1)=1+b1z-1+b2z-2+…+bnz-n，C(z-1)=1+c1z-1+c2z-2+…+cnz-n。

2)引入預測方程

在CARIMA模型中引入Diophantine方程以實現預測，方程中包含由A(z-1)、B(z-1)唯一確定的多項式，預測長度j，Diophantine方程[6]為

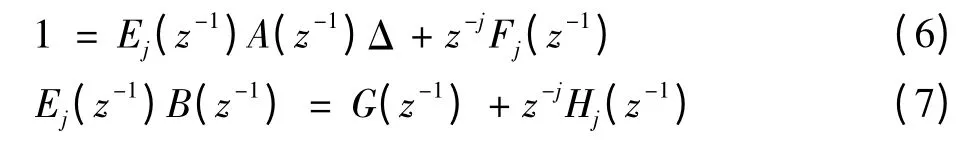
3)得到預測矩陣

令N為預測時域，Nu為控制時域(Nu＜N)，得到系統輸出預測矩陣為

U=[Δu(k)，Δu(k+1)，…，Δu(k+Nu-1)]T;F=[F1(z-1)，F2(z-1)，…，FN(z-1)]T;H=[H1(z-1)，H2(z-1)，…，HN(z-1)]T;E=[E1(z-1)ξ(k+1)，E2(z-1)ξ(k+2)，…，EN(z-1)ξ(k+N)]T;G的表達式為

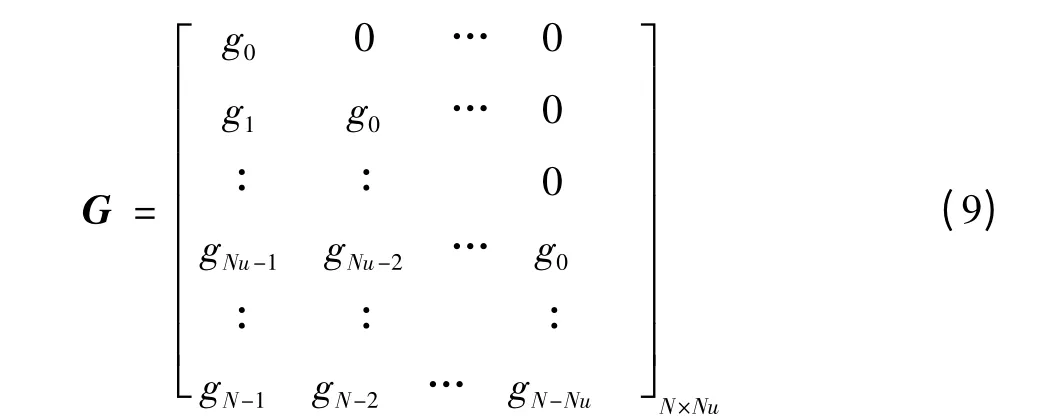
至此，快速矩陣和求逆算法即得。

3 仿真與分析

3.1 仿真結果

選MATLAB7.0為仿真環境，以第2.2節中提出的改進MMSE-SIC算法為仿真對象，傳統ZF、ZF-SIC、MMSESIC作為對比仿真對象，設信源A是幀長為2 000的比特流，經BPSK(Binary Phase Shift Keying，二進制相移鍵控)調制后發射，引入一定強度的高斯白噪聲，用M文件建立窄帶Rayleigh快衰落信道通信模型[7]，構造4種不同的通信環境，以觀察不同通信環境下不同檢測算法的誤比特率表現。

4種通信環境:1)理想通信環境:發射天線數4、接收天線數3，信噪比范圍0～20 dB;2)普通通信環境:發射天線數2、接收天線數2，信噪比范圍0～20 dB;3)惡劣通信環境:發射天線數2、接收天線數2，信噪比范圍0～20 dB;4)極端通信環境發射天線數2、接收天線數2，信噪比范圍0～20 dB。

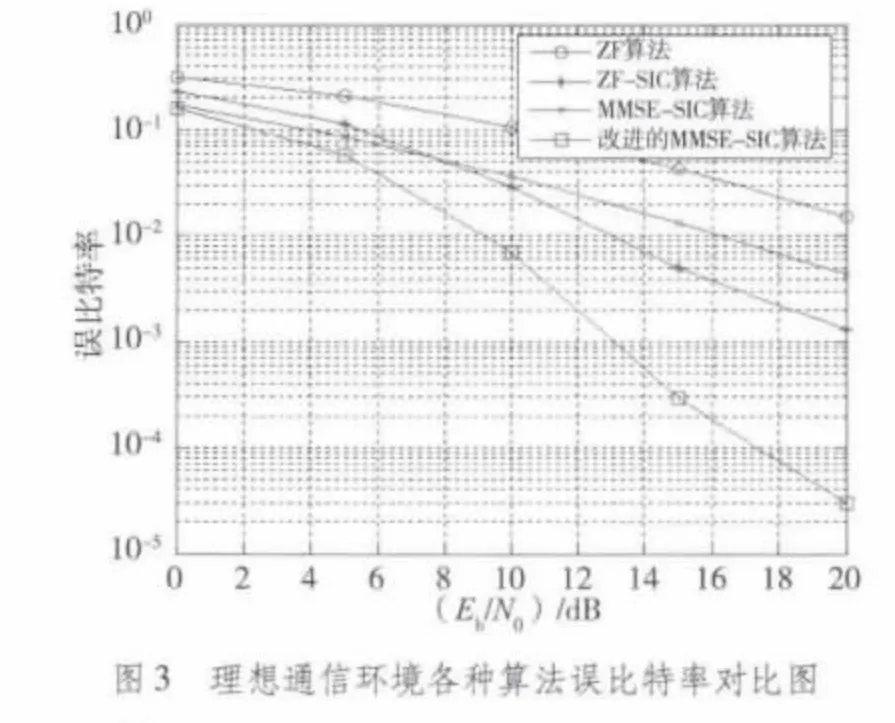
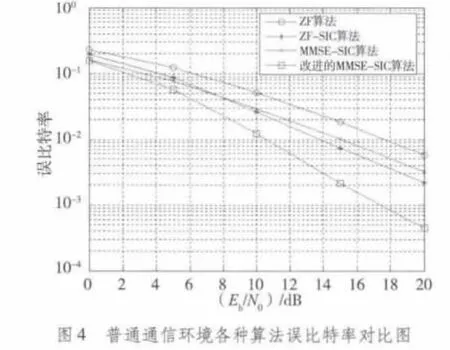
以足夠多的數據進行運算，得到仿真結果如圖3～圖6所示。

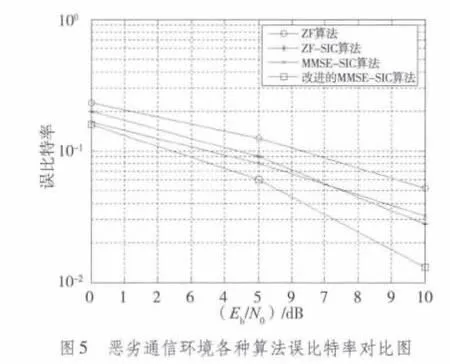
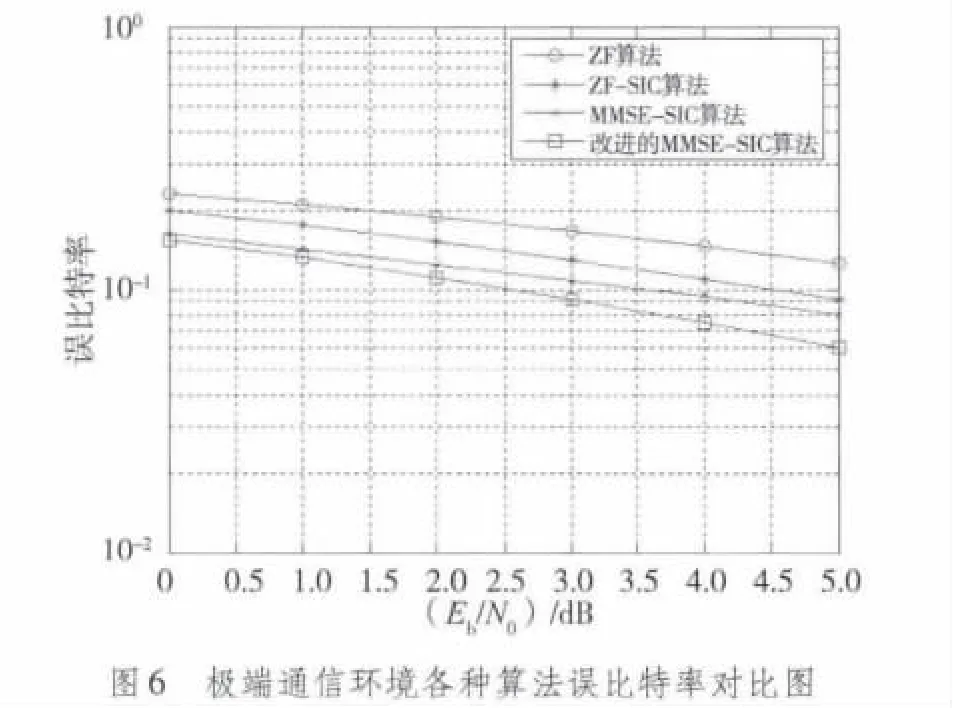
3.2 結果分析

從仿真結果圖可知，在理想通信環境下，4種算法均有較好的誤比特率表現，理想通信環境下4種算法誤比特率表現都很好，但改進后的MMSE-SIC的表現最優，誤比特率逼近10-4數量級;普通通信環境下，4種算法也均呈較好的誤比特率表現，改進后的MMSE-SIC的表現最優，誤比特率逼近10-4的數量級;在惡劣通信環境下，4種算法通信品質呈一定惡化，改進后的MMSE-SIC的表現仍然最優，誤比特率接近10-2數量級;在極端通信環境下，4種算法通信品質都嚴重惡化，誤碼率均徘徊在10-1的數量級上下，改進后的MMSE-SIC的表現仍然相對最優。

4 小結

本文通過引入預測矩陣改善矩陣運算的速度，從而改善了常規MMSE-SIC檢測算法的性能，仿真表明改進的MMSE-SIC算法相對于常規MMSE-SIC算法，在各種通信環境下均表現出了較好的誤比特率性能，具有較高的參考和應用價值。

[1]黃玉娟.VBLAST系統的譯碼算法研究[J].通信技術，2011(2):65-68.

[2]張建忠.基于QR分解的V-BLAST檢測算法研究[J].電視技術，2010，34(5):89-91.

[3]范忠亮.基于矩陣和求逆及MRC的低復雜度MIMO檢測器[J].測控技術，2011(9):98-101.

[4]包亞偉.一種新的高效MMSE-SIC檢測算法[J].系統仿真學報，2011(7):1350-1353.

[5]CHEN Jiming，JIN Shan，WANG Yonggang.Reduced complexity MMSESIC detector in V-BLAST systems[C]//Proc.18th Annual IEEE International Symposium on Personal，Indoor and Mobile Radio Communications.Athens:IEEE Press，2007:1-5.

[6]陳志興.廣義預測控制矩陣求逆的快速算法研究[J].科技信息，2012(31):89-90.

[7]邱佳新.V-BLAST程序[EB/OL].[2013-01-10].http://www.pudn.com/downloads254/sourcecode/math/detail1175182.html.