一種新型delta-sigma小數(shù)分頻器的FPGA實(shí)現(xiàn)
王水魚(yú),馮曉靖
(西安理工大學(xué) 自動(dòng)化與信息工程學(xué)院,陜西 西安 710048)
新一代移動(dòng)通信系統(tǒng)對(duì)頻率源的要求集中在低相位噪聲、快捷變這兩個(gè)方面[1]。delta-sigma調(diào)制(DSM)技術(shù)最初應(yīng)用于模數(shù)轉(zhuǎn)換[2-5],但其良好的噪聲成型技術(shù)卻使其應(yīng)用相當(dāng)廣泛,一個(gè)最典型的例子就是應(yīng)用于小數(shù)分頻技術(shù)[6-8]。眾所周知,經(jīng)典小數(shù)分頻的一個(gè)最大的瓶頸就是其輸出相位噪聲比較嚴(yán)重[9]。而相噪指標(biāo)太低,必然制約了小數(shù)分頻技術(shù)在當(dāng)今無(wú)線(xiàn)通信系統(tǒng)中的應(yīng)用[10-12]。DSM在小數(shù)-N頻率合成方面的應(yīng)用主要起到一個(gè)調(diào)節(jié)分頻比的作用。輸入一個(gè)常數(shù),這個(gè)常數(shù)為小數(shù)-N分頻的分?jǐn)?shù)部分值,輸出為不斷變化的分頻比,利用DSM噪聲成型的作用,量化部分的噪聲可以被DSM本身搬移到高頻的部分,這樣,就可以利用PLL本身的低通性能,在噪聲加到VCO之前就被濾除掉。因此,DSM技術(shù)既可以實(shí)現(xiàn)小數(shù)分頻,同時(shí)又可以較好地抑制小數(shù)分頻出現(xiàn)的雜散情況。
1 delta-sigma原理分析
delta-sigma(△-∑)調(diào)制具有噪聲整形特性,能將噪聲從低頻段整形到高頻段,大大減小了帶寬內(nèi)的量化噪聲[13]。單環(huán)的delta-sigma調(diào)制器實(shí)質(zhì)是一個(gè)單階誤差反饋電路,其結(jié)構(gòu)如圖1所示。
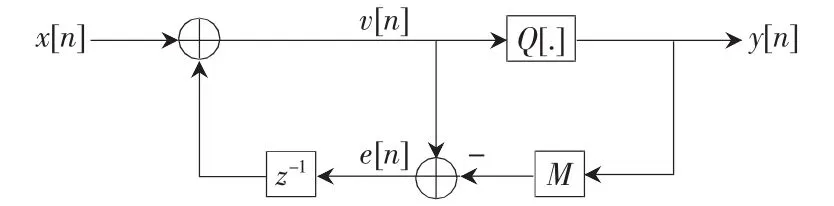
圖1 單環(huán)delta-sigma調(diào)制器
其中,x[n]為 n bit表示的小數(shù)分頻比,Q[.]為量化器,y[n]為量化輸出,M滿(mǎn)足 M=2n。該結(jié)構(gòu)與一級(jí)相位累加器的數(shù)學(xué)模型是一致的,因此可以用一級(jí)累加器來(lái)實(shí)現(xiàn)單環(huán)△-∑調(diào)制器,累加器模型如圖2所示。
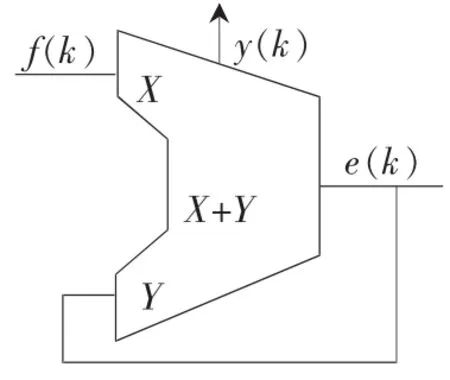
圖2 一級(jí)累加器模型
令累加器位數(shù)為 n bit,同理,f(k)表示分頻比的小數(shù)部分,y(k)為累加器溢出值,溢出為1,否則為0,e(k)為累加值。 一級(jí)相位累加器作為單環(huán) △-∑調(diào)制器對(duì)其自身量化誤差e(k)具有一定的濾波作用,但十分有限,通常會(huì)采用高階MASH結(jié)構(gòu)以克服量化誤差。
MASH1-2-1結(jié)構(gòu)是在三級(jí)MASH結(jié)構(gòu)的基礎(chǔ)上加以改進(jìn)的結(jié)構(gòu),量化器產(chǎn)生的白噪聲經(jīng)過(guò)幾級(jí)調(diào)制后就被變換成了高通型噪聲,噪聲能量絕大部分處于鎖相環(huán)本身的低通濾波通帶之外。該結(jié)構(gòu)包含了兩個(gè)一階量化器和一個(gè)二階量化器,一階量化器的結(jié)構(gòu)如圖1所示,二階量化器結(jié)構(gòu)如圖3所示。
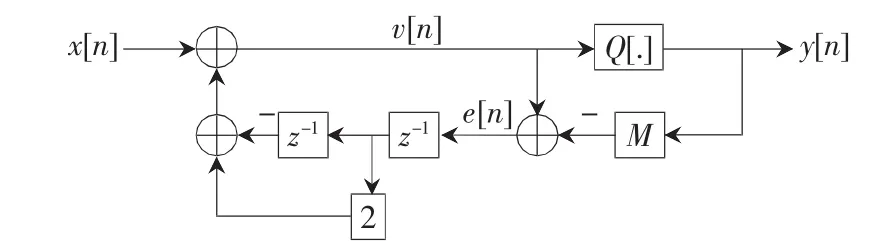
圖3 二階△-∑誤差反饋結(jié)構(gòu)
該結(jié)構(gòu)的Z域模型為:
Y(z)=X(z)-(1-H(z))E(z)
其中,H(z)=1-(1-z-1)2=2z-1-z-2。
噪聲傳遞函數(shù)為:
N(z)=(1-z-1)2
MASH1-2-1結(jié)構(gòu)如圖4所示。
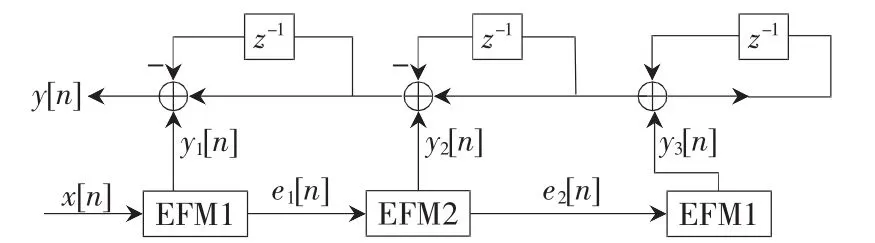
圖4 MASH1-2-1結(jié)構(gòu)框圖
由圖 4 可知,輸入輸出關(guān)系為 Y(z)=X(z)-(1-z-1)4E3(z),且噪聲傳遞函數(shù)為 N(z)=(1-z-1)4。 由于第三級(jí)誤差反饋結(jié)構(gòu)的誤差輸出序列的周期很長(zhǎng),可以近似視為隨機(jī)序列,將此信號(hào)序列反饋回輸入端,相當(dāng)于在輸入端注入了抖動(dòng)信號(hào),可以進(jìn)一步降低雜散信號(hào)的周期性,減少雜散信號(hào)離散譜線(xiàn)的輸出。加入抖動(dòng)信號(hào)的MASH1-2-1結(jié)構(gòu)如圖5所示。
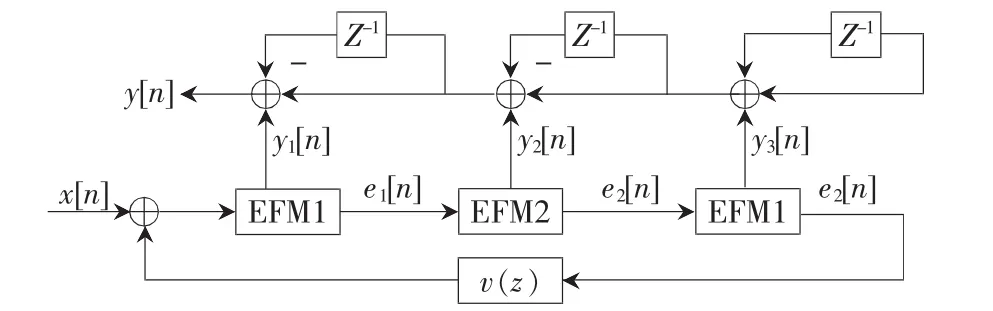
圖5 加入抖動(dòng)的MASH1-2-1結(jié)構(gòu)
其中,v(z)是為了降低輸入噪聲而設(shè)置的二階濾波器,v(z)=(1-z-1)2。
2 基于delta-sigma小數(shù)分頻的FPGA實(shí)現(xiàn)
小數(shù)N分頻器是通過(guò)周期性地改變分頻比使平均分頻比為N+F/M,其中,F(xiàn)為數(shù)字量化后的分頻比小數(shù)部分,M為n比特累加器的最大值2n。小數(shù)分頻器的輸入輸出頻率關(guān)系為fvco=N.F×fREF,其小數(shù)分頻鎖相環(huán)結(jié)構(gòu)方框圖如圖6所示。
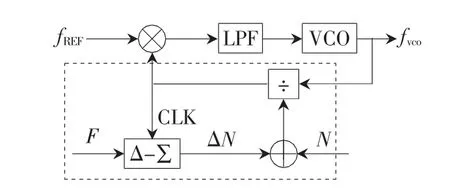
圖6 delta-sigma結(jié)構(gòu)的小數(shù)分頻鎖相環(huán)
圖6中虛線(xiàn)框內(nèi)的結(jié)構(gòu)即為需用FPGA實(shí)現(xiàn)的delta-sigma小數(shù)分頻部分,該部分可分為delta-sigma調(diào)制模塊和整數(shù)分頻模塊兩個(gè)模塊設(shè)計(jì)。△-∑調(diào)制模塊采用小數(shù)分頻后的時(shí)鐘信號(hào)作為參考信號(hào),根據(jù)小數(shù)分頻值F來(lái)產(chǎn)生周期性可變分頻比 △N,使得N+△N的均值為N.F,整數(shù)分頻器根據(jù)分頻比N+△N對(duì)VCO輸出的信號(hào)進(jìn)行分頻,并將分頻后的信號(hào)送往鑒相器與參考信號(hào)進(jìn)行比較。下面分別討論delta-sigma調(diào)制部分和整數(shù)分頻部分的FPGA實(shí)現(xiàn)。
delta-sigma調(diào)制部分采用圖5所示的加入抖動(dòng)的MASH1-2-1結(jié)構(gòu),EFM1可以直接利用一階累加器實(shí)現(xiàn),EFM2可以采用一階加法器和D觸發(fā)器來(lái)組合構(gòu)成,同樣v(z)也可利用一系列D觸發(fā)器組合實(shí)現(xiàn)。由于要對(duì)EFM1和EMF2的溢出值進(jìn)行加減運(yùn)算,因此需將溢出值轉(zhuǎn)換為補(bǔ)碼表示,且加法器需進(jìn)行補(bǔ)碼的加減運(yùn)算。對(duì)于MASH1-2-1結(jié)構(gòu)來(lái)說(shuō),最終輸出的由小數(shù)分頻比產(chǎn)生的控制信號(hào) △N可能存在的值為±3,±2,±1,0。再利用加法器將整數(shù)分頻比輸入N和控制分頻比△N相加,就得到控制鎖相環(huán)整數(shù)分頻比變化的分頻信號(hào)。MASH1-2-1結(jié)構(gòu)的頂層原理圖如圖7所示。
3 實(shí)驗(yàn)結(jié)果與分析
該頂層原理圖通過(guò)仿真得到輸出分頻比的仿真波形如圖8所示。f_N為輸入的整數(shù)分頻比,frac是輸入的小數(shù)分頻比部分,由于累加器采用8 bit位寬,故此時(shí)真正的小數(shù)分頻比為 F=93/256≈0.4,fdiv_N即為輸出的實(shí)際整數(shù)分頻比N+△N,其均值應(yīng)為N.F=10.36。
整數(shù)分頻器根據(jù)delta-sigma調(diào)制器輸出的分頻比對(duì)VCO的輸出信號(hào)進(jìn)行分頻,在完成一次分頻過(guò)程后再?gòu)膁elta-sigma調(diào)制器中取下一個(gè)分頻比進(jìn)行下一次分頻。由于分頻比可能為奇數(shù)也可能為偶數(shù),故分頻器必須能夠?qū)崿F(xiàn)奇數(shù)分頻和偶數(shù)分頻。
分頻器仿真波形如圖9所示。
圖9中,freq_in為輸入的待分頻信號(hào),div_N是輸入的整數(shù)分頻比,可以看出,該分頻器既能實(shí)現(xiàn)奇數(shù)分頻又能實(shí)現(xiàn)偶數(shù)分頻,且當(dāng)分頻比改變時(shí),能夠及時(shí)地根據(jù)新分頻比進(jìn)行分頻。
綜合以上分析即可得到delta-sigma小數(shù)分頻器,如圖10所示,freq_out就是小數(shù)分頻后的輸出信號(hào)。
所得到的仿真波形如圖11所示。從圖11可以看出,freq_out是分頻比為10.4的仿真波形。在對(duì)應(yīng)的整數(shù)分頻比內(nèi),輸出信號(hào)正確地按照該分頻比值fdiv_N進(jìn)行分頻;輸入分頻比變化時(shí),輸出信號(hào)頻率也能及時(shí)地發(fā)生相應(yīng)變化,從而實(shí)現(xiàn)了對(duì)輸入信號(hào)的小數(shù)分頻。
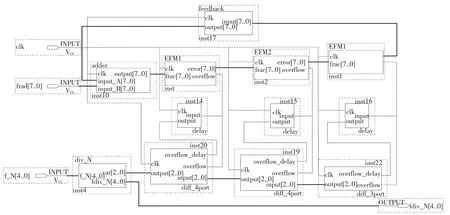
圖7 MASH1-2-1結(jié)構(gòu)頂層原理圖

圖8 delta-sigma調(diào)制輸出分頻比
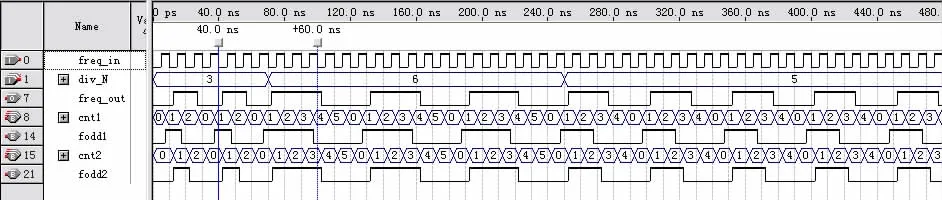
圖9 分頻器輸出波形
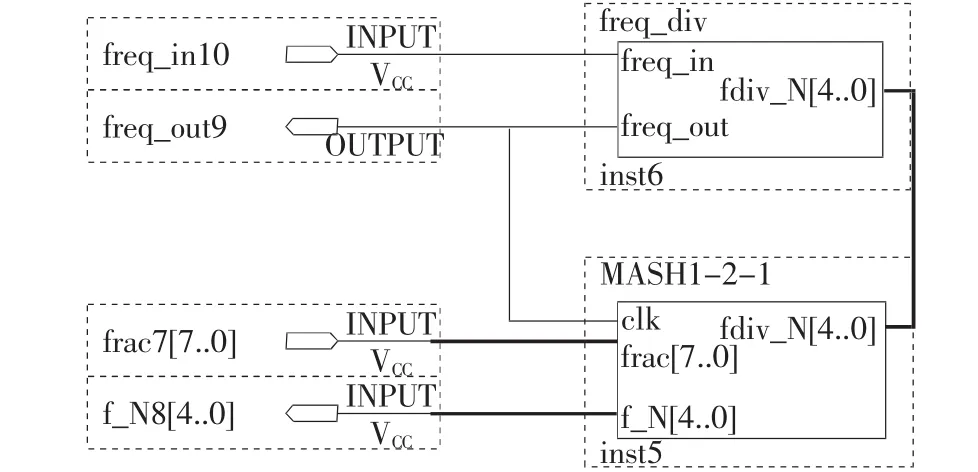
圖10 △-∑小數(shù)分頻器

圖11 △-∑小數(shù)分頻仿真結(jié)果
本文通過(guò)對(duì)MASH1-2-1結(jié)構(gòu)原理的分析,論述了可實(shí)現(xiàn)的FPGA模型,并完成了基于FPGA的deltasigma小數(shù)分頻器的實(shí)現(xiàn)。該結(jié)構(gòu)不用于一般的MASH單階多級(jí)結(jié)構(gòu),在第二級(jí)引入二級(jí)誤差反饋環(huán)路,使得調(diào)制器整體階數(shù)為四階,這樣做的目的在于:在不增加MASH結(jié)構(gòu)級(jí)數(shù)的情況下,通過(guò)改變單元調(diào)制器的結(jié)構(gòu)來(lái)降低量化噪聲。同時(shí),為了使得輸出噪聲功率譜曲線(xiàn)更加平滑,在輸入端引入隨機(jī)序列來(lái)打斷輸出周期性。通過(guò)FPGA實(shí)現(xiàn)模塊化,可以很方便地嵌入到鎖相環(huán)的設(shè)計(jì)中,提高了設(shè)計(jì)的通用化和高效化。
[1]RILEY T A D,COPELAND M A, KWASNIEWKI T A.Delta-sigma modulation in fractional-N frequency synthesis[J].IEEE Journal of Solid-State Circuit, 1993,28(5):553-559.
[2]REINHARDT V, GOULD K, MCNAB K, et al.A short survey of frequency synthesiser techniques[C].40th Annual Symposium on Frequency Control,1986:355-365.
[3]WARE K M,LEE H,SODINI C G.A 200 MHz CMOS phase-locked loop with dual phase detectors[C].1989 IEEE InternationlSolid-State Circuits Conference,36th ISSCC,Digest of Technical Papers, 1989:192-193.
[4]CANDY J C,BENJAMIN O.The structure of quantization noise from sigma delta modulation[J].IEEE Transactions on Communications,1981,29(9):1316-1323.
[5]CANDY J C.Use of double integration in sigmadelta modulation[J].IEEE Transactions on Communications,1985,33(3):249-258,.
[6]NORSWORTHY S R, SCHREIER R,TAMES G C.Deltasigma data converters[M].New York: Wliey IEEE Press,1997.
[7]MOTAMED M,SANDERS S,ZAKHOR A.The double loop sigma delta modulator with unstable filter dynamics:stability analysis and tone behavior[J].IEEE Transactions on Circuits and Systems II: Anglog and DigitalSignalProcessing,1996,43(8):549–559.
[8]KOZAK M A,KALE I.A pipelined noise shaping coder for fractional-N frequency synthesis[J].IEEE Transactions on Instrumentation and Measurement, 2001,50(5):1154-1161.
[9]MENINGER S E,PERROTT M H.A fractional-N frequency synthesizer architecture utilizing a mismatch compensated PFD/DAC structure for reduced quantizationinduced phase noise[J].IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, 2003,50(11):839-849.
[10]PAMARTI S,GALTON I.LSB dithering in MASH deltasigma D/A converters[J].IEEE Transactions on Circuits and Systems I: Regular Papers, 2007,54(4):779-790.
[11]KOZAK M,KALE I.Rigorous analysis of delta-sigma modulatorforfractional-N PLL frequency synthesis[J].IEEE Transactions on Circuits and Systems I: Regular Papers, 2004,51(6):1148-1162.
[12]MILLER B,CONLEY R J.A multiple modulator fractional divider [J].IEEE Transactions on Instrumentation and Measurement, 1991,40(3):576–583.
[13]BORKOWSKI M J, RILEY T A D, HAKKINEN J, et al.A practical△-∑ modulatordesign method based on periodicalbehavior analysis [J].IEEE Transactions on Circuits and Systems II: Express Briefs,2005,52(10):626-630.

