級配碎石動三軸試驗的數值模擬方法

蔣應軍 李思超 王天林

(1 長安大學特殊地區公路工程教育部重點實驗室，西安710064)

(2 陜西省交通建設集團，西安710075)

路基路面承受車輛荷載動態作用，而道路材料的動態特性直接影響路面耐久性［1］.國內外對道路材料動態特性做了一些研究.如Gaskin 等［2］探討了Sydenham 砂在反復荷載下的行為，指出其破壞的類型屬永久變形破壞，破壞發生的時機是應變率增大至最大時.Werkmeister 等［3－4］針對2 類粒狀土進行了不同軸差應力及圍壓下的三軸反復荷載試驗，發現粒狀土在反復荷載過程中具有安定行為.何兆益［5］采用動三軸試驗對比研究了不同級配的級配碎石動態特性，并給出了建議級配及其成型方法.廖化榮［6］結合安定理論和能量耗散觀點，采用動三軸試驗確定了不同含水量紅黏土在循環荷載作用下的臨界應力水準及其破壞包絡線.王龍等［7］研究了級配碎石基層在長期車輛荷載作用下塑性變形的發展規律和分布狀態.

級配碎石常用于道路路面基層，研究其動態特性對于提高路面耐久性具有重要意義［1］.目前，常用室內動三軸試驗研究道路材料的動態特性.但道路材料動態特性影響因素較多，而室內動三軸試驗效率低、成本高，因此采用室內動三軸試驗研究道路材料動態特性，其研究深度和廣度受限.

鑒于此，本文基于PFC2D提出了級配碎石動三軸數值模擬方法(numerical simulation method of dynamic triaxial test，DTT－NSM)，該方法是對室內動三軸試驗的補充，為深入研究級配碎石動態特性提供了新的思路，同時也為其他道路材料動態特性研究提供借鑒.

1 級配碎石DTT－NSM 的構建

1.1 PFC2D軟件的簡介

PFC2D軟件是由ITASCA 咨詢集團開發的顆粒流分析程序，屬于離散單元方法.它主要通過圓形離散單元來模擬顆粒介質的運動及其相互作用關系，利用接觸本構關系描述顆粒的受力狀態，采用牛頓第二定律建立運動方程，以動態松弛法迭代求解，獲得材料整體的運動形態與宏觀力學性能.PFC2D的計算過程如下:①接觸檢索;②利用接觸本構關系計算作用于顆粒上的不平衡力與不平衡力矩;③計算顆粒的運動參數(運動參數滿足牛頓第二定律);④更新顆粒位置，進行下一步迭代.PFC2D能從細觀角度深化研究固結和松散介質材料的裂紋擴展、破壞累積、斷裂、破壞沖擊和微震響應等力學行為.

1.2 構建思路

級配碎石動態特性受集料物理特性、礦料級配、試件成型方式、試驗條件等因素影響，本文采用顆粒流數值模擬技術，通過構建虛擬試件、模擬力學試驗、反演獲取微力學參數等來表征這些影響因素，確保提出的級配碎石DTT－NSM 所獲得的模擬結果的可靠性.級配碎石DTT－NSM 構建思路如圖1所示.

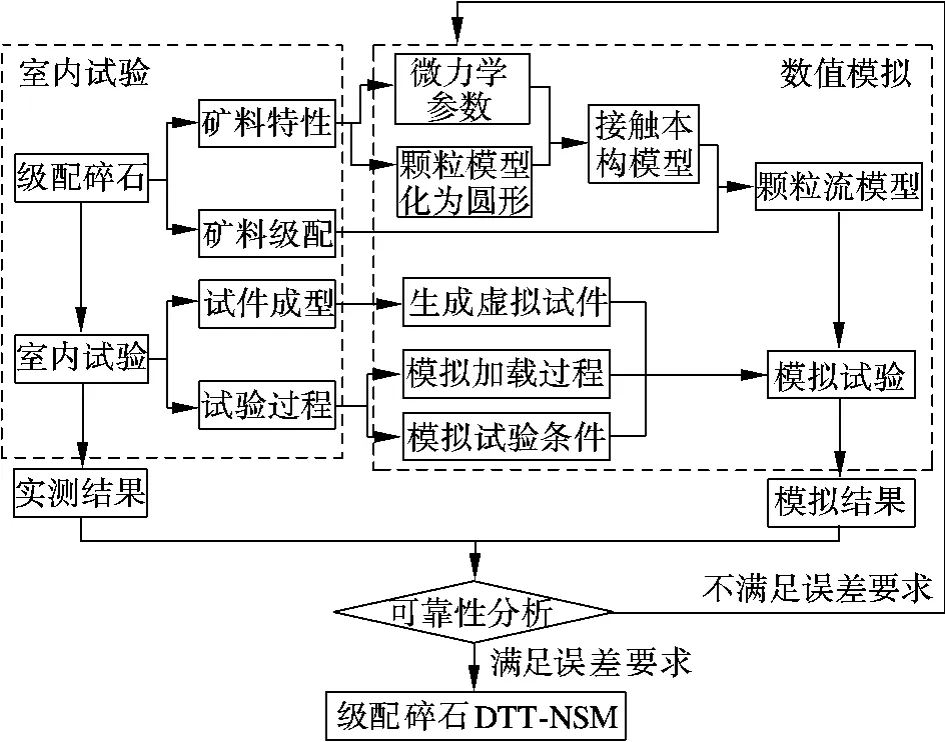
圖1 級配碎石DTT-NSM 構建思路

級配碎石DTT－NSM 接觸本構模型選用線性接觸剛度模型.該模型是通過2 個接觸實體(球－球或者球－邊界墻)間的法向剛度kn、切向剛度ks和摩擦系數μ 定義的.kn反映了顆粒表面接觸狀態，ks反映了集料顆粒彈性模量，μ 反映了集料表面粗糙程度及相互接觸狀況、含水率等.

1.3 物理模型的構建

物理模型的構建步驟如下:

①試模的模擬.采用以四面墻體形成的封閉矩形試模.

②級配碎石的生成.在試模內生成集料顆粒，通過監測生成顆粒的面積控制每種規格集料的用量，以達到目標級配.

③壓頭的生成.在頂面、底面墻體兩側位置生成一排球體模擬級配碎石動三軸試驗壓頭，同時將兩面墻體沿水平方向抽出，使模擬壓頭集料直接接觸，如圖2所示.

圖2 級配碎石DTT-NSM 模型

1.4 模擬試驗條件的實現

模擬試驗條件的實現方法如下:

1)圍壓.利用伺服機制控制墻體速度以保持墻體和顆粒之間的應力恒定，實現圍壓的控制.

2)穩壓.對兩側墻體施加圍壓σ3，對模擬壓頭施加靜荷載σs，以保證當動載作用時不產生沖擊應力，當靜荷載作用下試樣變形基本穩定后，穩壓過程結束.

3)動載.模擬激振設備對試樣施加循環荷載，采用室內試驗常用的正弦波，偏應力σd=σ1－σ3=σd0sinwt，其中σ1為軸向應力，w 為簡諧應力的圓頻率.每次施加荷載時間包括動載作用時間tz和動載作用間隔時間tj，其中tz包括加載時間和卸載時間.

1.5 加載方式的確定

為了說明加載方式、試件尺寸和微力學參數對模擬結果的影響，后續研究以文獻［8］為例，原材料為石灰巖碎石，其級配見表1.微力學參數標定結果見表2.

表1 礦料級配

表2 微力學參數

1.5.1 荷載大小和作用次數

級配碎石軸向應變ε 和動載作用次數N 關系見圖3，級配碎石動載作用1 000 次下軸向應變ε1000和偏應力σd關系見圖4.試件尺寸取直徑φ=20 cm，高度h =40 cm，動載作用時間tz和作用間隔時間tj分別取0.2 s 和2.0 s.

圖3 不同偏應力下軸向應變和動載作用次數曲線

由圖3可知，當N≤1 000 次時，ε 隨N 增加而急劇增大.當N ＞1 000 次，ε 隨N 呈近似線性增加，且動載越大，ε 增加幅度也越大.同時，模擬試件在1 000 次動載作用下，塑性變形已趨于穩定.因此，為了簡化試驗，本文動載作用次數取1 000 次.

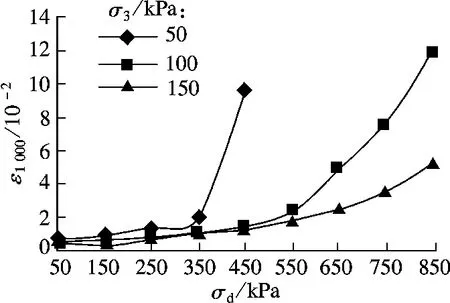
圖4 動載作用1 000 次下軸向應變和偏應力曲線

由圖4可知，在不同圍壓σ3下，偏應力σd對軸向應變影響規律相似.隨著σd增大，ε1000先緩慢增大，當σd＞450 kPa(σ3=100～150 kPa)或σd＞350 kPa(σ3=50 kPa)時急劇增大，此值稱為失穩偏壓.級配碎石失穩偏壓隨圍壓增大而增大，說明提高圍壓能提高級配碎石抗變形能力.荷載響應分析表明，級配碎石過渡層偏應力水平一般為150～350 kPa［9］.結合圖3，當σd≤350 kPa 時，3 種圍壓下級配碎石ε 與σd接近成線性關系.因此，若無特殊說明，下文研究中應力水平取σ3=50 kPa，σd=250 kPa.

1.5.2 加載方式

動載作用時間tz和動載作用間隔時間tj與動載作用1 000 次下軸向應變ε1000的關系見圖5.

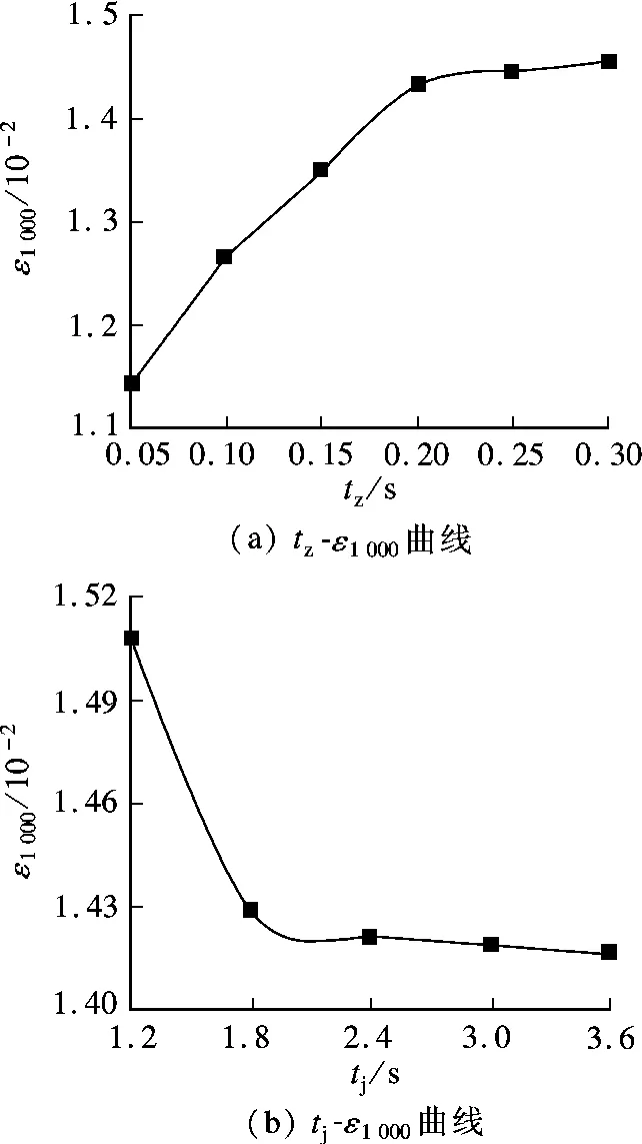
圖5 加載方式對級配碎石ε1 000影響曲線

由圖5(a)可知，隨著動載作用時間從0.05 s增大到0.2 s，級配碎石ε1000基本呈線性增長規律，當動載作用時間大于0.2 s，ε1000變化趨于平緩，此時，繼續增大動載作用時間對試驗結果影響不大.由圖5(b)可知，當tj≤2.0 s 時，ε1000隨作用間隔時間的增大而明顯減小，當tj≥2.0 s 時，ε1000隨tj的增大而變化不大，此時，繼續增大動載作用間隔時間對試驗結果影響不大.

動載加載方式的確定應考慮車輛荷載實際情況.對于高等級公路，行車速度為80～120 km/h，動載作用時間約為0.05～0.08 s，動載作用間隔時間一般為3.6 s，同時考慮動載加載方式對級配碎石ε1000影響曲線，按不利情況選取，建議動載作用時間和動載作用間隔時間分別取0.2 s 和2.0 s.

1.6 試件尺寸的確定

1.6.1 試件高度

級配碎石動載作用1 000 次下軸向應變ε1000隨試件高度h 變化規律見圖6.試件直徑φ =20 cm，Dmax為集料公稱最大粒徑.

圖6 動載作用1 000 次下軸向應變和試件高度曲線

由圖6可知，不同Dmax的級配碎石試件高度h對ε1000影響規律相似.隨著試件高度增大，ε1000先減少，后趨于穩定.當Dmax≤37.5 mm 時，ε1000趨于穩定時的試件h≥40 cm;當Dmax=53 mm 時，ε1000趨于穩定時的試件h=30 cm.因此，試件h≥40 cm時，碎石粒徑對試驗結果影響趨于穩定.

1.6.2 試件直徑

級配碎石動載作用1 000 次下軸向應變ε1000隨試件直徑φ 的變化規律見圖7.試件h=40 cm.

由圖7可知，不同Dmax的級配碎石試件直徑φ對ε1000影響規律相似，隨著試件直徑φ 增大，ε1000先減少，后趨于穩定.當公稱最大粒徑Dmax≥26.5 mm 時，ε1000趨于穩定時的試件直徑φ≥20 cm;當公稱最大粒徑Dmax≤26.5 mm 時，ε1000趨于穩定時的試件直徑φ≥15 cm.因此，試件直徑φ≥20 cm時，碎石粒徑對試驗結果影響趨于穩定.

圖7 動載作用1 000 次下軸向應變和試件直徑曲線

綜上，為了減小碎石粒徑對試驗結果的影響，同時兼顧數值試驗仿真度和計算速度，建議試件尺寸取φ20 cm ×40 cm.

1.7 級配碎石DTT－NSM 的可靠性驗證

以文獻［8］為例，對級配碎石DTT－NSM 的可靠性進行了驗證，結果見圖8.

圖8 模擬結果與室內試驗結果對比

由圖8可知，級配碎石ε 和動載作用次數N關系模擬結果和實測結果基本吻合，證明級配碎石動三軸數值試驗方法是可靠的.

2 微力學參數的敏感性及其標定方法

級配碎石微力學參數無法實測，只能通過室內試驗結果進行標定.本文通過研究微力學參數對模擬結果的影響規律進行微力學參數標定.

2.1 微力學參數的敏感性

2.1.1 法向剛度kn

不同法向剛度kn下，級配碎石軸向應變ε 和動載作用次數N 關系見圖9.動載作用1 000 次下軸向應變ε1000和法向剛度kn關系見圖10.計算時，取切向剛度ks=10 GPa，摩擦系數μ=0.5.

由圖9可知，不同法向剛度kn下，級配碎石ε隨N 變化曲線形態相似.由圖10可知，隨法向剛度kn增大，ε1000近似于線性減小，但ε1000值減小幅度有限.法向剛度kn每增加1 GPa，本文研究的級配碎石ε1000約減小0.3%.

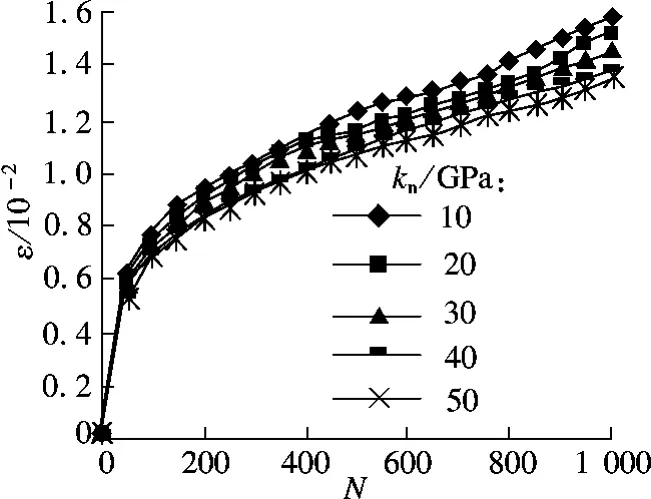
圖9 不同法向剛度下軸向應變和動載作用次數曲線

圖10 動載作用1 000 次下軸向應變和法向剛度曲線

2.1.2 切向剛度ks

不同切向剛度ks下，級配碎石ε 和動載作用次數N 關系見圖11.動載作用1 000 次下軸向應變ε1000和切向剛度ks關系見圖12.計算時，取法向剛度kn=10 GPa，摩擦系數μ=0.5.

圖11 不同切向剛度下軸向應變和動載作用次數曲線

圖12 動載作用1 000 次下軸向應變和切向剛度曲線

由圖11可知，不同切向剛度ks下，級配碎石ε隨N 變化曲線形態相似.由圖12可知，隨切向剛度ks增大，ε1000近似于線性減小，但ε1000值減小幅度有限.切向剛度ks每增加1 GPa，本文研究的級配碎石ε1000約減小0.8%.

2.1.3 摩擦系數μ

不同摩擦系數μ 下，級配碎石軸向應變ε 和動載作用次數N 關系見圖13.動載作用1 000 次下軸向應變ε1000和摩擦系數μ 關系見圖14.計算時，取kn=ks=10 GPa.

圖13 不同摩擦系數下軸向應變和動載作用次數曲線

圖14 動載作用1 000 次下軸向應變和摩擦系數曲線

由圖13可知，當摩擦系數μ ＜0.5 時，級配碎石ε 隨N 增加持續增大，這與實際情況差異較大.當摩擦系數μ≥0.5 時，振次達到100 次后，軸向應變ε 增大趨勢開始減弱，之前的不利情況得到緩解.由圖14可知，隨摩擦系數μ 增大，ε1000近似于線性減小.摩擦系數μ 每增加0.1，本文研究的級配碎石ε1000約減小16%.

因此，建議摩擦系數μ 取值在0.5～1.0 之間，取初值后，根據級配碎石含水率適當調整.

2.2 微力學參數標定方法

微力學參數不僅反映試驗條件、集料特性和含水量等因素對力學性能的影響，而且也是對各種假設的一種綜合修正［10－11］.本文采用的微力學參數標定方法的具體過程如下:

①通過室內試驗獲取2～3 組不同級配級配碎石DTT 軸向應變的實測值.

②根據原材料及級配，構建級配碎石DTT 數值模型，對微力學參數賦初值，并通過模擬試驗獲取級配碎石DTT 軸向應變的模擬值.

③比較步驟①與②中的實測值與模擬值，若軸向應變的誤差小于10%，即認為該組微力學參數為所需參數;否則調整參數，重新進行模擬試驗，直至誤差符合要求為止.

3 結論

1)基于PFC2D軟件，構建了級配碎石DTTNSM，研究了試驗條件對級配碎石動三軸試驗數值模擬結果的影響規律，并驗證了模擬方法的可靠性.結果表明:模擬試件在1 000 次動載作用下，塑性變形已趨于穩定;失穩偏壓隨圍壓增大而增大，提高圍壓能提高級配碎石抗變形能力;當試件尺寸為φ20 cm ×40 cm 時，可忽略試件的尺寸效應;動載作用時間和作用間隔時間分別取0.2 s 和2.0 s，與實際情況較吻合;級配碎石ε－N 曲線模擬值與實測值較吻合.

2)研究了微力學參數對級配碎石動三軸試驗數值模擬結果的影響規律，并提出了微力學參數標定方法.結果表明:級配碎石ε 與法向剛度kn、切向剛度ks、摩擦系數μ 均呈線性關系;建議摩擦系數μ 取值在0.5～1.0 之間.

References)

［1］李明國，牛曉霞，申愛琴.山區高速公路瀝青路面的抗車轍能力［J］.長安大學學報:自然科學版，2006，26(6):19－22.

Li Mingguo，Niu Xiaoxia，Shen Aiqin.Anti－rut ability of asphalt pavement on mountain freeway［J］.Journal of Chang′an University:Natural Science Edition，2006，26(6):19－22.(in Chinese)

［2］Gaskin P N，Raymond G P，Addo－Abedi F Y.Repeated compressive loading of a sand ［J］.Canadian Geotechnical Journal，1979，16:798－802.

［3］Werkmeister S，Numrich R，Dawson A R，et al.Deformation behavior of granular materials under repeated dynamic load ［J］.Environmental Geomechanics—Monte Verità，2002，2:1－9.

［4］Werkmeister S，Dawson A R，Wellner F.Permanent deformation behavior of granular materials［J］.Road Materials and Pavement Design，2005，6(1):31－51.

［5］何兆益.半剛性路面防止裂縫及其路用性能研究［D］.南京:東南大學交通學院，1997.

［6］廖化榮.紅黏土路基循環動載下塑性力學行為及預測模型研究［D］.廣州:中山大學地球科學系，2004.

［7］王龍，解曉光，巴恒靜.長期動載下級配碎石的塑性變形與臨界應力［J］.同濟大學學報:自然科學版，2010，38(9):1293－1297.Wang Long，Xie Xiaoguang，Ba Hengjing.Critical stress and plastic deformation of graded aggregate material under long－term dynamic repeat load［J］.Journal of Tongji University:Natural Science，2010，38(9):1293－1297.(in Chinese)

［8］金剛.級配碎石三軸試驗研究［D］.大連:大連理工大學土木工程學院，2007.

［9］李福普，嚴二虎.瀝青穩定碎石與級配碎石結構設計與施工技術應用指南［M］.北京:人民交通出版社，2009.

［10］蔣應軍，任皎龍，徐寅善，等.級配碎石力學性能的顆粒流數值模擬方法［J］.同濟大學學報:自然科學版，2011，39(5):699－704.

Jiang Yingjun，Ren Jiaolong，Xu Yinshan，et al.Simulation method of mechanical properties of graded broken stone based on particle flow code［J］.Journal of Tongji University:Natural Science，2011，39(5):699－704.(in Chinese)

［11］蔣應軍，李頔，馬慶偉，等.級配碎石力學性能影響因素的試驗研究［J］.交通科學與工程，2010，26(1):6－13.

Jiang Yingjun，Li Di，Ma Qingwei，et al.Experimental research on influencing factors of strength properties for graded broken stone［J］.Journal of Transport Science and Engineering，2010，26(1):6－13.(in Chinese)