有限元計算時拱橋樁基礎模擬方法

馮希訓，戴少雄，趙 欣

(天津市市政工程設計研究院，天津市300051)

0 引言

軟土地質區的大跨拱橋多采用樁基礎，有限元計算時，承臺以下樁基礎剛度取值大小對承臺底反力及上部結構內力的計算結果會產生影響。橋梁縱向剛度較大，如果在設計時不考慮樁基的柔度，有可能對上下部結構造成極大浪費，甚至導致設計計算錯誤。

下部結構的柔度主要體現在樁-土的相對剛度，即樁-土的相互作用，因此在設計計算時選擇合理正確的樁基礎模擬方法尤為重要。

1 4種常用樁基模擬方法

有限元計算時，群樁基礎的常用模擬方法一般有以下幾種：

(1)墩底固結法：即在拱座或承臺底完全剛性固結。

(2)假想嵌固點法：即在有限元模型中建出部分樁長固結。

此方法在港口工程樁基規范中有所介紹。對于嵌巖樁，如巖層面泥土的覆蓋層較薄，可假設樁嵌固點進入巖層一定深度。如巖層面泥土的覆蓋層較厚，則同摩擦樁一樣，彈性長樁的受彎嵌固點深度可用“m法”并按式(1)、(2)確定[1]：

式(1)、(2)中：t——受彎嵌固點距離提供樁側抗力的最上方土層的深度；

η——系數，取1.8～2.2，樁頂鉸接或樁的自由長度較大時取較小值，樁頂嵌固或樁的自由長度較小時取較大值；

T——樁的相對剛度系數，m；

Ep——樁材料彈性模量，kN/m2；

Ip——樁截面慣性矩，m4；

b0——樁的換算寬度(m)，b0取2d，d為樁受力面的樁寬或樁徑；

m——樁側地基土的水平抗力系數隨深度增長的比例系數，kN/m4。

(3)樁+等代土彈簧法：即將實際樁長建出，樁側用節點彈簧模擬出樁土間的水平作用剛度，但豎向剛度無法很好模擬。其水平剛度取值按式(3)確定：

式(3)中：ks——等代土彈簧水平剛度；

a——土層厚度，m；

bp——樁柱計算寬度(m)，可根據現行公路橋涵地基基礎規范確定[2]；

m——樁側地基土的水平抗力系數隨深度增長的比例系數，kN/m4;

z——計算深度，m。

(4)6自由度彈簧法：即下部樁基在模型中不建出，而在承臺底或墩底施加6自由度的彈簧剛度矩陣約束，剛度矩陣取值是由“m法”計算得出的樁頂的剛度值，橋梁設計計算時可參見現行《公路橋涵地基與基礎規范》(JTG D63-2007)[2]。

2 不同樁基模擬方法剛度對比

為對比4種樁基礎模擬方法對有限元計算結果的影響，以浙江臨海某橋位地質條件為背景，對4種方法的計算結果進行比較。其場地土層主要由粘土、淤泥、沙礫和圓礫等組成。順橋向設置3排樁基礎，每排橫向2根，樁徑3 m，縱橫向樁間距7 m，采用C30混凝土。統一取樁側地基土的水平抗力系數的比例系數m值為5 000 kN/m4(淤泥)、樁端m值50 000 kN/m4(圓礫)、內摩擦角20°進行建模計算。

其中，方法(2)假想嵌固點法計算深度t取13m；方法(3)樁+等代土彈簧法根據文獻[2]，縱、橫向水平剛度在同一節點取不同值，豎向約束剛度取方法(4)的豎向剛度平均分配到各樁頂；方法(4)6自由度彈簧法，采用“m法”計算樁頂剛度，對邊界施加6自由度彈性約束，結果如圖1所示。

圖1 計算用6自由度彈簧法剛度矩陣(單位：kN,kN·m)

利用橋梁專業軟件MIDAS/Civil7.4.1建立簡單剛架結構，將4種不同的樁基模擬方法施加于左立柱下方，在梁上分兩種工況施加相同的豎向、橫向集中荷載100 000 kN，如圖2(a)所示，模型采用邊界條件從左向右依次為墩底固結法、假想嵌固點法、樁+等代土彈簧法、6自由度彈簧法。在相同荷載工況作用下，4種方法的位移計算結果如圖2(b)、圖 2(c)、圖 2(d)所示。

圖2 相同結構同一地質條件用不同邊界模擬方法剛度對比

由圖2知，在相同荷載工況下，方法(3)“樁+等代土彈簧法”和方法(4)“6自由度彈簧法”縱向、橫向和豎向位移都十分接近，但前提是方法(3)的豎向約束剛度必須按方法(4)算得的豎向剛度平均分配到各樁頂來模擬，倘若方法(3)中直接在樁底固結或施加其它彈性約束，則總與方法(4)存在較大差異；方法(2)“假想嵌固點法”順橋向位移同方法(3)(4)一定程序上比較接近，但橫向、豎向剛度有差異稍大；方法(1)“墩底固結法”沒有模擬樁基柔度，其位移與其它3種方法在3個方向上差異均較大，可見樁基柔度對上部結構剛度影響較大，設計時若按墩底固結來處理可能導致設計不合理。

3 不同樁基模擬方法對拱橋受力的影響

為分析不同樁基模擬方法對拱橋受力的影響，將上節4種樁基邊界剛度參數完全移置到某拱橋承臺之下，計算其支反力和動力特性并進行對比。計算模型如圖3所示。

圖3 不同樁基模擬方法下某拱橋計算模型

拱橋最大的特點之一就是在豎向荷載作用下會產生水平推力，不同約束剛度下推力大小會有所不同，故分析同一地質條件下4種樁基模擬方法的承臺底反力，具有實際意義。在自重、系桿張拉力、升溫3種工況下，4種方法計算出的主拱承臺底反力如表1所列。

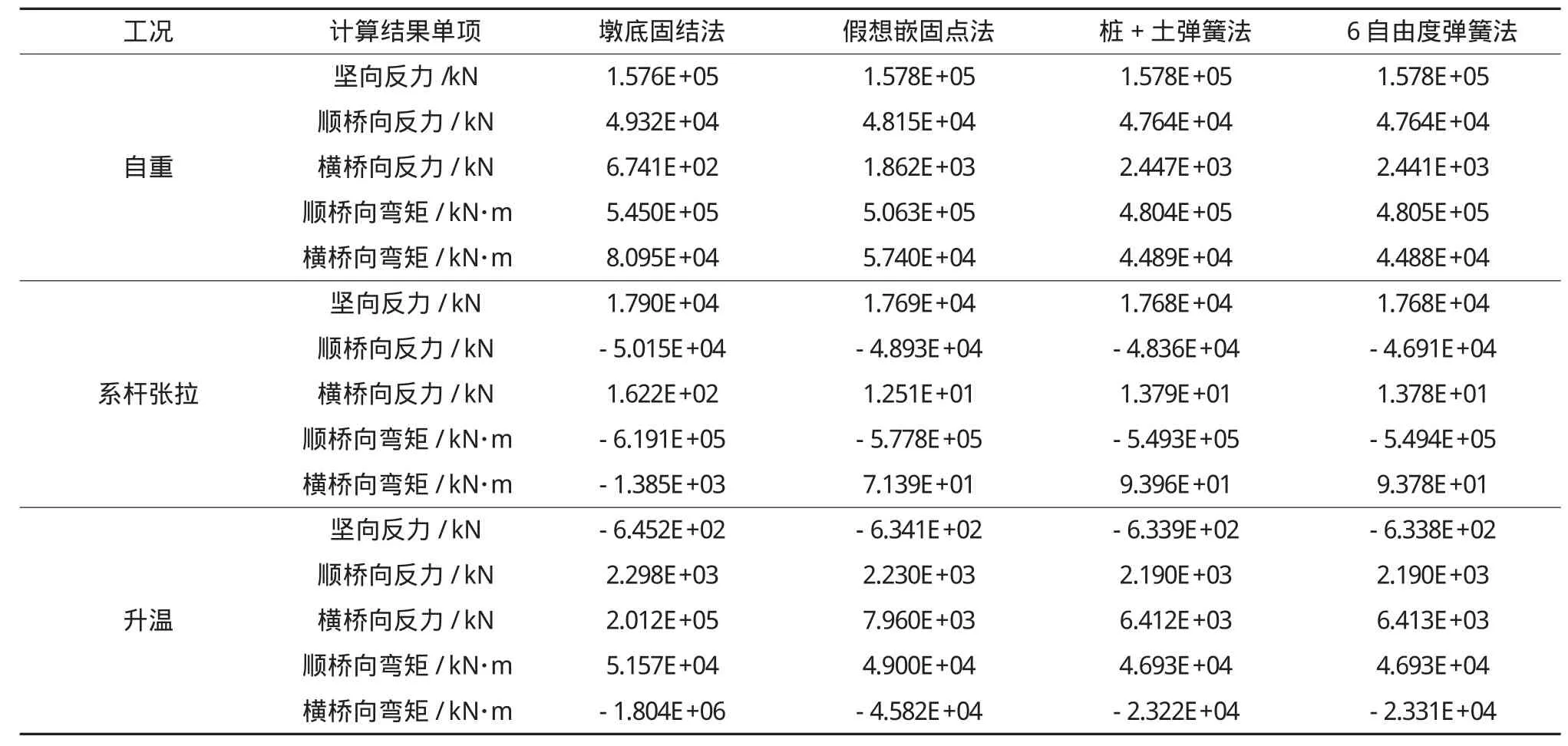
表1 樁基礎不同模擬方法對支反力的影響

由表1知，方法(3)“樁+等代土彈簧法”和方法(4)“6自由度彈簧法”在3種工況下承臺底反力十分接近，但前提也是方法(3)的豎向約束剛度必須按方法(4)算得的豎向剛度平均分配到各樁頂來模擬；方法(2)“假想嵌固點法”，豎向反力、順橋向彎矩和剪力與方法(3)、(4)比較接近，但橫橋向的彎矩、剪力相差稍大，可見當群樁基礎縱橫向數目設計不同時，此法不能很好地體現兩個方向的剛度差異；方法(1)“墩底固結法”沒有模擬樁基柔度，由于順橋向群樁剛度較橫橋向大，計算出的豎向反力、順橋向彎矩和剪力與方法(3)、(4)相差不多，而橫橋向彎矩、剪力相差很大，尤其是溫度作用下，其橫向剪力、彎矩已是方法(4)的31倍和77倍，而系桿張拉工況下橫向彎矩的符號已與方法(4)考慮樁土作用時相反。由此可見，在橋梁設計中當采用群樁基礎時需要考慮樁基柔度對上部結構的影響，且樁基越柔差異越大。

不同樁基模擬方法下，拱肋軸力、彎矩如表2所列，其中壓力以拱肋受壓為正，彎矩以使截面下緣受拉為正。

表2 不同樁基模擬方法對主拱肋內力的影響

由表2知，自重、升溫工況下，不同樁基模擬方法對拱肋軸力、彎矩影響不大；但水平系桿張拉力作用下，拱肋軸力相差較大，若不考慮樁基柔度直接在承臺底固結，則系桿拉力效應主要作用在邊界上，對拱肋軸力發揮作用很小，而計入實際樁基柔度后，拱肋軸力拉壓性質和大小都影響較大。可見對外部超靜定拱橋，靜力計算也應考慮樁基柔度作用。

不同樁基模擬方法下，各階振型頻率如表3所列。

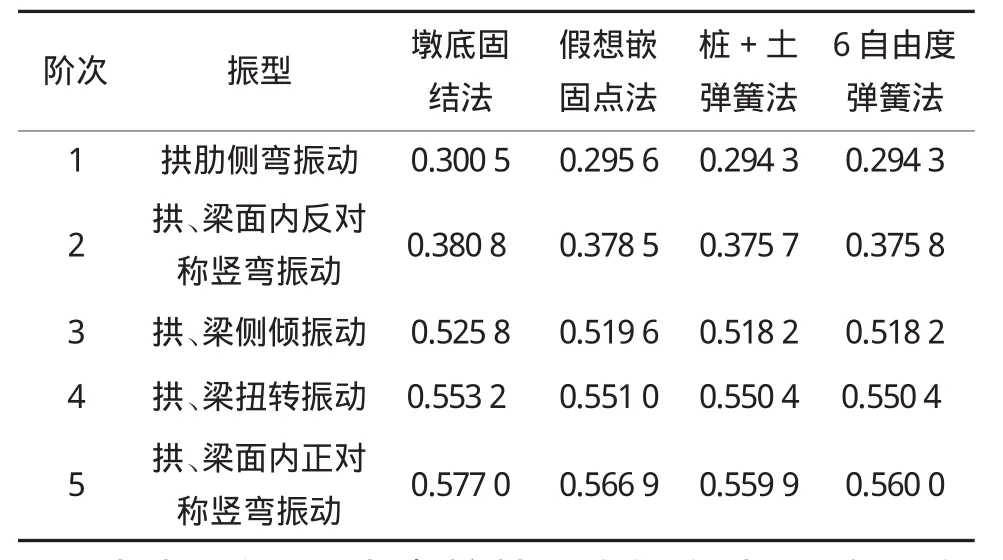
表3 不同樁基模擬方法下各階振型頻率(單位：Hz)

由表3知，不考慮樁基柔度的方法(1)在承臺底直接固結計算時，各階頻率比其它考慮樁基柔度的方法要大，過高地估計了結構的剛度；各階頻率方法(3)、(4)計算結果相近，方法(2)稍大。

4 結論

綜上所述，得出以下結論：

(1)對于外部超靜定的拱橋，用“墩底固結法”代替樁基邊界得到的下部結構反力與其他模擬方式(考慮樁土共同作用)結果相差很大，這將增加下部結構造價或導致設計不合理。水平系桿張拉力作用下，樁基柔度對拱肋軸力影響也較大。因此，在拱橋設計中需要考慮樁基柔度的影響。

(2)“6自由度彈簧法”是完全依據現行《公路橋涵地基與基礎設計規范》(JTG D63-2007)中“m法”，由不同地質條件和樁基幾何特性計算得出群樁的剛度(縱橫豎向彈性系數、縱橫向彎曲彈性系數、扭轉彈性系數及水平抗推剛度與繞水平軸抗彎剛度的耦合作用)，理論依據明確，較好地考慮了樁側、樁端土的作用，可視為基準方法，其它方法可與其比照來衡量計算的準確程度。

(3)“樁+土彈簧法”亦是依據“m法”計算出樁側土對樁的水平向約束剛度施加于樁側，通過對樁施加隨深度變化剛度的土彈簧單元來模擬不同方向的樁土聯合作用。依據規范《公路橋涵地基與基礎設計規范》(JTG D63-2007)，當群樁縱橫向數目不同時，樁基同一深度處縱橫向有不同的剛度系數；但其豎向剛度不好準確模擬，只有將“6自由度彈簧法”的豎向剛度平均分配到各樁頂時，兩種方法的計算結果才能較好吻合。

(4)“假想嵌固點法”是考慮樁土作用最簡單的方法，只需取一定樁長固結，但此種方法與“6自由度彈簧法”在平面外計算結果偏差稍大。

總之，對拱橋或其它外部超靜定結構橋梁，要準確模擬樁土作用最好使用“6自由度彈簧法”，若初步設計對計算精度要求不高時，也可采用“樁+土彈簧法”或“假想嵌固點法”。

[1]JTJ 254-98,港口工程樁基規范[S].

[2]JTG D63-2007,公路橋涵地基與基礎設計規范[S].

[3]周海林,冷伍明.樁基參數對單樁橫向剛度和橋墩自振頻率影響分析[J].四川建筑學研究，2001(3):38-43.