基于滑模變結構MARS的PMSM速度觀測器研究
潘文英,屈百達,徐保國
(江南大學輕工過程先進控制教育部重點實驗室,江蘇無錫214122)
永磁同步電機是交流伺服電機的一種,具有高轉矩慣性比、高能量密度、高效率等優(yōu)點,在航空、航天、電動汽車、工業(yè)控制領域獲得了越來越廣泛的應用。在伺服系統(tǒng)中,對速度的穩(wěn)定精度提出較高要求,能夠實行速度的閉環(huán)控制。因此速度檢測元件的正確選擇和構成速度負反饋控制的電路形式十分重要。高精度、高分辨率的速度傳感器(例如光電編碼器等)價格昂貴,不僅提高了伺服系統(tǒng)的成本,還限制了伺服驅動裝置在惡劣環(huán)境下的應用。運用無速度傳感器控制技術,通過各種速度觀測方法在線估計電動機的速度,從而省去傳感器,已成為一個研究熱點。
近年來,國內外學者就如何辨識電機的轉速做了大量的研究工作,提出了許多種方法,如直接計算法、模型參考自適應法(MARS)、擴展卡爾曼觀測器、轉子齒諧波法和高頻注入法等。文獻[1]采用了基于定子磁鏈矢量的參考模型和可調模型的MRAS方法。采用自適應算法調節(jié)上述兩種模型計算的定子磁鏈一致,進而觀測出電機轉速,該方法的精度依賴于電機參數(shù)的準確性。文獻[2]提出了一種高頻注入法的控制方法,通過給電機注入高頻電流,并檢測電機電流的響應值來獲取轉子的速度信息,但只適用于低速無速度控制,對于無凸極效應的面裝式PMSM控制效果不是很好。文獻[3]研究了擴展卡爾曼濾波器估算方法,盡管采用該方法能獲得較準確的轉子速度,但仍然存在模型復雜、計算量大等不足。
目前,模型參考自適應法以其算法不太復雜、抗干擾性能好、能保證參數(shù)估計的漸進收斂性、穩(wěn)態(tài)精度較高等優(yōu)點而頗受重視,已經(jīng)應用在無傳感器PMSM 矢量控制中。但只有解決高性能伺服系統(tǒng)中的參數(shù)變化、擾動等控制問題,才能進一步提高系統(tǒng)的控制性能。滑模控制不依賴于控制對象的數(shù)學模型,只按實際效果進行控制,在控制中有能力并可以充分考慮系統(tǒng)的不精確性和不確定性。文中提出了基于滑模控制的模型參考自適應控制速度觀測器的方法,仿真和實驗結果表明,所提出的控制方法具有較強的魯棒性和令人滿意的動靜態(tài)性能。
1 基于模型參考自適應控制速度觀測
1.1 永磁同步電機數(shù)學模型
三相永磁同步伺服電動機在dq坐標系下的數(shù)學模型:
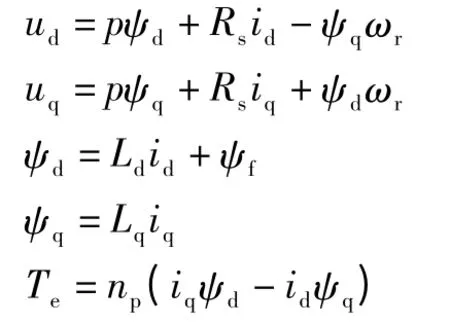
式中:ud、uq分別為d、q坐標系上的電樞電壓分量;id、iq分別為d、q坐標系上的電樞電流分量。
圖1為PMSM 無速度傳感器系統(tǒng)框圖。

圖1 無速度傳感器系統(tǒng)框圖
1.2 模型參考自適應控制方法
模型參考自適應法采用了基于定子磁鏈矢量的參考模型和可調模型的MRAS方法。如果由可調模型估計的定子磁鏈矢量與參考模型確定的ψs相同,那么轉速估計值一定與實際值ωr一致;如果兩者存在偏差,說明估計值與實際值ωr不符。顯然,轉速估計偏差與兩個模型估計的定子磁鏈矢量誤差間一定有必然的聯(lián)系,就是利用這個定子磁鏈矢量誤差構建一個合適的自適應律。調節(jié)上述兩種模型計算的定子磁鏈一致,使得可調模型的能逼近真實的ωr,進而觀測出電機轉速。
1.3 模型參考自適應法速度觀測器的實現(xiàn)
PMSM 在dq坐標系下得定子磁鏈數(shù)學模型
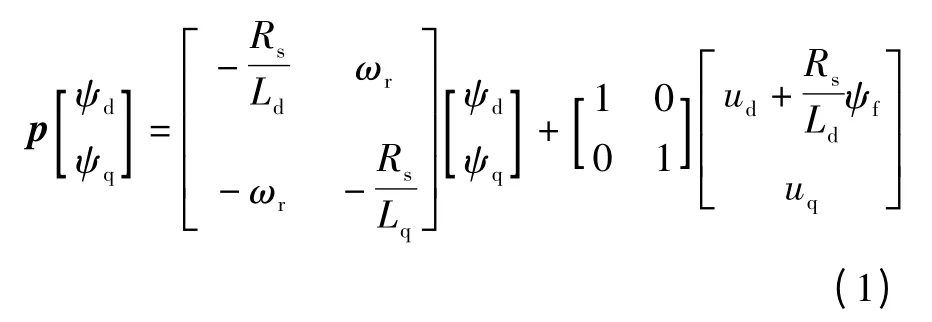
式中:ud、uq分別為定子電壓d、q軸的分量;Rs為定子電阻;Ld、Lq分別為d、q軸電感;ωr為轉速;ψf為轉子磁鏈;ψd、ψq分別為定子磁鏈d、q軸分量。式中包含有轉子速度,將其作為可調模型,ωr便是辨識的可調參數(shù)。
則構造參數(shù)可調的估算磁鏈模型為:

對應得:

線性時不變前饋系統(tǒng)G(S)=D(SI-Ae)-1為嚴格正實。
由popov 超穩(wěn)定理論,若這個反饋系統(tǒng)穩(wěn)定,其中非線性時變反饋環(huán)節(jié)必須滿足下述不等式:

當D=1時,V=e,對popov 積分不等式進行逆向求解,便可得到自適應律。

式中:
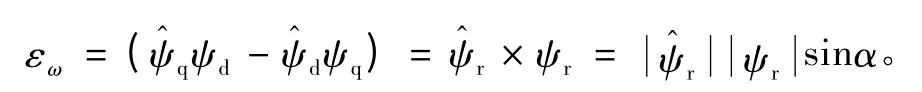
將得到的ψd、ψq作為參考模型:

將式(2)作為可調模型,式(4)作為參考模型,組成模型參考自適應速度觀測器如圖2所示。

圖2 模型PI 自適應速度器
2 基于滑模變結構自適應的速度觀測
2.1 滑模變結構控制方法
根據(jù)系統(tǒng)當前的狀態(tài)(如偏差及其各階導數(shù)等)有目的地不斷變化,迫使系統(tǒng)按照預定“滑動模態(tài)”的狀態(tài)軌跡運動,即為滑模變結構控制。這種變結構控制具有快速響應、對參數(shù)變化及擾動不靈敏、無需系統(tǒng)在線辨識、物理實現(xiàn)簡單等優(yōu)點。
2.2 滑模變結構自適應速度觀測器的實現(xiàn)
設計滑模變結構控制器的基本步驟包括兩個相當對立的部分:
(1)設計切換函數(shù)s(x),使它所確定的滑動模態(tài)漸近穩(wěn)定且具有良好動態(tài)性能。
滑動模態(tài)存在條件的成立是滑動模態(tài)控制應用的前提。如果系統(tǒng)的初始點x(0)不在s=0 附近,而是在狀態(tài)空間的任意位置,此時要求系統(tǒng)的運動必須趨向于切換面s=0。式(2)為滑模控制的狀態(tài)方程=f(x,u,t),設計切換函數(shù)
對切換函數(shù)求導得:

且當系統(tǒng)進入理想滑模狀態(tài)時,即當s·(x)=0時,獲得的為等效速度ωreq。
由式(5)得:

(2)設計滑動模態(tài)控制率u(x),使到達條件得到滿足,從而在切換面上形成滑動模態(tài)區(qū)。常規(guī)滑模變結構控制的設計方法有常值切換控制、函數(shù)切換控制、比例切換控制。根據(jù)控制要求選用常值切換控制u=u0sgn(s(x)),其中,u0是待求的常數(shù),sgn是符號函數(shù)。
一旦切換函數(shù)s(x)和滑模控制律u(x)都得到了,滑模變結構控制就建立起來。即=k·的低頻分量為等效速度。
2.3 滑模變結構控制抖振問題
滑模變結構控制在本質上的不連續(xù)開關特性將會引起系統(tǒng)的抖振,抖振會影響控制的精確性,增加能量消耗,破壞系統(tǒng)的性能。可在滑動模態(tài)控制中引入準滑動模態(tài),采用Sigmoid 連續(xù)函數(shù)代替切換函數(shù),較傳統(tǒng)滑模速度觀測器減少了濾波環(huán)節(jié)和相位補償環(huán)節(jié)。
滑模變結構自適應速度觀測器(圖3)轉速估計為:

式中:H為Sigmoid函數(shù),用連續(xù)函數(shù)代替切換函數(shù)。

式中:a為大于零的實數(shù),根據(jù)實際情況而定。

圖3 滑模變結構自適應速度器
將基于模型參考PI 自適應無速度傳感器的速度觀測器與基于滑模控制的模型參考自適應無速度傳感器速度觀測器系統(tǒng)進行比較。
初始給定轉速為2 000 r/min,在t=0.1 s時加入4 N·m的負載轉矩,圖4為突加擾動時的實際和估計轉速。
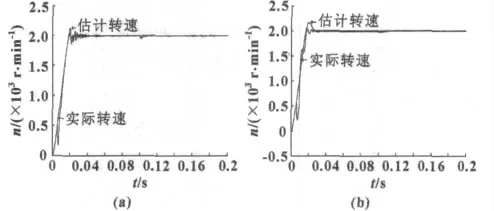
圖4 突加擾動時的實際和估計轉速曲線
圖4(a)為PMSM 實際轉速輸出與基于模型參考PI 自適應速度觀測器的轉速輸出對比圖,可以看出:估計轉速輸出與實際速度變化曲線幾乎一致,t=0.04 s時趨向于穩(wěn)定,且突加擾動時速度發(fā)生很小變化后穩(wěn)定到給定值。圖4(b)為PMSM 實際轉速輸出與基于滑模控制的模型參考自適應速度觀測器的轉速輸出對比圖,可以看出:加入滑模控制的速度曲線波動較小,更平穩(wěn),且于t=0.03 s時就趨向于穩(wěn)定,突加負載擾動時速度變化更小。
當初始給定轉速為2 000 r/min,在t=0.1 s給定轉速變化為1 500 r/min,圖5為此刻轉速變換時的實際和估計轉速。當速度發(fā)生突變時,速度觀測器的估計轉速動態(tài)響應快,跟蹤性能好。圖5(b)中加入滑模控制的速度觀測器較圖5(a)的模型PI 自適應速度觀測器其穩(wěn)態(tài)轉速動態(tài)響應更快,更平穩(wěn),跟蹤性能更好。從圖6可以看出所提出的無速度傳感器速度觀測估計位置和實際位置幾乎一致。由以上的仿真分析可以看出:無速度傳感器的估計轉速與實際轉速非常接近,除了電機在剛啟動時有較大誤差,待系統(tǒng)穩(wěn)定后,估計轉速與實際轉速趨向一致,達到很好的控制效果。而基于滑模控制的模型參考自適應無速度傳感器具有更好的性能。

圖5 轉速變化時的實際和估計轉速曲線

圖6 實際位置和估計位置曲線
3 結論
采用無速度傳感器辨識方法代替速度傳感器來對永磁同步伺服電機進行速度辨識。通過對基于模型參考自適應控制的速度觀測器和基于滑模控制的模型參考自適應控制的速度觀測器方法進行仿真研究,可知后者能夠更好地檢測轉子實際速度和位置,是性能更好的速度辨識方法,為交流伺服系統(tǒng)提出了一種很好的控制方法。
【1】秦峰,賀益康,賈洪平.基于轉子位置自檢測復合方法的永磁同步電機無傳感器運行研究[J].中國電機工程學報,2007,27(3):12-17.
【2】王慶龍,張崇巍,張興.交流電機無速度傳感器矢量控制系統(tǒng)變結構模型參考自適應轉速辨識[J].中國電機工程學報,2007,27(15):70-74.
【3】聶建華,燕婧婧.基于自適應EKF的PMSM 無速度傳感器控制[J].電氣傳動,2011,41(3):16-18.
【4】樊立萍,楊林.電氣伺服系統(tǒng)的自適應模糊積分滑模控制[J].電力系統(tǒng)及其自動化學報,2010,22(2):27-31.
【5】VACLAVEK P,BLAHA P.Lyapunov Function-based Flux and Speed Observer for AC Induction Motor Sensorless Control and Parameters Estimation[J].IEEE Trans Ind Electron,2006,53(1):138-145.
【6】HAN Y S,CHOI J S,KIM Y S.Sensorless PMSM Drive with a Sliding Mode Control Based Adaptive Speed and Stator Resistance Estimator[J].IEEE Trans on Magnetics,2000,36(5):3588-3591.
【7】劉金錕.滑模變結構控制Matlab仿真[M].北京:清華大學出版社,2005.

